基于信道脉冲响应物理密钥的随机性分析*
2019-09-04肖方恒
肖方恒,石 会,龚 晶
(陆军工程大学 通信工程学院,江苏 南京 210007)
0 引 言
无线信道的开放性给人们的通信安全带来巨大的威胁,通信安全是移动无线通信中必须要解决的一个核心问题。随着计算机运行速度的不断提升,传统加密手段已难以满足通信安全。近些年来,基于信息论的物理层安全技术成为解决无线通信安全的新方法。其中,基于信道脉冲响应CIR(Channel Impulse Response,CIR)方案生成的物理密钥具有生成速率较高、一致性好等优点[1]。而物理密钥的随机性好是保证信息安全的前提和基础,随机性检验可以检测生成物理密钥流是否符合随机性要求。随机性检验有多种方法,本文采用通用的局部随机性检验方法,即最常用的五种随机性检验方法,分别为:频数检验、序偶检验、游程检验、扑克检验和自相关检验。因此,本文主要分析基于CIR生成物理密钥的随机性能。
1 局部随机性检验
基于安全性角度,密钥流的特性最好是真随机的,真随机序列具有统计的随机性、不可预测性和不可再生性。但实际密码系统中使用的密钥流序列都是伪随机序列,即满足伪随机序列应该具备的统计特性:平衡特性、游程特性与自相关特性,即认为密钥流是随机的[2]。从安全性角度考虑,密钥流的周期通常很长,而每次通信时仅使用其中很短的一段密钥,因此密钥流中的局部也要求具有很好的随机性,即需要对密钥流进行局部随机性检验。本文选取的是最常用的五种局部随机性检验方法,分别是:频数检验、序列检验、扑克检验、自相关检验和游程检验。当密钥流能全部通过这五种随机性检验,即认为密钥流是随机的。
1.1 测试的相关统计学概念
本文中的测试方法主要涉及到两类统计学中的基本分布,下面对测试方法所涉及的相关统计学知识做简单介绍[2]:
1.1.1 正态分布
若随机变量X的概率密度函数(probability density function,pdf)为:

其中,μ,σ为常数,且σ>0,则称X服从参数为μ,σ的正态分布,记为X~(μ,σ2)当参数为 (0,1)的正态分布则称为标准正态分布。
1.1.2 χ2分布
设随机变量X1,X2,…,Xn服从标准正态分布,且相互独立,则称统计量服从自由度为n的χ2分布。χ2分布的概率密度函数pdf为:

其中,x≥0。
1.2 随机性分析方法
1.2.1 频数检验
频数检验是为了考察一个密钥流序列中0和1的平衡性。设一个长度为n的被检测密钥流序列中有n0个0和n1个1,根据式:

计算x2的值,与χ2分布表中对应的门限值)(其中α表示χ2分布的显著性水平,v表示χ2分布的自由度)进行比较,这里v=1;当x2<χα2(v)时,表示该密钥流序列通过频数检验。
1.2.2 序偶检验
序偶检验用来考察一个密钥流序列是否具有合适的转移概率,即两个相邻元素间的不同组合出现次数是否大致相同。设一个长度为n的被检测密钥流序列中组合00、01、10和11出现的次数分别为n00、n01、n10和n11,0和1出现的次数分别为n0和n1,根据式:

计算x2的值,并和χ2分布表中对应的门限值进行比较,这里v=2;当时,表示该密钥流序列通过序偶检验。
1.2.3 扑克检验
将一个n比特密钥流按m比特为单位分组后,扑克检验用来考察各种组合出现的频次是否近似相等。假设各分组中自然数i(0≤i≤2m-1)出现的次数为ni,根据式(5):

计算x2的值,其中将x2和χ2分布表中对应的门限值χα2(v)进行比较,这里v=2m-1。当x2<χα2(v)时,表示该密钥流序列通过扑克检验。(扑克检验的自由度为v=2m-1,m是分组长度)。
1.2.4 自相关检验
将一个长度为n比特的密钥流序列经移位变换后与原序列之间的相关性,用自相关检验来考察。设序列s经d位移位变换后的序列与原序列对应位置上信号不同的个数为c(d),根据式(6)计算C的值:
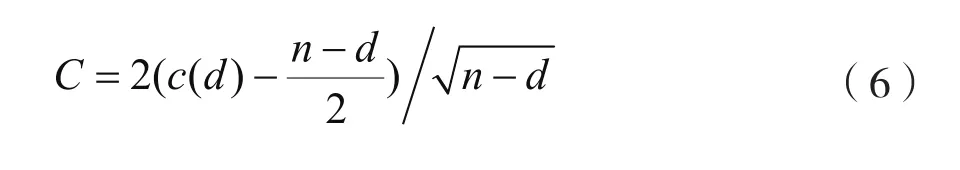
双边分位数的计算方法是:计算1-α/2的值,在正态分布表中查找该值,该值所对应的最左侧第一列值与第一行值的和为双边分位数,即在显著性水平α下的门限值[3]。
1.2.5 游程检验
游程检验是用来考察一个长度为n比特的密钥流序列中0和1的分布是否合理。设长为i的0游程的个数为Bi,长为i的1游程的个数为Gi,Bi和Gi的数学期望为ei,根据公式(7)计算x2的值:

其中,ei=(n-i+3)/2i+2,k为使ei≥5的最大整数。将x2与χ2分布表中对应的门限值χα2(v)进行比较,这里v=2k-2;当x2<χα2(v)时,表示该密钥流序列通过游程检验。(游程检验的自由度为v=2k-2)。
2 物理密钥生成与随机性分析
本文运用MATLAB软件仿真分析基于信道脉冲响应生成物理密钥的随机性,具体仿真流程如图1所示。

图1 MATLAB仿真流程
首先,合法的通信双方Alice和Bob基于信道脉冲响应生成初始物理密钥Key_A和Key_B;其次,采用Cascade协商算法[4]对密钥Key_A和Key_B进行一致性协商,以得到完全一致的物理密钥;最后,对物理密钥进行随机性分析即频数检测、序偶检测、扑克检测、自相关检测和游程检测。
2.1 物理密钥生成
物理密钥的具体生成过程可分为3个阶段[5]:首先,构造瑞利衰落信道的Jakes模型[6],其中多径数目N=50,载波频率ωc=2*10-9rad/s,采样频率fs=20 Hz,最大多普勒相移ωm=2*πrad/s。本文选取瑞利衰落信道的同相分量作为CIR的理论值,将其叠加上信噪比为30 dB高斯白噪声后作为CIR的估计值;然后,合法通信双方分别对CIR估计值进行多比特自适应量化(Multi-bit Adaptive Quantization,MAQ)、编码,分别得到初始物理密钥Key_A、Key_B;最后,采用Cascade密钥协商算法以得到完全一致的物理密钥。经过MAQ量化、编码和Cascade协商后,每次随机仿真产生了2 000比特一致的物理密钥,经过15次随机仿真可得到30 000 bit完全一致的物理密钥。考虑到实际系统中密钥加密长度,本文中选取分组为256比特物理密钥进行随机性分析。从30 000 bit物理密钥中选取前25 600 bit,可得到100组、每组256 bit的一致物理密钥流,然后分析这100组物理密钥流的随机性。前10组、每组256 bit物理密钥流如表1所示。

表1 前10组、每组256比特的一致物理密钥流
2.2 随机性分析
在MATLAB仿真程序中,对100组、每组256 bit的物理密钥流进行五种随机性测试,前10组、每组256 bit物理密钥流的五种随机性检测指标如表2所示。

表2 前10组物理密钥流随机性检测结果
从表2中可以看出:第7、9组物理密钥流未通过频数检测,第7、9、10组物理密钥流未通过序偶检测。
在进行的100组物理密钥的五种随机性测试中,未通过随机性测试的组号如表3所示。

表3 100组物理密钥流未通过随机性检测组号
由表3可以看出,在100组物理密钥中,未通过频数检测共21组,未通过序偶检测共19组,4组物理密钥未通过扑克检测,5组物理密钥未通过自相关检测,1组物理密钥未通过游程检测;频数检测和序偶检测的通过率比较低;共计71组物理密钥均通过五种随机性检测。由此可知,基于CIR的物理密钥随机性能较好。
3 结 语
本文介绍了常用的五种随机性测试方法,利用MATLAB软件生成了基于信道脉冲响应CIR的物理密钥,经过量化,编码和协商后,得到完全一致的物理密钥,并将一致的物理密钥分成100组,每组256 bit,对这100组物理密钥进行五种随机性测试,随机性测试表明,100组物理密钥中,有71组物理密钥能全部通过五种随机性测试,即通过率为71%,说明基于CIR信道脉冲响应生成物理密钥的随机性较好。
