基于flocking的多智能体群集与避障算法研究与仿真*
2019-09-04朱永川何健辉
刘 婵,朱永川,白 园,何健辉
(中国电子科技集团公司第三十研究所,四川 成都 610041)
0 引 言
随着人工智能和智能体技术的发展和社会需求的进一步提高,多智能体技术研究成为热点问题。多智能体系统不是单个智能体的简单堆砌,而是多个智能体的协同组合,不仅有效地避免了单个智能体的不足,同时充分发挥了智能体群体的优势。与单智能体相比,多智能体系统具有适合完成复杂任务、功能分布化、体系生存率、高效费比等优势。多智能体系统可以应用于星球探索、海洋勘探、无人机群、无人艇群、无人坦克群等领域,且能产生巨大的效益[1-2]。
多智能体运动规划问题逐渐成为智能体中研究的热点问题。多智能体运动规划主要包括路径规划、编队控制和避障避碰三种控制行为。1986年,Reynolds最早提出了模仿动物聚集行为的计算机模型,由三条基本规则构成,即聚集(Flock Centering)、结对(Velocity Matching)、避撞(Collision Avoidance)[2]。2006年 R. Olfati-Saber提 出 基 于flocking的多智能体动态系统理论及算法,并提出了三种群集算法:(1)不存在目标时的群集算法;(2)存在追踪目标时的群集算法;(3)多障碍情况下的群集算法[3]。在此之后,许多学者对flocking算法进行了研究,包括该算法碰撞避免算法、离散时间算法、参数设置与优化等[4-7]。
本文主要介绍了基于分布式flocking的群集控制模式,根据Reynolds提出的三条规则,以及人工势场群集算法,实现了多智能体系统的集结与共识,使多智能体在运动过程中保持一致性,并为系统提供冗余性和结构的灵活性;同时对多智能体的避障控制和目标点控制开展了进一步的研究,解决群集避障问题,使得群体能够平滑地绕过静动态障碍物,在复杂环境下成功抵达任务目标区域;最后仿真结果显示多智能体能集结,并达成共识,最终越过障碍物抵达目标节点,验证了该算法的合理性和有效性。
1 多智能体群集与避障算法研究
采用分散控制的策略,将多智能体群体运动的总控制律分成三个子控制律,即编队控制、避障控制、目标控制,分别研究了多智能体运动中智能体之间位置和速度的协调、躲避障碍物和向目标点移动的控制,如图1所示。
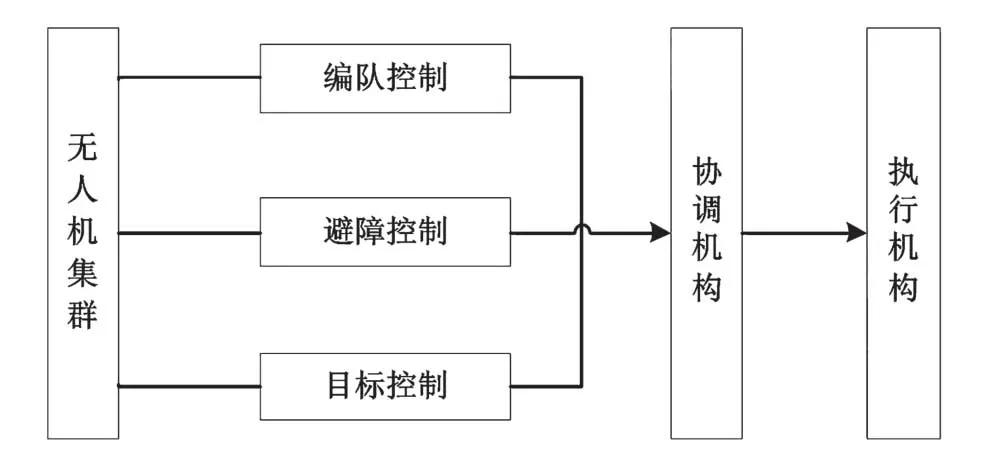
图1 智能体集群运动模型
1.1 多智能体群集运动基本模型
根据图1所示的多智能体运动模型,假设第i个α-智能体的控制律为μi,则

式中,μiα为编队控制律,μiβ为避障控制律,μiγ为目标点移动控制律,第i个α-智能体的控制示意图如图2所示。其中三角形区域为α-智能体的目标区域,rβ为α-智能体的感知距离,dβ为β-智能体的影响距离,rα为α-智能体的通信距离,dα为α-智能体的安全距离,α-智能体的属性为[pi,vi],β- 智能体的属性为 [p^i,k,v^i,k],μi1α和μi2α为第i个α-智能体的编队控制律,μiβ为第i个α-智能体的避障控制律,μiγ为第i个α-智能体的目标点控制律。
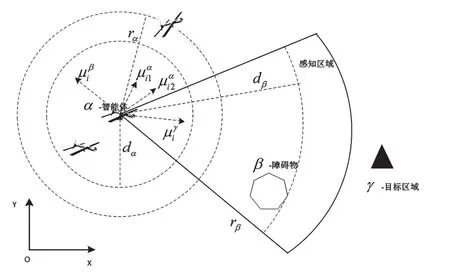
图2 第i个α-智能体的控制示意图
1.2 多智能体群集控制与共识算法研究
考虑由N个α-智能体组成的智能群体,其动态方程为:
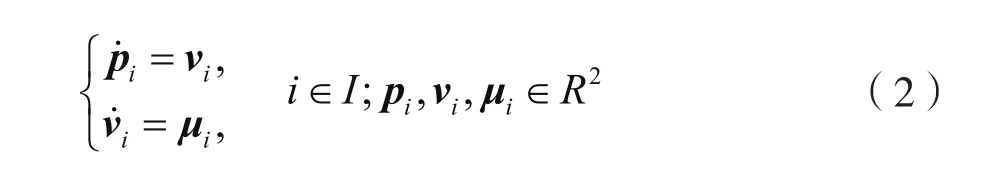
第i个α-智能体的邻接节点集合用Ni表示,则定义:

α-智能体的邻接矩阵用A=[aij]表示,其中对于否则,aij=0。
为了构建群集运动的一个光滑集成势场以及构建一个邻接网络的空间邻接矩阵,定义一个叫做σ范式的非负地图。

并用冲击函数来构建光滑势场函数以及光滑邻接矩阵,选择冲击函数如下:

其中,h∈(0,1)。用这个冲击函数,可以定义空间邻接矩阵A(p):
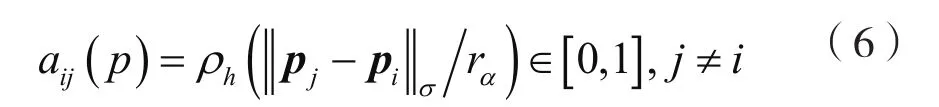
当第i个α-智能体与邻接节点保持距离dα时,认为其几何结构处于稳定状态,即
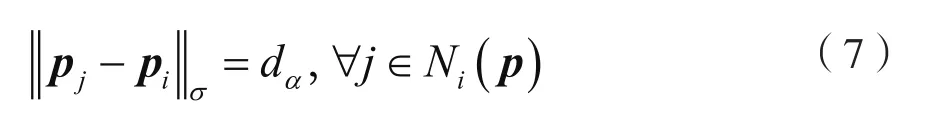
α-智能体群体之间根据Reynolds提出的聚集行为三条基本规则,避撞、结对、聚集,构建一个光滑的成对势场,描述了任意两个α-智能体之间内部的运动规则。
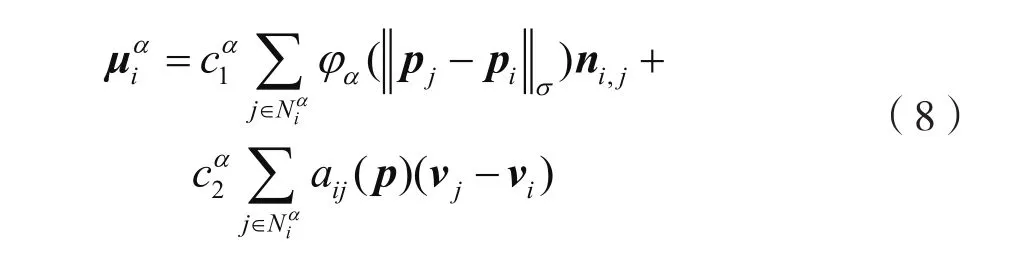
其中,
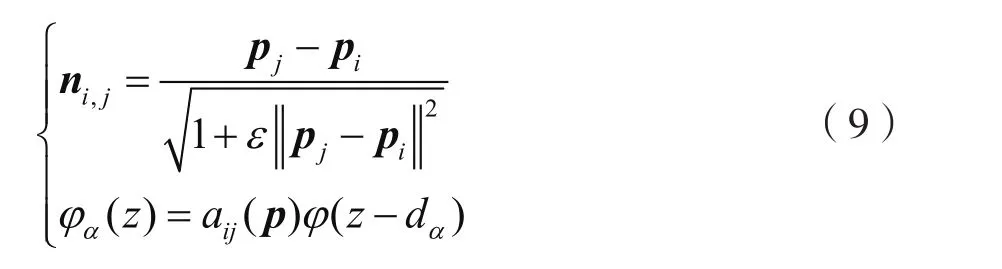
其中,
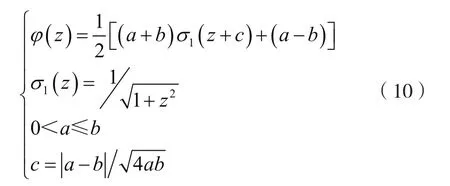
当α-智能体群体根据该算法进行群集控制时,需要判定该群体是否达成了共识。我们可以参考Reynolds提出的聚集行为基本规则,获得智能体群体共识条件:
(1)根据邻接矩阵,利用连通图检测网络连通情况,若连通最大分量为M,则需M=N;

(4)存在k0∈N,对于所有的k≥k0和所有的i∈I,maxj∈I{i}||pj(k)-pi(k)||≤dc,其中dc为智能体之间的最大距离;
(5)存在k0∈N,对于所有的k≥k0和所有的i∈I,minj∈I{i}||pj(k)-pi(k)||≈dα,其中dα为智能体之间的安全距离。
当多智能体达到以上条件时,认为该群体已达成共识。
1.3 多智能体群集避障控制算法研究
对于中心位置位于pk,半径为Rk的β-智能体障碍物Ok,dβ为该智能体的影响距离。表示第k个β-智能体的位置表示第k个β-智能体的速度向量。假设,场景内共有k个β-智能体障碍物,第i个α-智能体能够感应到的β-智能体障碍物集合用表示,则定义:
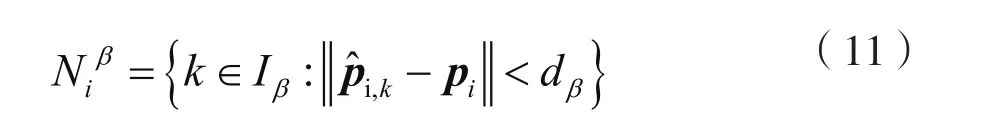
其中,Iβ={1,2,…,K}
相对第i个α-智能体,对于β-智能体障碍物的位置和速度可由下式确定:

式中,
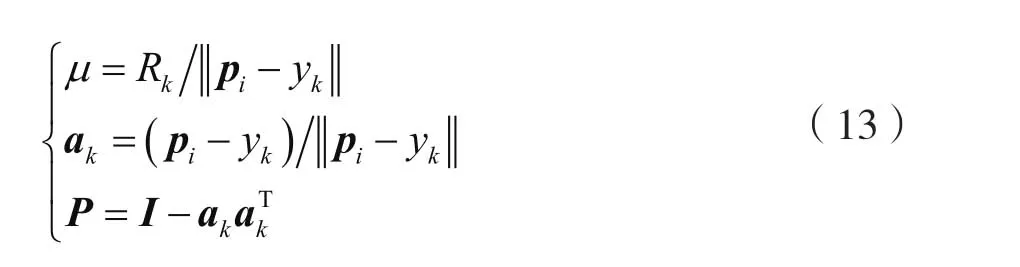
其中,I为单位矩阵。
定义影响矩阵B(p):
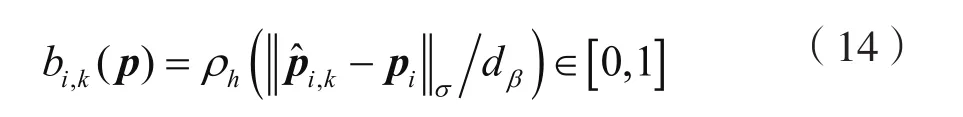
针对第i个α-智能体,与β-智能体障碍物的斥力关系如下:
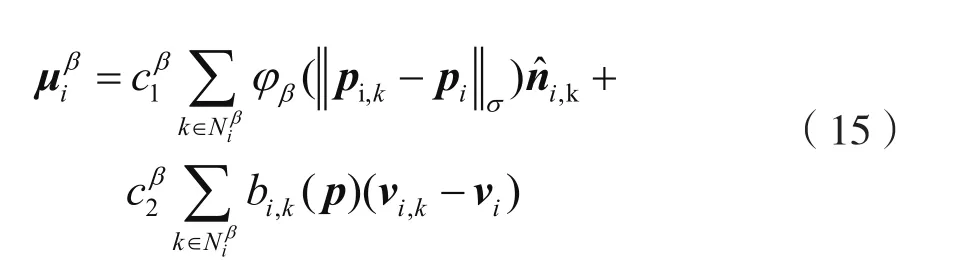
其中,
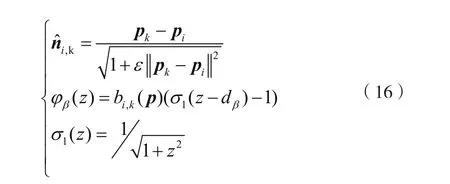
式中,c1β,c2β为加权系数。
1.4 目标点控制器设计
根据人工势场的特点,综合考虑位置矢量和速度矢量带来的影响,针对第i个α-智能体,设计目标点控制律为:
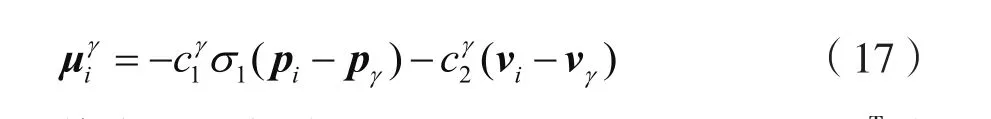
其中,目标点γ的属性为表示γ目标点的位置矢量表示γ目标点的速度矢量为加权系数。
2 多智能体群集与避障算法仿真
本节主要是通过MATLAB仿真实现基于flocking的多智能体群集控制与共识、避障控制,以及任务目标区域抵达的功能。该算法的参数设置比较关键,在此,设置参数dα=22.5,rα=1.2dα;dβ=56.25,rβ=2.5dβ;ε=0.2;Ts=0.05。
2.1 多智能体群集控制与共识算法仿真
假设α-智能体群体个数为50,在[-200 m,200 m]范围内进行多智能体位置随机初始化,在[-2 m/s,2 m/s]范围内进行智能体速度随机初始化。则在不同时刻,α-智能体群体的仿真变化如图3所示。


图3 50个α-智能体群体控制与共识算法仿真
如图3所示,图3(a)表示t0时刻,50个α-智能体群体随机分布的初始位置;图3(b)表示t1时刻,已有一小部分团体达成共识;图3(c)表示t2时刻,已有大部分智能体达成共识;图3(d)表示50个α-智能体群体已达成共识,组成分布式集群。
随机分布的多智能体达成共识,构成智能体群集,智能体之间的相干性如下式所示,

其中,N表示智能体数量,ψscal(t)表示智能体之间的相干性,当ψscal(t)≈1时,表示在理想的集群状态;当ψscal(t)≈0时,在无序状态或者智能体群集悬停状态。
每一时刻智能体之间的相干性变化曲线图如图4所示。曲线很快趋于1附近波动,说明50个智能体的速度趋于一致性。
2.2 多智能体群集避障控制与目标区域抵达功能测试
假设50个已达成共识的多智能体群集在设定场景下进行避障功能和目标区域抵达功能测试,测试结果如图5所示。

图4 相干性变化曲线图


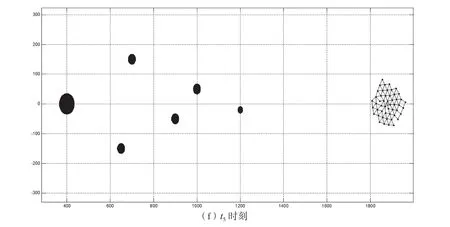
图5 多智能体群集避障控制与目标区域抵达功能测试
如图5所示,图5(a)表示t0时刻,50架智能体集群的初始位置,以及障碍物的分布情况;图5(b)-(e)表示t1-t4时刻,智能体根据当前态势顺利绕过障碍物,继续往目标点飞行;图5(f)表示t5时刻,智能体绕过障碍物之后,都朝目标点飞行,最终又达成共识,组成集群,并成功抵达任务目标区域。
3 结 语
本文主要介绍了基于分布式flocking的群集控制模式,根据多智能体之间的分离性、队列性和凝聚性,实现了多智能体系统的集结与共识,并对多智能体的避障控制和目标点控制开展了进一步的研究,最后通过仿真验证了该算法的合理性和有效性,对多智能体群集运动研究具有重要的理论指导意义。
