关于拉格朗日乘数法的两点札记

山西省临汾市第三中学(041000) 浙江省宁波市北仑明港中学 (315806)

张荣华 甘大旺

文[1]中介绍多元函数在已知条件下求极值的拉格朗日乘数法，文[2]介绍二元函数在已知条件下求极值的待定系数乘数法.前者运用偏导数，属于高中生灵活运用导数的一个最近发展区；后者运用初等方法，也有探究趣味.本文双向延伸[1]的思路，给出了拉格朗日乘数法的两点札记，供参考.

札记1泛化运用拉格朗日乘数法求多元函数的最值，条件等式可能不止一个.

例1 (2015年全国联赛题)若实数a、b、c满足2a+4b=2c，4a+2b=4c，求c的最小值.

解：设x=2a、y=2b、z=2c，则得到两个条件等式x+y2=z、x2+y=z2.

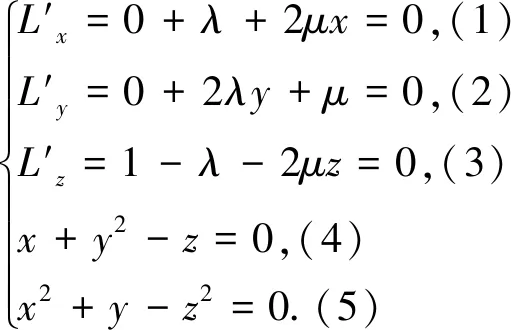
由(1)(2)得u(4xy-1)=0(6)，

由(1)(3)得2u(x-z)=-1≠0(7).

则由(6)(7)得4xy=1≠0(8).

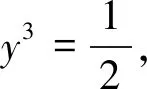
训练题1.1 (2018年吉林省竞赛题改编题)已知正实数x、y、z满足x+y=xy，且x+y+z=xyz，求z的最大值.

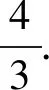
训练题1.2 (第60届捷克和斯洛伐克决赛题)已知实数x、y、z满足x+y+z=12，且x2+y2+z2=54，求证：xy、yz、zx均在[9,25]的范围内.

提示：先取拉格朗日函数L(x,y,z)=xy+λ(x+y+z-12)+μ(x2+y2+z2-54)，可求9≤xy≤25.同理得，9≤yz≤25，9≤zx≤25.

札记2退化运用拉格朗日乘数法求多元函数的最值，条件等式可能不存在.

例2 (2009年中国科大自主招生题)求证：∀x、y∈R，x2+y2+xy≥3(x+y-1)恒成立.

于是(1,1)是二元函数f(x,y)的唯一极值点.又因为f(1,1)=0

注释：在此例解题过程中，设想增加一个恒成立条件等式1=1，并设想拉格朗日函数L(x,y)=x2+y2+xy-3(x+y-1)+λ(1-1)，从而可以理解此例的解题思路实质上是贯通运用了拉格朗日乘数法的退化形式.

训练题2.1 (2017年清华大学标准学术能力测模拟试题,正确选项不一定唯一)设x、y∈R，函数f(x，y)=x2-2xy+6y2-14x-6y+72的值域为M，则( ).

A.1∈MB．2∈MC．3∈MD．4∈M

提示：可求二元函数f(x,y)的有唯一极值点(9,2)，再不妨取点(0,0)，验算得f(9,2)=3<72=f(0,0)，于是f(x,y)的值域M=[3,+∞)，所以选C、D.

最后指出，把拉格朗日乘数法及其泛化、退化形式纳入高中数学的校本选修教材之中是可教、易学、有用的！