一道高三质检题的探究*

福建省莆田第二中学 (351131)

蔡海涛

1.试题呈现

(1)求函数f(x)的单调区间；

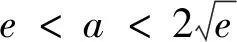
2.试题分析

题目结构比较简单,以含对数函数及分式函数的初等函数为载体，与不等式相结合.试题分步设问,逐步推进,由浅及深,较好地达到了考查目的.第一问考查的是导数的应用,利用导数求函数的单调区间基础知识,考查运算求解能力,考查函数与方程思想、分类与整合思想等；第二问考查的是利用导数研究函数的最值、零点，证明不等式等基础知识,考查抽象概括能力、推理论证能力,考查化归与转化思想、函数与方程思想、分类与整合思想等.

3.解法赏析

试题的第二问涉及双参数问题的证明，方法较多，下例举几种常用方法，旨在抛砖引玉.

当x>1时，g′(x)<0，函数g(x)在区间(1,+∞)上单调递减.所以g(x)在x=1处取得最大值.

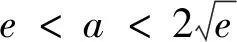
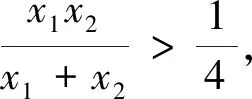
评注:本法思路与证法1类似,把x1+x2用x1x2来替换,区别之处是构造的函数中还有a这个参数,因此得到构造函数的最值也含有a,要通过放缩进行转化.

评注:本法思路以双参数中一个参数x1为主元,构造以x1为变量的函数.在构造函数中,主元的确定很重要,本题也可构造成以x2为变量的函数,方法类似,本文不再赘述.

4.试题变式

(1)求a的取值范围；(2)求证：x1+x2>2e.

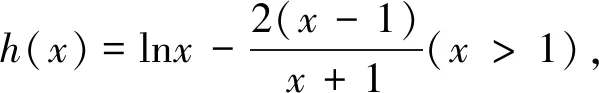
5.解后反思

在高考中,函数与导数问题一般含有参数,如果是双参数问题,一般是想方设法把双元先通过换元或其它方法,转化为一个变量问题,再进行求解.本文所提供的几种变形方法本质都是转化为一个变量函数问题.