一道韩国数学奥林匹克题的新解及推广*

陕西安康学院数学与统计学院 (725000)

赵临龙

考题[1](第19届韩国数学奥林匹克竞赛题)在△ABC中,∠B≠∠C,△ABC的内切圆⊙O与BC、CA、AB的切点分别为D、E、F.记AD与⊙O的不同于点D的交点为P.过点P作AD的垂线交EF于点Q,X、Y分别是AQ与直线DE、DF的交点.求证:

A是线段的中点.

本刊先后在文[2-3]中，介绍到有关射影几何知识，我们可以用这些知识来研究竞赛题，给出新的证明方法，并将竞赛题进行推广.

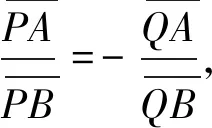
特例当点P为中点，则点Q为无穷远点；反之，也成立.

引理1[4]如图1.完全四边形ABCD的两对角线AB、CD交于点P，且AB、CD分别交对角线MN于Q、R，则点A、B调和分割P、Q.

推论1 当AB平行NM时，则P为AB的中点.

引理2[3]过点P(x0，y0)引二次曲线Γ：ax2+2bxy+cy2+2dx+2ey+f=0的两切线PE，PF切Γ于E、F两点，则切点弦EF的方程为l：ax0x+b(y0x+x0y)+cy0y+d(x0+x)+e(y0+y)+f=0.

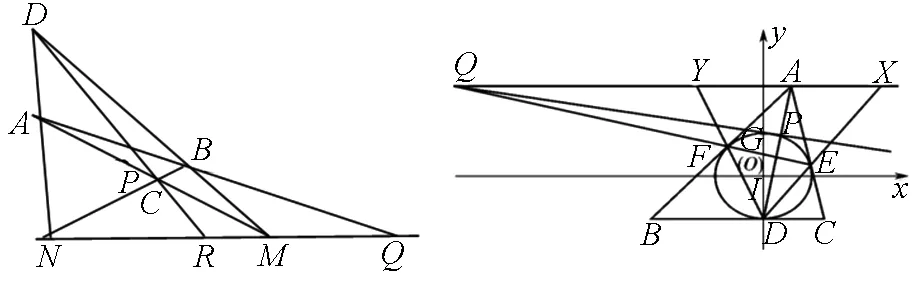
图1 图2

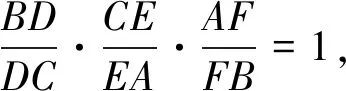
取完全四边形AFIE，记AD与FE相交于P，FE与BC相交于Q1，由引理1得F、E调和分割P、Q1.于是直线DX、DY调和分割直线DA、DQ，设直线BC与AQ交于R.若证得点R为无穷远点，即证明BC∥QA，则竞赛题获得证明.

下面，我们采用可以进行推广的证明方法,证明BC∥QA.

此时，由AD⊥PQ，知直线PQ必过⊙O的直径DG的端点G.现给出仿射推广的证明方法.

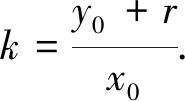
现利用仿射变换，给出考题的推广.

命题1 在△ABC中,∠B≠∠C,△ABC的内切圆⊙O(一直径为DG)与BC、CA、AB的切点分别为D、E、F.记AD与⊙O的不同于点D的交点为P.连接PG交EF于点Q,X、Y分别是AQ与直线DE、DF的交点.求证:A是线段的中点.

命题2 在△ABC中,∠B≠∠C,△ABC的内切椭圆Γ(一主轴为DG)与BC、CA、AB的切点分别为D、E、F(其中切点D为椭圆一顶点).记AD与Γ的不同于点D的交点为P.连接PG(G为椭圆另一顶点，)交EF于点Q,X、Y分别是AQ与直线DE、DF的交点.求证:A是线段的中点.

现在，给出命题2的证明.

证明：(1)证明AD、BE、CF交于一点.

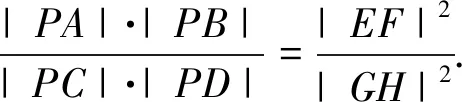
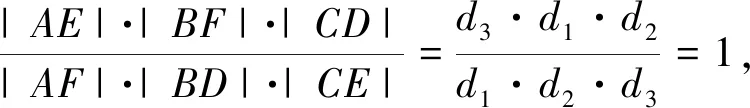
(2)证明BC∥QA.

在证明(1)中，又得到结论：

命题3 在△ABC中,∠B≠∠C,△ABC的内切椭圆Γ与BC、CA、AB的切点分别为D、E、F.则直线DE、DF调和分割直线DA、DC.

同时，对于三角形的内切圆具有仿射不变性.

即三角形关于内切圆的赛瓦定理，在三角形关于内切椭圆的赛瓦定理依然成立.