β-Ga2O3电子结构、光学性质及激子效应研究
2019-08-30杨创华
杨创华
(陕西理工大学 物理与电信工程学院, 陕西 汉中 723000)
超宽带隙(UWBG)半导体材料氧化镓(Ga2O3)因其独特的材料特性而成为下一代高功率电子器件和深紫外(DUV)太阳能盲光电探测器的新竞争者[1-2]。在5种已知的Ga2O3相结构(α、β、γ、δ和ε)中,具有单斜晶体结构的β相Ga2O3是最具热稳定性的材料[3]。β-Ga2O3的室温带隙大约为4.5~4.9 eV[4-6]。它在高温下还具有优异的化学、机械和热稳定性。其超宽带隙对应于大约250 nm的截止波长,属于太阳光的盲光区。因此,基于β-Ga2O3的太阳盲光光电探测器不需要任何辅助滤波器,不需要被合金化,简化了材料生长过程,降低了成本[3]。基于β-Ga2O3的场效应晶体管和二极管由于其非常大的带隙而可以具有优异的功率器件特性,例如高击穿电压、高功率和低损耗。基于带隙Eg和击穿电场Ebr之间的经验关系,预期β-Ga2O3的Ebr具有约6~8 MV/cm的值[7]。高Ebr是β-Ga2O3最具吸引力的特性。Baliga的品质因数(FOM)是评估材料适用于功率器件的基本参数,与Ebr成正比[8],击穿电场越大,Baliga的品质因数就越高。与SiC和GaN相比,在相同的击穿电压下,β-Ga2O3功率器件的传导损耗可以低一个数量级。更有利的,可以通过可扩展和低成本的熔体生长技术大量合成高质量的β-Ga2O3晶片。这解决了目前基于SiC和GaN的器件制造中,衬底无法低价大量生产的限制。
尽管近年来对β-Ga2O3材料生长及器件制作的研究越来越多,但对β-Ga2O3基础物理性质的理解还不清楚。这些基础物理特性是制作电子器件的理论基础,对这些特性的准确描述是具有重要意义的。β-Ga2O3的基础物理特性电子结构和光学性质目前只限于基于密度泛函理论(DFT)的PBE赝势的方法计算的报道[9-10]。众所周知,PBE高估晶体的晶格常数、低估材料的能带带隙,不能准确的描述β-Ga2O3的电子结构及光学性质。因为β-Ga2O3是超宽禁带半导体,有可能其中的激子效应会比较明显,进一步会影响它的光学性质。因此本文基于自洽的准粒子近似(GW近似)修正计算β-Ga2O3的电子结构,在考虑激子效应(电子-空穴对的库伦相互作用)的基础上,通过求解Bethe-Salpete方程(BSE)计算β-Ga2O3的光学性质。
1 算法描述
所有的计算我们都是采用Vienna ab initio Simulation Package(VASP)代码的从头算方法执行的[11-12]。首先采用基于DFT算法进行几何优化及静态计算,交换相关电位采用广义梯度近似(GGA)的PBE形式[13];其次在静态计算的基础之上采用杂化泛函(HSE)[14]的方法计算电子结构和光学性质;最后采用GW+BSE的方法修正计算结构以及求解精确的光学性质;投影仪增强波(PAW)[15]方法用于描述核心电子。通过测试,选取平面波基组截止能为400 eV。最佳原子位置和晶格结构完全驰豫,总能量的收敛标准和最大力的阈值分别设定为10-6eV和10-4eV/Å。对于布里渊区域积分,k点采用9×9×1 Gamma中心网格Monkhorst-Pack k-mesh方案。在这个工作中,对于DFT部分和HF部分μ都被设置成0.3,也就是所谓的HSE03方案[16]。0.05 eV的高斯展宽用来展开单电子的能级。在接下来的GW计算中,GW0计算方法被采用[17-19],240个空导带被包含,其中自能量算子Σ几乎包含所有电子-电子交换和相关效应。从GW0计算开始,可以使用最大局部化Wannier函数(maximally localized Wannier functions,MLWF)方法对QP能带结构进行插值,最终得到材料的能带结构。为了计算光学性质,GW方法加随机相位近似(RPA)被首先采用[20-21](不考虑电子-空穴的相互作用)。然后在GW+RPA基础之上,通过考虑准电子和准空穴之间的库伦相互作用求解BSE方程[22-23]。BSE方程的求解中包括了24个最高价带和24个最低导带作为激子态的基础,使用Tamm-Dancoff近似[24],得到材料最终的光学性质。
2 结果和分析
2.1 几何结构
在所有Ga2O3的多晶型中,由于β-Ga2O3出色的热稳定性和多种优秀的特质,引起了最多的关注。它是5种同分异构体中在整个温度范围内(直至熔点)唯一稳定的多晶型物。β-Ga2O3属于C中心的单斜晶胞,对称性为C2H-3,对应的空间群为C2/m。它的晶格常数分别为:OA=a=12.23 Å,OB=b=3.040 Å,OC=c=5.807 Å,α=γ=90°,β=103.8°。本文中,我们首先构建了本征的β-Ga2O3惯用晶胞晶体结构,如图1所示。它包含两个结晶学上不等价的Ga位置,Ga(I)和Ga(II)。Ga(I)和其周围的4个O原子成键,形成一个变形的四面体结构;Ga(II)和其周围的6个O原子成键,形成一个变形的八面体结构。根据O原子与Ga原子的相对位置,氧原子具有3个结晶学上不同的位置,分别表示为O(I)、O(II)和O(III)。O(I)是三价离子,连接了2个四面体和一个八面体;O(II)为四价离子,处于3个八面体和一个四面体交汇处;O(III)也是三价,位于2个八面体一个四面体的交点。2个氧原子三角配位,一个四面体配位。
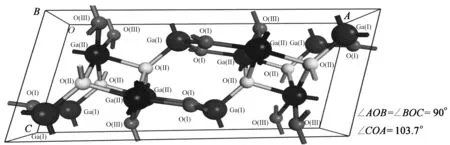
图1 β-Ga2O3惯用晶胞的晶格几何结构
β-Ga2O3晶体是由[GaO6]八面体构成的双链沿b轴方向排列而成,链与链之间以[GaO4]四面连接,这种结构有利于电子的移动,使β-Ga2O3在结构上具备导电的可能性。
表1是基于PBE泛函计算出的平衡状态下的β-Ga2O3的晶格参数。由表可知计算出的结果与理论计算的结构[24-25]及实验结果[26]相一致。从计算出的晶格常数和基矢之间的夹角,可以看出β-Ga2O3属于单斜晶体。同时显示出理论计算的晶格常数都比实验的结果大一些,这是主要由于PBE泛函的缺陷造成的。但是基于PBE计算优化的晶格结构参数,对于我们研究晶体的电子结构、光学性质等物理特性的影响可以忽略。

表1 计算出的β-Ga2O3惯例晶胞的晶格几何参数与其他文献结果对比
图1所示的惯例晶胞的晶胞矢量由下式给出:
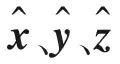
a1prim=(a1conv+a2conv)/2,
a2prim=(-a1conv+a2conv)/2,
a3prim=a3conv,
其中上标prim、conv分别表示原胞和惯例晶胞向量。原胞包含10个原子,结构图如图2所示。
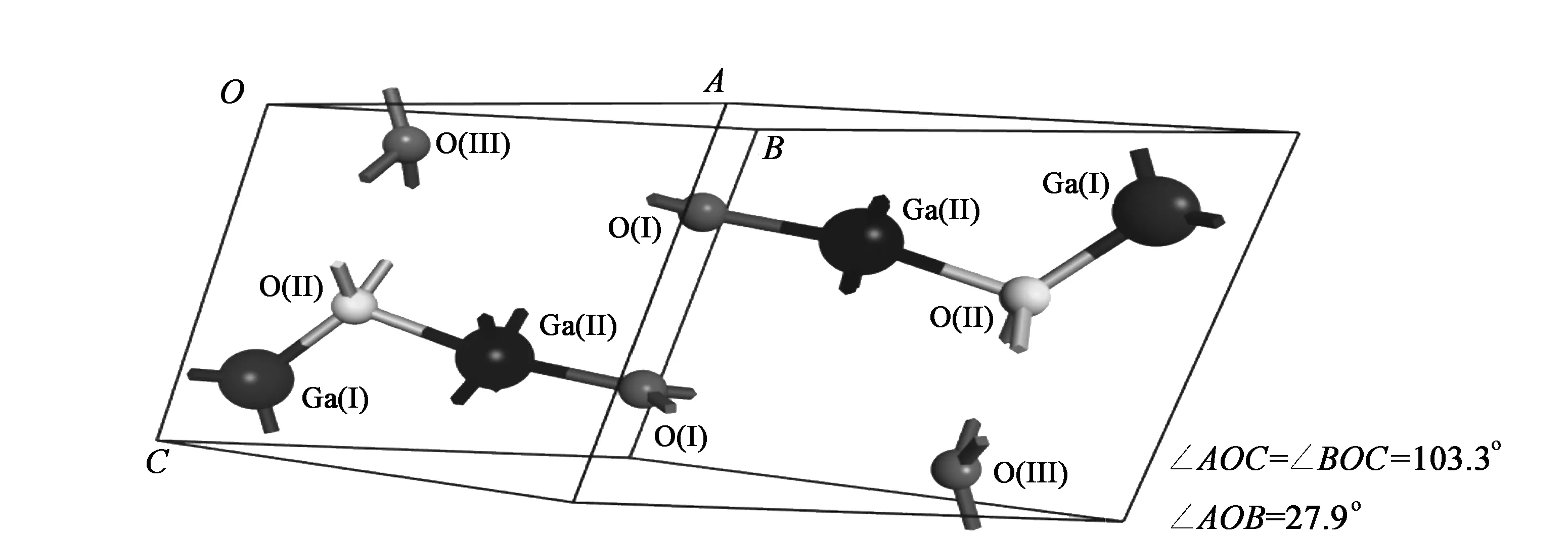
图2 β-Ga2O3原胞的晶格几何结构
在单斜晶系中,布里渊区的形状非常依赖于晶格矢量。晶格矢量的长度和它们之间的夹角直接影响单斜晶体的布里渊区。为了避免这个问题,经常使用以k=0为中心的倒格矢平行六面体代替布里渊区,即使在教科书和在线晶体学数据库[26]也这样来做。该方法无法识别许多高对称线和点,也不能保证连接该平行六面体上的两个点的线是高对称线。即使使用的布里渊区域被正确定义,对晶格向量的非平凡依赖性也可能导致其他问题:当计算的晶格向量与实验值差别较大时,可能出现布里渊区明显的不同。实际上,在单斜晶系中,可能有5种不同形状的布里渊区[27-28]。
一些研究者使用对应于惯例晶胞的倒易晶格矢的平行六面体来计算能带结构[2,29-30]。但是使用惯例晶胞的倒格矢和使用原胞倒格矢的论文都使用了相同的高对称点的标签[31]。然而对应于惯例晶胞倒格矢的平行六面体比原胞倒格矢平行六面体的体积小的特点,因此如果采用惯例晶胞,则原胞的不可约布里渊区域将不会完全地跨越。一些研究者又展示了一个更复杂的布里渊区域,但其形状并不正确[28]。先前在文献中已经描述了单斜晶体结构的5种可能的布里渊区形状,但是没有发现使用此正确布里渊区形状计算β-Ga2O3的文献报道。
本文通过清晰地和正确地计算完整的β-Ga2O3布里渊区域来解决这些不足,使用GW方法获得β-Ga2O3的准确电子结构,由此得到准确的能带结构、带隙等信息,有利于和有限的实验信息进行比对。
基于优化所得到的原胞结构,得到倒易格子的Wigner-Seitz单元。利用二等分方法以获得布里渊区。使用的高对称点的倒易空间坐标列于表2中,Ψ、φ、ζ、η表示为取决于晶格参数的4个变量的函数:

表2 β-Ga2O3倒易空间布里渊区高对称点的坐标
2.2 能带结构
基于PBE、HSE和GW方法计算的β-Ga2O3的基本能隙(Eg)、光学带隙性质(Ef·p)、紧束缚激子的结合能(Etb)、最大吸收峰对应的能量值(Em·p)总结如表3。由表可看出:PBE明显的低估了能带带隙,GW计算的能带带隙的结果跟实验结果4.5~4.9 eV[6,29,32]恰当吻合。

表3 不同方法计算β-Ga2O3的基本带隙

图3 β-Ga2O3沿布里渊区高对称点的能带结构
在图3中,给出了使用上述原胞和布里渊区基于GW计算得到的β-Ga2O3的能带结构。我们定义了一条覆盖相同高对称线的路径,但避免了不连续性。导带最小值位于Γ点位置,价带最大值位于I—L线上。之前没有报道过这个价带最大值的位置。由于价带的小的色散,其精确位置基本上不影响带隙的大小。基本带隙是间接的,其幅度为4.63 eV。直接带隙为4.67 eV,两者之间的差仅为0.04 eV。所以可以看成是直接带隙半导体。
在Γ点能带的电子有效质量也进行了计算。它们几乎是各向同性,其值在0.27me~0.28me之间。这些值与实验测量结果以及使用HSE计算的结果相吻合[28]。在局部密度近似(LDA)中为0.23me~0.24me,在广义梯度近似(GGA)中为0.12me~0.13me[2]。价带几乎是平的,表明空穴的有效质量相当大。
2.3 光学性质及激子效应
采用GW+RPA方法和GW+BSE方法计算的沿3个方向极化的β-Ga2O3介电函数虚部对比图如图4(a)所示。对比GW+RPA方法计算的光学性质,我们发现β-Ga2O3的光学性质在xx、yy和zz三个极化方向上是各向异性的。吸收带边对应于β-Ga2O3能带Γ点附近的直接跃迁。不考虑电子-空穴计算的光学性质,主要由价带电子到导带的直接跃迁来决定。从图上可以看出,在考虑了电子-空穴之间相互作用后的GW+BSE计算后,光学性质相对于GW+RPA的计算结果有很大的改变。两种方法计算的三个极化方向光学性质曲线相差较大,GW+BSE计算的光学性质的吸收带边发生了红移,在准粒子直接带隙以下都有显著的吸收峰,吸收强度增强。由于没有其他杂质存在,这些吸收峰显然是束缚的激子吸收峰,说明β-Ga2O3中有比较强的激子效应。这与传统的宽禁带半导体材料金刚石(diamond)、SiC以及AlN等的光学性质和激子效应[33]相一致。

(a) 极化方向的β-Ga2O3介电函数虚部 (b) 极化方向的吸收系数 图4 β-Ga2O3沿xx、yy、zz方向极化计算方法函数对比图
xx极化方向,光学性质在4.38、4.90、5.39、6.29 eV出现了吸收峰,6.29 eV出现的吸收峰最强。最低的4.38 eV对应于光学带隙。从能带结构计算结果看出,β-Ga2O3的基本带隙是4.67 eV的直接带隙。之所以在基本带隙能量之下产生了光吸收峰,也就是说光学能隙小于电子能隙,这是由于激子的光吸收作用,对应于束缚激子的吸收峰,激子束缚能为0.29 eV(4.38~4.67 eV)。它主要是由于Γ点附近的电子-空穴对间的相互作用而形成。另外从BSE光谱中还可以看出,强度最大的吸收峰位于6.29 eV处。由于该峰能量大于直接带隙能量4.67 eV,所以这个激子峰是共振激子峰。在yy极化方向的基于GW+BSE计算的光学性质主要出现了5.05、5.69、6.92 eV等吸收峰。光吸收从大约4.5 eV左右就迅速增加,这个值也小于基本电子能隙4.67 eV,而且GW+BSE计算的光学吸收在4.5~11 eV的能量范围内都远远强于GW+RPA计算的光学吸收强度。在zz极化方向上基于GW+BSE计算的光学性质,主要出现了4.14、4.78、5.92、7.70、8.13 eV等吸收峰。在4~9 eV的能量范围内,GW+BSE计算的光学吸收谱都远远强于GW+RPA计算的吸收谱。第一个吸收峰出现在4.14 eV能量处,这个值小于基本的带隙4.67 eV,这是一个束缚态的激子峰,对应的激子束缚能为0.53 eV(4.14~4.67 eV)。大于基本带隙4.67 eV的吸收峰对应于共振激子的吸收峰。
基于GW+BSE计算了介电函数虚部,并通过介电函数与吸收系数的关系求解出了β-Ga2O3吸收系数随能量变化的曲线,如图4(b)所示。从图上可以看出,在xx、yy和zz三个极化方向上,β-Ga2O3在光带隙能量以下几乎没有光吸收,在能量大于光带隙以上都具有数量级为105cm-1的吸收系数。
光的吸收实际上集中在晶体很薄的表面层内。这是由于半导体材料内部有自由电子存在,光波在传播过程中在导电媒质内激起传导电流,光波的部分能量转换为电流的焦耳热。通过对应的左、右图的比较,我们发现介电函数与吸收系数所对应的吸收峰能量值是一致的,这也验证了介电函数虚部与吸收系数之间的正比例关系。在xx极化方向上有4个峰,对应的能量值为4.39、4.91、5.40、6.30 eV,吸收系数分别为2.09、1.81、1.84、6.62;在yy极化方向上主要有3个吸收峰,对应的能量值为5.06、5.71、6.94 eV,吸收系数分别为3.67、4.22、6.42;在zz极化方向上主要有4个吸收峰,对应的能量值为4.15、4.80、5.92、7.75 eV,对应的吸收系数为2.25、3.08、6.18、7.99。
综上所述,激子效应较大的影响了β-Ga2O3的光学性质,计算它的光学性质需要靠包含激子效应的GW+BSE方法。计算结果表明要想准确的计算和表征β-Ga2O3的光学性质必须考虑到它的激子效应。
3 结 论
基于GW近似修正计算了β-Ga2O3的电子结构,计算得到的能带带隙为4.67 eV,与实验的相一致。计算了在Γ点能带的电子和空穴有效质量,结果显示它们几乎是各向同性,其值在0.27me~0.28me之间。价带几乎是平的,表明空穴的有效质量相当大。在准确计算β-Ga2O3电子结构的基础上,包含激子效应计算了它的光学性质。计算的结果表明β-Ga2O3激子效应非常明显,较大的影响了它的光学性质,所以要计算它的光学性质需要采用包含激子效应的GW+BSE方法。此计算结果将为利用β-Ga2O3制作光电器件打下良好的理论基础。
