基于模糊聚类的并行推荐算法

张开生， 宋文伟， 李慧贞

(陕西科技大学 电气与信息工程学院， 陕西 西安 710021)

自互联网发展开始，网络数据呈现出爆炸式的增长趋势，用户往往需要消耗大量的精力和时间来筛选自己真正想要的并且有价值的信息。目前，协同过滤算法是使用最广泛和最成功的推荐策略，但协同过滤推荐算法仍然存在稀疏性、可伸缩性、冷启动等问题。为此，许多学者提出了各种方法来提高推荐算法的性能。涂丹丹等[1]为解决数据稀疏性问题提出了基于联合概率矩阵分解的因子模型AdRec，该模型结合了网页、广告和用户三维数据生成推荐结果。孔欣欣等[2]提出一种基于标签权重评分的推荐系统模型，旨在使用标签权重评分来获取用户最准确的评价和需求，从而生成对用户的推荐。肖文强等[3]为解决冷启动问题引入用户通用评分权重和热门项目权重可提高推荐算法的准确性。黄震华等[4]引入排序学习，以此整合海量用户、物品特征，建立最贴合用户偏好需求的用户模型。为解决伸缩性问题，孙天昊等[5]提出在分布式平台下，引入并改进聚类协同过滤推荐算法。基于此，本文对基于模糊聚类的并行推荐算法进行了研究,采用PCA(Principal Component Analysis)降维，保留最能代表用户特征的数据，结合模糊聚类特点，改善传统协同过滤中因数据稀疏导致的最近邻划分不准确问题，从而提高推荐质量。

1 传统的协同过滤推荐算法

协同过滤的主要思想是，在海量数据集中探索与用户品味最相似的K个用户组成邻居，并根据这K个用户对当前用户未评级项目的打分，预测当前用户对其未评级项目的评分，最后选择前n个用于推荐。算法主要由以下3个步骤组成。

1.1 建立用户评分关系矩阵

在对用户的行为数据进行预处理之后，用Rm×n表示用户对推荐对象的评级信息，即用户评分矩阵：

(1)

其中Rij表示用户i对对象j的评估。得分可以是一系列值，例如0～5，不同的值表示用户喜好推荐对象的程度。也可以是0或1，代表用户喜欢或用户不喜欢。

1.2 相似度计算

在推荐系统中，对象相似度[6-7]的计算方法是提高推荐准确性的关键之一。可使用某用户对所有项目的偏好作为向量来计算用户之间的相似性，或将所有用户对某项目的偏好用作向量来计算项目之间的相似性。在不同的推荐场景中，所选择的相似度的计算方法也不同。本文中，Pearson相关系数用于计算相似性。Pearson相关系数通常用于计算两个距离变量之间关系的接近程度，其值在[-1，+1]之间，计算公式如下:

(2)

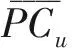
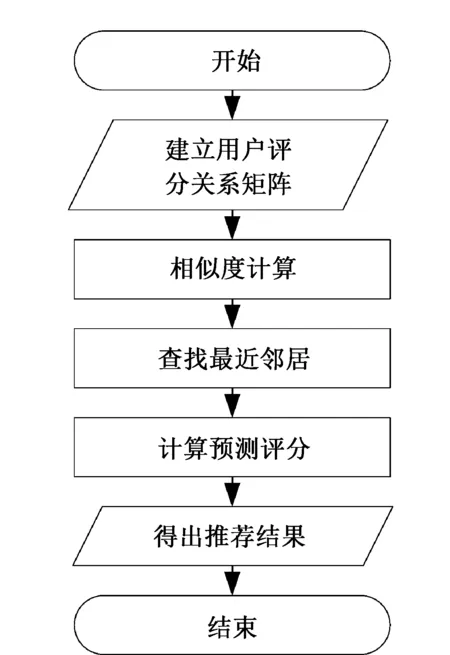
图1 传统协同过滤 推荐算法流程

1.3 产生推荐

对计算出的相似度排序，选取用户的前N个最近邻居，可以对该用户未评分的项目进行预测，预测方法如下:

(3)

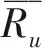
2 基于模糊聚类的并行推荐算法研究

虽然传统的协同过滤推荐算法被广泛使用，但在实际应用中经常存在一些挑战和不足。由于传统的协同过滤算法相似度计算，需要遍历整个用户物品矩阵，随用户量和物品量的增长，计算量持续增加，响应推荐请求的系统效率降低，存储器开销也随之增加。使用明尼苏达大学项目研究组Grouplens发布的MovieLens数据集，当邻居N数量为10且推荐数量为30时，统计传统协同过滤推荐算法的平均推荐耗时，其中抽样等级S1(2555-250)表示从2555个用户中抽取250个用户，抽样等级S2(1915-190)表示从1915个用户中抽取190个用户，如表1所示。

表1 传统的协同过滤推荐耗时

可知，在整体数据集用户数量只有3883，电影数量只有6040部的情况下，传统协同过滤推荐算法的运行时间至少大于1 min。在实际应用中，面对数以万计的用户及推荐对象，单凭这样的推荐速度会严重影响用户体验。为此，本文研究了一种基于模糊聚类的并行推荐算法。针对数据维度高、计算量大的问题，原始数据由PCA技术和FCM(Fuzzy C-means)聚类预处理,降低数据维度、减少计算次数。后利用得到的聚类簇集合建立最近邻集合，生成基本预测评分并作出推荐。以上操作均在Hadoop集群上运用MapReduce[8]计算框架完成。算法流程如图2所示。

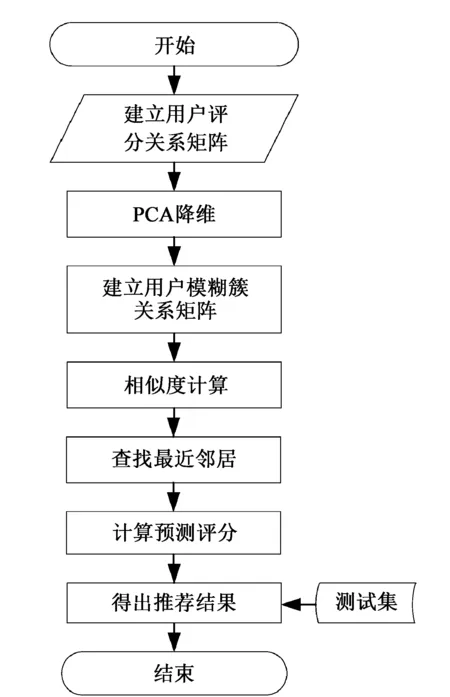
图2 并行推荐算法流程

2.1 PCA降维

在实际使用时，推荐系统中的用户数量和推荐对象的数量非常大，并且生成的用户项目矩阵维度非常高。迫切需要引入降维方法进行优化，PCA正是一种在尽可能减少信息损失的情况下降低数据维度的方法，通过正交变化，可以用少量新变量来解释原始数据的大部分信息[9]。通常，提取原始数据中95%的信息就可以实现良好的降维效果。算法描述如下：

Ⅰ 输入m×n的初始数据矩阵X和设定的主成分数量k；

Ⅱ 计算初始数据矩阵X的协方差矩阵Cn×n；

Ⅲ 对协方差矩阵Cn×n作奇异值分解，计算协方差矩阵Cn×n的特征值和特征向量e1、e2、…、en，返回由特征向量组成的n×n降维矩阵U，其中矩阵U上每列数据都是一个特征向量；

Ⅳ 取出降维后矩阵U的前k列数据，得到n×k的投影矩阵P；

Ⅴ 最后原矩阵X乘以投影矩阵P，得到目标矩阵。

2.2 模糊C均值聚类

模糊C均值聚类(FCM)算法是对早期硬C均值聚类(HCM)算法的一种改进，其主要思想是通过隶属度来表达各数据点隶属某聚类的程度。FCM的主要改进在于摒弃了暴力的0、1取值，FCM用模糊划分，隶属度采用[0,1]取值区间来确定[10]。算法描述如下：给定数据集X={x1,x2,…,xn}包括n个样本，数据集可以划分为c(1≤c≤n)类，那么，FCM的目标函数可定义为：

(4)

其中U表示隶属度矩阵,uij∈[0,1],ci表示组i的聚类中心,dij=‖Hi-Xj‖表示数据点j与各聚类中心之间的欧式距离,m∈[1,+∞)是一个加权指数。使(4)式逼近最小值的必要条件为

(5)

(6)

算法主要步骤如下:

步骤1:用随机生成的[0,1]区间内的数来初始化隶属度矩阵;

步骤2:用式(5)对各聚类中心进行初始化;

步骤3:通过式(4)得到目标函数，多次迭代，若目标函数的变化量小于ε(ε表示非常小的数)，算法停止;

步骤4:用式(6)更新隶属度矩阵，回到步骤2执行。

3 基于模糊聚类的并行推荐算法的流程

3.1 建立用户模糊簇关系矩阵

通过对原始数据进行模糊聚类，得到相应的模糊簇，用式(7)计算项目对各模糊簇的隶属度：

(7)

其中xi、mj分别代表各项目和各簇中心的属性特征向量，‖xi-mj‖表示项目i与各簇中心的欧氏距离，c表示簇数量。

通过原始数据中用户评分和各项目对簇的隶属度，用式(8)计算用户u对各个簇j的偏好值，从而建立用户-模糊簇关系矩阵：

(8)

式中Su,j表示用户u对簇j的偏好值，Ru,i表示用户u对归属于簇j的项目i的偏好值，Iu表示u个用户建立的用户评分集合。对用户-模糊簇关系矩阵进行PCA降维计算，舍弃掉特征值较小或为0的特征向量，计算每一维数据的投影，该投影矩阵即为该样本集合的主成分。

3.2 构建最近邻集合

获取降维后的用户模糊簇关系矩阵，用式(2)计算用户间相似度值，生成用户的最近邻集合。

3.3 得出推荐结果

从最近邻集合中获取与当前用户具有最高相似度的m个邻居。根据式(3)预测邻居购买但未被目标用户购买的项目分数，并选择Top-N进行推荐。

4 实验仿真与分析

4.1 实验环境

根据以上研究，使用5台PC机搭建Hadoop平台，包括1个Master节点和4个Slave节点，运行环境为Ubuntu14.04，Hadoop版本为2.6.0，集群配置[11]如表2所示。

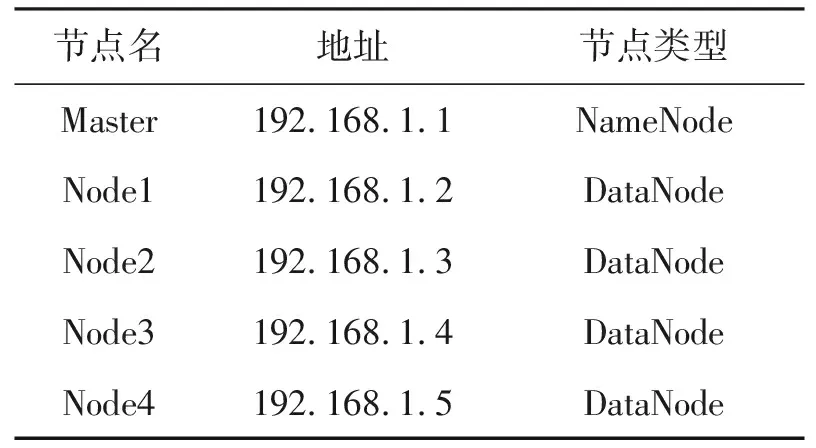
表2 Hadoop集群配置信息

4.2 数据集合

实验主要采用明尼苏达大学GroupsLens小组发布的Movielens数据集，从http://grouplens.org/datasets/movielens/站点下载大小分别100 KB、1 MB、10 MB的数据集进行实验。各数据集内容如下：(1)100 KB：共有943位用户评分了1628部电影，共计90 582个记录；(2)1 MB：共有6040位用户评分3900部电影，总计1 000 209个记录；(3)10 MB：共有71 567位用户对10 681部电影评分，总计10 000 054个记录。分数从1～5，值越高，用户对电影的喜爱程度越高。

4.3 度量标准

推荐系统的评估标准可以反映推荐系统预测用户行为的能力，本文主要测量平均绝对误差(MAE)和加速比。平均绝对误差方法是推荐精度的常用度量方法。加速比是在单处理器系统和并行处理器系统中运行相同任务所花费的时间的比率，通常用于衡量并行系统或程序并行化的性能和效果[12]。

设pi是系统对项目i的预测得分，ri是用户项目的实际得分，N是预测项目数,MAE可定义为

(9)

设Tp表示存在p个处理器时并行算法的执行时间，T1表示顺序执行算法的执行时间,加速比可定义为

(10)

4.4 实验过程及分析

(1)MAE比较

如表3所示，取100 KB数据集作为实验数据，选取用户数量分别为25、100、200、400、800的集合作

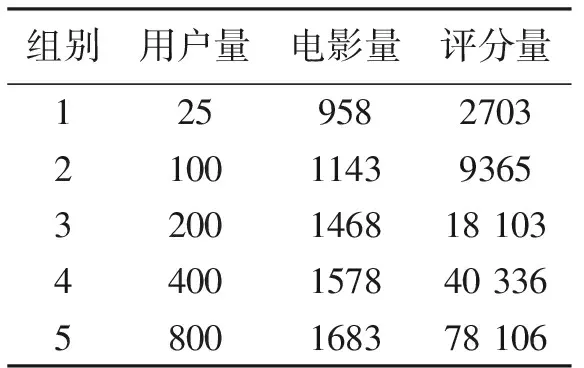
表3 实验数据

为本实验的5组实验数据。随机选择组中80%的数据作为训练数据，并将20%的数据用作每组实验数据中的测试数据。

图3将本文研究的基于模糊聚类的并行推荐算法，同传统协同过滤和基于PCA降维的协同过滤做性能上的对比分析。从图中可以看出，本文算法具有较小的MAE并且MAE值随着实验数据量的增加而减小，这意味着推荐精度的不断提高。PCA降维将最能反映用户兴趣的特征保留下来，剔除了噪声数据，改善了数据稀疏性,降低了计算复杂度，故传统CF算法的MAE值明显较大。

(2)加速比分析

本实验通过逐个增加DataNode节点个数改变Hadoop集群的处理能力，比较得出在不同规模的Hadoop集群下执行算法对算法执行效率的影响。分别在1—4台计算节点上对MovieLens在100 KB、1 MB、10 MB三个不同数据集进行加速比计算，绘制加速比曲线图如图4所示。

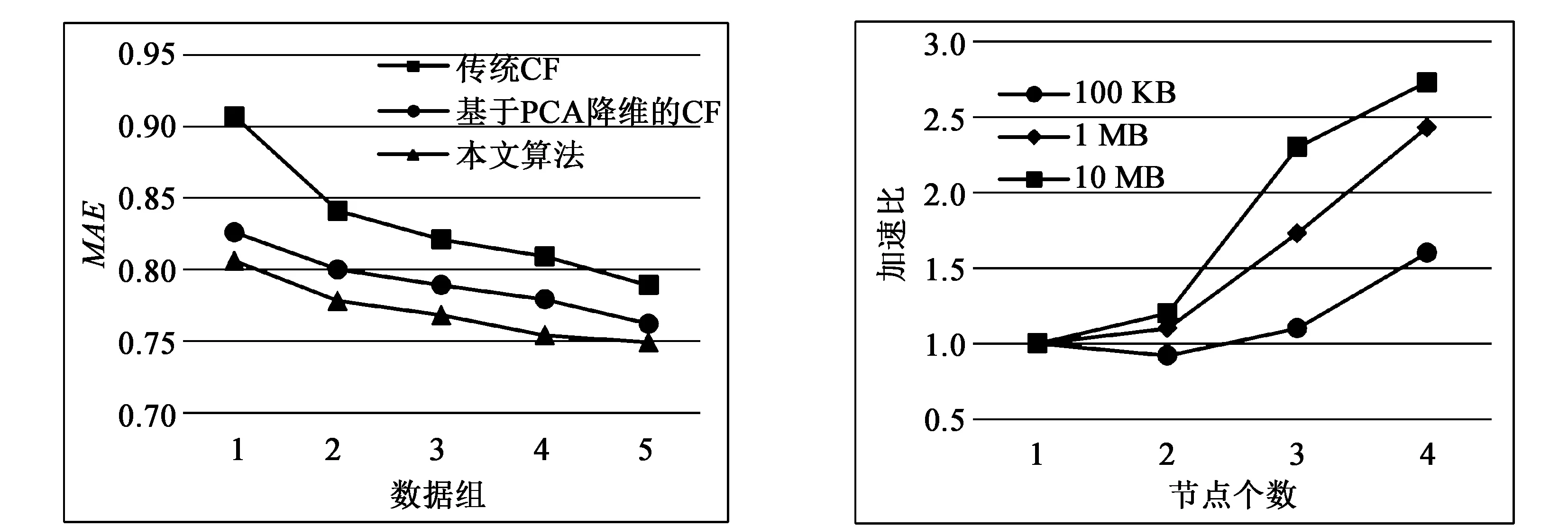
图3 MAE对比图 图4 加速比曲线图

从图4看出，随节点个数递增，处于3种不同数据集下的算法加速比也递增。若数据集保持不变，加速比随节点数量的增加而增大。若数据集改变时，数据集越大，加速比随节点数量增大的幅度越大。当节点数量小于3时，节点不仅需要处理计算任务，还需要调度资源，故加速比变化率较小。但是，当集群中的DataNode节点数大于3时，加速比线性增加。因此，本文算法可以提高推荐效率，并在并行化环境中具有可扩展性。