有机发光激子的演化过程研究

曾俊杰 刘玲 张勇*

（西南大学物理科学与技术学院，重庆 400715）

1 概述

单重态激子的裂变(简称激子裂变)，是一种在某些特殊有机半导体材料中激子数倍增的现象，其具体形式为：在这些材料中，由光或电激发产生一个具有较高能态的单重态激子S1，而后S1态激子将其一半的能量转移给另一个处于基态的分子S0，而后S1态激子和S0态分子快速转变为两个具有较低能态的三重态激子T1。另外，激子裂变过程是可逆的，其逆过程被称为三重态激子的聚变(简称激子聚变)，一般情况下这两种过程共存。在半导体物理中，激子的本质是一对通过库仑作用束缚在一起的电子- 空穴对。首先，这些具有激子裂变特性的有机材料同样具有光吸收特性，通过吸收辐射光子能量来产生电荷对，电荷对解离即产生光电流。然后，材料借助激子裂变过程进一步实现电荷数量的倍增，普通光伏材料吸收一个光子只能产生一对电荷，而激子裂变材料吸收一个光子可望产生两对电荷。最后，有机材料中T1态激子的总自旋为1，回到基态需要其中一个电荷完成自旋翻转，这使得T1态激子的衰减时间远高于S1态激子并由此获得更长的扩散距离，因此更容易到达界面附近实现电子和空穴的分离。若能充分利用上述三种有利因素，可使得光伏器件的最高效率从34%提升至45%。

在此前的研究中，激子裂变的演化过程通常用一个传统的两步三状态演化模型来描述[1]：

其中的1(TT)i态是由两个T1态激子耦合形成的中间过渡态，其中k-2，k2，k-1，k1是不同状态间相互转化的速率。然而，最近的一些研究表明[2,3]，当1(TT)i 态向(T1+T1)态转变时，其转变过程并非如公式(1)那样简单直接。近期报道的研究揭示，两个T1态激子先经过空间上的分离，其空间波函数的交叠首先解除，但此时二者间仍然保持自旋相互作用，形成另一个中间过渡态1(T…T)，再经过退相干过程令自旋相互作用消失，最终使得两个T1态激子转变为两个相互独立的T1激子，即公式(1)中的(T1+T1)态。按照上述描述，新的激子裂变演化过程可以用一个改进的三步四状态演化模型来描述[2,3]：

其中k-2，k2，kD，kC，k-1，k1均为不同状态间相互转化的速率。值得注意的是，对上述新增的中间过渡态1(T…T)，已有的实验报道不多，尚缺乏有力的实验证据支持。

激子裂变过程需满足能量守恒要求，两个T1态激子的能量2E(T1)主要来源于S1态激子的能量E(S1)，因此裂变条件可以简单表示为E(S1) ≈2E(T1)。以并五苯(pentacene)材料为例，E(S1) = 1.83 eV，2E(T1) = 1.72 eV，二者间能量差为E(S1)-2E(T1) = 0.11 eV，说明在并五苯材料中的裂变过程为放热反应。而在并四苯(tetracene)材料中，其E(S1) = 2.32 eV，2E(T1) = 2.50 eV，二者间能量差为E(S1)-2E(T1) = -0.18 eV，说明在并四苯材料中的裂变过程为吸热反应。在红荧烯材料中，其E(S1) = 2.23 eV，2E(T1) = 2.28 eV，二者间能量差仅有0.05 eV，说明在红荧烯材料中的裂变过程也是吸热反应，但由于能量差相当小，故在红荧烯材料中可发生快速的激子裂变过程。本实验中，以红荧烯材料为研究对象，在不同温度下测量了红荧烯薄膜的光致发光谱及其瞬态发光衰减曲线。为了研究红荧烯材料中的发光激子演化过程，基于两步三状态演化模型和三步四状态演化模型，分别利用两组耦合的微分方程组对不同温度下的发光衰减曲线进行理论拟合。拟合结果显示，将不同温度下的理论拟合曲线和实验测量曲线叠加比较后，相较于两步三状态模型，基于三步四状态模型所得的拟合曲线与实验曲线的符合度更好。

2 实验结果与分析

一般的，通过普通热蒸发方式获得的红荧烯薄膜总是呈现出非晶态结构。在本实验中，红荧烯薄膜的厚度为100 nm，蒸发速率维持在～0.6 /s，热蒸发前真空度达到～1×10-5Pa，所用石英玻璃衬底始终保持在室温。使用Edinburgh FL920 稳态/瞬态荧光谱仪分别在不同温度下(300 K、250 K、200 K、150 K、100 K、50 K) 测量了红荧烯薄膜的光致发光谱及其瞬态发光衰减曲线。光致发光的激发光波长为350 nm，激发光的强度约2 mW。

如前所述，由于红荧烯分子的E(S1) ＜2E(T1)，故红荧烯分子的激子裂变过程是一个吸热过程，当温度降低时激子裂变过程被抑制，发光激子有更大的概率通过辐射复合方式衰减，因而造成薄膜的光致发光强度随温度降低而逐渐增强，同时在低温下发光峰变得更尖锐。图1 展示的测量结果与预期一致。插图展示了红荧烯分子在低浓度掺杂下的光致发光谱。即将红荧烯分子以2%的质量比均匀掺杂在完全惰性的有机分子NPB 中，NPB 分子在混合薄膜中起到间隔作用，目的是将红荧烯分子分开。在低浓度掺杂时，由于红荧烯分子处于非常稀释的状态，相邻红荧烯分子间距离太大，不能发生激子裂变过程，虽然随温度降低发光峰同样变得更尖锐，但发光谱线下的面积基本不变。图2 展示了实验所使用的FL920 稳态/ 瞬态荧光谱仪的仪器响应函数(instrumental response function，简称IRF)曲线，作为对比图2 中还画出了红荧烯在300 K 和50 K 时的发光衰减曲线。该型仪器的响应时间可以由测量曲线的半高宽来量度，图2 中IRF 曲线的半高宽约为0.64 ns，远远小于红荧烯材料中的激子衰减的平均寿命，表明仪器对红荧烯薄膜瞬态荧光衰减的响应足够快，测量结果足够准确。

图1 不同温度下红荧烯薄膜的光致发光谱

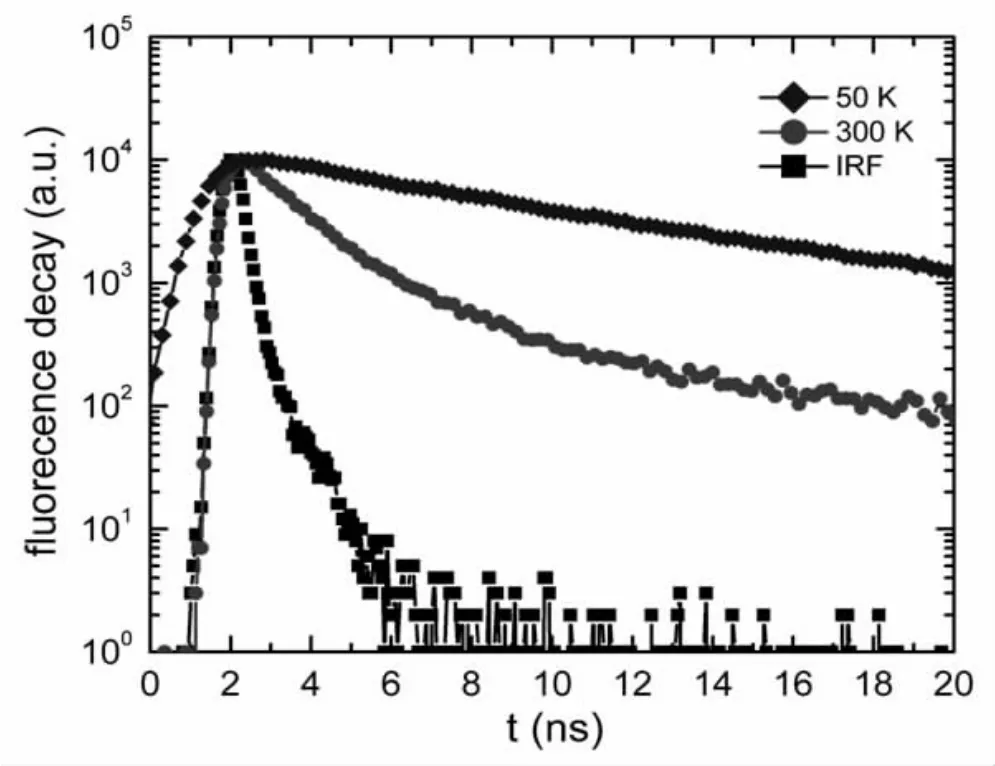
图2 瞬态光谱仪的仪器响应函数（IRF）曲线

基于两步三状态演化模型，可列出如公式(3)所示的耦合的微分方程组来对发光的衰减过程进行描述，其中NS为S1态激子的数量，ND为中间过渡态1(TT)i的数量，NT为(T1+T1)态激子对的数量，kS为S1态激子辐射复合的速率，kT为T1态激子非辐射复合的速率。曲线拟合时，设定合适的初始值NS(0)、ND(0)、NT(0)和速率值(k-2，k2，k-1，k1，kS，kT)，以0.1 nm 为迭代时间间隔，利用公式(3)进行迭代运算，得到NS(t)，ND(t)和NT(t)随时间的变化，其中NS(t)的衰减即代表薄膜发光强度的变化。拟合结果展示在图3(a)中。类似的，再次基于三步四状态演化模型，可列出如公式(4)所示的耦合的微分方程组来对发光的衰减过程进行描述，其中ND1为1(TT)i态的数量，ND2为1(T…T)态的数量，其他各相关量的设定与方程组(3)相同。再次设定合适的初始值NS(0)、ND(0)、NT(0)和速率值(k-2，k2，kD，kC，k-1，k1，kS，kT)，拟合方法同上，拟合结果展示在图3(b)中。将图3(a)与图3(b)进行对比可以发现，在0～200 ns 的衰减时间范围内，三步四状态模型的拟合结果整体上明显优于两步三状态模型的拟合结果。尽管在初始的100 ns 里，两个模型都能给出符合度很好的拟合结果，但在后续的100 ns 里，利用三步四状态模型算得的拟合曲线明显更符合实验测量结果，而两步三状态模型算得的拟合曲线表现出明显的偏离。上述差异说明，相较于于公式(1)和方程组(3)，公式(2)和方程组(4)对激子裂变过程的描述更加合理，中间过渡态1(T…T)的加入使得演化过程更精细，因而拟合曲线和实验数据的符合更好，这从实验角度证实了1(T…T)态的存在。

图3 不同温度下瞬态发光衰减曲线及其拟合结果

在激子裂变过程中，相互作用的两个分子间通过电荷转移来改变自旋状态。2015 年，Scholes 从理论上描绘了两个分子上在电荷跳转过程中的电子- 空穴排布方式，并计算出了不同排布方式对应的双分子波函数以及两个T1态激子空间分离后的分子波函数。不同的波函数形态具有不同的能量，理论计算的结果表明，耦合形成的双分子态(即前述提到的1(TT)i态)可通过三重态- 三重态能量转移机制(即Dexter 能量转移)，先令两个裂变生成的T1态激子相互远离，但在分子间波函数相互交叠程度下降的过程中仍然保持一定的自旋相互作用，直至波函数交叠完全消失[2]。在2016 年，Pensack 等人分析了激子裂变过程中的瞬态吸收信号的变化，他们指出仅有1(TT)i态是不够的，需要在裂变模型中加入前述的1(T…T)态，他们发现1(T…T)态对应的瞬态吸收信号的谱线形状与1(TT)i态对应的瞬态吸收信号的谱线形状明显不同，而与T1态激子的吸收信号相像。这是因为，在1(TT)i态中两个T1激子之间有较强的相互作用，而在1(T…T)态中这种相互作用由于T1激子空间的分离而大大减弱，这使得裂变分子在电子振动结构部分对应的吸收谱线形状发生变化，这使得两个不同的中间过渡态具有各自的特征因而可以被分别进行追踪[3]。Scholes 与Pensack 等人的分析可以用图4 所示的激子分离示意图来形象的诠释，伴随着两个T1态激子的空间分离，二者间的自旋相互作用逐渐消失。此外，理论研究指出，1(TT)i态与1(T…T)态作为公式(2)中的两个中间过渡状态，速率kD的值明显大于kC的值，说明1(TT)i态的分离表现出某种转化的倾向性。

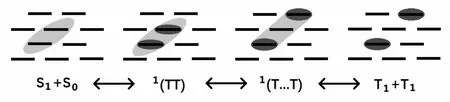
图4 三步四状态演化模型示意图

另一方面，前述提到激子裂变过程是可逆的。经过激子裂变形成的两个孪生的T1态激子，在其自由扩散过程中仍有可能由于碰撞想聚集，进而发生激子聚变过程。就本实验所使用的红荧烯材料而言，当薄膜呈现晶态结构时其载流子迁移率可超过10 cm2V-1s-1，而在一般通过热蒸发方式得到的非晶态红荧烯薄膜中，其载流子迁移率甚至可以低于10-3cm2V-1s-1。较低的载流子迁移率极大的限制了T1态激子的自由扩散距离，造成裂变产生的两个孪生的T1态激子被限制在相邻的几个分子上，所以仍有很大的概率重新结合为1(TT)i态。此外，若化学系统中T1态激子之间相互作用很强，以至于T1态激子对不能实现空间上的快速分离，那么两个T1激子之间就可能只产生具有相互作用的1(TT)i态。在整个的激子演化过程中，从左向右的激子裂变过程和从右向左的激子聚变过程之间是相互竞争的。这种竞争现象在数据拟合过程中体现在公式(2)中的速率拟合数值，其中kD/kC～10，k-1/k1～0.5。通常有机材料中S1态激子的寿命仅为纳秒量级，而T1态激子的寿命可达微秒量级。更多中间过渡态存在的实际效果，类似于储水池的作用，它们保证了激子聚变过程能够持续发生，因而可以不断的产生辐射发光的S1态激子，因而令三步四状态模型对应的发光衰减速度比两步三状态模型对应的发光衰减速度更缓慢。

另外，在处理耦合方程组(3)和(4)时我们进行了简化处理，将1(TT)i态与1(T…T)态自身的衰减都归并到T1态激子最终的非辐射复合过程中。由于本身T1态激子的寿命就比较长，其衰减速率kT通常都比较小，测量结果表明，温度对于T1态激子的寿命并没有太大的影响，尽管温度从300 K 下降到了100 K，5 条衰减曲线的后半段几乎展现出相同的下降趋势。在图3(b)中，300 K 和250 K 温度下的拟合曲线后半段依旧衰减的比较快，这说明温度较高时个状态都会不可避免的存在直接衰减，简化处理方式有可能带来偏差。

3 结论

理论上，基于激子裂变传统的两步三状态模型和新确立的三步四状态模型，在确定了各状态的数量参数和各状态间相互转合的速率参数后，可以分别列出两种模型各自对应的微分方程组。通过数值模拟常用的迭代运算方法，以0.1 nm为迭代时间间隔，可分别计算出0～200 ns 时间范围内不同激发态数量的变化。而实现所测量的薄膜瞬态发光强度的衰减，对应的是其中S1态激子数量的变化。两种演化模型的拟合结果对比显示，通过三步四状态演化模型来描述激子裂变的演变过程要比两步三状态演化模型更合理，同时也从实验角度证实了三步四状态演化模型中过渡态1(T…T)的存在。