一类二阶泛函微分方程正解的存在性
2019-08-30范虹霞
刘 洋, 范虹霞
(兰州交通大学 数理学院, 甘肃 兰州 730070)
时滞微分方程[1]是具有时间滞后特点的微分方程,可以描述当前的和过去一段时间的系统状态。时滞微分方程的研究在近60年来被广泛关注,其中最著名的一个例子是1960年代提出的电动力学中的二体问题[2]。之后,时滞微分方程大量出现在物理学[3]、自动控制[4]、种群增长模型[5]等诸多学科的研究之中。近年来,时滞微分方程解的存在性的研究也获得较多关注,出现了许多关于时滞微分方程周期解的存在性及多解性的结果,在文献[6-10]中都有提及。
Fan等[11]运用锥上的不动点定理研究了二阶非线性常微分方程
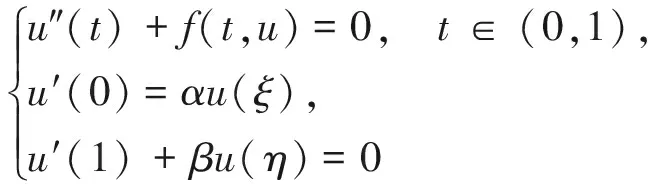
(1)
解正性的缺失。与此同时,有关普通常微分方程边值问题解的存在性研究[12-17]已经日趋完善。而对于Banach空间中依赖于过去时间状态的微分方程边值问题的解的存在性研究较少。受到文献[11]的启发,本文研究带有时滞的二阶泛函微分方程四点边值问题正解的存在性,其中f:[0,1]×Cr→R+是连续函数,对任意固定的r∈R+,Cr表示所有的连续函数
(2)

记Cr,0={ψ∈Cr|ψ(0)=0},则ut在Cr中可定义为
其中φ∈Cr,0。
对固定的ω∈[-r,0],边值问题(2)的一个解u是指u∈C2[0,1],且u满足(2)中的边界条件,并对给定的φ,有
u″(t)+f(t,ut(ω;φ))=0,t∈(0,1)。
本文运用锥上的不动点定理,在-1<ω≤0和-r<ω≤0两种情形下,研究问题(2)正解的存在性。
1 主要假设和结论
下面给出本文要用的假设。
(A1) 1+βη>β;
(A2) 1-αξ>0;

(H2) 存在p1、p2,0≤-ω≤p1 (H3) 存在p1、p2,0≤p1 下面列出本文的主要结果。 对-1<ω≤0有以下存在性结果: 定理1 假设条件(A1)、(A2)及(H1)、(H2)成立,则对给定的φ∈Cr,0,‖φ‖J≤λ,边值问题(2)至少有一个正解u,且满足λ<‖u‖<μ。 对-r<ω≤0有以下存在性结果: 定理2 假设条件(A1)、(A2)及(H1)、(H3)成立,则对给定的φ∈Cr,0,‖φ‖J≤min{λ,μ},边值问题(2)至少有一个正解u,且满足λ<‖u‖<μ。 以下列出本文要用的主要工具。 (ⅰ) ‖Ax‖≤‖x‖,∀x∈K∩∂Ω1, ‖Ax‖≥‖x‖,∀x∈K∩∂Ω2; (ⅱ) ‖Ax‖≤‖x‖,∀x∈K∩∂Ω2, ‖Ax‖≥‖x‖,∀x∈K∩∂Ω1; 引理1[12]设Δ=α(1+βη)+β(1-αξ),则边值问题(2)有唯一的解 其中 引理2 假设条件(A1)、(A2)成立,则对任意的p1、p2且0≤p1 证明由引理1及(A1)、(A2)容易证明 再由(A1)、(A2)可得 所以有 证毕。 为方便起见,记 显然边值问题(2)有一个解u=u(t),当且仅当问题(2)的解u是算子Aφ的不动点。 容易验证Aφ:K→K是全连续的。 下面验证算子Aφ满足定理A中的(ⅰ)。 因此,‖Aφu‖≤‖u‖,u∈∂Ω1∩K。 第二步设Ω2:={u∈K|‖u‖<μ},对u∈∂Ω2,有 从而mμ≤u(t)≤μ,t∈[p1,p2]。此外,对s∈[p1,p2],0≤-ω≤p1 对u∈∂Ω2,这就有‖Aφu‖≥‖u‖。 定理2(证明) 第一步这个问题第一步的证明与定理1的证明类似。 第二步设Ω2:={u∈K|‖u‖<μ},对u∈∂Ω2,有 从而mμ≤u(t)≤μ,t∈[p1,p2]。此外,对s∈[p1,p2],有 即‖us(ω;φ)‖≤μ,因此 对u∈∂Ω2,这就有‖Aφu‖≥‖u‖。 性质P假设f(t,ψ)满足下列条件: 给定p1、p2且0≤p1 (Ⅰ) 若maxf0:=C1∈[0,A),取ε=A-C1,存在λ1>0(λ1可任意的小),使得对任意ψ∈Cr,‖ψ‖J≤λ1,有 因此f(t,ψ)≤A‖ψ‖J≤Aλ1,t∈[0,1],ψ∈Cr,‖ψ‖J∈[0,λ1],则假设条件(H1)成立。 (Ⅳ) 如果maxf∞:=C4∈[0,A),取ε=A-C4>0,存在θ>0(θ可任意的大),使得对任意ψ∈Cr,‖ψ‖J≥θ,有 (3) 现在有下面两种情形。 f(t,ψ)≤L,t∈[0,1],ψ∈Cr, 取λ2=L/A,因此f(t,ψ)≤L=Aλ2,t∈[0,1],ψ∈Cr,‖ψ‖J∈[0,λ2]。 蕴含f(t,ψ)≤f(t0,φ),t∈[0,1],ψ∈Cr,‖ψ‖J∈[0,λ2]。 由λ2≥θ和(3)式,得 f(t,ψ)≤f(t0,φ)≤A‖φ‖J=Aλ2,t∈[0,1],ψ∈Cr,‖ψ‖J∈[0,λ2]。 由情形1和情形2,可知假设条件(H1)成立。 推论1 假设f满足性质P且存在p1、p2,0≤-ω≤p1 可以有相应的结果(ⅰ)和(ⅱ)成立: (ⅰ) 对任意给定的φ∈Cr,0,且‖φ‖J足够小,边值问题(2)有一个正解; (ⅱ) 对任意给定的φ∈Cr,0,边值问题(2)有一个正解。 推论2 假设f满足性质P且存在p1、p2,0≤-ω≤p1 (H7) 存在λ*>0是得f(t,ψ)≤Aλ*,t∈[0,1],ψ∈Cr,‖ψ‖J∈[0,λ*], 则对任意给定的φ∈Cr,0,且‖φ‖J≤λ*,边值问题(2)至少有两个正解u1、u2且0<‖u1‖<λ*<‖u2‖。 证明存在两个实数μ1、μ2满足0<μ2<λ*<μ1, f(t,ψ)≥Bμ1,t∈[p1,p2],ψ∈Cr,‖ψ‖J∈[mμ1,μ1], f(t,ψ)≥Bμ2,t∈[p1,p2],ψ∈Cr,‖ψ‖J∈[mμ2,μ2]。 因此,由定理1对任意给定的φ∈Cr,0,有‖ψ‖J∈[0,λ*],边值问题(2)有两个正解u1、u2使得μ2<‖u1‖<λ*<‖u2‖<μ1,运用两次定理A知算子有两个不动点。2 预备知识





3 主要结论的证明










4 应 用







