对比中现问题碰撞后出灼见——《乘法分配律》一课四个版本教材例题比较研究

朱 军

《乘法分配律》是小学数学运算定律的重要内容，也是小学数学运算定律中的难点。教师在教学《乘法分配律》时，往往会遇到这样的问题：

1.学生很难记忆并理解教材中《乘法分配律》的文字叙述。

2.学生很容易和带括号的乘法结合律混淆。

3.乘法分配律的变式很多，学生很容易在计算中出错。

对此，笔者查阅了沪教版、北师大版、苏教版、人教版教材例题，并尝试对教材中的例题进行分析，旨在获得突破学生学习难点的启示。

一、四个版本例题编排时间的对比与启示

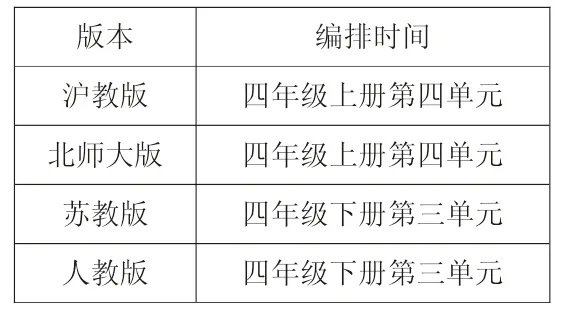
版本 编排时间沪教版 四年级上册第四单元北师大版 四年级上册第四单元苏教版 四年级下册第三单元人教版 四年级下册第三单元

四个版本例题教学都安排在四年级，连单元安排也差不多。原因在于：其一，运算定律和四则运算是一个有机的整体，四年级学生已经基本学完了整数四则运算，如果不安排学习乘法分配律，那么将不利于学生运算能力的提高，而且后续学习小数和分数四则运算以后，乘法分配律仍然适用，甚至在实数、复数乘法中也同样适用，乘法分配律的学习是一个承上启下的关键点。其二，乘法分配律和其他四个运算定律是一个有机的整体，学生对于前面四个运算定律的学习，特别是交换律的理解与应用，基本是水到渠成。如果把乘法分配律单独割裂开来，不利于学生对运算定律有一个完整的认识，所以笔者认为编排在四年级还是比较合适的。

二、四个版本例题情境图的对比与启示

版本 教材情境图 问题呈现沪教版 解决扩建后的长方形的面积问题。images/BZ_60_1537_1530_1907_1723.png北师大版 解决贴瓷砖数量问题。images/BZ_60_1546_1745_1917_1984.png苏教版 解决四、五年级跳绳数量。images/BZ_60_1543_2018_1924_2216.png人教版 解决植树人数问题。images/BZ_60_1543_2254_1921_2633.png

四个版本的教材情境图选择虽然各种各样，但是都贴近生活实际，隐含模型特征。仔细观察，我们可以看出，人教版和苏教版的教材编者选择了领跳绳和植树场景，学生在解决问题的过程中，通过分析数量关系，建立乘法分配律模型。北师大版和沪教版编者选择了贴瓷砖问题和操场扩建后面积问题，让学生在解决问题的过程中，通过数形结合的方式，建立乘法分配律模型。

对比发现，四个版本例题内容选择都是以解决问题的形式出现，其中苏教版选择的跳绳问题比较贴近学生生活实际，容易得出不同解题方法。人教版选择的植树问题，刚好对应当时授课的时间三月初，暗含节日教育意义。北师大版教材选择的贴瓷砖情境，虽然和学生生活实际有点远，但是情境中给学生提供了图示，有利于利用数形结合的方法建立乘法分配律模型，而且问题的解决方法也最丰富，呈现两组四个不同的算式，提供的素材最丰富。沪教版选择的是解决图形面积问题，学生最容易想到通过图示的方法，得出不同的解决方法，能够通过图像很直观地理解乘法分配律的内涵。综上所述，四个版本教材情境呈现各有千秋，但是笔者比较倾向用数形结合的方式帮助学生建立乘法分配律模型。

三、四个版本例题解决方法的对比与启示

版本 解决问题的方法 思路分析沪教版images/BZ_61_446_1307_726_1594.png呈现两种思路，上面的男生先算扩建后操场的宽，再算操场的面积，下面的女生先算操场原来的面积，再算增加的面积，最后算扩建操场的面积，进而得出两种计算方法结果相同。北师大版images/BZ_61_431_1702_755_1920.png呈现两组四种思路，第一组两种方法一个是先分别求出贴好的瓷砖数量和没贴好的瓷砖数量然后再相加，另一个是先求一共有几行瓷砖，再求一共有几块瓷砖；第二组两种方法一个是先分别求出左面的墙瓷砖数量和正面的墙瓷砖数量，再求出一共有几块，另一个是先求出左面和正面的墙一共有几列，再求一共有几块。进而让学生观察，发现两组算式结果相同。苏教版images/BZ_61_425_2040_765_2255.png呈现两种思路，左边的方法是先求出四五年级一共有几个班，再求一共领多少根；右边的方法是先求出四五年级各领多少根，再求一共有多少根，进而得出两种方法结果相等。人教版images/BZ_61_421_2271_763_2588.png呈现两种思路，男生先算每组有几人，再算一共有几人；女生先分别求出挖坑、种树的有几人和抬水、浇树的有几人，再求一共有几人。进而得出两种方法结果相同，还让学生想一想两个数的和在后面的乘法，是否也和分别乘一个数相等。

对比发现：四个版本的教材都是让学生在解决问题的过程中，通过观察不同的解决方法，让学生真实地感悟乘法分配律的存在，继而构建起乘法分配律这样一个运算规律模型。

从解题方法的数量上看，北师大版本教材呈现了四种不同的解题方法，形成了两个等式，提供的算式素材最丰富，其余都是两个算式一个等式。从等式得到的方法上看，北师大版采用半扶半放的方式，通过“观察两组算式，你有什么发现？”这一问题帮助学生得出等式。其余三个版本教材不加任何提示，都是自然得出等式。从等式的形式上看，人教版和沪教版教材都呈现了箭头提示，其余两个版本教材没有；沪教版的等式把两个数的和放在后面，其余三个版本教材都是把两个数的和放在前面，笔者比较倾向有箭头提示的等式，此外乘法分配律的不同变式也应该让学生有所感悟。

四、四个版本例题中概念的呈现与表征的对比与启示

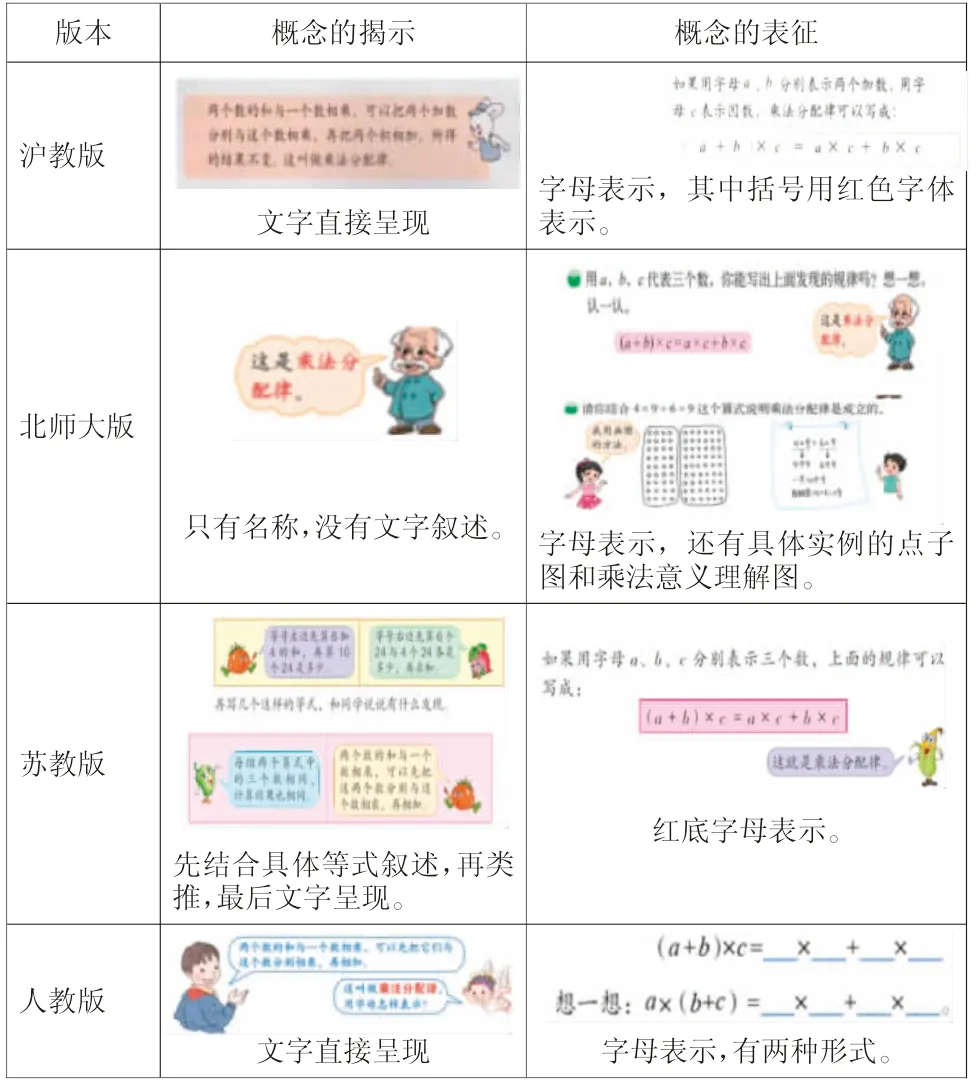
版本 概念的揭示 概念的表征沪教版images/BZ_61_1476_948_1821_1062.pngimages/BZ_61_1958_945_2267_1044.png文字直接呈现字母表示，其中括号用红色字体表示。北师大版images/BZ_61_1532_1195_1759_1314.pngimages/BZ_61_1859_1137_2244_1398.png只有名称，没有文字叙述。 字母表示，还有具体实例的点子图和乘法意义理解图。苏教版images/BZ_61_1480_1491_1809_1703.pngimages/BZ_61_1841_1517_2246_1662.png红底字母表示。先结合具体等式叙述，再类推，最后文字呈现。人教版images/BZ_61_1467_1807_1813_1909.pngimages/BZ_61_1847_1807_2254_1897.png文字直接呈现 字母表示，有两种形式。

对比发现：在概念的揭示上，只有北师大版没有文字叙述，其余三个版本教材都有文字揭示，四个版本教材都非常注重“不完全归纳法”，通过让学生经历“再写几个这样的等式”，运用抽象概括的方法把乘法分配律概念表述出来。在概念的表征上，四个版本教材都有字母形式，而且人教版教材有两种不同的字母表现形式，帮助学生明白乘法分配律的不同变式。北师大版本的教材在概念揭示与表征以后，还安排了具体算式的验证环节，通过画图这种数形结合的方法，以及写几个几这种乘法揭示的方法，进一步巩固对乘法分配律内涵的理解。

不管哪个版本，选择合适的例题呈现方式，运用数形结合的方法和乘法意义归结的方式，采用不完全归纳方法得出乘法分配律，进而通过乘法分配律的不同变式，让学生深化对乘法分配律本质的理解，使学生对这一知识点的学习更上一层楼。