计算错误矫正的几个举措

朱希萍（特级教师）

计算教学很重要,有人将计算与思维并称为“数学的本质”。学生计算的错误无非是心理原因、知识原因、思维原因三方面，关乎于学生的注意力分配不均、注意力不够集中；记忆力不强形成短时信息的丢失；强成分的干扰形成思维定势；知识原理的模糊混淆；技能的不熟练等等。

下面分别从心理、知识、思维三个层面谈谈具体的做法。

一、计算出错的心理原因及对策

1.短时记忆的缺陷造成信息提取失败。

错题例举：

分析原因：学生在计算第二个因数个位上的8和第一个因数十位上的2 相乘时忘了个位相乘进过来的5。

解决对策：手脑并用。

预防信息丢失的方法一是依靠记忆，二是变隐形知识为可视知识。学生记忆力的培养需要一定的过程，因此把隐形知识变成可视知识就显得更为重要。具体做法：哪一位满几十就用左手伸出几个手指头，提醒自己在下一步时加上左手的进位数。实践证明，学生在可视的左手提示下，错误率大大降低。

2.前置学习及注意力不集中的影响。

错题例举1：

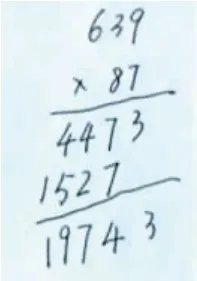
错题例举2（略）：学生在抄题目时会把86 写成68，把“+”号写成“×”号。

分析原因：以上第一题的错误是因为先前学习的加法对乘法造成的干扰，第二题的错误是因为注意力不集中或注意分配能力不强。

解决对策：计算正确率的提高很大一部分取决于学生的习惯，如书写的习惯、审题的习惯、“回头看”的习惯。我们要让学生养成一审、二算、三查的习惯。具体要做到：

要有养成习惯的目标意识。这些习惯的形成需要教师每天放入教学目标，只有教师心中有培养学生习惯的意识，学生的习惯方能形成。

要有习惯培养的干预行为。如在计算乘法题组时放一道加法，在学生想当然时设置一个个例，让学生在不经意间出错，从而形成认真审题的意识。

①3×7=（ ） 21÷7=（ ） 21÷3=（ ）

②6×8=（ ） 48÷6=（ ） 48÷8=（ ）

③7×9=（ ） 63÷7=（ ） 63÷9=（ ）

④56÷7=（ ） （ ）×（ ）=56 56÷（ ）=7

⑤8×5=（ ） 40+5 =（ ） 40+8=（ ）

⑥7×7=（ ） 49÷（）=（）

前四组都是根据一句口诀应用的乘除法算式，第⑤题是一道乘法和两道加法，主要训练学生看清运算符号的意识。

二、计算出错的知识原因及对策

1.知识原理没有理解。

错题例举：

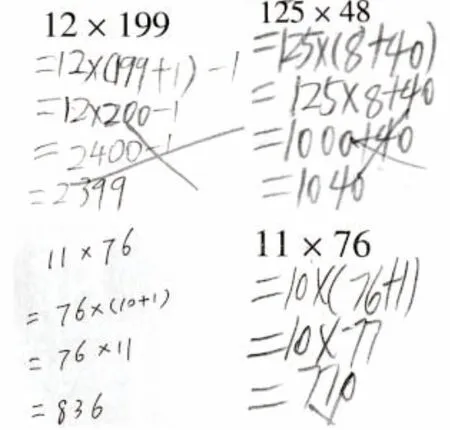
分析原因：学生对运算律的理解只是掌握了它的“形”而没有理解“神”。没有真正掌握乘法分配律的内涵，知识的运用存在着盲目性。

2.知识原理相混淆。

错题例举：

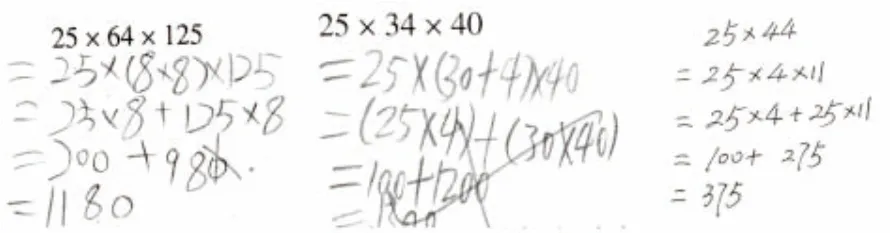
分析原因：学生将乘法分配律和乘法结合律知识搞混淆了。

解决对策：借助情境帮助学生从意义上理解知识的本质，建立数学模型。

教学中让学生在具体情境中抽象出数学模型——利用情境初步理解原理——借用乘法意义深刻理解模型本质——数形结合加固建立数学模型。

具体教学如下：

呈现如下问题情境：

常规教学教师会让学生用不同的方法解决以上问题，抽象出乘法分配律的数学模型，然后举例验证（包括举正例与反例），最后归纳总结，应用规律。

这样的教学让学生经历了对“乘法分配律”的观察、归纳、举例验证的全过程。可有些学生还是没理解透。这时我就引导学生从不同的角度来阐述规律存在的理由。

例如（40+8）×125=125×40+125×8，有人说表示125 套服装,可以先算一套服装的价钱再算125 套服装的价钱，也可以先算上衣的总钱数再加裤子的总钱数。有人说40 加8 的和乘以125 可以是40 个125 再加8 个125。

125×40＋125×8=125×（40+8）表示先算125 件上衣的价钱，再加125 条裤子的价钱；也表示40 个125 加8 个125 就是40 加8 个125 即48 个125。

而125×48=125×8×6 表示125 的48 倍，可以表示成125 的8 倍的6 倍。

用图形形象地来表示125×（40+8）、125×8×6 与125×（6+8）区别。

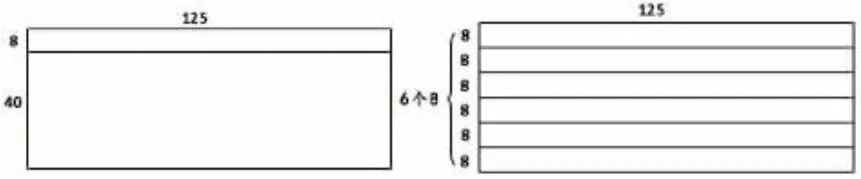
这样从意义本身来理解，就能清楚地区分乘法结合律和乘法分配律的知识。再用数形结合加深对模型的理解，达到纠错的效果。

三、计算出错的思维原因及对策

1.数字信息的干扰。

错题例举：

9×9－9=9×0=0

6400÷25×4=6400÷（25×4）=6400÷100=64。

2.运算律的干扰。

3.运算符号的干扰。

分析原因：学生在计算时思维定势的干扰主要表现在数据的干扰、运算符号的干扰和运算律的干扰。

解决对策：加强对比中分析错因，掌握正确方法，再强化训练。这种强化可以通过题组训练，比较沟通。可以出示类似如下的题组：

（1）计算题组一。

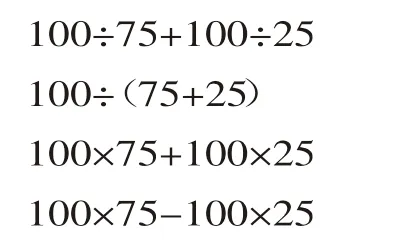
（2）计算下面三个题组。

（3）先说说下面各题怎么算，再分别改一个数据，或改一个运算符号，使计算更简便。

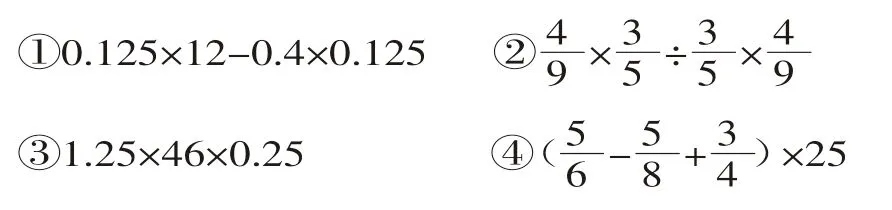
（4）编题：从下面各数中选出一些数，再从“+、-、×、÷、（）”中选出一些运算符号，编出能简便计算的算式，再试着编一些容易错用运算定律和性质的算式。

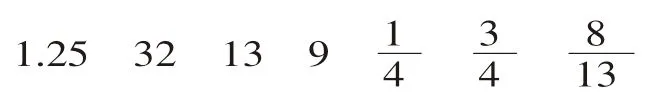
将易错的题以题组出现，通过比较辨析达到正确理解。紧接着通过改变一个数字或运算符号使简便计算凸显出重点：要关注数字特点、符号特点及遵循运算律。