层层递进：叩响速度意义之门——《速度、时间和路程》教学思考与实践

黄 建

《速度、时间和路程》是浙教版三年级下册第一单元的内容。这是学生在学习了单价、数量和总价后进行的教学，教材在下一节安排进一步学习工作效率、工作时间和工作总量。统观三节课，从数量关系上讲，都涉及了份总关系，是份总关系在不同生活情境中的具体化。从教学架构上讲，都从对“每份数”（单价、速度、工作效率）的概念理解切入，既解释了每份数的情境含义，又建构了求每份数的计算方法。

【教学过程】

一、创设情境，感知速度

1.时间相同，路程不同。

（1）出示规则，解读规则。

师：狐狸说自己是动物城里跑得最快的动物，为了证明，它决定和兔子来一场比赛。它制定了这样的规则：都跑4 分钟，看谁跑得比较快。

师：看懂了吗？能比出谁快吗？怎么想的？

生：可以比出来。它们都跑了4 分钟，谁跑得远，谁就赢了。

（2）情境模拟，比快慢。

师：（动画演示）现在，能说出谁跑得快吗？理由是什么？你能对狐狸说说看吗？

生：狐狸啊，狐狸！你看，你跟兔子都跑了4 分钟，你只跑了240 米，兔子却跑了280 米，你不如它快。

生：狐狸啊，狐狸！你看，你们都跑了4 分钟，兔子比你多跑了40 米，你别吹牛了！

（3）小结：时间相同，可以比路程，路程长的，跑得比较快！

2.路程相同，时间不同。

（1）改变规则，解读规则。

师：不服输的狐狸又找来了牛警官，再战一回。这次他偷偷地改了一下规则。请看：都跑240米，看看谁跑得比较快。

师：看懂了吗？能比出谁快吗？怎么想的？

生：当然可以比出来，都跑240 米，谁时间用得长谁就赢了。

生：不对，谁用的时间短谁就赢了，跟我们50 米跑步一样。

（2）情境模拟，再比较。

师：（动画演示）同学们！现在能比出快慢吗？跟狐狸讲话要有理由哦！

生：狐狸啊，狐狸！你看你跟牛警官都跑了240 米，它只用了3 分钟，你却用了4 分钟。它用的时间比你的短，它比较快！

（3）小结：路程相同，比时间。时间短的，跑得比较快！

3.时间和路程都不相同。

师：两场比试过去了，狐狸输得心服口服。第一场比赛，时间相同，比路程。第二场比赛，路程相同，比时间。狐狸心中还有一个疑问，兔子和牛警官时间、路程都不相同，怎么比？

【设计意图：创设动物城赛跑的情境，一方面是动物城的故事学生比较喜欢，有一种积极的情感导向；另一方面，能快速激活学生关于“跑得快”的经验，支持学生开展“速度、时间、路程”的数学讨论。具体又分成三个小问题：1.时间相同，路程长，比较快；2.路程相同，时间短，比较快；3.路程时间都不相同怎么办？自然引入新课。使用“狐狸啊，狐狸！你看”这样的语言来说理，起到进一步渲染情境的作用，同时，在这个过程中关注学生表达的数学化：什么相同，比什么，为进一步理解速度的意义奠定基础。】

二、问题引领，建构模型

1.比一比，谁比较快。

师：请你把想法在作业本上写一写。

?时间（分钟） 路程（米）兔子 4 280牛警官 3 240

独立思考：什么相同？比什么？你是怎么样让它们一样的？

（1）求出1 分钟的路程。

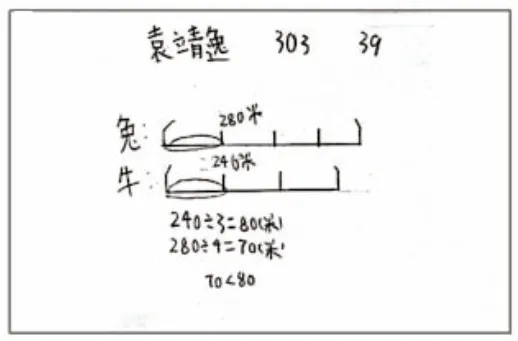
生：我先用280÷4=70（米），算出兔子1 分钟跑了70 米。然后240÷3=80（米），算出牛警官1分钟跑了80 米。因为：80＞70，所以牛警官比较快。

生：他是把牛警官和兔子的时间变得一样，来比较路程。

（2）画图比较。

生：我跟他的想法一样。但是，我还画了一幅图。一共是280米，用了4 分钟，我就把它平均分成四份，一份就是它1 分钟跑的路程。比较一份就可以了。

生：你跟上面的方法是一样的，都是把时间变成1 分钟，然后比路程。

师：他不仅能读懂这幅图的含义，还能和刚才的作比较，能听明白吗？

2.数形结合认识速度。

（1）出示图形。

师：为了把这个过程表示得更清楚，黄老师把它放大，你能读懂吗？

生：兔子4 分钟跑了280 米，这个280 米就是它的路程，说明兔子1 分钟跑了70 米；牛警官3分钟跑了240 米，说明牛警官1分钟跑了80 米。其实，我们比较的就是这样的一份。

（2）理解速度的意义。

师：70 表示什么？

生：是路程。

生：不是的！这个70 米是兔子1 分钟的路程。

师：看来70 不但是路程还隐藏着1 分钟。同样的道理，这个80 呢？

（3）认识速度。

师：像这样每分、每秒、每时，单位时间行的路程就叫做速度。因此，这里的70 其实就是速度。这样写可以吗？（板书：70 米）

生：我们知道，这里的70 表示1 分钟走的米数，你只表示了路程，没有表示时间。

生：是啊！要把速度的两个意思都表示出来。

生：我知道怎么表示：70 米/分。读作：70 米每分。就表示每分跑了70 米。

（4）借助图形得出数量关系式。

师：刚才我们认识了速度，那你觉得速度怎么求？能不能结合上幅图来说一说？

生：速度=路程÷时间。

生：路程就是总的长度，时间就是有几份，速度就相当于每一份是多少。我们知道每份数等于总数除以份数，所以速度就等于路程除以时间。

3.借助速度，比快慢。

（1）其他方法。

师：除了像刚才这样比速度还有其他方法吗？

生：牛警官的速度是240÷3=80（米/ 分），假设牛警官也跑了4 分钟，就跑了80×4=320（米），只要比较320 米和280 米就可以了。所以牛警官比较快，大家有疑问吗？

生：他是先算出牛警官的速度，再把牛警官和兔子的时间变得一样都是4 分钟，比路程。

生：是的！还可以把两人的时间都变成3 分钟，再来比路程。

（2）观察对比。

师：请你仔细对比这几种方法，它们有什么相同的地方？

生：都是把时间变得一样，直接比较路程的长短，就能比出快慢！第一位同学是把时间变成1分钟，第二位同学把时间都变成3 分钟或4 分钟，再比路程。

生：那我们能不能把路程变得一样，来比较时间呢？

生：当然可以！其实当路程和时间都不相同的时候。我们把一个量变得一样，比较另一个量就可以了。

4.总结提升。

生：原来速度就藏在比快慢中啊！时间、路程都不一样的时候，我们把它们的时间都变得一样，如1 分钟、1 小时，再比路程。

生：速度就是1 秒钟、1 分钟、1 小时走的路程。

【设计意图：在此环节中学生进一步思考：路程、时间都不相同，如何比较快慢？这个环节中，有了充足的思考时间与空间作保障，学生的想法也精彩纷呈。第一类想法是将时间变得一样，比较路程。而在时间的选择上也各不相同：1 分钟、3 分钟、4 分钟甚至是12 分钟。原来速度就隐藏其中，1 秒钟、1 分钟、1 小时走的路程就叫做速度。第二类想法是将路程变得一样，比较时间。在这个探究过程中，画图方法的出现将抽象的速度具体形象化。一方面它赋予了速度意义，它不仅代表路程，而且代表了1 分钟走的路程，使得复合单位（米/分）的出现顺理成章；另一方面，学生借助图进一步理解数量关系的意义：路程相当于总数、时间相当于份数、速度相当于每份数，数量关系的出现也变得自然而然。】

三、联系生活，拓展延伸

活动一：数量关系的建构。

（1）读出数感。

师：蜗牛的爬行速度约为9 米/小时。读一读，并且说一说是什么意思。

（2）思考。

①蜗牛12 小时爬行多少米？

②蜗牛爬行63 米，需要多少小时？

（3）全班交流。

出示数量关系式：路程= 速度×时间，时间=路程÷速度。

活动二：速度意义的再理解。

师：如果组织一场人豹PK赛，你觉得谁更快？有没有依据？

生：1 分钟是60 秒，9×60=540（米/ 分），1800 米/ 分＞540米/分，所以豹子快。

生：我还有一种方法，1800÷60=30（米/秒），30 米/秒＞9 米/秒，所以豹子快。

师：都是速度，为什么不能直接比？

生：虽然都是速度，但是时间不一样。一个是1 分钟，一个是1秒钟。我们需要把时间变得一样才能比较。

生：我还有一种方法。豹子1分钟跑了1800 米，刘翔1 秒钟跑了9 米，如果刘翔也跑1800 米，那么他需要1800÷9=200（秒），200 秒是3 分钟还多，豹子只用了1 分钟，所以豹子快。

生：我知道你是怎么想的！你是把它们的路程都变成1800 米来比时间，时间短就比较快。这种方法肯定可以。

活动三：综合练习。

（1）出示信息，填表。

（2）仔细观察，你有什么发现？

生：速度越来越快，时间就越来越少。

生：速度乘2，时间就除以2，总路程不变。

师：关于速度、时间、路程这样的关系，我们以后还会继续研究。

【设计意图：这个环节，我们共分成了三个活动。活动一：读速度、说意义，得出数量关系式；活动二：感知速度、比快慢，深入理解意义；活动三：用速度，感知速度、时间与路程的变化，为今后学习比例奠定基础。】

【教学反思】

这节课，我们始终围绕着比快慢展开教学，但是比快慢不等于速度。比快慢是一个生活中学生常常接触到的情境，如：在50米跑步中，A 小朋友用了8 秒，B小朋友用了9 秒，于是我们说A小朋友跑得快，速度快。那什么是跑得快呢？只是时间用得少吗？当然，它不是速度，却蕴含了速度。

因此，速度的产生是这节课中一根重要的“线”。在第一环节，用时间相同比路程，路程相同比时间这样的方法就开始埋下伏笔。第二环节中，当时间和路程都不相同，怎么比较？时间和路程都不相同时，学生想到了把其中一个量变得相同比较另外一个量即可。时间变得相同比路程：时间可以都转化成1 分钟、3 分钟、4 分钟、12 分钟等，这时只要比较路程即可。而这个过程中，把时间转化成1 秒钟、1 分钟、1 小时，单位时间走的路程就是速度。

对于速度的意义理解更加深刻。首先，学生发现速度是一个“复合”的量，这个量同时表达了时间（单位时间）和路程。借助下图，学生进一步理解它的意义。“速度”的优点就在于一份的量既表达了路程（70 米），又表达了时间（1 分钟），两者同时被表达。其次，这幅图也有助于数量关系式的建构，学生得出数量关系式也有了依据。速度就是这样的每一份，相当于求每份数（体现了浙教版教材关注的结构化思想）。因此学生不仅理解了速度这个复合量代表了两个量，还感知了速度、时间和路程之间的关系，这让教学从速度的产生到数形的结合都始终围绕速度的意义。

练习的设计也是围绕速度的意义展开。通过读，理解速度的意义：9 米/ 秒，表示1 秒跑了9米。原来，速度的单位名称中也有速度意义的理解。通过思考9 米/秒和1800 米/分都是速度为什么不能直接比较这个问题，学生还是围绕速度意义的理解，发现它们的时间不一样，不能比较。这时学生透过抽象的数，看到了速度的本质。最后，当路程相同时，速度和时间的变化规律为六年级进一步学习正反比例埋下伏笔。