化零为整重塑元认知——《分数初步认识整理和复习》教学与思考

叶 青 周 婕

小学数学的“整理与复习”课是对一个阶段所学的知识进行归纳整理，有查漏补缺并让知识在学生脑海里条理化、系统化的作用。它对学生系统掌握知识、发展思维能力极为重要，同时也是教师弥补教学中的遗漏，提高教学质量不可缺少的重要环节。

“整理与复习”课的常规模式是让学生自主梳理一个单元的知识，然后以“知识网络图（思维导图）”的模式进行呈现。在此基础上教师与学生对知识进行分类巩固及练习。基于这样的认识，我校教研组在研磨三年级上册第八单元《“分数初步认识”的整理与复习》一课时最先也采用了这样的教学模式。但在试教时却发现，学生对于本单元所学的知识虽能如数家珍般一一道出，但都只是点到即止，“思维导图”成了一种形式，借助“思维导图”梳理单元知识这一环节最后被演变为展示学生绘画水平、语言表达能力的个人才艺秀。究其原因主要有两点：第一，教师在组织和引导学生进行知识整理时，采用“放羊式”教学。表面上，“放羊式”体现了教学的开放性和学生的自主性，实际上多数学生在整理的过程中不知所措、浅尝辄止。这种教学方式导致学生对知识的梳理只关注表面，没有结合自己的学习实际挖掘这单元学习中重难点和易错点。第二，三年级的学生以具体形象思维为主，对于“分数”这种比较抽象的数的认识需要借助具体情境加以理解，脱离了情境的知识整理反而增加了学生理解上的难度，导致复习过程散乱无趣，学习缺乏核心源动力。

“思维导图”的整理在整理与复习课中是否就没必要存在了呢？我认为还是有必要的。关键在于如何引导学生进行整理，把散状的知识串联起来，做到形散神不散。如何充分发挥该图的最大复习功效帮助学生重塑元认知？下面结合教研组研磨的《分数初步认识整理与复习》一课中的教学片断谈谈自己的点滴思考。

片断一：情境引入，汇集认知元素。

师：（课件演示）这是一个旅游景点的俯视图，仿古建筑与公园各占了一半的面积，公园由树林和湖组成。根据俯视图制成一张公园平面图。从平面图上你能找到仿古建筑区和公园区吗？

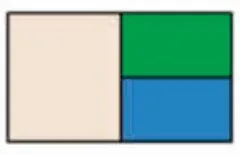
学生辨认后布置学习任务：

1. 在图中你能找到哪些分数？向同桌进行介绍。

2.说说每一个分数所表示的意义。

师：从图中找到了这么多分数，能联想到哪些分数知识呢？

生：我会读这些分数，也知道每一个分数由一条分数线、分子和分母组成。分数线上面的数是分子，下面的是分母。

生：我会比较这些分数的大小。

生：我还知道这些分数表示的意义。

生：我还能进行计算。

师：读写分数、分数的意义、大小比较、计算都是本单元学习的内容。

【思考：本节课是学生第一次接触分数，也是学生认识数的概念的一次质的飞跃。本单元的学习目标是借助实物、图形，直观认识几分之一、几分之几。课伊始，以景点平面图引入让学生运用学过的知识寻找分数，旨在激活学生头脑中对于分数的元认知，进而道出诸多的分数知识，为后续知识的整理和复习提供了原始素材，可谓一举两得。】

片断二：对比整理，复习分数意义。

1．同一分数对比，巩固意义。

师：这两位同学都是把整个景点平均分成两份，表示其中的一份。

生：我是把整个公园平均分成两份，树林和湖分别是整个公园的二分之一。

师：同样都是二分之一，我们发现它们表示的意义各不相同。

2．不同分数对比，深化意义。

师：图上明明只有三份呀，你是怎么看出平均分成四份的？

生： 我们可以把仿古建筑区也平均分成两份。

生：树林也占了整个景点的四分之一。

生：把旅游景点平均分成四份，公园占整个景点的四分之二。

师：刚才的公园是整个景点的二分之一，现在怎么又成了四分之二？

生：刚才是把旅游景点平均分成两份，现在是平均分成四份。

师：同一个面积，平均分的份数不一样，表示的分数也不一样。

生：把旅游景点平均分成四份，仿古建筑和湖共占了它的四分之三。

生：把旅游景点看成一份，取其中的一份，就是一分之一。

生：可以。

师：像一分之一、二分之二、四分之四这些分数都表示单位“1”。

师：从图中我们找了这么多不同的分数，那什么是分数？

（引导学生回顾梳理：把一个物体平均分成几份，一份就是几分之一，几份是几分之几）

【思考：利用学生自主发现的分数作为学习素材，通过对同一个分数表示不同的意义，不同的分数表示同一物体的辨析，在相同与不同中的思辨，帮助学生建构分数意义的本质。“”的出现也是教师因势利导渗透分数单位“1”的有利契机，为五年级继续学习分数做好铺垫。】

片断三：归类分组，比较分数大小。

1.分子相同进行比较。

师：你是怎样想的？

生：两个分数的分子相同时看分母，分母越大分数反而越小。

师：比较同分子分数的大小，方法多种多样，从不同的角度去思考，就会得到不同的方法。最终我们发现分子相同，分母大的分数反而小。

2.分母相同进行比较。

生：也可以看平面图中这些分数所表示的面积来比较大小。

生：分母相同时，分子越大分数就越大。

师：在这些分数中，你们能找到相等的两个分数吗？

师：你的理由是什么？

生：二分之一表示为景点的一半，比如仿古建筑；四分之二也表示景点的一半，所以它们是相等的。

师：太棒了，你们运用分数的意义来进行比较解决了五年级要学的知识。虽然我们还没有学过通分，但是我们可以想办法把这些没有学过的知识转化为已经学过的知识，用这种办法解决问题。

【思考：教师尊重学生，以学定教，顺着学生的思维生成，在课堂中通过追问“你能把这五个分数（）分分类吗？”引出“分子相同”和“分母相同”两种情况，借机对分数比较的方法进行复习。同时渗透转化思想，借助分数的意义比较同分子分数的大小，拓展了学生的思维能力。课堂教学关注数学思想，将其蕴涵在数学知识形成、发展和应用的过程中，使数学知识和方法在更高层次上得以抽象和概括。】

片断四：分析前测，回顾巩固认知。

（课件呈现前测内容）

师：知道哪一题错误率最高吗？你是怎么知道的？

生：第1 题错得最多。

师：这道题为什么是错呢？

生：没有提到“平均分”。

师：是呀，分数是建立在“平均分”基础上得出的一类数。

【思考：前测，有助于教师把握学情，抓住错例，突破教学重难点。此片断的设计既是对易错题的分析、加深了学生对于“平均分”在分数认知中的重要性，又把错误以分数的形式呈现，成为分数比较练习的素材。可谓一题多用，巧妙地发挥了前测的作用。】

片断五：情境再现，发展综合能力。

师：旅游景点需要建造一个停车场，于是整个景区规划成这样三部分。

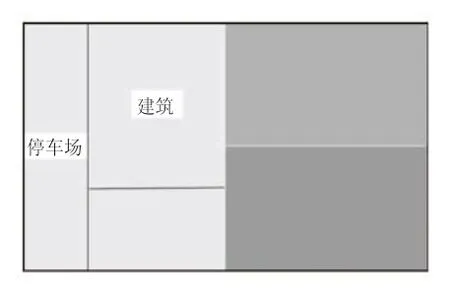
师：你能估计一下建筑区大约占了这个景点的几分之几？停车场呢？

生：我估计建筑区占了九分之四，停车场占了九分之三。

师：看着这幅图，你还能提出什么数学问题？

生：停车场与建筑区共占了几分之几？

生：建筑区比停车场多占了几分之几？

生：景区还剩几分之几没有被开发？

师：这些问题你们会解决吗？

（学生列式计算，全班总结分数加减法的计算方法。板书：分母不变，分子相加减）

【思考：在该教学片断中，教师不仅结合具体的问题情境让学生进行估计，培养数感，让学生体会到估算的意义和价值。还让学生根据情境提出问题，独立解决，在学生汇报时，引导学生分析问题，从而提高学生的问题意识，培养学生解决问题的能力。】

【教学反思】

本课是一节单元整理与复习课，但不是机械重复的练习课，而是希望通过知识的重新组合，促进学生的认知发展。

一、唤醒元认知，再现知识

本课的“知识网络图”不是安排在课的一开始就进行整理，而是贯穿在整节课的学习过程中，当课结束时，“知识网络图”也自然形成了，学习的无痕教育就体现于此。把“旅游景点平面图”作为本节课的主要学习素材，教师通过一个又一个环环相扣的问题，逐一唤醒学生脑海中的元认知，引导他们对整个单元的知识点进行梳理。大情境大问题的设计，让零碎的知识自然呈现，并在一个个问题的解决中使学生回顾知识总结方法。整个学习过程渗透了“观察、发现、分类、转化”等思想方法，有助于学生更好地理解每一个知识点背后其所蕴含的意义、思想和方法。

二、建构元认知，整理知识

在“分数初步认识”的复习过程中，一方面依然以旅游景点平面图为支架，沟通学生已有的分数认知和储备，借助数形结合的方法来理解分数的含义，把零散的知识点（分数名称、含义、大小等）作比较系统的梳理；另一方面，以核心问题为引导，通过分享、合作和交流，很好地把同分母分数、同分子分数的大小进行比较，又能通过分数的意义拓展分子分母都不同的分数大小比较的方法，使学生在实际问题的解决中感悟方法，提升知识整理和复习的自主能力，最终在脑海中建构完整的知识体系，为今后的分数再学习做好铺垫。促进学生自主梳理本单元的知识，形成“知识网络图”。

三、实践新认知，应用知识

“整理与复习课”教学的关键是要了解哪些是学生已经熟练掌握的，哪些是学生理解运用起来比较困难的。通过前测，可以深入地了解学情，从而确定复习的重、难点。根据前测的结果分析，并将通过分析的前测素材引入课堂教学，极大地丰富了教学资源。本节课把前测的内容安排在全课整体的回顾及整理之后，再对前测结果进行分析，有助于学生更好地应用知识。对于错误率比较高的题目，以判断题的形式出现，统计的结果也不是常规的百分数形式，而是用分数表示，问：“你看得懂这几个分数吗？哪一题错的人最多？”此设计将分数真正应用到了生活实际中，学生兴致高涨。同时让学生初步感知了分数不仅可以表示“部分与整体之间的关系”，还可以表示“分率”，对分数的意义有了新的认知。

寻找学生学习的知识散点，摸索学习的认知规律，形成知识体系是整理与复习课的目标，会做题目并不是目的，关键在于通过整理和复习，帮助学生将碎片化的知识形成一个知识整体，并能在整理与复习过程中，弥补学习之短板，拓展学习的能力。