探深度理解之妙法寻破解难点之策略——“求比一个数多（少）几的数”教学难点突破的实践与思考

蓝海鹏

每一节数学课，都有明确的教学目标。在一节课的教学目标中，总存在着教学的重点和难点。通常，教师对一节课的设计与组织基本上不会有太多困难，而难就难在如何创新，如何把课上得深入透彻，让学生易懂易学。而要做到这一点，最重要的就是采用怎样的策略突破难点。

“求比一个数多（少）几的数”属于一步加减计算问题，教材编排时，把这种运算放在问题解决即放在情境中学习。它是学习两步加减计算及应用问题的基础，更是后续学习四则运算的基础。“求比一个数多（少）几的数”这一知识点教学的重点是分析数量关系，确定运算模型；难点是对“…比…多（少）”意义的理解。解决了“…比…多（少）”意义的理解，所有问题就都迎刃而解了。

笔者曾经就加减两步计算应用问题设计了两道题“某校三（1）班有男生25 人，女生比男生多5 人，该班共有学生多少人。”“某校三（1）班有男生25 人，比女生少5 人，该班共有学生多少人。”进行调研，选择连南县城三所学校二年级各两个班共计240 人进行后测。调研发现，学生在“多”“共”等关键字词上方写上“+”号，在“少”字上方写上“-”号。测试结果显示，“男生25 人，女生比男生多5 人”，求女生人数列式正确率为71.9%。而“男生25 人，比女生少5 人”，求女生人数列式正确率仅为8.5%，54.2%的学生列出“25-5=20”的错解式。有的把“比女生少5 人”看成是“女生少5 人”，或认为是女生人数是5 人。由此可见，出错学生并没有弄懂“…比…多（少）”所表达的意思，没有弄清楚关键句中谁是标准量、谁是比较量及谁大谁小。这说明“求比一个数多（少）几的数”的教学出现了问题。

为了有效突破“求比一个数多（少）几的数”教学难点，笔者采用了以下策略。

突破策略一：问题组引导+题组串联策略

【问题组引导】目的是把“…比…多（少）”的含义像剥竹笋那样，一层一层地把外壳剥去，让内在的笋肉、笋心显露出来。

下面以“（1）笑笑养了26 只鸭，养的鸡比鸭多11 只，鸡有多少只？”教学为例，谈谈“问题组引导”策略的运用。

问题1：你是怎样列式的？怎么想的？

（让学生初步说一说）

问题2：哪句是关键句？谁和谁比？谁是较大数？谁是较小数？

（引导学生审题，用自己的方式分析数量关系）

学生尝试在题目的关键处画一画、圈一圈。如在关键句“鸡比鸭多11 只”的鸡和鸭字处画方框或画圈，在“多”字下面画着重号，然后在鸡字下面写上“较大数”或“大”，在鸭字下面写上“较小数”或“小”。通过这样的方式，引导学生聚焦重点，从题中抽象出数量关系。

问题3：题目要求的是较大数还是较小数？用什么方法求？

比如第（1）题，根据“26 只鸭”“鸡比鸭多11只”，或根据“鸡有多少只”，明确题目要求的是较大数：鸡的数量。在学生思考、讨论和交流的基础上，归纳出方法：求较大数要用加法。这里分析数量关系采用非常简洁的方法，避免用复杂分析可能给学生带来理解上的困难。

【题组串联】在对上面问题深入教学的基础上，对该题进行变式，形成题组。变式题组及关系如下：

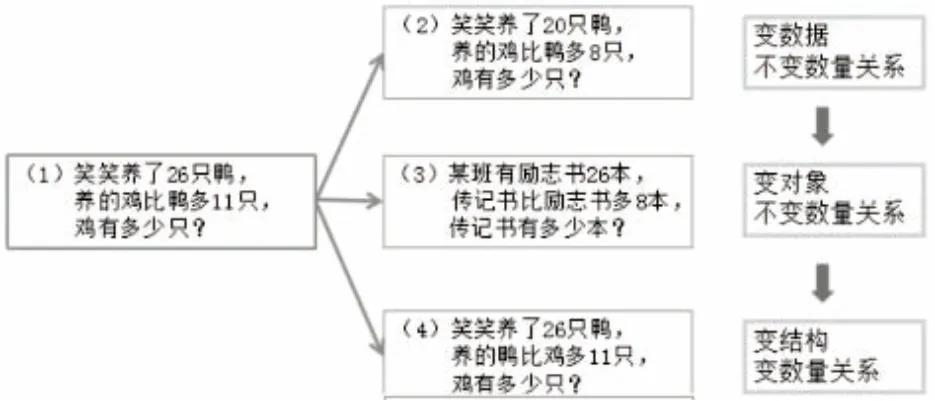
题组串联，从“求比一个数多几的数”的一道典型题出发进行变式，一是变数据而不变数量关系，二是变对象而不变数量关系，三是变结构变数量关系。一变再变，不断激活学生思维，在变式情境中，充分感受、深刻理解“…比…多（少）”的含义。学生按照同样的思路独立解决（2）（3）（4）题，并归纳总结出求较大数和求较小数分别采用的方法。最后思考：变了什么？数量关系变了没有？在独立思考、交流讨论中明晰，其区别是物体不同或者数据不同。其联系是数量关系相同，方法相同，即求较大数用加法，求较小数用减法。

经历了以上教学，然后再把上面的题组中的“…比…多”改为“…比…少”形成新的题组，让学生尝试解决，独立总结，对比交流，集体建构。

问题组引导强调的是，一道题中如何理解“…比…多（少）”的意义，总结出方法，建立一步计算问题的认知。题组串联强调的是，多道题中如何理解“…比…多（少）”的意义，验证方法，构建完整的认知体系。

突破策略二：多种方式表征意义

对于“笑笑扎了6 朵红花，笑笑比淘气多扎4 朵，淘气扎了多少朵?”这个问题，难点是理解“笑笑比淘气多扎4 朵”的含义。在正确分析数量关系基础上，选择加法或减法进行计算。如何突破这个难点呢？

下面以笑笑和淘气有红花的情境为主题，设计以下表征方式。

方式1：用实物图呈现题目。

（1）笑笑有__朵，淘气有__朵。 ____ 多，____少。

（2）笑笑比淘气 ____2 朵，淘气比笑笑 ____ 2朵。（填“多”或“少”）

方式2：用实物替代图呈现题目。

笑笑：○○○○○○ 淘气：○○○○

（1）笑笑有__朵，淘气有__朵。 ____ 多，____少。

（2）笑笑比淘气 ___ 2 朵，淘气比笑笑 ___ 2 朵。（填“多”或“少”）

方式3：用文字呈现题目。

笑笑有8 朵，（1）淘气比笑笑多3 朵，则淘气有____朵；（2）淘气比笑笑少3 朵，则淘气有 ___ 朵。

方式4：用文字呈现题目。

已知笑笑比淘气多3 朵，（1）如果笑笑有6 朵，则淘气有 ____ 朵；（2）如果笑笑有5 朵，则淘气有____朵；（3）如果笑笑有4 朵，则淘气有 ____ 朵。

方式5：用表格呈现题目。

?

方式1 和方式2，先给出两个对象的具体数量，要求学生回答谁大谁小，弄清楚谁比谁多（少），并用文字表达出来。方式3～5，给出一个对象的具体数量和两个对象的大小关系，求另一个对象的数量。前者是“已知两个对象的具体数量→用‘…比…多（少）’语言表述两个对象的关系”，后者是“已知用‘…比…多（少）’语言表述两个对象的关系，其中一个量→求另一个量”。通过以上五种方式，有效帮助学生深度理解“笑笑比淘气多扎4 朵”的含义。

接着，跳出刚才的情境，采用其他方式，设计表征方式。

方式6：用具体数字。

10 比4__6，4 比10__6。请举其他例子。

方式7：用图示表示数。

已知，如图□□□□□□□□○○○○

（1）□ ___ ，○ ___ 。（填“多”或“少”）

（2）□比○ ___ ，○比□ ___ 。（填“多”或“少”）

方式8：用字母表示数。

（1）A 比B 大2，则A___，B____。（填“大”或“小”）

列式为：___+ ___ = ___或 ___ - ___ = ___。（填“A”或“B”或“2”）

___+2= ___ 或 ___ -2= ___ 。（填“A”或“B”）

（2）C 比D 小3，则C ___ D ___ 。（填“大”或“小”）

求C 的方法：D ___ 3。（填“+”或“-”）

求D 的方法：C ___ 3。（填“+”或“-”）

以上设计，旨在让学生在丰富的学习中，从关键句中正确领会“谁大”“谁小”，找到大与小、多与少之间的关系，明晰用加法或是用减法来解决问题。这样教学，让学生充分经历从“图式表征→表格表征→文字解释→列式表征”不同呈现方式表征题意及理解的过程，经历从“数字→图（□○）→字母→规律方法”的符号化过程。

“求比一个数多（少）几的数”的教学难点突破策略有很多，以上所说的突破仅仅是其中的有效策略之一。好的策略总是根据学生实际情况精心探寻出来的。只要是好的策略，一定会通过学生的学习效果得以检验。在每一节课的教学中，都需要教师精心设计突破难点的学习过程，这是教学创造的过程，也是促进学生发展核心素养、发展创新能力的过程。