一类Lipschitz非线性时滞离散广义系统降维观测器的设计
2019-08-28
(1.沈阳工学院基础课部, 辽宁抚顺113122; 2.辽宁石油化工大学理学院, 辽宁抚顺113001)
0 引言
近几年,非线性系统状态观测器的研究非常活跃,非线性系统状态观测器分为全维观测器和降维观测器两种,其中降维观测器只能估计与系统的输出状态无关的部分状态向量,它的维数要比全维观测器低,可用较少的变量表示且整个控制系统更简单[1]。针对非线性系统观测器的研究方法一般可归为两类:一是坐标变换法;二是类Lyapunov方法。第二种方法几乎在各种情形下的观测器设计中得到广泛的应用,其基本思想是基于Lyapunov稳定性理论[2]。
针对含有Lipschitz非线性部分的系统观测器设计,文献[3-5]分别进行了研究。文献[1]利用微分中值定理和Schur补研究了一类离散时间非线性系统降维观测器设计问题。文献[6-7]借助于线性矩阵不等式以及微分中值定理,讨论了一类非线性系统的降维观测器设计问题,给出了一类非线性系统降维观测器存在的充分条件。文献[8]基于输出对未知输入相关度的概念,构造辅助输出,使得匹配条件得以满足。在假设辅助输出可测时针对一类未知输入系统提出了一种降维观测器的设计方法。
事实上,很多控制过程中都有不同程度的延迟现象,因此对带有时滞性的系统观测器设计理论进行研究具有一定的应用和现实意义,文献[9]针对广义时滞系统的降维观测器进行了设计,并给出了在一定条件下降维观测器的具体形式。文献[10]针对一类Lipschitz非线性系统,基于Lyapunov稳定性理论研究了降维观测器设计的问题。文献[11]主要利用线性矩阵不等式(LMI)方法,研究一类离散时滞非线性系统的全维及降维观测器设计问题。针对降维观测器的应用,文献[12]利用正交原理,将故障状态与系统状态进行解耦,构造出了用于故障估计的降维观测器,为降低诊断算法的计算量,优化算法参数,设计了一种基于降维观测器的最优故障诊断算法。文献[13]设计了一种降维观测器来实现非线性动态系统中执行器故障的诊断,弥补了以往在研究实现执行器故障诊断时需要故障或故障导数以及干扰上界已知的不足。
广义系统可以用于描述更为普遍的实际系统,自提出后一直是研究热点[14-16]。目前,关于含非线性项时滞系统降维观测器的设计已经取得了一定的成果,但是针对广义系统降维观测器的研究较少,因此,研究含非线性项的时滞离散广义系统降维观测器的设计方法具有一定的积极意义。本文沿文献[11]的路线,将研究Lipschitz非线性时滞离散系统降维观测器的设计方法推广到广义系统的形式。利用线性矩阵不等式(LMI)方法,基于Lyapunov稳定性理论,设计一类Lipschitz非线性时滞离散广义系统的降维观测器,并保证降维观测器误差系统全局渐近稳定。
1 系统描述
考虑如下时滞广义系统:
(1)
其中,E∈Rn×n为异矩阵且满足rank(E)=q 假设1系统(1)的非线性部分Φ(x(k),x(k-d),u(k))满足Lipschitz条件: 其中,Lipschitz常数为LΦ。 根据假设2,系统(1)可以表示为: x(k+1)=TAx(k)+TAdx(k-d)+TΦ(x(k),x(k-d),u(k))+Ny(k+1), (2) 记: Φ′(x(k),x(k-d),u(k))=TΦ(x(k),x(k-d),u(k)), 则式(2)可以表示为: (3) 对状态变量x(k),x(k-d)进行如下形式的分块: x(k)=(x1(k)x2(k))T,x(k-d)=(x1(k-d)x2(k-d))T, 其中,x1(k),x1(k-d)∈Rp,x2(k),x2(k-d)∈Rn-p。 不失一般性,假设C=(Ip0),则有: y(k)=Cx(k)=x1(k),y(k-d)=Cx(k-d)=x1(k-d)。 (LIn-p)Ny(k+1)-Ly(k+1)。 (4) 本文分两种情况,依次设计系统的降维观测器。 ①系统不含Lipschitz非线性项的情况 当系统(1)中不含Lipschitz非线性项时,根据系统变换式(4)可设计如下降维观测器: (5) (6) ②系统含Lipschitz非线性项的情况 当系统(1)含有Lipschitz条件的非线性项时,根据系统变换式(4)可设计如下降维观测器: (LIn-p)Ny(k+1)-Ly(k+1), (7) (8) 其中: ΔΦk′=Φ′((y(k)x2(k))T,(y(k-d)x2(k-d))T,u(k))- 定理1若存在矩阵P,Q和L满足不等式(9),则式(5)为系统(1)不含非线性项的降维观测器: (9) 选取李雅普诺夫函数: 故有: 其中: 由Schur补引理可知,M1<0等价于不等式(9)误差系统渐进稳定,式(5)为系统(1)中不含非线性项的降维观测器。 定理2若存在矩阵P,Q和L满足不等式(10),则式(7)为系统(1)含非线性项的降维观测器: (10) 其中*为对称矩阵中对称部分。 记: ΔΦk′=Φ′((y(k)x2(k))T,(y(k-d)x2(k-d))T,u(k))- 选取李雅普诺夫函数: 由于Φ(x(k),x(k-d),u(k))满足Lipschitz条件,知: ΔΦk+1′TΔΦk+1′≤β2[e2T(k+1)e2(k+1)+e2T(k+1-d)e2(k+1-d)], 故有: 其中: 由Schur补引理知,M2<0 等价于不等式(10),ΔV<0 误差系统渐进稳定,式(7)为系统的降维观测器。 注:在判定降维观测器存在的充分条件时,定理1与定理2中分别构造了李雅普诺夫函数,其中定理2中李雅普诺夫函数的构造考虑到了系统的Lipschitz非线性部分,最后给出了降维观测器存在的充分条件。 例考虑系统(1)的参数如下: 系统中Lipschitz非线性项为: 由假设系统(1)可观测,可计算出行满滞矩阵[TN]中的矩阵T,N分别为: 则系统(1)通过变换可以得到式(2)形式, 与文献[11]中的数值算例相同,即: 利用线性矩阵不等式的求解方法,可求得降维观测器的增益矩阵: 可知降维观测器的误差系统渐近稳定,且降维观测器的误差收敛速度比文献[11]中全维观测器误差收敛速度更快。 针对一类非线性时滞离散广义系统,主要研究了降维观测器的设计问题。在系统状态观测器设计中,利用Lyapunov稳定性理论与Schur补引理得到了降维观测器存在的充分条件;在观测器的设计中,利用线性矩阵不等式(LMI)方法得到了观测器的增益矩阵。最后,通过算例验证了降维观测器设计方法的可行性。 目前,关于非线性系统降维观测器的设计,大多基于非线性项满足Lipschitz条件,而基于Lipschitz条件所得到的降维观测器具有一定的保守性,针对含不确定项的非线性时滞系统降维观测器的设计可作为进一步研究的方向。



2 降维观测器的设计



3 降维观测器存在的条件





4 算例

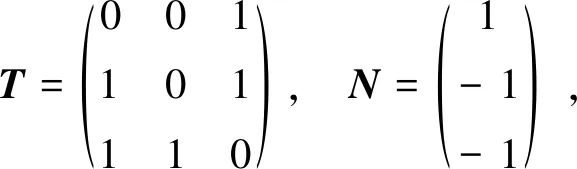
5 结语
