一种适用于高铁变形预测的组合模型建立方法

康昊华12，刘立龙*12

(1.桂林理工大学测绘地理信息学院， 广西桂林541004;2.广西空间信息与测绘重点实验室， 广西桂林541004)

高铁高铁沉降变形观测数据是反映高铁路线运营状况的重要指标。科学分析高铁沉降变形监测数据，建立实时变形预测模型，对高铁安全稳定运行具有重要意义。因此，在高铁路线投入运营后，仍然需要长期对其进行变形监测，并基于监测数据对后期变形趋势进行预测。

目前，常见变形预测模型的建立主要是基于一种数学手段，这些手段包括时间序列法、小波分析法、灰色理论和神经网络法等[1-4]。在实际工作中，单一的预测方法各有其优缺点，传统的灰色预测模型GM(1,1)作为最基本的预测模型，具有算法简单、预测结果可靠性高、较为方便等优点，而被广泛应用于高铁沉降预测评估工作中[5-6]；但在实际的运用过程中由于高铁工程的线上工程压力大，测量精度要求高，由其他因素带来的测量误差在其中被明显放大呈现出“小沉降，大波动”的现象[7]，因此在运用原始数据进行预测处理时往往不能获取较好预测结果；其次传统的GM(1,1)模型在预测较长时间的数据时，由于数据累加常常出现预测结果发散的现象，且在预测处理规律变化不明显、数据起伏较大的情况时结果并不理想。

针对上述单一法受原始数据受噪声影响大、长期预测不准确的问题，本文提出了一种基于小波去噪的自适应GM(1,1)-MC组合模型。首先运用小波去噪原理对原始监测数据进行去噪处理，消除原始数据中的随机扰动误差提升数据质量，随后运用自适应灰色预测模型进行预测淡化原始数据中老旧数据的影响，最后运用马尔科夫修正模型以期提高组合模型在趋势性分析上的预测精度和准确性。

1 基于小波的自适应GM(1,1)-MC组合模型原理

1.1 小波去噪原理

小波具有对多分辨率的时域与频域进行分析这一功能，通过对原始数据的多尺度分解与重构能够有效地剔除原始数据中的噪声扰动，从而提升变形数据的预测精度。通常情况下,本文将一个含噪声的信号表示为：

f(t)=s(t)+g(t)。

(1)

首先对含噪信号进行离散化的小波缩放，获得一组离散信号f(n)。

(2)

式中，ωf(j,k)是变换后的小波系数，j=1,2,3,…,J为分解尺度数，k为平移因子。随后针对性择取基函数对该信号进行一维小波，得到J尺度下的J个细节分量和J个近似分量。信号f(n)的正交小波变换的分解方法如式(3)：

(3)

其中，cj-1为近似小波系数，dj-1为细节小波系数。最后采用小波重构获取消噪之后的小波原信号估计值，其重构公式为：

(4)

1.2 自适应GM(1,1)模型

GM系列模型是灰色预测理论(grey system)中的最基本模型，尤其是GM(1,1)模型，其符号的具体含义：G(即Grey：灰色)，M(即Model：模型)，1(指1阶方程)，1(代表1个变量)。原始GM(1,1)预测模型的建立过程：

设x(0)为非负的等间隔离散序列：

x(0)=(x(0)(1),x(0)(2),…,x(0)(n))。

(5)

记x(0)的一次累加序列为：

x(1)=(x(1)(1),x(1)(2)…,x(1)(n)),

(6)

对累加序列进行求导获得原始GM(1,1)模型所使用的白化方程：

(7)

白化方程的解为：

(8)

在式(8)中可求出待定常数a、b的值，a为发展系数用以调控系统整体的发展局势；b为灰色作用量，其大小直接反映数据的波动变化情况。由式(7)可求出GM(1,1)模型的时间响应序列为：

(9)

通过数据累减获得GM(1,1)表达式为：

(10)

(11)

自适应GM(1,1)是对原始模型的改进[8-10]，将运用传统的GM(1,1)模型预测得到x(0)(n+1)添加到原始的预测序列当中，随后将原始数据中时间距离上离新预测值最远的的数据值x(0)(1)进行剔除，将新获得的预测值补充进入其中保持模型预测数据的等维；随后用替换过后的数据模组继续进行GM(1,1)模型建立与替换，如此循环直到完成对全部数据的处理。

1.3 马尔可夫模型

马尔科夫模型(markov model， MC)[10-12]认为自然界的随机事件的产生都具有一定的相关性，通过对前若干次随机事件的统计得出其概率分布，可以用来评估下一次随机事件的发展状态。具体操作为将观测值和预测值之间的误差进行状态划分，共划分为n个区间(一般取3～5个区间)，即相对误差从Sm通过k步转变到Sn的概率表示为：

(12)

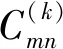
(13)

取离预测的观察时序最近的若干个已知状态数值，求取已知状态转移到预测状态所经历的具体步长，然后再从状态转移矩阵中找到相对应的转移概率，将处于每个状态Si(i=1,2,3,…)进行概率统计，找出处于哪个Si(i=1,2,3,…)中的概率和最大，这个预测值就处于相应的状态区间中，由此可得修正值为：

(14)

1.4 基于小波的自适应GM(1,1)-MC组合模型

现依据高铁变形监测工作的实际情况结合各模型的特点建立一种基于小波的自适应GM(1,1)-MC组合模型，具体流程如下。

Step1：小波数据处理。选择合适的小波基函数对实际采集到的变形数据进行去噪处理，并通过对小波分解层数与小波阈值选取进行研究，获取最佳的小波去噪方式。

Step2：对分解到低频序列的变形数据采用自适应灰色模型进行预测，获取小波灰色模型的预测结果。

Step3：引入马尔可夫修正模型对小波灰色模型的预测结果进行修正。模型预测流程如图1所示。

2 工程算例

2.1 算例1

本文选用贵广高铁某路段路基基底沉降板中LO1点连续20期(观测时间为2014年4月至2014年10月，观测间隔为7 d)的垂直方向位移观测量为原始计算数据。采用原始测量数据的前15期作为基础拟合样本，后5期数据为检验样本。

为综合比较各模型的预测效果，本文设计了3种方案进行对比实验：自适应GM(1,1)模型(方案1)；对原始数据选用sym4小波进行3尺度的小波分解与逆向重构去噪后再建立自适应GM(1,1)模型(方案2)；在方案2的基础上引入马尔科夫链进行修正，残差值状态划分如下s1=[-5.77 %,-1.63 %]，s2=[-1.62 %,2.65 %]，s3=[2.66 %,4.17 %](方案3)。各模型的预测结果如表1所示；实测值与3种方案的预测值对比曲线如图2所示；3种方案的残差比较结果如图3所示。

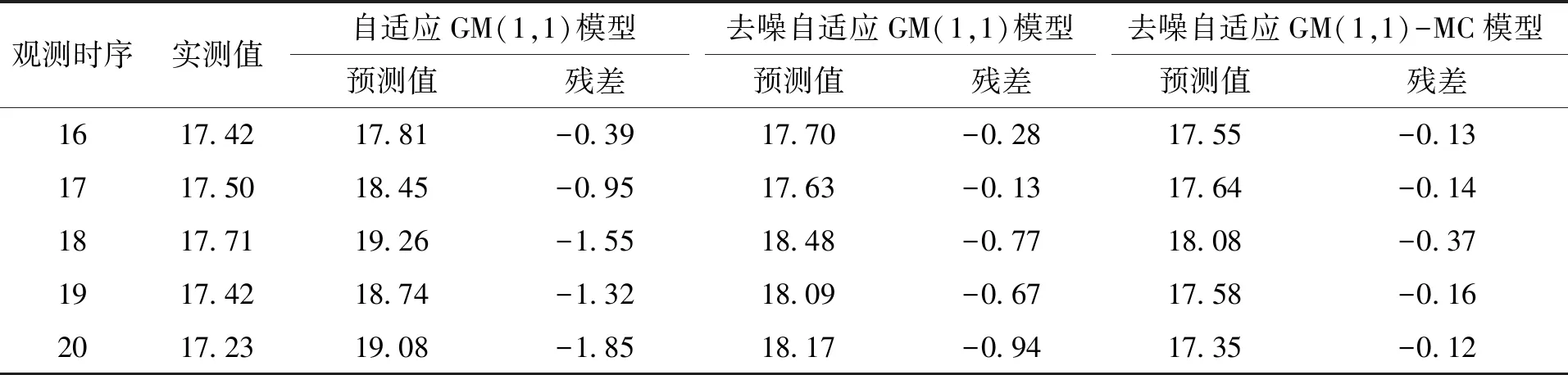
表1 各模型预测结果对比Tab.1 Comparison of predicted results of each model mm

如图2所示，当沉降监测点的沉降曲线总体呈现平稳变化趋势时，方案1随着预测期数的增多与实测值之间的偏离程度愈发明显，方案2与方案3呈现出一定的收敛趋势，且方案3与实测值的贴合程度最好。由图3可见方案2、3的残差在初期较为平稳，随着预测时间的增加后方案2的发散速度明显快于方案3，而方案1的残差相对而言一直处于较大状态。从表1中可以看出，方案1的预测稳定性不强，残差最大绝对值为1.85 mm远高于方案2与方案3。方案3的预测结果最好，残差最小绝对值为0.12 mm,最大绝对值仅为0.37 mm。

图2 实测值与3种方案的预测值对比
Fig.2 Comparison of measured values andpredicted values of three schemes

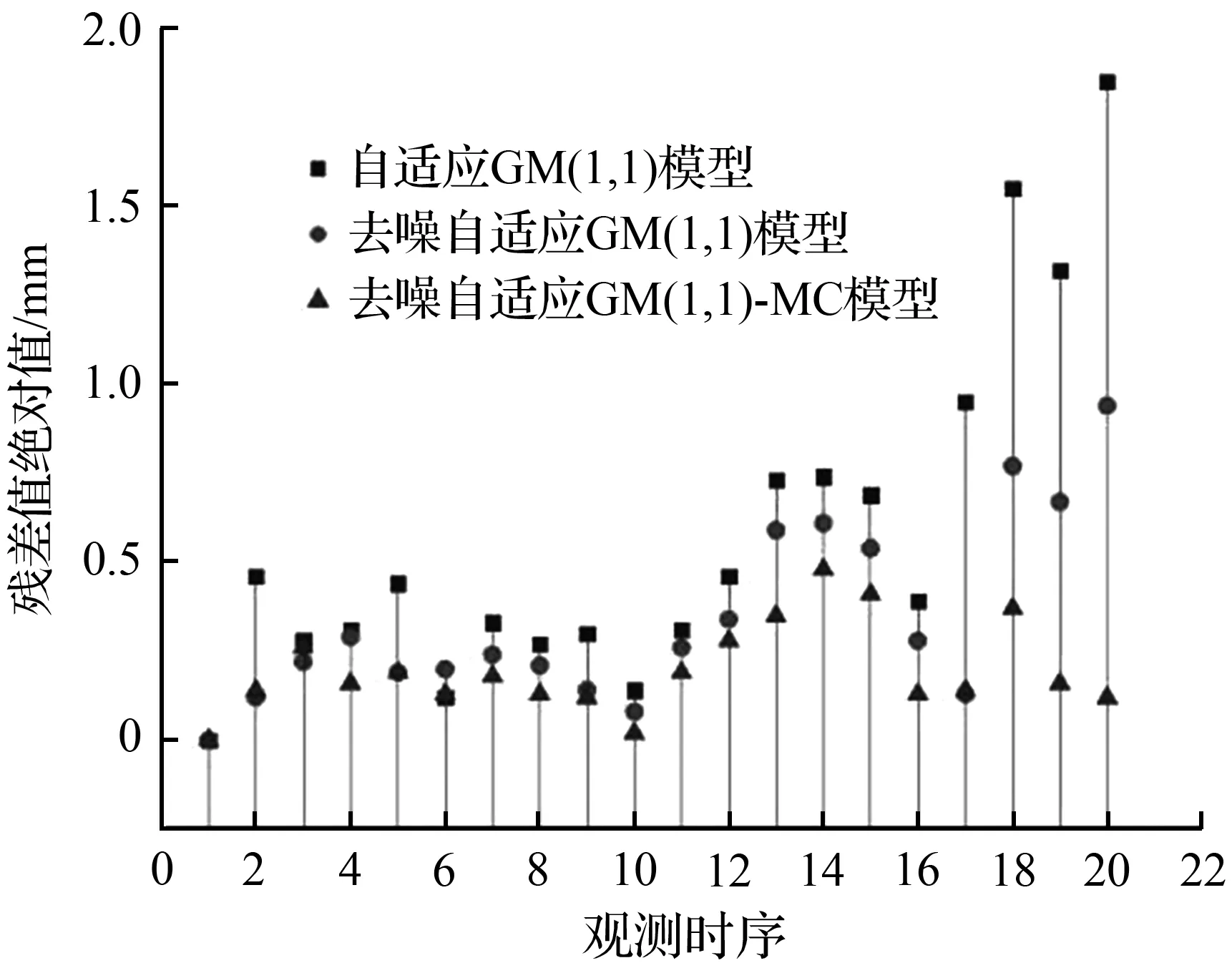
图3 残差图
Fig.3 Residual graph

2.2 算例2

鉴于实际高铁工程中常见的工程体突变情况，即前期观测数据较为稳定，中期某一时段出现大幅变形，随后又趋于稳定，本文另选用了某高速铁路某路基沉降监测数据25期(观测时间为2015年6月至2016年3月，观测间隔为7 d)，前20期作为基础拟合样本，后5期数据为检验样本。

建立与算例1相同的3种方案进行对比分析，各模型的预测结果如表2所示，图4为实测值与3种方案的预测值对比曲线。3种方案的残差比较结果如图5所示。

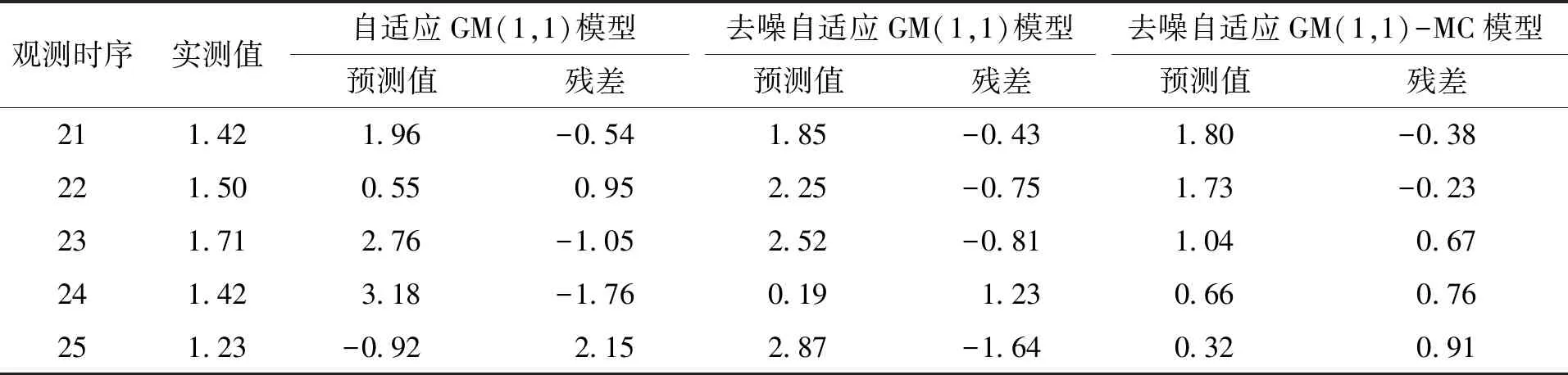
表2 突变型工程体预测结果比较Tab.2 Comparison of prediction results for catastrophic engineering bodies mm

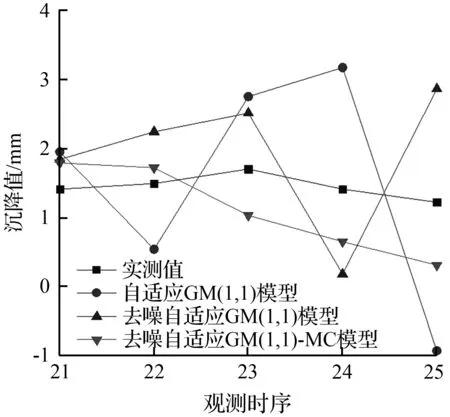
图4 突变型工程体预测值对比
Fig.4 Comparison of prediction values forcatastrophic engineering bodies

图5 突变型工程体残差图
Fig.5 Residual diagram of catastrophicengineering body

从表2可知，方案1的预测结果较差，残差最大绝对值为2.15 mm，最小绝对值为0.54 mm，与实测值出现明显偏差。方案2与方案3的拟合效果明显优于方案1，且方案3预测结果更好残差最小绝对值为0.23 mm,最大绝对值仅为0.91 mm。可见在经过小波去噪处理后的自适应GM(1,1)模型在预测突变体工程上能够取得较好的效果，再经过马尔科夫模型对残差数据进行修正后能够获取得更为准确的预测结果。

由图4可知，在变形监测点变化情况较为剧烈时,方案1的预测曲线明显偏离实测值，在中部波动较大位置与实测曲线偏差较大。与实测曲线吻合度最高的是方案3，贴合程度最好且无明显突变发生，有效反应了实测曲线的细节信息。从图5中看出方案1的残差值的明显大于另外两种方案，经过小波去噪后处理的方案2与方案3残差值存在一个明显的收敛趋势。

为进一步综合评价本文方法，选用了均方根误差与平均绝对误差两项评价指标结果见表3。

表3 3种方案的预测精度比较Tab.3 Comparisons of prediction accuracy of three schemes mm

由表3可知，方案1的预测精度较低，两个算例的均方根误差分别为1.31 mm与1.42mm，方案2的预测精度较好于方案1。而本文方法的预测精度明显较高，均方根误差分别为0.21 mm与0.64 mm，与方案1相比改善率达到了83.96 %与54.93 %，平均绝对误差分别仅为0.18 mm与0.59 mm。可见本文方法在高铁预测的平稳型与突变型情况中均能取得较好的预测结果。

综上，本文方法首先利用小波分析作为数据分析的预处理工具，能有效消除原始数据中的噪声部分；然后采用自适应灰色预测模型对数据进行拟合，找出其变化趋势；最后，通过马尔可夫模型进行修正可以有效削弱观测时间变长而产生的预测残差迅速扩大的情况，提升模型的整体预测精度。

3 结语

针对高铁变形预测中呈现出的原始数据受噪声影响大与长期预测不准确的问题，本文将基于小波去噪的自适应GM(1,1)-MC组合模型用于高铁沉降变形监测中，实验结果表明：

①本文方法针对各单一模型的不足进行了一定程度的补充具有更好的实际表现效果。在实际工作中采用基于小波的自适应GM(1,1)-MC预测法来进行高铁沉降变形预测中具有一定的可行性。

②利用小波对原始的高铁沉降数据进行处理可以有效的将测量过程中的各种因素引起的噪声进行消除，提升了原始数据的质量为后续的预测处理打下了良好的基础。自适应GM(1,1)-MC组合模型能够较好地发挥新息的价值通过对模型原始数据进行深度挖掘增强预测数据对变化趋势的敏感性，消除长期预测造成的数据发散现象，获得更高精度的预测值。

③本文选取的去噪小波与分解层数对模型的预测精度有较大影响，但在实验过程中仅是基于经验处理与小样本对比得出，更为合理的参数确定方法有待进一步研究。