基于粒子群算法的汽车TBW综合换档规律研究
2019-08-28吕娜娜郭林2曲金玉郭政斌米家杉赵卓文
吕娜娜 ,郭林2 ,曲金玉* ,郭政斌 ,米家杉 ,赵卓文
(1.山东理工大学交通与车辆工程学院, 山东淄博255049;2.雷沃重工股份有限公司诸城车辆厂,山东潍坊262200)
0 引言
换挡规律的优劣对汽车的动力性、燃油经济性和安全性等都有较大的影响[1],其制定和优化是国内外的很多学者们的研究热点。但是对汽车换挡规律的研究多集中在对提高经济性能或动力性能单个方面的研究,较少同时考虑兼顾到车辆的动力性和经济性以制定对应的换挡规律进行优化研究,缺乏实际的应用价值。如文献[2]中,基于动态规划算法,以油耗最小为优化目标,制定换档规律并优化,使车辆燃油经济性有了明显提高,但未同时考虑汽车的动力性要求;文献[3]中,基于实际运行工况,利用Cruise仿真软件得到优化后的AMT换挡规律,结果具有明显的油耗优势;文献[4]中,对所制定的换档规律,以加速时间为优化目标,优化得到的换档规律动力性能提高。
本文以汽车六档线控自动变速器(transmission-by-wire,TBW)作为研究对象,TBW是采用线控方式驱动,具有结构紧凑、可动力性换档、无机械或液压换档部件、运行能耗低等优点[5]。在制定双参数经济性和动力性换挡规律的基础上,提出一种综合性换档规律的制定与优化方法,解决了同时兼顾汽车动力性和经济性的要求的问题。该方法通过制定加速度平均变化率和整车油耗变化率的分目标优化函数,取权重求和得到总目标优化函数,以不同加速油门开度下的各档位的换档点车速作为主要优化变量,运用多目标粒子群算法进行迭代寻优求解得到综合性换挡规律曲线,并分别从经济性能和动力性能指标对优化前后的换挡规律进行对比分析,结果表明,优化后的综合性换挡规律,相比优化前的动力性换挡规律和经济性换挡规律,对应其经济性能和动力性能在各档位有不同程度提升,提高了整车性能。
1 整车参数
本文针对汽车六档线控自动变速器综合换挡规律的制定与优化进行研究,主要整车参数见表1。

表1 主要整车参数Tab.1 Main vehicle parameters
2 发动机的工作特性
本文根据发动机稳态转矩特性台架实验和发动机油耗特性试验,可得其转矩特性曲面图和燃油消耗量特性图,分别如图1、图2所示。
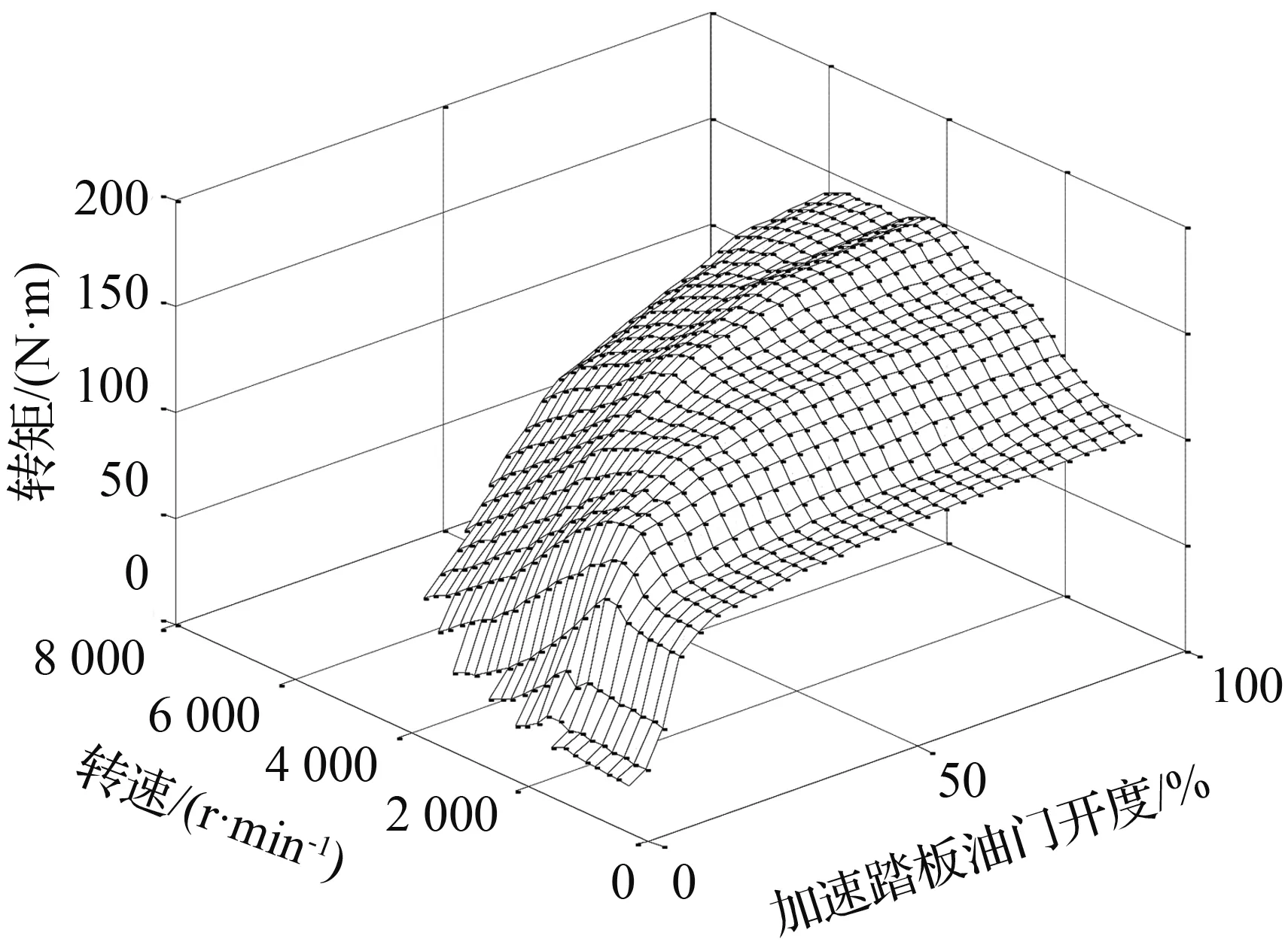
图1 转矩特性图
Fig.1 Diagram of torque characteristic
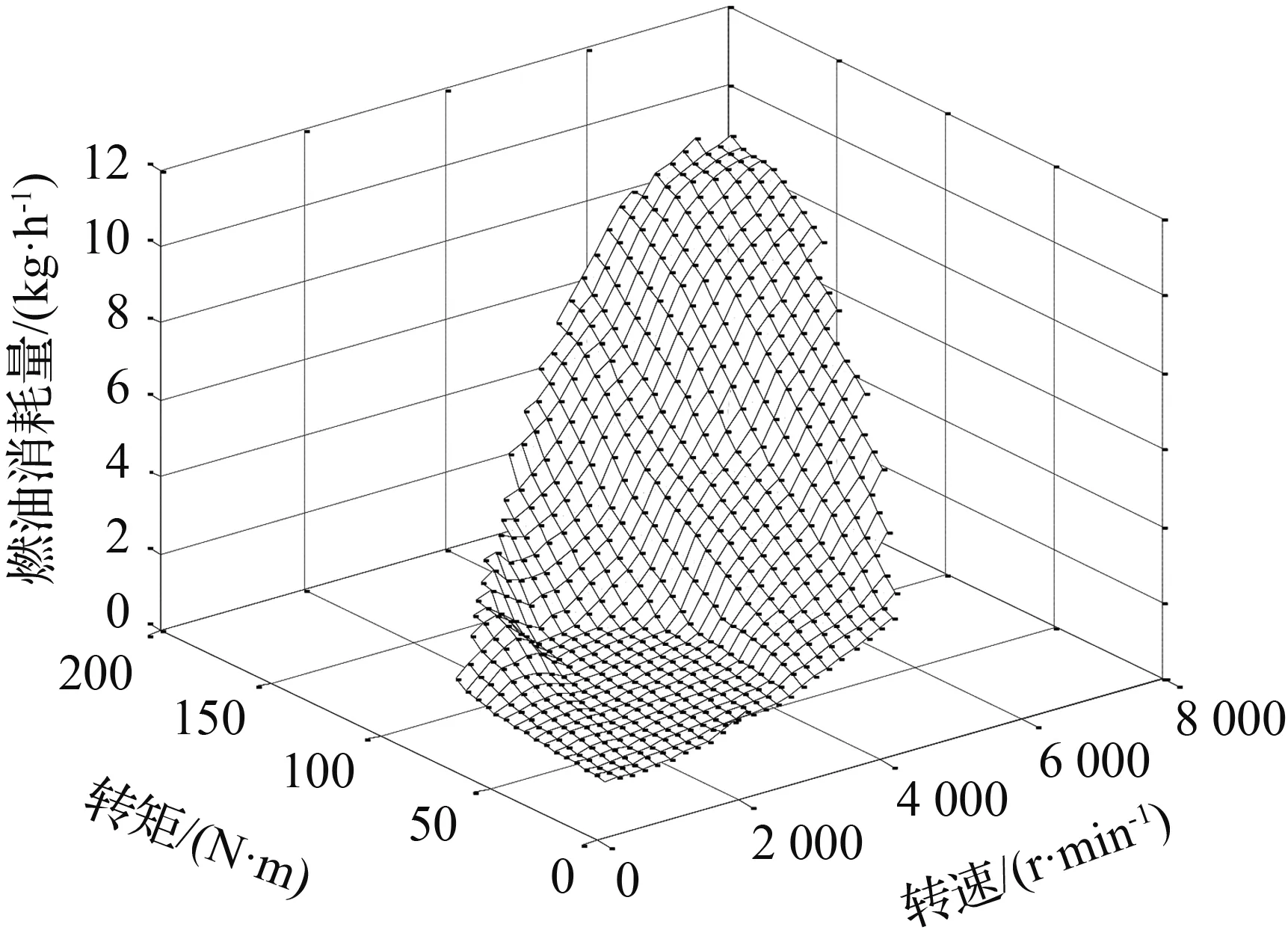
图2 燃油消耗量特性图
Fig.2 Chart of fuel consumption characteristics
3 双参数换档规律的制定
3.1 经济性换档规律的制定
经济性换档规律是指在保证汽车满足经济性要求的换档点进行换档,并使油耗量尽可能达到最小的换档规律[6]。在本文中,为了获得最佳换档点,选择采用最低燃油消耗率即比油耗作为制定依据,在比油耗—车速关系曲线中,取同一油门开度下的相邻两档位间交叉点的车速作为对应档位的换档点车速,即令:
ge(n)=ge(n+1)。
(1)
依次可得各个档位的最佳的升档换档点,然后在该制定的升档点的基础上,进行等速差延迟即可得到各个档位的降档换档点车速,再通过MATLAB进行多项式拟合插值得最佳经济性换档规律。
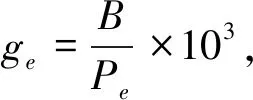
ge=ge(ne,Te)。
(2)
由于发动机比油耗与其转速与转矩的对应关系相对复杂,为增加精确度,可对其进行曲线拟合插值成二元五次函数曲线,表达式为:
(3)
式中,g0,g01,g10,…,g05,g50为常系数。
由发动机的转矩特性可知,在同一油门开度α下,发动机转矩与转速的关系可表示为Te=Te(ne,α),即在同一油门开度下,发动机转矩与转速的关系可以拟合成四次函数Te=Te(ne),得:
(4)
式中,t1,t2,t3,t4,t5为常系数。
则可得发动机比油耗与转速和油门开度之间的关系,即ge=ge(ne,α),将转速公式代入,可得发动机比油耗与车速和油门开度之间的关系为:
(5)
综上分析可得,升档换档点方程式为:
(6)
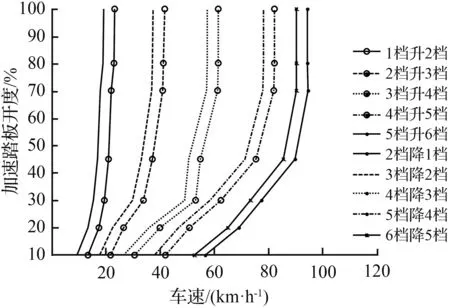
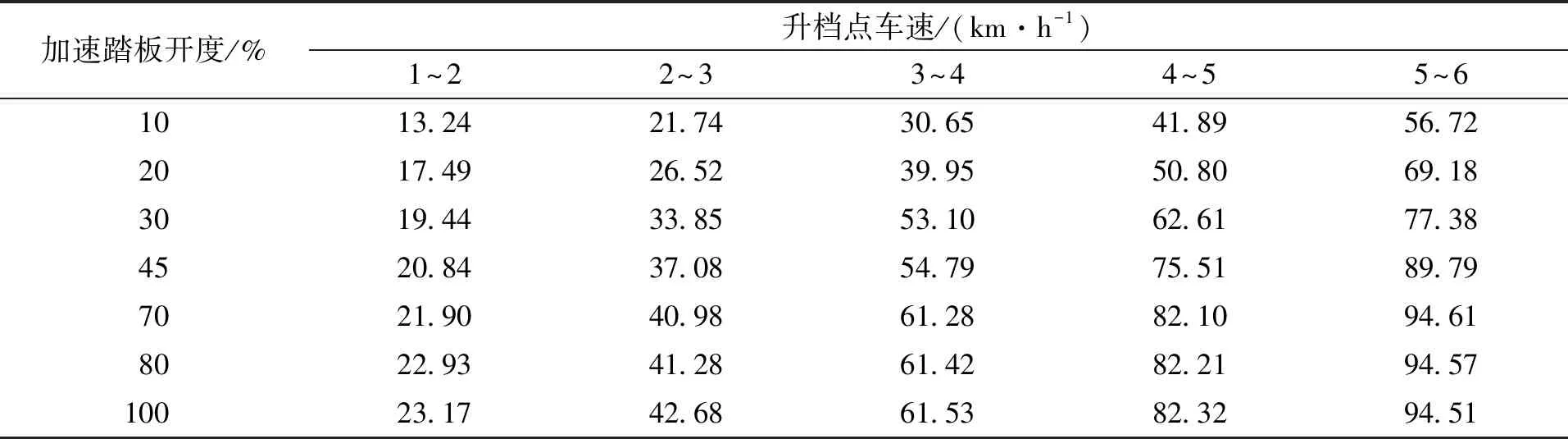
在MATLAB中编程求取,可得在不同的油门开度下,各个档位的比油耗与车速之间的曲线关系图,进而可得相邻两档位的比油耗的相交点车速即为各个档位的换档点。下面以100 %油门开度下求取各档位升档换档点车速为例,进行详细说明。通过对该油门开度下发动机转矩与转速以及发动机比油耗与转速和转矩进行曲线拟合分别得出他们的函数关系曲线图,对升档换档点方程式进行编程求解,可得出在100 %油门开度下各档位的升档点,将各个档位关于比油耗—车速的曲线进行适当简化局部放大处理,得到该油门开度下各档位的升档点如图3所示。图中,相邻两档的交点处车速即为对应档位的升档点车速。同求取100 %油门开度下的各档位升档点车速做法,在本文中,分别取油门开度为10 %,20 %,30 %,45 %,70 %,80 %,100 %为例,可求取出各档位的升档点车速。所求的各档位的升档换档点车速汇总于表2中。
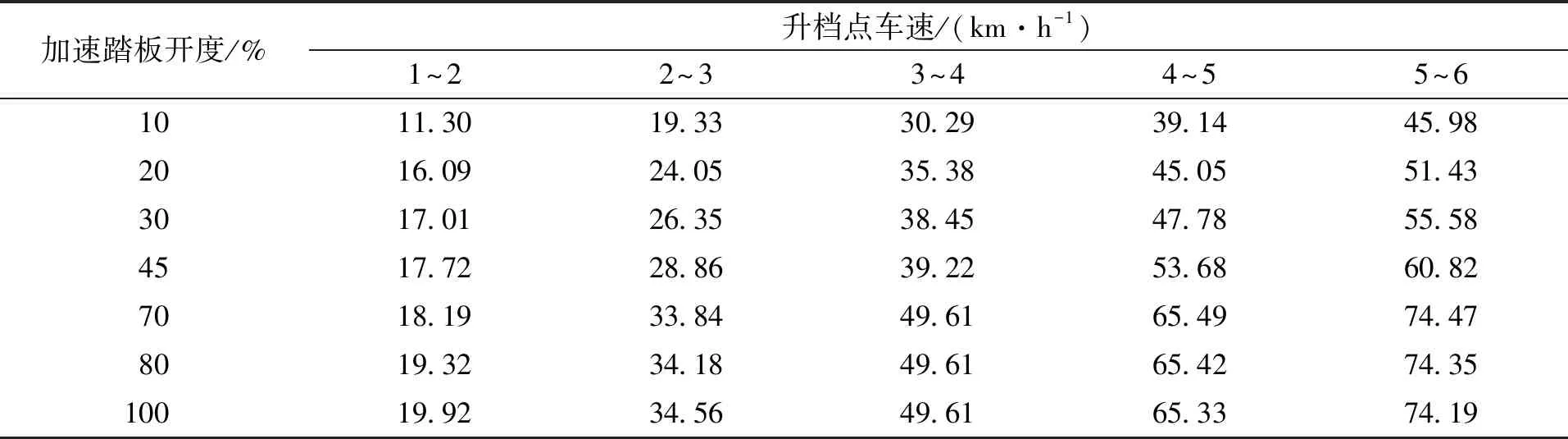
表2 经济性升档换档表Tab.2 Economic shift table for upgrade
在制定经济性降档点车速时,为保证经济性要求,减少耗油量,经济性换档点的车速相对要小,称为提前型换档[8-9]。因此为避免循环换档问题的发生,在制定好升档换档点的基础上采用4.1 km/h的等速差换档延迟,作为降档时的车速点。最后,将各个档位在不同油门开度下的升档和降档点车速分别进行Polynomial多项式拟合插值,得该最佳经济性换档规律曲线,如图4所示。

图3 全油门开度下的升档点
Fig.3 Upgrade point under full throttle opening
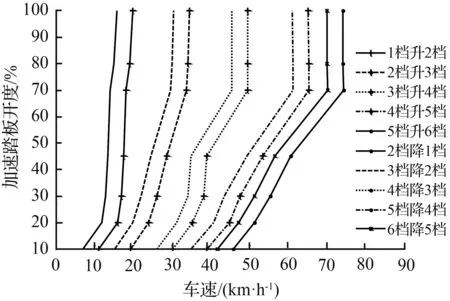
图4 经济性换档规律曲线
Fig.4 Curve of economic shifting schedule
3.2 动力性换档规律的制定
动力性换档规律曲线的制定原则是保证汽车在获得良好的动力性要求的情况下进行换档,能够最大限度的发挥发动机的功率和车辆的牵引特性[10]。在本文中,其换档点的确定是以汽车获得最大加速度为制定依据,在同一油门开度下,以相邻两档间的车速—加速度的曲线的交点的车速作为相应档位的换档点,即:
(7)
依次可得各个档位的最佳的升档换档点车速,在升档点制定的基础上,再进行等速延迟即可制定出各个档位的降档换档点车速,然后通过MATLAB进行Polynomial多项式拟合插值即可绘制得最佳动力性换档规律曲线。
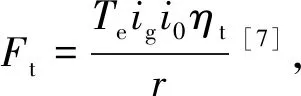
(8)

由于本课题研究的是汽车在正常道路上行驶,故其坡度角不大,即cosα≈1,sinα≈tanα,所以式(8)可简化为:
(9)
式(9)可以表示成加速度的方程式,为:
(10)
根据发动机转矩特性曲线可得出发动机转矩与转速和油门开度的关系,即Te=f(n,α)。为提高结果的精确性,可将在同一油门开度下,发动机转矩与转速的关系,拟合成四次函数,其函数关系为:
Te=t1n4+t2n3+t3n2+t4n+t5,
(11)
式中,t1,t2,t3,t4,t5为常系数。
进而,可得在同一油门开度下,发动机转矩与汽车行驶速度之间的关系为:
(12)
综合以上分析,可得换档点方程式为:
(13)
在MATLAB中编程求取,可得在不同的油门开度下,各个档位的加速度与车速之间的曲线关系图,进而可得相邻两档位的加速度的相交点车速即为各个档位的换档点。下面以100 %油门开度下求取各档位升档换档点车速为例,进行详细说明。通过对该油门开度下发动机转矩与转速进行曲线拟合得出他们的函数关系曲线图,对升档换档点方程式进行编程求解,可得在100 %油门开度下各档位的升档点,并将各个档位关于加速度—车速的曲线进行适当简化局部放大处理,得到该油门开度下各档位的升档点如图5所示。图中,相邻两档的交点处车速即为对应档位的升档点车速。同求取100 %油门开度下的各档位升档点车速做法,在本文中,分别取油门开度为10 %,20 %,30 %,45 %,70 %,80 %,100 %为例,可求取出各档位的升档点车速。所求的各档位的升档换档点车速汇总于表3中。
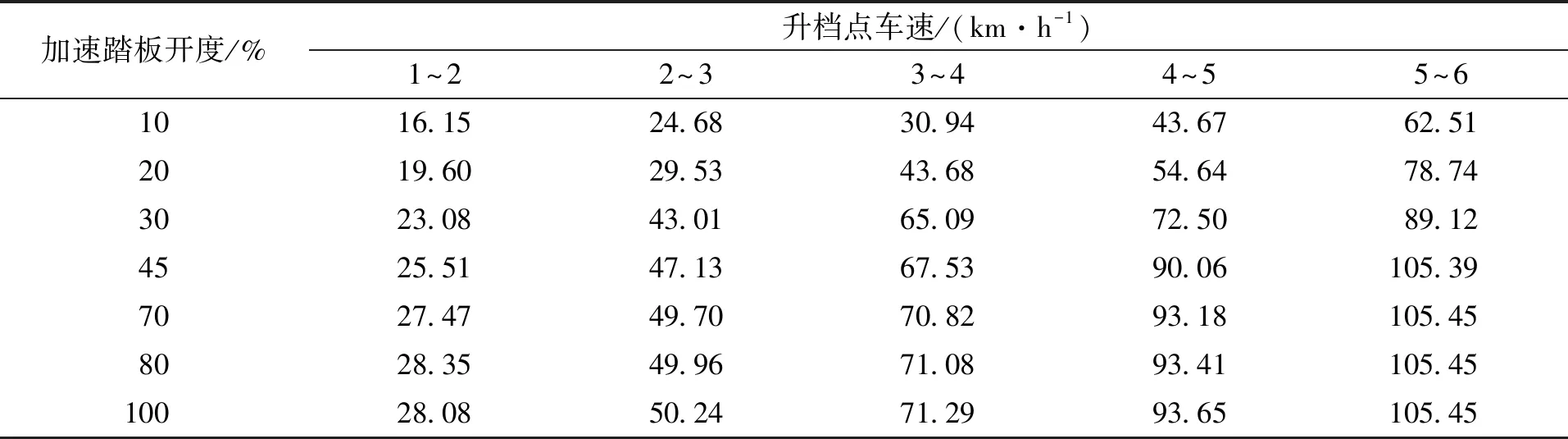
表3 动力性升档换档表Tab.3 Dynamic shift table for upgrade
在制定动力性降档点车速时,为保证动力性要求,得到较大输出扭矩,动力性换档的车速相对要大,又称为延迟型换档[11]。因此为避免循环换档问题的发生,在制定好升档点的基础上采用4.3 km/h的换档延迟,作为降档时的车速点。最后,将各个档位在不同油门开度下的换档点车速进行Polynomial多项式拟合插值可得该动力性换档规律曲线,如图6所示。
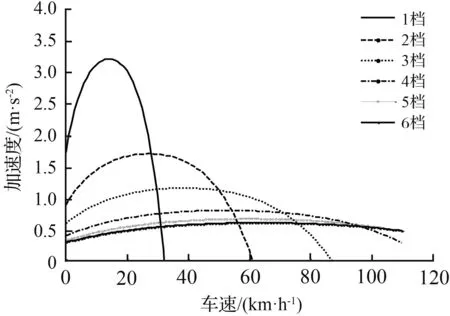
图5 全油门开度下的升档点
Fig.5 Upgrade point under full throttle opening
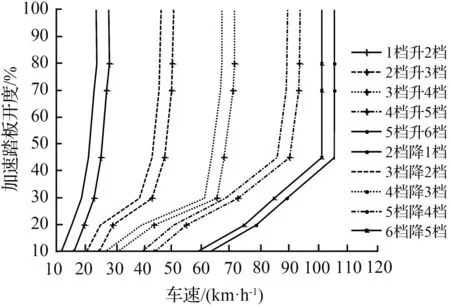
图6 动力性换档规律曲线
Fig.6 Curve of dynamic shifting schedule
4 基于粒子群算法制定综合性换档规律
粒子群算法(particle swarm optimization, PSO)。它从随机解出发,利用群体中的个体对信息的共享,追随当前搜索到的最优解来寻找全局最优,并通过适应度来评价解的品质[12]。具有实现容易、精度高、收敛快等优点。
4.1 建立优化目标函数
对各档位的加速度变化率取均值,得其平均变化率,作为评价整车动力性的指标。采用归一化去量纲方法,得动力性优化目标函数Δ1。
(14)
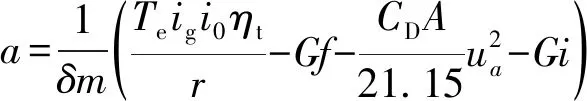
以输出的实际功率对时间的积分可作为整车能耗的计算。那么本文提出将整车能耗相对于最大能耗值和最小能耗值的平均变化率作为评价整车经济性的指标,采用归一化去量纲法,得经济性优化目标函数Δ2。
(15)
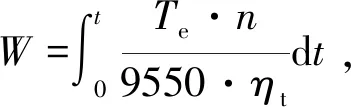
为兼顾整车动力性和经济性要求,权衡加速度和整车能耗的变化,引入权重系数d1,d2,并将其进行归一化处理,得总优化目标函数Δ。
Δ=d1×Δ1+d2×Δ2,
(16)
式中,d1,d2分别对应动力性和经济性指标权重系数,且d1+d2=1。
4.2 优化变量
结合本文TBW系统各相关常量参数均确定的特点可知,影响汽车动力性和经济性的变量参数为在不同油门开度下各档位换档点的车速,又因上述所建立的总优化函数数学模型可知,其中的权重系数d1,d2将会在一定的范围内进行变化波动,且两者相加为1,则优化其中之一即可。因此,确定本文的优化变量为
xi=[vi1,vi2,vi3,vi4,vi5,vi6,vi7,d1], (i=1,2,3,4,5),
(17)
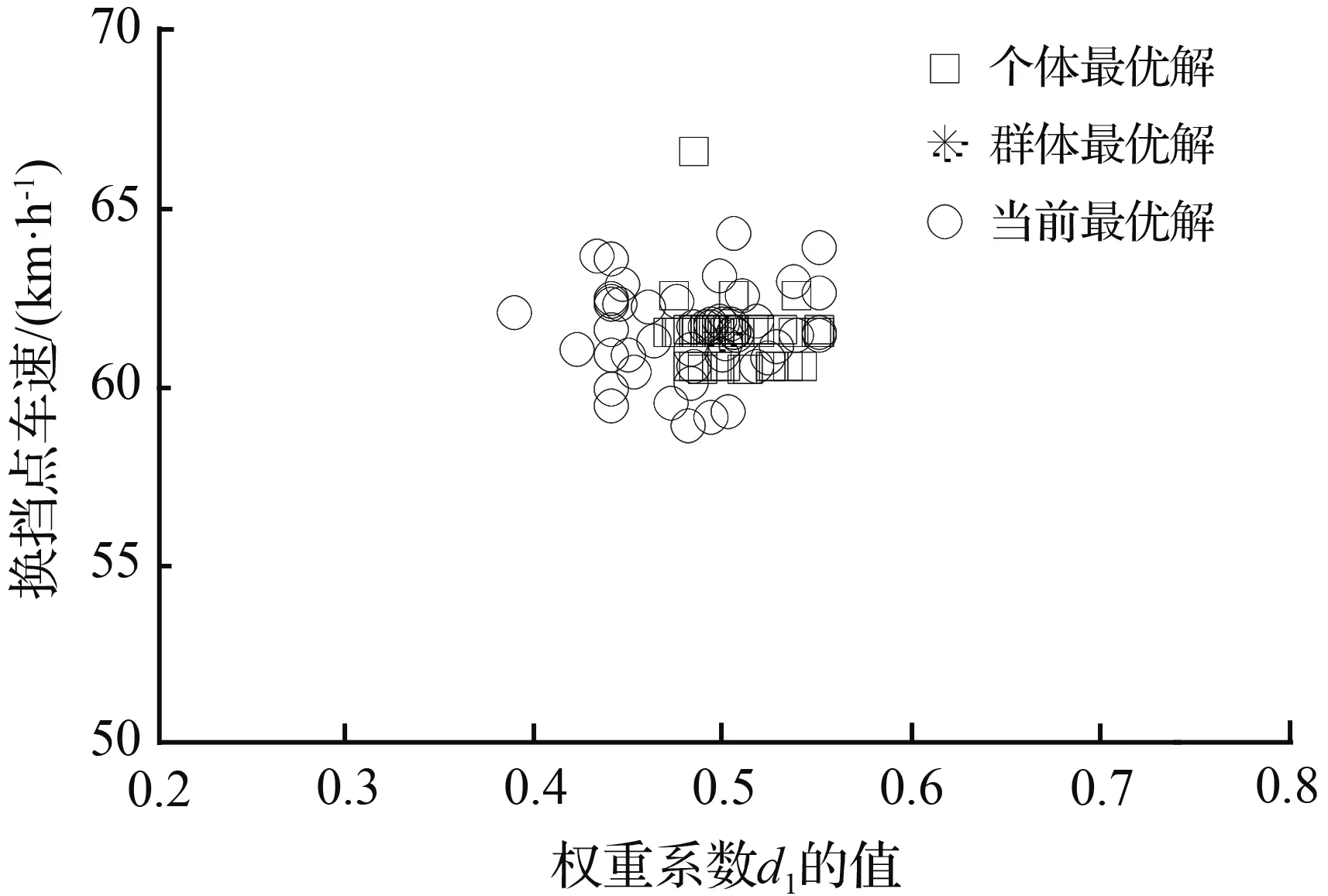
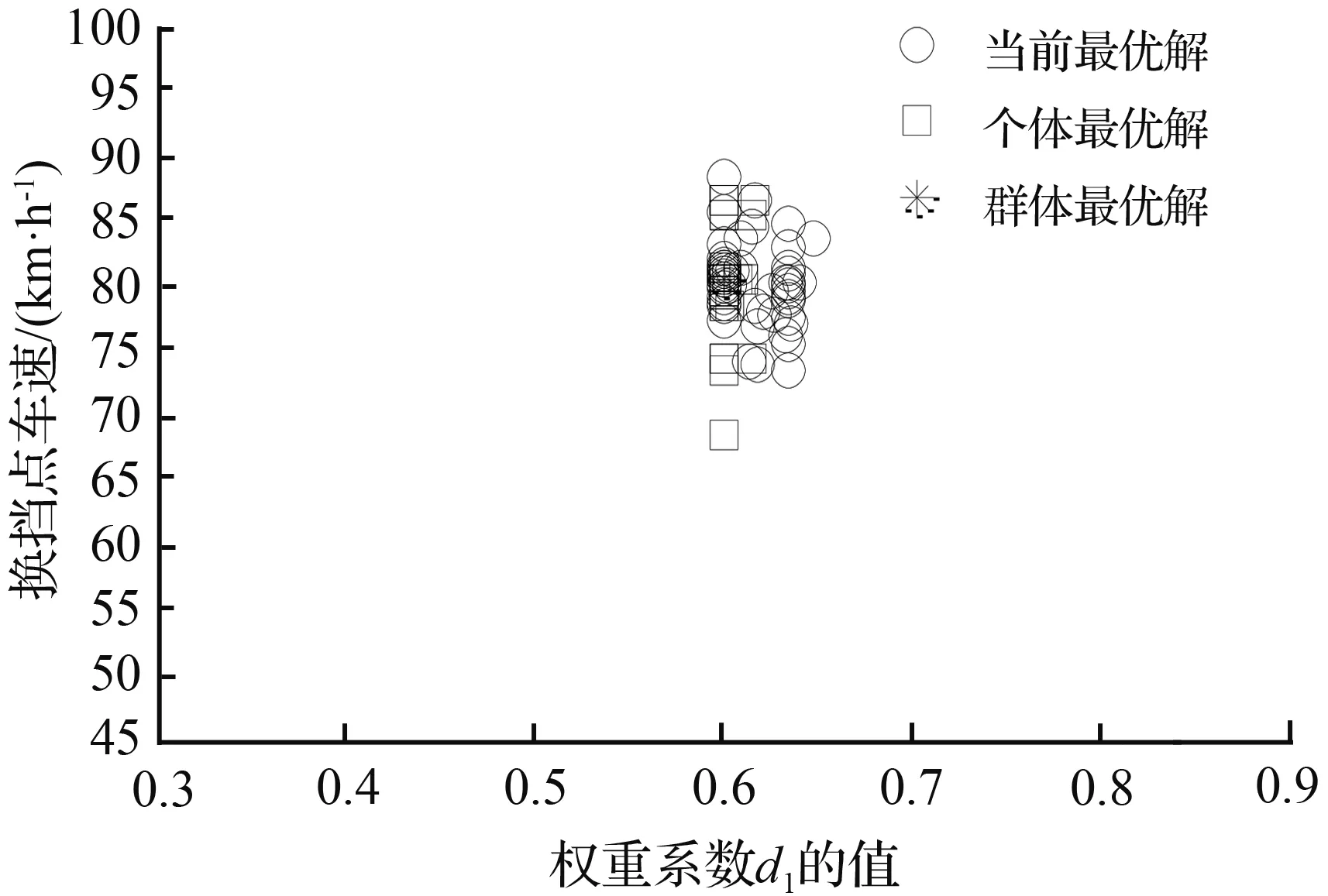
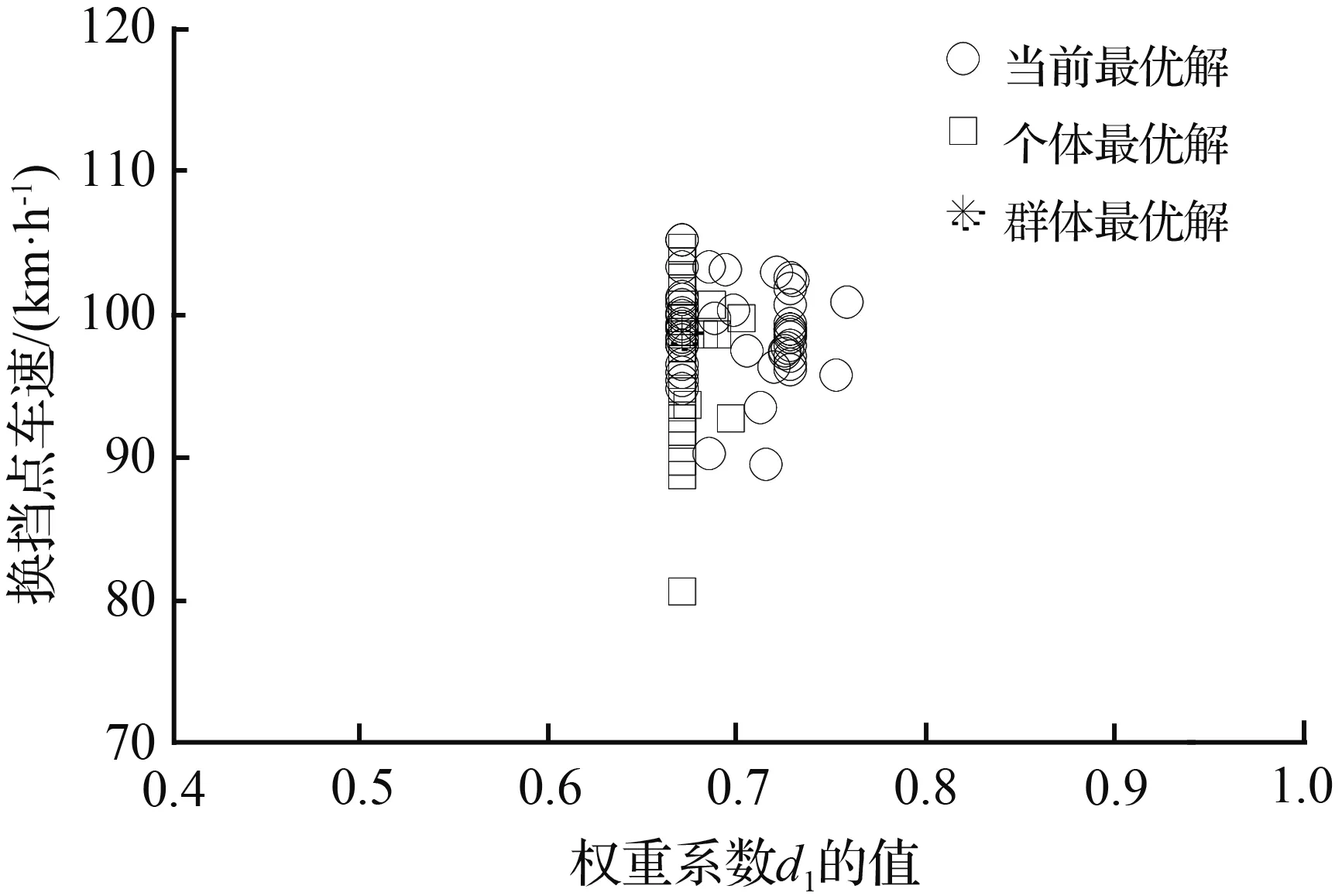
式中,i表示为各个档位;xi表示车辆处于i档时的优化变量;vi1,vi2,vi3,vi4,vi5,vi6,vi7分别表示汽车在i档时的10 %,20 %,30 %,45 %,70 %,80 %,100 %的油门开度下的升档点车速;d1为动力性指标权重系数(0 档位的变化受控制器控制,各档位的速度也要考虑当前档位,最高档不能升档,最低档无法降档,中间区域可以升档、降档或不变。汽车的行驶速度一般在最小车速和最大车速的80 %之间[13],而在不同档位下,汽车行驶速度介于当前档位的最大速度与最小速度之间,即所优化变量的约束条件为 (18) 其中,vi·min和vi·max的确定原则为,根据汽车动力性换档规律和经济性换档规律的延迟性和提前性的特点,则综合性换档点车速会介于经济性换档点车速和动力性换档点车速之间。为缩短变量优化范围,提高优化效率,将不同油门开度下的不同档位的经济性换档点车速定为当前档位的最小速度vi·min,将不同油门开度下的不同档位的动力性换档点车速定为当前档位的最大速度vi·max。 本文采用多目标粒子群算法对总目标函数和优化变量进行迭代寻优求解,其优化步骤如图7所示。在此次优化过程中,根据总目标优化函数的复杂程度,设置粒子数为20,学习因子c1和c2均为2,惯性权重为0.86,进化次数为100,粒子飞行的最大速度取参数变化范围的19 %。在本次的优化过程中,需要对不同油门开度下的总目标函数分别进行迭代寻优求解。下面以全油门开度下的各档位综合升档规律曲线优化求解为例进行详细说明。分别确定在该油门开度下各档位的总目标函数方程式,以各档位下的换挡点车速和动力性指标权重系数作为待优化变量,根据上述双参数经济性和动力性换挡规律曲线以及权重系数的取值范围确定各个待优化变量的约束条件,通过在MATLAB的PSO工具箱中调用该数学模型,并进行编程求解,使优化变量和函数值在迭代次数区间中不断的迭代寻优求解,最后得其各档位的适应度值收敛情况以及各档位的粒子寻优动态图解,其中1-2档的优化结果迭代过程的适应度值随迭代次数的变化曲线如图8所示,1~5档的粒子寻优图解如图9所示。 图7 粒子群算法优化步骤 图8 适应度值的收敛曲线 (a) 1档升2档的寻优图解 (b) 2档升3档的寻优图解 (c) 3档升4档的寻优图解 (d) 4档升5档的寻优图解 (e) 5档升6档的寻优图解 图10 综合性换档规律曲线Fig.10 Curve of comprehensive shifting schedule 由图8可知,粒子种群在第80代左右已实现平稳收敛,优化效果良好,由图9可知,优化变量换挡点车速的优化结果:1~5档的换档点车速分别为23.17、42.68、61.53、82.32、94.51 km/h。同理,可迭代求解出各个油门开度下的各档位升档换档点车速值。本文分别取油门开度为10 %,20 %,30 %,45 %,70 %,80 %,100 %,优化得到的换档点车速列于表4中。为避免循环换档问题的发生,采用4.2km/h的等速差延迟,即可得其降档点车速,最后通过曲线拟合插值可得其综合性换档规律曲线如图10所示。 表4 综合性升档换挡表Tab.4 Comprehensive shift table for upgrade 将上述优化结果带入建立的换挡依据数学模型中,以加速度和比油耗分别作为评价汽车动力性和经济性的性能指标,加速度越大,动力性越好,比油耗越低,经济性越好。计算得到各个挡位在不同的油门开度下优化前的经济性换挡规律和优化后的综合性换挡规律的加速度值如图11所示,优化前的动力性换挡规律和优化后的综合性换挡规律的比油耗值如图12所示。 图11 优化前后动力性能指标值 图12 优化前后经济性能指标值 结合前文对优化前经济性换挡规律和动力性换挡规律的制定,分析该优化结果,优化后的综合换挡规律,综合性能指标达到预期要求。其中,汽车的加速度值低于优化前的动力性换挡规律,但是,较优化前的经济性换挡规律在各个档位都有不同程度的提高,各挡位的改善率分别为10.64 %、12.53 %、14.48 %、13.76 %、14.79 %,可见,各挡优化效果相对均衡,平均改善率可达到13.24 %;汽车的比油耗值高于优化前的经济性换挡规律,但是,较优化前的动力性换挡规律有明显的降低,各挡位改善率平均可达到3.72 %,当汽车在高档位运行时,比油耗曲线会出现小幅度增长趋势,说明在高档位大油门开度下,经济性优化效果不明显。 针对汽车六档TBW,分别制定满足经济性和动力性要求的双参数经济性和动力性换档规律曲线,然后搭建基于粒子群算法的综合性换档规律模型,将整车能耗变化率和加速度平均变化率进行权重求和,建立总目标优化函数,以各换档点车速和权重系数为控制变量的优化问题。通过选择合适的优化参数,求解各油门开度下的各档位的适应度值收敛曲线以及粒子寻优图解,得出优化结果并制定综合性换挡规律,并将优化结果带入建立的动力性能和经济性能指标的数学模型中进行分析对比。优化后的综合性换档规律,较优化前的经济性换挡规律,动力性能平均改善率达到13.24 %,较优化前的动力性换挡规律,经济性能平均改善率达到3.72 %。本文通过运用多目标粒子群算法优化求解,确定出整车能耗与加速度之间的定量关系,制定的综合性换挡规律可兼顾汽车动力性和经济性的需求,此研究方法与结果对实际的设计研究具有一定的借鉴意义,并为后期的整车试验奠定了理论基础。4.3 变量约束
4.4 粒子群算法应用
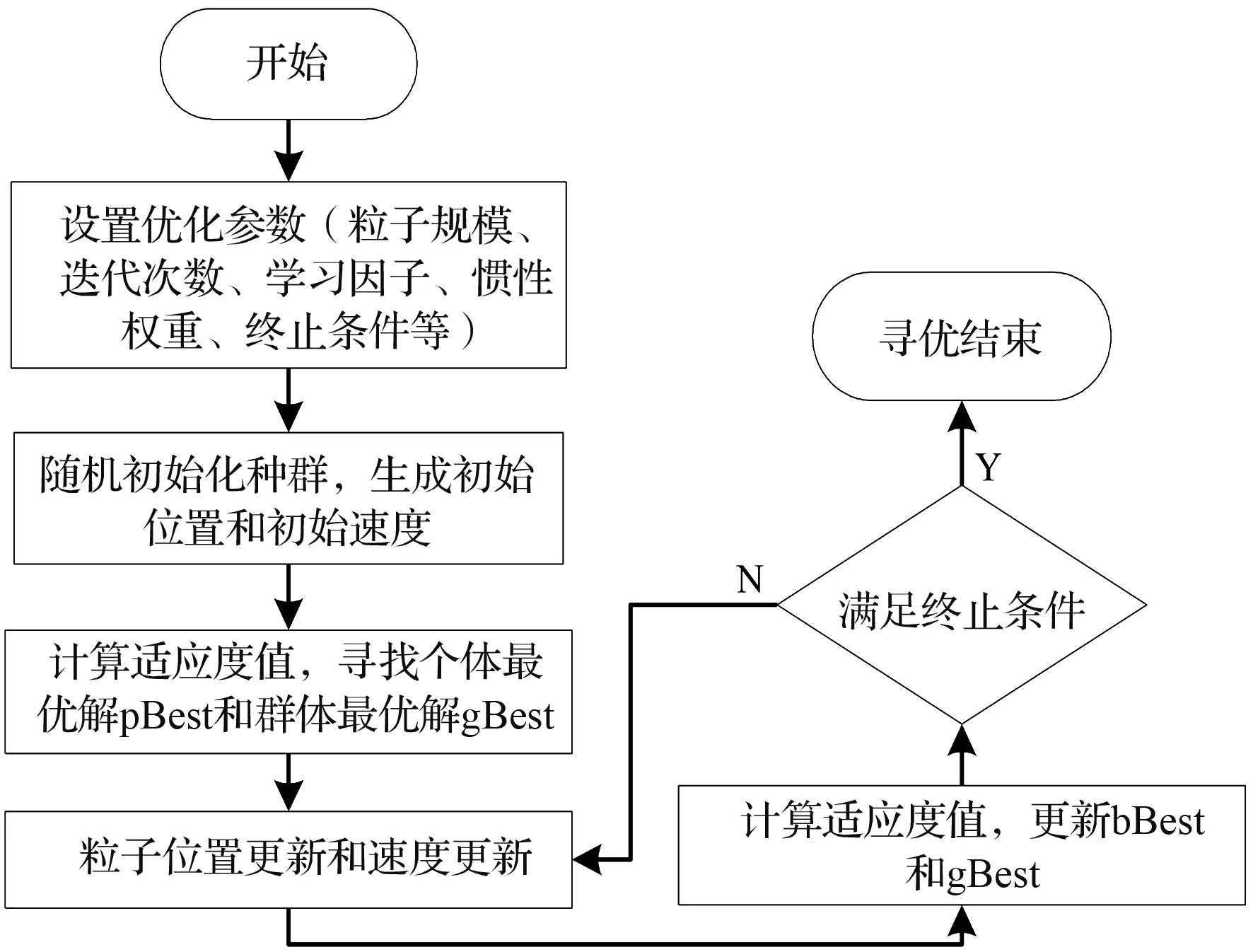
Fig.7 Optimizing steps of PSO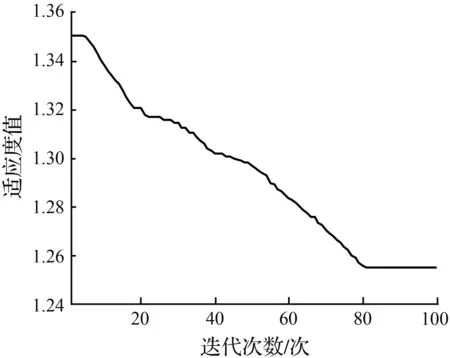
Fig.8 Convergence curve of fitness value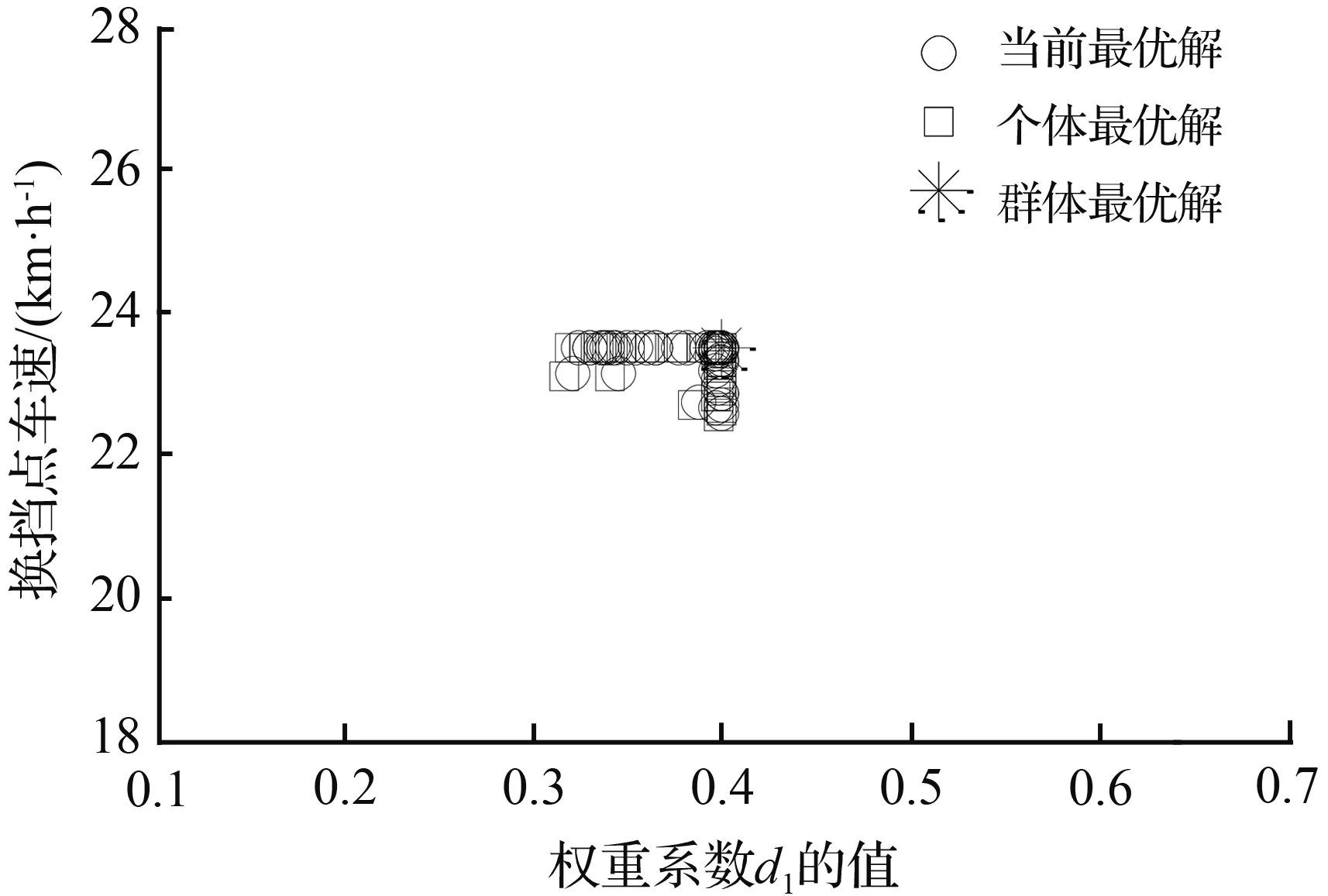
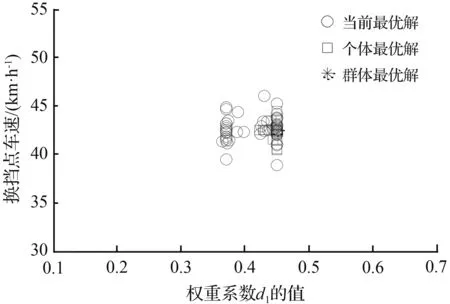
4.5 优化结果对比分析
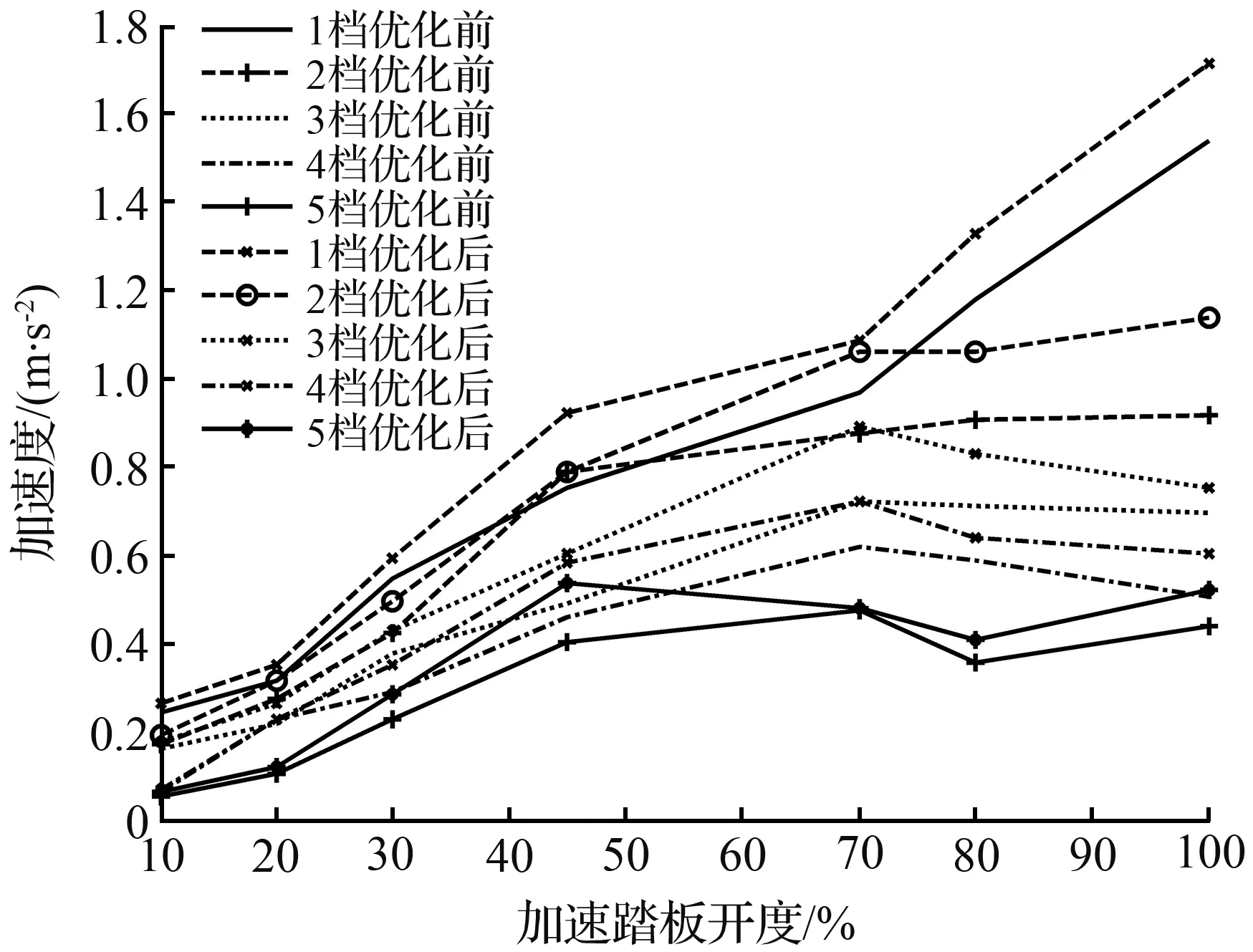
Fig.11 Dynamic index values beforeand after optimization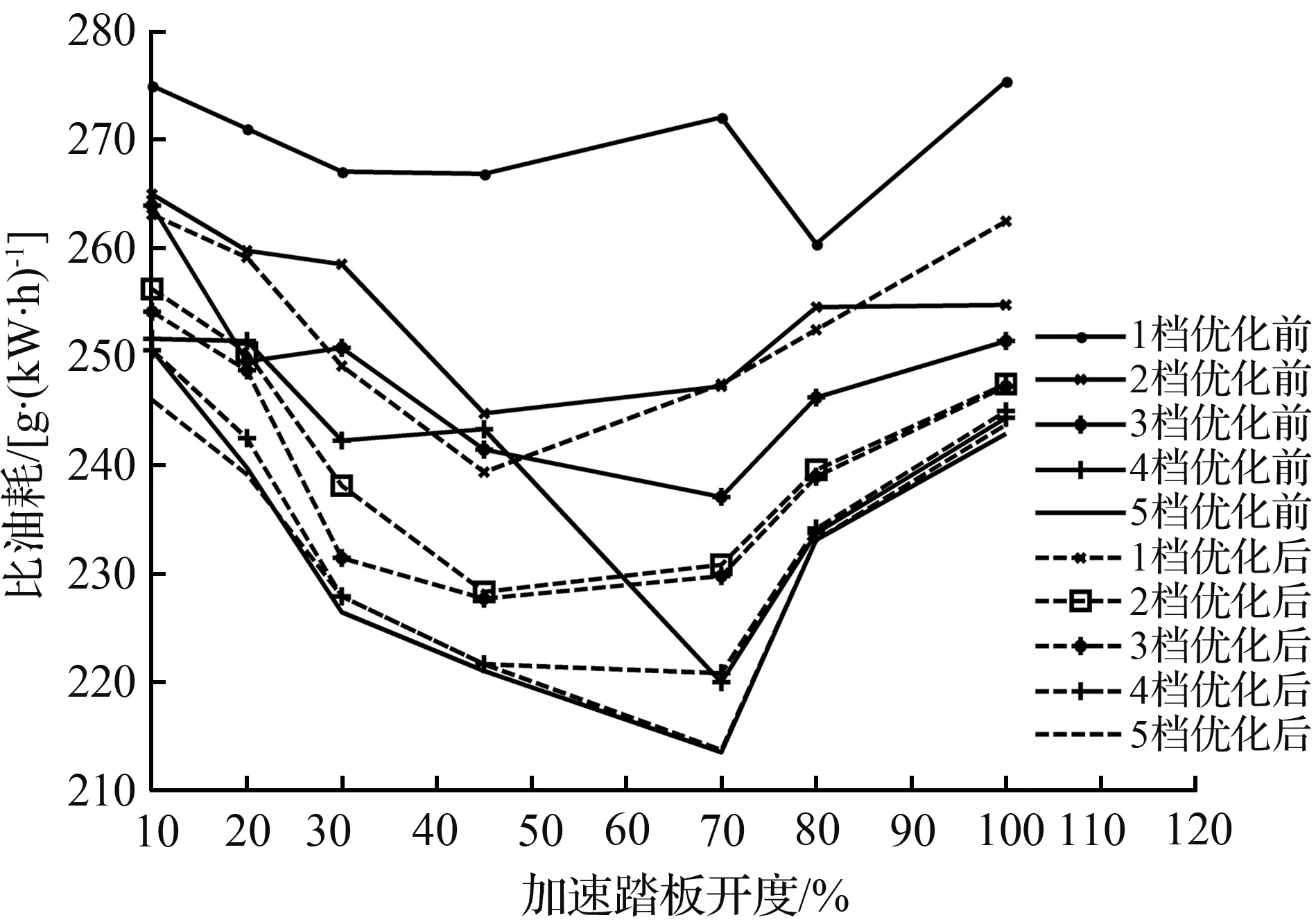
Fig.12 Economic index values beforeand after optimization5 结论
