四边形网格与三角形网格模型间的低频谱姿态迁移

(1.广西大学计算机与电子信息学院, 广西南宁530004;2.广西电网有限责任公司信息中心广西南宁530023)

在计算机图形学领域中常用多边形网格模型表示各种几何形状,主要包括三角网格和四边形网格。三角网格模型发展成熟、应用广泛,是最常用的三维几何模型表示方法之一。四边形网格模型也是一类重要的三维几何模型表示方法, 在机械制造、考古、医学、计算视觉等领域有广泛应用。与三角形网格相比，四边形网格更符合人类的视觉感知，在计算精度、计算效率等方面均优于三角形网格，更适用于CAD/CAM、纹理合成、计算机动画以及数值仿真等领域[1-4]。

模型变形编辑是数字几何处理的主要内容之一,也是提升几何模型设计效率的重要途径之一[5]。很多时候,需要按照指定的参考姿态进行变形使之具有与参考模型相似的姿态。作为基于样例的建模技术,变形迁移[6-9]提供了这一可能,它将模型的形变信息传递至源网格模型,使之作相似的变形,最终得到具有与参考模型相似的姿态。与变形迁移相比,谱姿态迁移仅仅需要输入参考模型的一个姿态,极大地扩展了基于样例的建模技术的应用范围。

三维网格模型的谱分析技术,揭示了拉普拉斯矩阵的特征向量的系数与网格模型的形状之间的联系[10-15]。Lévy等[16]将源网格模型和参考网格模型用各自的调和基展开,通过交换低频系数实现谱姿态迁移。Kovnatsky等[17]通过输入两组对应函数,采用联合近似对角化算法求解出两组近似等距对应的准调和基来解决姿态扭曲的问题。Yin等[18]在以上工作基础之上,一方面结合Laplacian编辑算法[19-20],建立了保细节的谱姿态迁移框架;另一方面,把参考姿态看作是一个分层结构的,将局部姿态(中高频姿态)转化为全局姿态(低频姿态),并对局部区域应用同样的谱姿态迁移方法,形成了分层谱姿态迁移框架。

但是,目前谱姿态迁移建立在三角网格模型的拉普拉斯矩阵的特征分解基础之上,主要在三角网格模型之间进行。

本文在三角网格模型谱姿态迁移的基础之上,研究并实现了四边形网格模型与三角形网格模型间低频谱姿态迁移。首先引入多边形网格模型的拉普拉斯矩阵,并对多边形网格模型的光顺[21]和重构进行了代码实现。其次,在多边形网格模型的情形下讨论了泛函映射和网格模型的特征对应,并对泛函矩阵、调和基以及耦合准调和基进行了可视化。最后,在多边形网格模型上分别设计并实现了平凡的谱姿态迁移、基于耦合准调和基的谱姿态迁移和基于拉普拉斯坐标投影的低频谱姿态迁移。

1 拉普拉斯矩阵及其特征分解

Alexa等[22]在一般多边形网格模型上构造了拉普拉斯矩阵,包括非凸多边形和非平面多边形的情形,为本文研究多边形网格模型谱姿态迁移提供了坚实的理论基础。本文正是在以上工作基础上研究多边形网格模型谱姿态迁移。本文所使用的多边形网格模型主要是三角网格模型和四边形网格模型。

1.1 拉普拉斯矩阵的谱与特征向量

若Lφi=λiφi(i=0,…,|V|-1),且φi≠0,则λi和φi为矩阵L的特征值和其对应的特征向量。对矩阵L作广义特征分解LΦ=M0ΦΛ便可以求出其全部特征值及其对应的特征向量,并假定特征值及对应的特征向量按照特征值的大小从小到大进行排列,其中Λ=diag{λ0,λ1,…,λ|V|-1},Φ={φ0,φ1,…,φ|V|-1}。这些全体特征值就是拉普拉斯矩阵L的谱,特征向量被称为网格M的调和基。同理,也可以对L作广义特征分解。但因其存在对称性,故其特征向量彼此正交。

1.2 多边形网格模型的Laplace光顺算法

Laplace光顺算法[21]是三角网格模型处理领域中的经典算法。文献[22]的算法能够被无缝迁移到多边形网格模型上。如图1所示,最左边为四边形网格模型Fertility, 依次向右为对其进行多次Laplace光顺的结果。

图1 四边形网格的Laplace光顺Fig.1 Laplace smoothing of the quad mesh

1.3 多边形网格模型重构

文献[16]将网格模型投影到拉普拉斯矩阵的特征向量上,并用基函数将其展开,即:

(1)

如图2所示,左一为原模型,该模型有10 493个顶点,从左2依次向右分别为使用20、50、100和300个调和基对原模型进行重构。

图2 网格重构Fig.2 Mesh reconstruction

2 耦合准调和基

在很多应用中,涉及到两个模型之间的对应关系。Ovsjanikov等[23]提出了泛函映射的方法,为研究两个模型之间的对应关系提供了新的手段。文献[17]在此基础之上,提出了耦合准调和基。

2.1 耦合准调和基的原理

图3 调和基可视化Fig.3 Visualization of the harmonic bases

图4 耦合准调和基可视化Fig.4 Visualization of the quasi-harmonic bases

2.2 多边形网格模型的特征对应

文献[17]通过优化调和基以得到两组新的耦合准调和基,从而克服了调和基表达不一致的问题。但是,耦合调和基的计算依赖于两个模型的特征对应关系,需要构造对应函数,并利用联合近似对角化算法求解。在本文中,通过手动选择对应点的方式构造k-邻域指示函数作为两个模型之间的对应函数,如图5(a)所示。如图5(b)所示,右半部分是耦合准调和基的泛函矩阵的可视化,左半部分是调和基的泛函矩阵的可视化,耦合准调和基的对角化程度明显比调和基高。

(a) 模型之间的对应顶点 (b) 泛函矩阵可视化

设在源模型M和参考模型M′上选取的p组对应顶点的集合为P={(v0′,v0),…,(vp′,vp)}。相应地,这两组对应函数可设为F={f0,…，fp}和G={g0,…，gp}，其中:

注意,本文是在多边形网格情形下讨论网格模型特征对应,包括三角网格和四边形网格,故顶点集合Nik′可以统一表示为顶点vi′的k-邻域中所有顶点构成的集合。集合Nik的表示与此类似。如图6所示,空心顶点构成的集合为实心顶点vi的1-邻域,其他情形与此类似。

图6 顶点vi的邻域1邻域Fig.6 One-ring neighborhood of the vertex vi

3 多边形网格模型谱姿态迁移

在以上基础之上,本文将文献[16]提出的平凡谱姿态迁移和文献[17]提出的基于耦合准调和基的谱姿态迁移扩展到多边形网格模型上,并给出相应的实验结果。

3.1 平凡的谱姿态迁移

根据前面拉普拉斯矩阵及其特征分解等有关理论可知,低频系数编码了网格的整体姿态,而高频系数则编码了网格的局部细节。文献[16]通过交换两个网格的低频系数的方式实现了姿态迁移,使得源网格模型与参考网格模型具有相似的姿态,同时保持源网格自身的细节特征。本文将这一方法应用到多边形网格模型上,实现了多边形网格模型谱姿态迁移。

(2)

(a) 参考网格 (b) 源网格 (c) 目标网格

谱姿态迁移依赖于两组一致表达的调和基。但事实上,在大多数情况下调和基是非等距对应的,调和基也因此往往表达不一致。正是此原因导致平凡谱姿态迁移在网格不等距对应的情况下出现姿态扭曲等情况,详见文献[17]。

3.2 基于耦合准调和基的谱姿态迁移

将基于耦合准调和基的谱姿态迁移扩展到多边形网格模型上,并给出两类实现方法,即基于笛卡尔坐标投影的谱姿态迁移和基于拉普拉斯坐标投影的谱姿态迁移。

3.2.1 基于笛卡尔坐标投影的谱姿态迁移

耦合准调和基克服了调和基在非等距对应的情况下表达不一致的问题。为此,可用耦合准调和基替换调和基以解决平凡谱姿态迁移所存在的姿态扭曲等问题。

(3)

(a) 参考网格 (b) 源网格 (c) 目标网格

(a) 参考网格 (b) 源网格 (c) 目标网格

(a) 参考网格 (b) 源网格 (c) 目标网格

(a) 参考网格 (b) 源网格 (c) 目标网格

3.2.2 基于拉普拉斯坐标投影的谱姿态迁移

Lévy等[16]在文献中提到另一种谱姿态迁移实现的途径,即将局部坐标投影到调和基上,例如拉普拉斯坐标。作者认为,对于大尺度形变的姿态迁移,通过投影局部坐标实现姿态迁移的方式更合适,而不是直接投影笛卡尔坐标。但是,作者并没有给出具体的实现步骤。

通过投影局部坐标的方式实现姿态迁移需要解决如何从新拉普拉斯坐标恢复出笛卡尔坐标。由于拉普拉斯矩阵是半正定的,因此从拉普拉斯坐标恢复出笛卡尔坐标需要额外的约束条件。本文结合拉普拉斯编辑算法[19-20],采用固定顶点位置的约束方法实现从局部坐标恢复出欧氏坐标。

设源网格模型M和参考网格模型M′的拉普拉斯坐标分别为:

δ=LMV=(δo,δ1,…,δ|V|-1)T,δ′=LM′V′=(δ0′,δ1′,…,δ|V′|-1′)T。

(4)

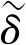
设M的固定顶点集合Vc={vc0,vc1,…,vcm}。通过约束固定顶点的位置,则有下面的能量函数:

(5)

(a) 参考网格 (b) 源网格 (c) 目标网格

4 实验结果与分析

为了说明本文工作的正确性和有效性,本文进行了不同类型的实验,并对实验结果进行说明和分析。

图7和图8分别展示了两个具有相同连接关系的同一三角网格模型不同姿态之间的平凡谱姿态迁移和基于耦合准调和基的谱姿态迁移。可以看出本文方法能够迁移模型的低频姿态(全局姿态)，但局部姿态没有被迁移, 如图7所示,目标网格的尾巴并未像参考姿态那样弯曲。

图9和图10分别展示了相同对象和不同对象的三角网格模型与四边形网格模型之间的低频谱姿态迁移。局部姿态(中高频姿态)没有学习到, 尾巴弯曲程度学习不充分。

图11展示了两个具有相同连接关系的同一四边形网格模型不同姿态之间的谱姿态迁移。目标网格较好地学习了参考模型的姿态。

图12展示了两个不同对象不同连接关系的三角网格模型之间的姿态迁移。模型的细节特征未随姿态变化而做相应地旋转,导致细节丢失,如图12所示,目标网格左前腿较为扁平。

5 结语

本文在文献[16-17]工作的基础之上,研究多边形网格模型谱姿态迁移,使其能够操纵更多类型的网格模型,主要包括三角网格模型和四边形网格模型。此外,也给出了四边形网格光顺和重构的实验结果。实验结果表明,本文姿态迁移方法能够操纵三角网格模型和四边形网格模型。但是仅限于低频姿态的迁移，而且所采用的保持源模型的细节方法需要计算网格模型的拉普拉斯矩阵的大量特征值与特征向量，当模型顶点数较大时，运算量很大，计算耗时较严重。

以后的工作将从两方面展开：一方面尝试新的保持目标网格的细节特征的方法，避免计算模型的拉普拉斯矩阵大部分甚至全部特征向量;另一方面采用分割手段,尝试建立起四边形网格分层谱姿态迁移框架,以解决局部姿态丢失的问题。