压缩感知波束形成算法性能分析

魏 娟，孙 健，邵 丁，闫 豪，李争光

（1.西安科技大学 机械工程学院，西安 710054；2.宝鸡吉利发动机零部件有限公司，陕西 宝鸡 721000）

波束形成声源识别技术由于具有测量速度快、计算效率高、中高频分辨率好、适宜中长距离测量等优点被广泛应用到航空、列车、汽车等领域[1]。延时求和[2-4]、互谱成像函数[5-6]等传统波束形成(Conventional beamforming，CB)算法虽然具有计算速度快、测量距离远、易于布置等优点，但其“主瓣”过宽造成空间定位精度低，“旁瓣”既高又多导致出现许多“鬼影”声源，因而限制其进一步的应用[7]。因此，各种提高波束形成算法识别效果的改进方法应运而生。

褚志刚[7]提出奇异值分解波束形成声源识别方法，突破了主声源最大旁瓣水平的限制，提高了识别次声源的准确度，进行了汽车前围板隔声实验；随后基于传统波数形成及矩阵特征值分解理论，提出函数波束形成方法，提高了识别分辨率，并且能够清晰地识别弱源，提出指数一般取为16的建议；黎术[8]提出了函数广义逆波束形成方法，在准确识别声源强度的基础上，通过增加阶次，成倍提高了算法抑制旁瓣能力；陈思[9]基于高阶矩阵函数提出了广义逆波束形成的改进算法，得到了阶次的最优区间，具有更高的声源识别精度。

压缩感知是近年来极为热门的研究前沿，在若干应用领域中都引起瞩目。其采用随机抽样的方式完成对目标信号的重建，打破了奈奎斯特抽样定理的限制，大大提高了信号处理速度。为了进一步提高波束形成算法的识别精度，降低算法的运行时间，将压缩感知的信号重构算法引入到波束形成中，提出了一种基于贪婪算法的压缩感知波束形成算法。通过数值仿真分析，分别以单极子和相干声源作为研究对象，运用仿真实验验证了压缩感知波束形成算法的正确性。

1 基本原理

压缩感知的理论主要由以下3部分构成：一是可压缩信号的稀疏表示，二是观测矩阵的构建，三是信号重构算法。

信号的稀疏表示就是将信号投影到正交变换基时，绝大部分变换系数的绝对值很小，所得到的变换向量是稀疏或者近似稀疏的，可以将其看作原始信号的一种简洁表达，这是压缩传感的先验条件，即信号必须在某种变换下可以稀疏表示，通常变换基可以根据信号本身的特点灵活选取，常用的有离散余弦变换基、快速傅里叶变换基、离散小波变换基、Curvelet基、Gabor基以及冗余字典等。

压缩感知中常用的测量矩阵有随机高斯测量矩阵，随机伯努利测量矩阵，部分哈达玛测量矩阵，部分傅里叶测量矩阵，稀疏随机测量矩阵等，这些矩阵都需要满足有限等距性（Restricted Isometry Property，RIP）。

压缩感知的重构算法很多，其中正交匹配追踪（OMP）算法被广泛使用。基于压缩感知OMP算法对波束形成算法进行改进，使其在分辨率与运行时间上有较大改善。

2 模型分析

如图1所示，将空间声源面分成N份，在其上分布着K个同频相干声源，其位置坐标为Sn（xn，yn，zn），在测量面上分布着M个均匀分布的传声器阵列。

声源信号是自然空间稀疏信号，将信号与其空间所在位置一一对应，传声器阵列接收信号并重构声源发射信号，为声源定位提供基础。

图1 声源测量模型

2.1数学模型

给定具有M个传声器组成的测量阵列，输出y=(y1…yi…yM)T∈RM×1，(·)T代表转置，对于在空间中传播的声源信号用x(t)∈R1表示，根据相关格林函数，波束形成的输出为

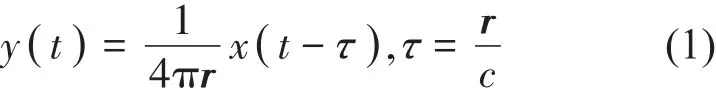
r是声源到传声器的距离，rϵRM×1;t是声音传播时间，τ是相应的传播时间时延。

在实际应用中，波束形成一般在频域内进行，式（1）相应的频域方程为

对于具有多个信号和受测量噪声影响的问题，情况变得更加复杂，数组输出以标量形式表示为

其中：Aik表示第i号传声器与第k个信号之间的导向矢量，Xi表示第i个信号，Ni表示第i号传声器总的测量噪声包含了数据采集期间的背景干扰和电子噪声。为简洁起见，方程式（4）可以写成

A为M×N维感知矩阵，n为传声器阵列接收的噪声信号，该模型描述的问题实质上是利用已经获知的感知矩阵A和传声器测量的信号y来重构稀疏信号x的过程。

2.2 OMP算法流程

输入为：

（1）M×N的传感矩阵A=Φψ；

（2）N×1维观测向量y；

（3）信号的稀疏度K。

输出为：

OMP算法流程为

（2）找到索引λi，使得

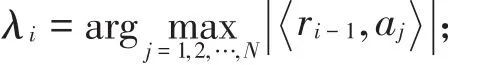
（4） 求y=Aiθi的 最 小 二 乘 解

（3）令∧i=∧i-1∪λi,Ai=Ai-1∪aλ；

（6）t=t+1，如果t≤K则返回第(2)步，否则停止迭代进入第(7)步；

（7）重构所得在∧i处有非零项，其值分别为最后一次迭代所得

其中：ri表示残差，t表示迭代次数，Φ表示空集，∧i表示t此迭代的索引集合，λi表示第t次迭代找到的索引，aj表示矩阵A的第j列，Ai表示按索引∧i选出的矩阵A的列集合，θi为t×1的列向量，符号∪表示并集，表示向量内积。

信号的稀疏度可由下式得出

2.3 OMP算法的信号重建

以一维信号为例验证OMP算法的重建效果。假设稀疏信号x长度N=256，观测值个数M=64，取稀疏度K=10，取满足有限等距性的随机高斯矩阵为测量矩阵Φ，取单位矩阵为稀疏矩阵，利用MATLAB得到的恢复信号如图2所示。

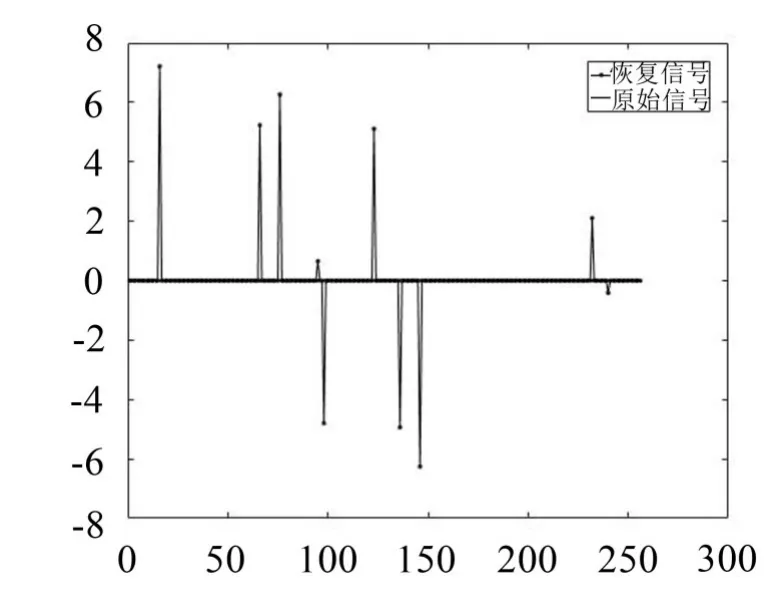
图2 OMP算法信号恢复图

恢复残差为4.3963×10-15，可以证明OMP算法可以完美恢复原始信号。

3 数值仿真分析

将测量平面离散成点间距为0.025 m大小的离散平面，每个离散点均为压缩感知波束形成的聚焦点，在声源平面任意位置上布置单极子声源，与测量面的距离为1 m，单极子声源辐射声压为30 Pa，频率为2000 Hz。在测量面上布置7×7的正方形传声器阵列，间距为0.1 m，利用压缩感知波束形成方法和函数波束形成方法进行声源识别成像仿真对比。

3.1 单极子声源

在声源平面上布置单极子声源，位置坐标为（0 m，0 m，1 m），分别运用压缩感知波束形成方法和函数波束形成方法进行声源成像，结果如图3至图6所示。

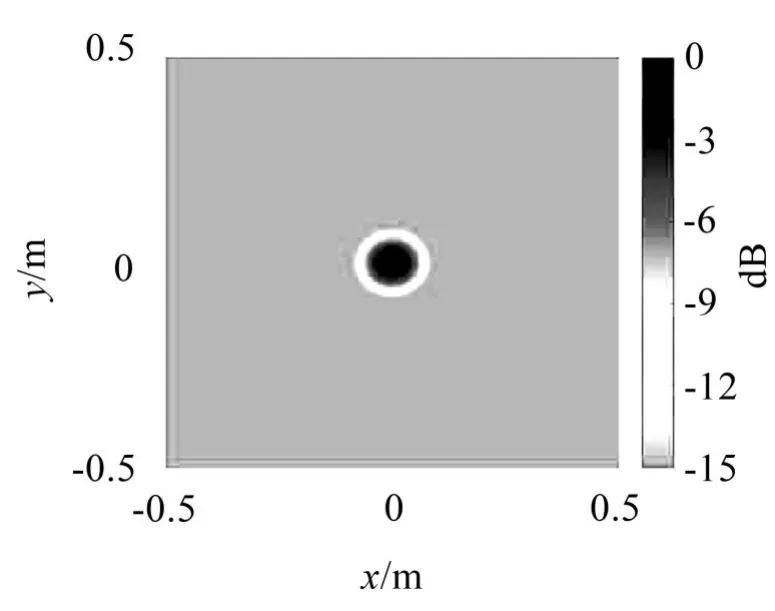
图3 函数波束形成二维识别图

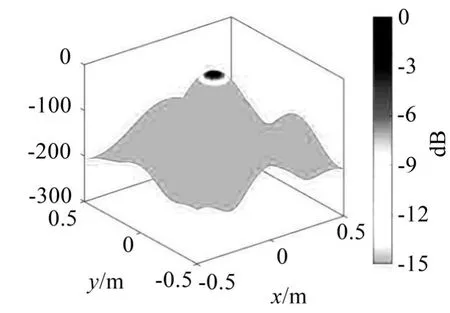
图4 函数波束形成三维识别图

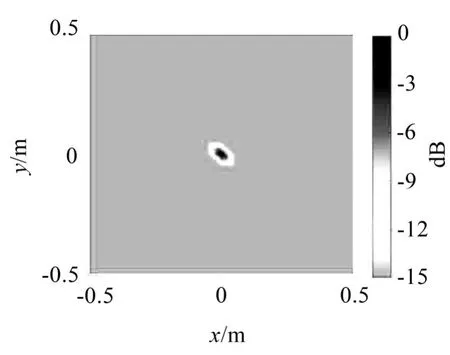
图5 压缩感知波束形成二维识别图

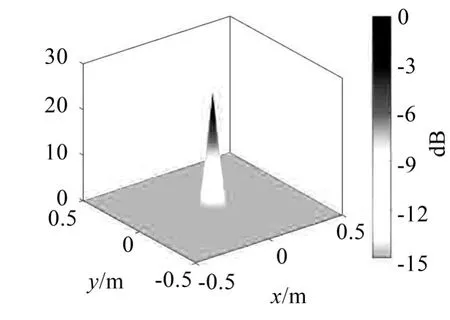
图6 压缩感知波束形成三维识别图

函数波束形成的运行阶次取16。仿真结果表明，压缩感知波束形成方法在识别声源的精度上和对于旁瓣的抑制上都优于函数波束形成算法。

压缩感知波束形成方法和函数波束形成方法对于单极子声源的运行时间如表1所示。

表1 单极子声源两种算法运行时间对比/秒

根据表中数据可以得到，对于单极子声源的识别，压缩感知波束形成方法的运行时间远小于函数波束形成运行时间。

3.2 相干声源

在声源平面上布置两个相干声源，位置坐标分别为（-0.3 m、0 m、1 m）和（0.3 m、0 m、1 m），分别运用压缩感知波束形成方法和函数波束形成方法进行声源成像，结果如图7至图10所示。

函数波束形成的运行阶次取16。仿真结果表明，压缩感知波束形成方法在识别声源的精度上和对于旁瓣的抑制上都优于函数波束形成算法。

压缩感知波束形成方法和函数波束形成方法对于相干声源的运行时间如表2所示。

表2 相干声源2种算法运行时间对比/秒

根据表中数据可以得到，对于单极子声源的识别，压缩感知波束形成方法的运行时间远小于函数波束形成运行时间。

4 结语

（1）本文将压缩感知中贪婪算法与波束形成方法相结合，提出了一种压缩感知波束形成方法，通过理论分析，探究了对于单极子声源和相干声源压缩感知波束形成算法对声源的识别效果。

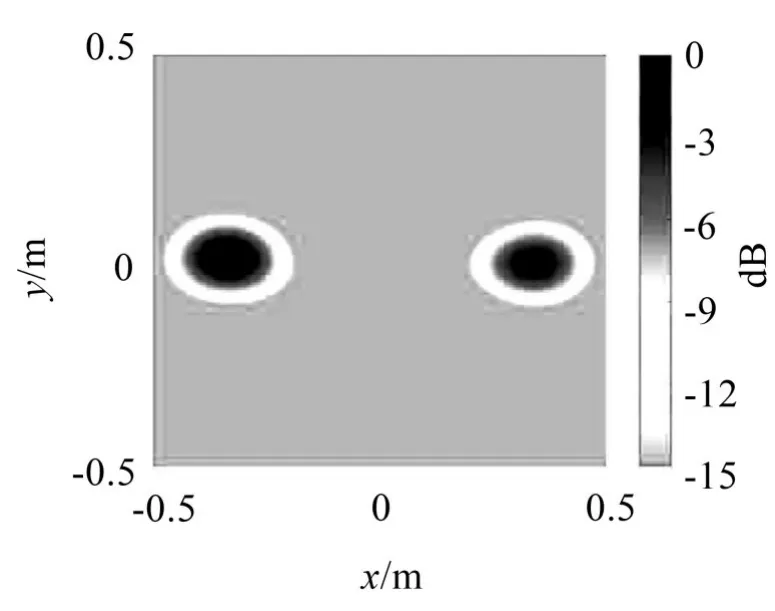
图7 函数波束形成二维识别图

图8 函数波束形成三维识别图

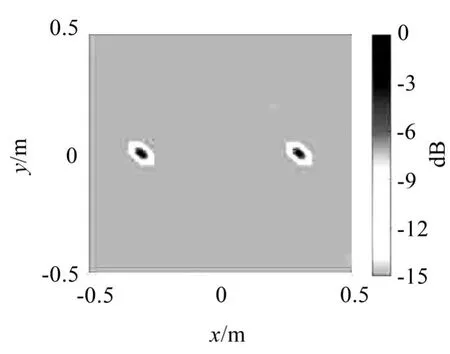
图9 压缩感知波束形成二维识别图

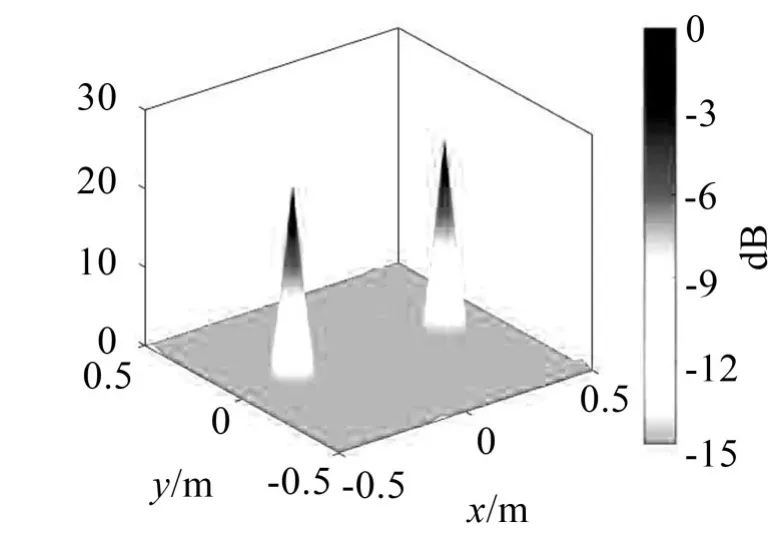
图10 压缩感知波束形成三维识别图

（2）对比压缩感知波束形成方法与函数波束形成方法，数值仿真结果表明压缩感知波束形成方法在声源识别的准确度、对于旁瓣的抑制能力和识别时间方面具有更优越的性能。