异步电机静偏心状态电磁激励力的建模分析与实验研究

陆 翔，蒋伟康

（上海交通大学 机械系统与振动国家重点实验室，上海 200240）

电磁噪声是由电磁力激励电机定子铁心和机座振动向外辐射的噪声，降低电磁噪声的有效方法之一就是降低电磁力幅值和提高电磁力阶次频率；另外，定子振动的测量实验十分繁琐，若能准确计算电磁激励力，便能直接通过仿真计算获取定子的振动响应和辐射噪声，可见电磁力计算对于电机振动分析具有重要意义。电磁激励力是由于电机的定、转子气隙磁通相互作用而产生的随时间和空间变化的径向力波，而异步电机在运行过程中常常出现静偏心、动偏心或者三相不对称等问题，使电机处于不平衡运行状态，导致电机气隙磁场分布不均匀，进一步导致转子产生更大的偏心振动，可见电机的电磁振动是电机转子与气隙磁场相互耦合作用产生的复杂动力学行为。因此在确定电磁激励力前，有必要研究电机磁-固耦合动力学行为的机理。

电磁力的求解方法主要分为解析法和数值法，相关论文无论是求解谐波解析表达式[1]，还是采用有限元法计算时域波形图[2]，在计算不平衡电磁力时都没有考虑转子振动偏心对气隙磁场的影响，通常是直接采用初始的转子静偏心量以及电机电气参数，计算转子气隙磁场和径向电磁力，这种简化在电磁激励力与转子振动位移耦合程度较弱的情况可以接受，但其计算结果不能在本质上准确描述气隙磁场与转子结构场的磁-固耦合机理，尤其是在转子轴承较长、刚度较小的电机中，电磁激励力受到转子振动位移的影响较大，磁-固耦合程度较强，不平衡电磁力的计算结果与实际情况的误差会非常大。为了描述电机磁-固耦合动力学行为，2016年Chen和Xiang等[3-4]分别将不平衡电磁力视为激励力和等效弹簧因子，建立转子系统振动方程，并分析转子的非线性振动，但没有进一步揭示转子系统中影响不平衡电磁力的关键因素。

本文推导了转子-气隙系统的拉格朗日-麦克斯韦能量方程，建立了异步电机的磁-固耦合动力学模型，提出了静偏心状态下转子振动响应的数值计算方法，根据转子振动响应和气隙实际长度计算了各阶次不平衡电磁力谐波以及径向电磁力合力，通过实验验证了理论建模和数值计算的准确性，并研究了转子弯曲刚度及静偏心对于气隙磁场和电磁力分布的影响。本文提出求解电磁力的理论模型和数值计算流程，通过对受电磁力激励的转子动力学进行建模和数值计算，得到了实际气隙长度分布，与前人的电磁力计算方法相比，计算和预测精度提高了，其对低噪声异步电机设计具有参考价值。

1 电机磁-固耦合动力学建模

电磁力的幅值和频率是由气隙磁场决定的，而转子的横向弯曲振动会改变气隙长度，进而改变气隙磁场密度，因此将转子和气隙视为一个磁-固耦合动力学系统，研究转子的横向弯曲振动规律。由于分析转子振动响应时只关心电磁力合力的作用效果，将转子简化为两端固支并与定子分离的Jeffcot转子模型，且由转子重量产生的静变形对转子运动的影响不显著。

用L0表示拉格朗日函数，转子-气隙系统的拉格朗日函数除了转子动能减去转子弯曲势能以外，还需加上气隙磁场能Wm。同时在方程中引入运行过程中由于结构阻尼损失的耗散函数，用Ψ表示。用t表示时间，q表示广义坐标，q′表示广义坐标一阶导数，Q′表示其它非有势力，在电机运行过程中主要为电磁阻尼力。最终得到包含耗散函数的拉格朗日-麦克斯韦方程。

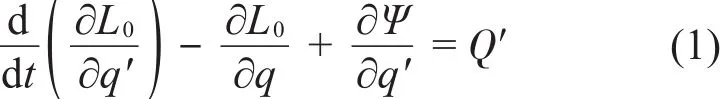
在定、转子铁心横截面上建立坐标系，如图1所示。

图1 转子横截面坐标

将转子圆心的坐标设为o′( )X,Y，e为电机初始静偏心，δ0为均匀气隙长度，α为指定气隙的周向方位角，α′为气隙最小处的周向方位角。由于定子与转子轴承分离，可以认为定子仅受电磁力作用并且是固定在机座上的刚性体，简化中忽略了定子铁心的微小振动，在偏心状态下，圆周上任意方位角α处的气隙长度大小为

根据电磁学，当空间磁介质满足线性条件以及无磁滞损耗时，对于任意传导电流分布情况，空间磁场能体积分公式可以表示为

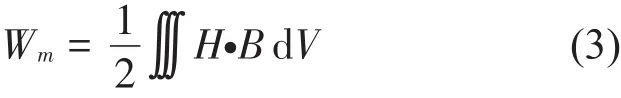
其中：H为磁场强度，B为磁感应强度。由于气隙中磁场能以基波成分为主，方程式(1)中拉格朗日函数的磁场能采用基波磁场能近似。为了能在整个转子铁心圆柱体上用麦克斯韦理论积分求解磁场能，需要做出以下假设：

（1）忽略异步电机的端部效应，轴向磁通有畅通磁回路，即电机沿轴向的磁场不会改变；

（2）忽略转子偏心对气隙磁场磁感线分布的影响；

（3）定子与转子轴承分离，定子铁心的微小振动可以忽略。基于上述假设，异步电机的气隙磁场能可以通过推导得到

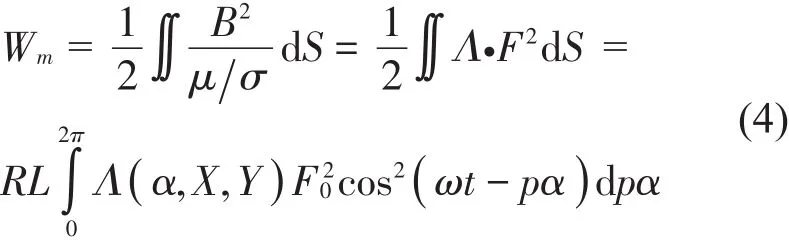
其中：μ为磁化介质的磁导率，Kμ为磁路饱和系数与卡特系数之积，σ=Kμ×δ为实际气隙的有效长度，R为转子半径，L为转子铁心长度，p为电机极对数，ω为电源角频率，基波气隙磁导Λ以及气隙磁势幅值F0可以分别通过式(5)、式(6)求得

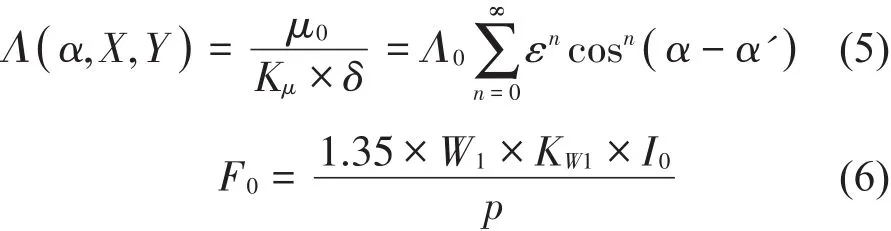
式(5)中μ0为磁化气隙的磁导率，令σ0=Kμ×δ0为气隙有效均匀偏心，则ε为转子静偏心与气隙有效均匀偏心的比值；式(6)中W1为定子每相绕组匝数，KW1为定子绕组系数，I0为激磁电流，可通过实验以及电机等效电路T型图和矢量图求得。对式(5)可以进一步进行泰勒展开以及三角函数积化和差推导，并展开为X、Y的表达式，通常级数展开到第4项(取n=4)，此时磁导精度足够高。将式(5)和式(6)代入式(4)，对方位角α从0到2π进行积分，得到Wm(t,X,Y)的表达式

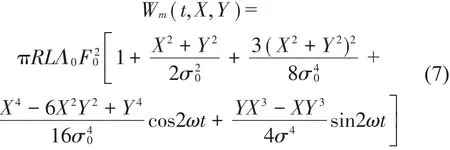
方程式(1)中电磁阻尼力Q′相对于电磁激励力幅值而言要小2到3个数量级[5]。令极对数p为2，将式(7)代入方程式(1)，经过推导得到X、Y方向的无量纲振动方程分别为

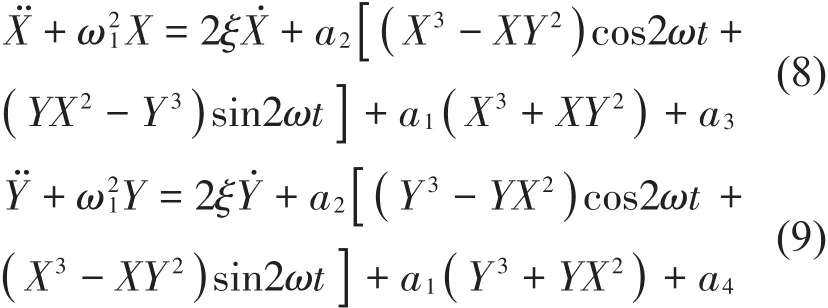
式(8)和式(9)是一组力学变量与电磁学变量相互耦合的非线性振动方程组。其中初始条件为和令m为转子系统质量，K为转子系统弯曲刚度，c为转子系统结构阻尼，可得上式中各参数的表达式

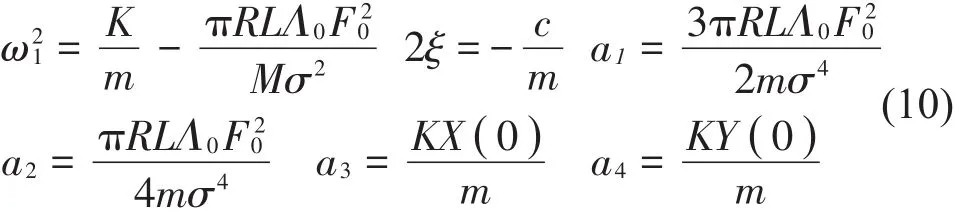
振动方程解的基频为ω1，电磁力作用在转子上产生负刚度效应，会减小转子主轴系统的弯曲刚度[6]，且基频随着气隙磁势和磁导的增大而减小，同时基频也与转子主轴系统自身的弯曲刚度有关。当基频接近参数激励频率的一半时，系统发生参数共振。

本文主要研究电机转子在静偏心状态下具有磁-固耦合关系的非线性方程组，将电机实际的电磁参数和结构参数代入式(8)和式(9)。为获得迭代计算的初始条件，根据气隙磁场能量法，通过对气隙磁场能表达式（4）求偏导得到径向电磁力合力表达式，以X轴方向电磁力为例

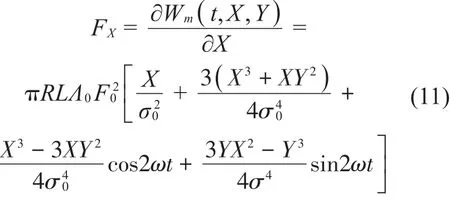
X、Y方向分别代入初始条件，计算初始径向电磁力合力，作为转子有阻尼系统的简谐力激励项，不考虑气隙长度与电磁力的耦合关系以及非线性因素，建立转子的线性强迫振动化方程如下

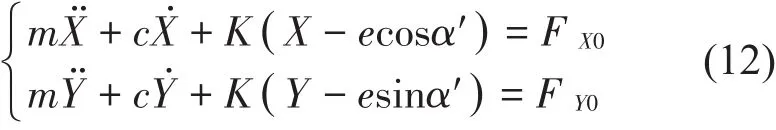
求解线性振动方程可得到实际非线性方程的优化初始条件。已知式（8）和式（9）的位移、导数的初值，可以采用4阶龙格库塔法进行迭代计算，调整迭代的步长，满足截断误差不大于1×10-5m，且算法处于绝对稳定区间中，避免步长过小而浪费计算资源。在得到气隙实际长度的周向分布后，进一步计算不平衡电磁力，并结合数值解分析转子振动响应规律及电磁力影响因素。

2 不平衡电磁力分析

根据麦克斯韦应力张量法，由电机气隙磁场产生并作用于定、转子铁心表面上的单位面积径向电磁力为

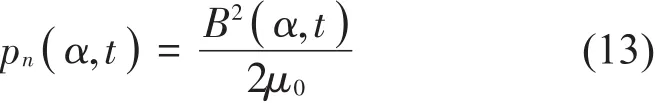
其中：μ0=4π×10-7H∕m为真空磁导率，B为气隙磁场密度，在正常运行的三相异步电机中，当忽略磁场饱和因素时，气隙磁密等于气隙磁导与磁势的乘积。气隙磁导与磁势除了主要基波成分以外，同时也有定、转子绕组的各阶谐波成分

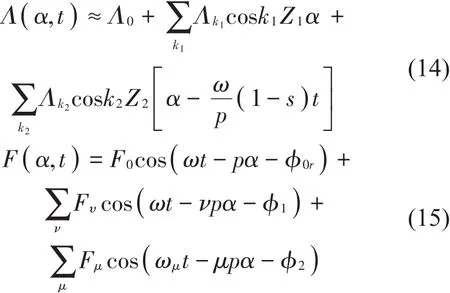
其中：k1、k2为一系列正整数，Z1、Z2分别为定、转子铁心槽数，s为转差率，ν、μ分别为定、转子谐波阶数，φ0r、φ1、φ2分别为激磁电流、定子电流、转子折算电流在电机矢量图中的相位角，ωμ为转子谐波旋转角速度。定、转子谐波磁势幅值与式(6)相似，然而由于定子绕组受到绕组分布系数的影响，谐波磁势幅值会受到大幅削弱，仅对于满足νz=±6k1q+1（q为每极每相槽数）的定子齿谐波绕组，其绕组分布系数与基波相等，其齿谐波的磁势幅值不会被削弱，对于鼠笼式转子可同理进行分析。因此合成磁势时主要考虑基波以及定、转子的低阶齿谐波（k1=1、k2=1）。

式(14)与式(15)相乘，略去幅值较小的谐波成分，得到磁密的谐波表达式（16），其主要由基波、定转子磁导齿谐波以及定转子绕组齿谐波构成。其中定转子各自的磁导齿谐波与绕组齿谐波具有相同的频率、阶数，因此可以矢量叠加。

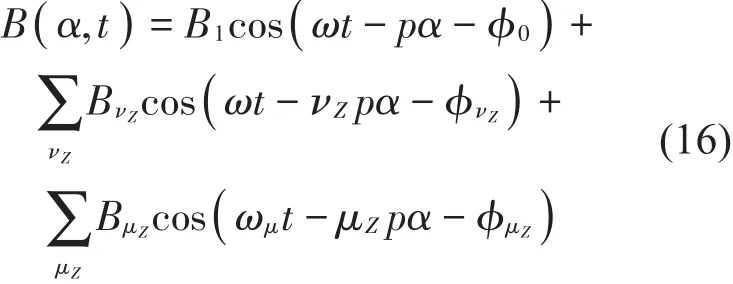
将式（16）代入式（13），并进行三角函数积化和差展开，由于展开项中非周期项分量以及阶次高、幅值小的力波分量对电机振动噪声的影响可以忽略，因此激励电机产生电磁振动的主要力波分量由2倍基频径向电磁力波构成，简化后表达式见式（17），其中第一项是由气隙磁场基波分量产生的径向电磁力波，第二项是由定子齿谐波和基波分量共同作用产生的径向电磁力波，两者无法消除，但可以削弱其幅值和改变电机结构固有频率从而避免发生共振。

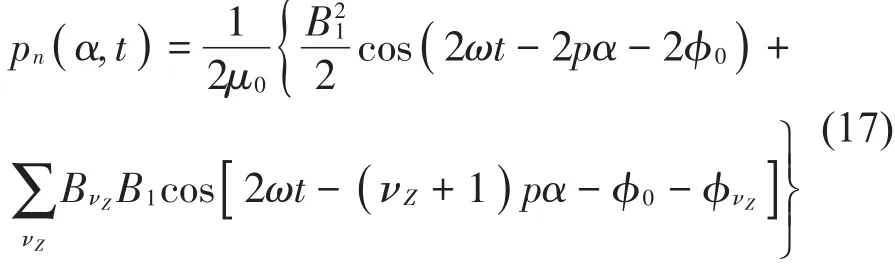
由式（5）和式（17）得知，气隙磁导与气隙长度成反比，气隙长度的变化将被平方放大后作用在电磁力幅值上。因此当电机运行出现不平衡状态时，气隙长度因为转子的振动响应而改变并产生振动偏心时，直接采用基于转子初始静偏心计算的电磁力误差将变大，应当考虑转子振动偏心对气隙长度周向分布的影响。

3 实验研究

选取型号为Y250m-4的实验特制异步电机进行实验，实验电机为了符合定子微振动简化条件，将定子与轴承座分离，定子和轴承座分别通过螺栓固定在刚性基础上，保证两者都具有足够的刚度，并通过一条长条形键进行连接和定位；采用无径向间隙的滚珠轴承，通过预紧消除轴承径向间隙，以减小由轴承径向间隙引起的转子静偏心和动偏心问题；要求转子所用的主轴两端直径尽量大，以便安装千分表，同时可以减小轴在离心力作用下的变形。电机极对数为4，定、转子槽数分别为48、38，定子内外径分别为260 mm、400 mm，转子内外径分别为85 mm、256 mm，均匀气隙长度达到2 mm，定转子槽口宽度分别为4 mm、1.5 mm。电机在三相对称的正常工况（380 V，50 Hz市电）下稳定空载运行，采用薄片Hall效应传感器测量气隙磁场磁感应强度，传感器埋置在定、转子之间的气隙中，采样频率为25600 Hz，并取其中0.4 s稳定运行时段的信号进行分析计算，间接得到径向电磁力。实验中以电机顶部定子铁心齿所在位置为1号齿，取逆时针旋转角为9π∕24处的齿为研究对象，在上面粘贴5个传感器，沿着铁心轴向均匀分布。所有机械、电磁信号通过一个多通道数据采集系统进入电脑分析系统，如图2所示。

图2 电机电磁实验结构及系统示意图

3.1 转子没有静偏心时的电磁力研究

没有静偏心的三相对称异步电机在运行过程中处于平衡状态，因而气隙长度不会发生改变，可以直接计算各阶电磁力波。空载运行过程中由于转子转速与同步转速近似相等，为1500 r/min，故转子电流近似为零，激磁电流近似等于定子空载电流，由实验测得定子空载电流为30.0 A。定子每相串联匝数W1为80，绕组系数为0.925。

根据式(6)计算得到基波磁势幅值为1498.5 A；根据定、转子槽口宽度计算半开口槽卡特系数为1.2102，由式(5)计算得到基波磁导为5.1919×10-4H。不考虑饱和时令饱和系数为1，计算基波与低阶谐波磁密幅值，结果如表1所示。

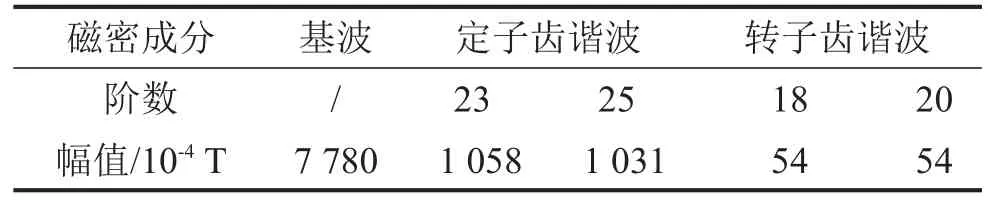
表1 磁通密度计算值

可见转子齿谐波幅值较小可以忽略。转子无静偏心情况下气隙磁密的谐波表达式如下

根据麦克斯韦应力张量法，不考虑频率为0的直流分量，得到

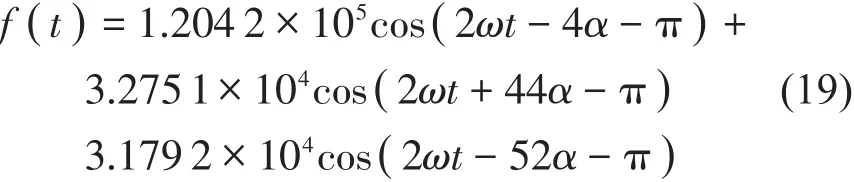
将实验结果与计算结果的频谱图进行对比，结果如表2和图3所示。

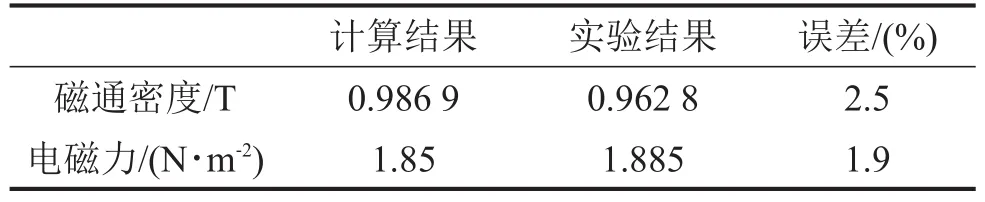
表2 计算结果

可知数值计算结果基本可以反映气隙磁场主要磁通密度和电磁力的幅值和频率，验证了电机平衡运行状态下电磁力计算过程的准确性，为进一步研究不平衡电磁力计算模型打下了基础。

3.2 转子有静偏心时的电磁力研究

通过垫高实验电机轴承座同时改变两端轴承中心位置，并结合非接触式位移传感器采集的信号来调节转子静偏心达到0.5 mm，测量磁通密度得到其主要幅值为1.166 T，频率为50 Hz，相应的径向电磁力幅值为2.748× 105N∕m2，频率为100 Hz。

建立气隙转子磁-固耦合动力学模型，转子横截面坐标轴见图2。

将垫高轴承后定子顶端气隙最小处定为x轴正方向，则振动方程问题得到简化，α′=0，偏心e=X()

0，同时由于转子横截面关于x轴对称，y轴方向上始终处于力平衡状态，因而令Y=0，代入式(8)，只需研究X轴方向的振动方程组。

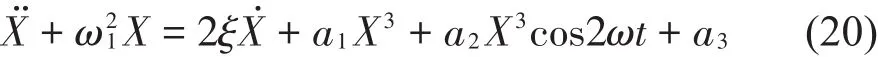
其中：ω1、ξ、a1、a2、a3与式(10)一致，转子系统总质量m=109.3292 kg，系统黏滞阻尼c≈163.9938 N/(m·s-1)。由于两端固支，不考虑支撑刚度，转子弯曲刚度可近似为中间主轴弯曲刚度，根据45号钢的弹性模量可以计算得到转子弯曲刚度为4.4277×107N∕m。

方程解的基频与激励频率的一半相差较大，因而不满足参数共振的条件。由于方程难以直接获得解析解，采用4阶龙格库塔数值法，按一定的时步长迭代计算转子的振动响应。为了加速迭代的速度，首先求解线性化振动方程，获得合适的初始条件。最后进行4阶龙格库塔数值计算。调整迭代的时步长为0.0005 s，经过验证时步长满足截断误差不大于1×10-5m的条件，并且处于4阶显式龙格库塔法的绝对稳定区间中。迭代计算过程收敛后，转子非线性系统振动响应主要包含幅值为9.06×10-4m的直流分量以及幅值为2.0×10-5m、频率为100 Hz的参激振动1阶谐波分量。

由于直流分量幅值比参激分量幅值大一个数量级，因此转子振动偏心e′可近似等于9.06×10-4m。那么可以计算得到方位角9π∕24处的气隙长度为1.6533 mm。在转子存在静偏心情况下测量的三相相电流基本保持不变，均值仍然为30.0 A，则根据电磁力幅值与气隙长度的关系，可以直接得到磁通密度和电磁力的数值解。采用传统方法直接代入初始静偏心0.5 mm计算磁通密度与电磁力，将两种方法数值解分别与实验值对比进行误差分析，如表3所示。

图3 频谱对比图

通过以上对比可以得出，异步电机在转子存在静偏心时，由于气隙磁场不对称使转子产生振动偏心，转子振动偏心又会改变气隙磁场的分布，采用初始静偏心直接计算电磁力误差高达17.8%，而通过求解转子非线性磁-固耦合振动方程得到气隙实际长度，电磁力数值解的误差减小为1.5%，误差大大缩减并符合工程应用要求。

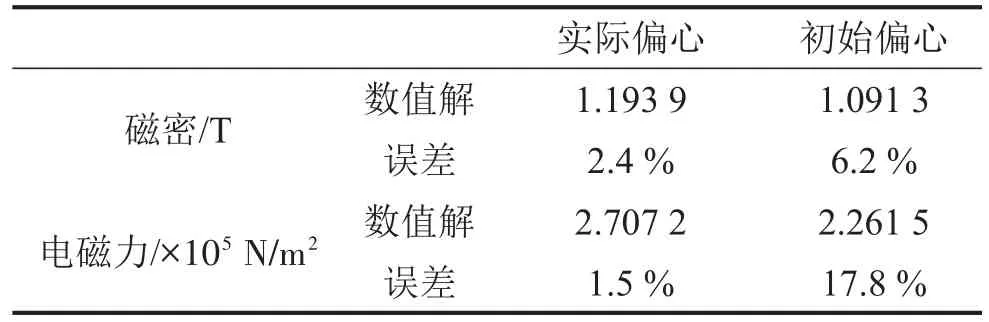
表 3误差对比

3.3 转子刚度和静偏心对径向电磁力合力的影响

基于本实验中三相对称空载运行电机的算例，首先固定转子静偏心数值以及其它参数不变，改变转子弯曲刚度大小并计算转子的振动响应，对结果进行频谱分析，其主要成分均为频率为零的直流分量和2倍电源频率的参激振动1阶谐波分量。各数值解见表4。

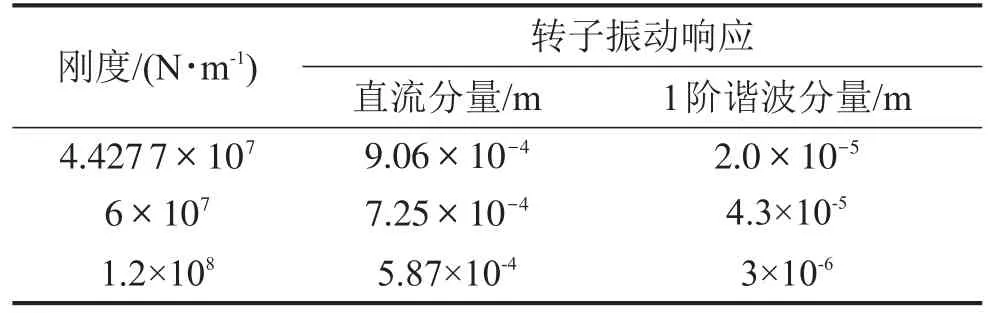
表4 转子刚度影响对比

一方面，弯曲刚度越小，振动偏心就会越大，气隙磁场周向分布不均匀程度和径向电磁力合力也都会相应越大。另一方面，非线性振动方程的基频大小与弯曲刚度有关，而基频越接近参数共振频率（ω、4ω等），参激振动谐波分量的幅值也会越大。

固定转子刚度以及其它参数不变，改变转子初始静偏心大小并计算转子的振动响应，对结果进行频谱分析，其主要成分同样均为频率为零的直流分量和2倍电源频率的参激振动1阶谐波分量。各数值解见表5。

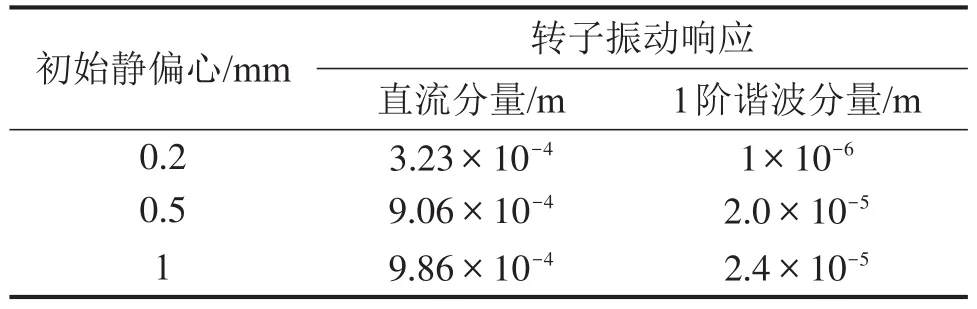
表5 转子初始静偏心影响对比

可见，静偏心初始值越大，转子振动响应的直流分量和参激振动谐波分量幅值就越大，相应的径向电磁力合力也会越大。

该数值计算中存在两个极限情况，一方面当转子初始静偏心为零时，转子不会产生振动偏心和涡动，此时径向电磁力合力为零；另一方面，当转子初始静偏心大于一定程度，数值计算结果不再收敛，此时转子在振动过渡过程中有可能与定子发生碰磨而损坏。

4 结语

建立了转子静偏心状态下的磁-固耦合动力学模型，主要考虑了转子振动偏心直流分量对气隙磁场的影响，采用4阶龙格库塔算法通过数值计算得到了实际气隙长度分布，提高了不平衡电磁力的预测计算精度，并通过实验验证了理论建模和数值计算的正确性。进一步分析了转子刚度和初始静偏心大小对电磁力的影响，指出转子刚度越小且初始静偏心越大，气隙磁场的周向分布就越不均匀，导致径向电磁力也就越大，同时转子参激振动谐波分量的幅值也与转子弯曲刚度相关；另外，从对计算结果频谱图和电磁力计算过程进行的分析可得，电机电磁力频率与转子弯曲刚度或初始静偏心均无关，而仅与电源频率相关。

本文的理论建模和数值计算过程适用于具有细长转子主轴、弯曲刚度较小的异步电机的不平衡电磁力计算，理论模型既考虑了转子结构和振动响应对气隙径向电磁力的影响，也考虑了气隙电磁激励力对转子系统的作用，相比于采用初始静偏心直接计算电磁力的传统方法，考虑了实际转子的振动偏心，提高了不平衡电磁力的计算和预测精度。