汽车驾驶性评价中小波去噪分解层数的确定

刘海江，张 欣，李 敏

（同济大学 机械与能源工程学院，上海 201804）

在汽车驾驶性评价过程中，由于测量过程中路面的不平坦、车身的振动、仪器本身及数据在传输过程中会受到诸多因素的影响，测量的数据中必然会存在噪声干扰，导致评价指标计算不准确，进而影响到驾驶性能的评价，因此在驾驶性评价之前需要进行含噪数据的处理[1-2]。随着信号处理技术的发展，小波变换在数据处理中的应用越来越广泛。由于汽车驾驶性评价过程中的测量数据一般都为离散数据，因此可采用离散小波去噪，对测量信号进行相应的分解与重构，小波去噪可有效地分离出异常信号，保留有用的信号信息。但是在进行小波去噪时，小波去噪分解层数的选择对去噪结果具有较大的影响。因次如何确定小波去噪的最佳分解层数对于确保驾驶性评价准确性是极为重要的。

目前，小波去噪最佳分解层数的选择方法主要可分为2种：基于信号特征的方法和基于噪声特征的方法[3]。由于在测量汽车驾驶性数据的时候存在多种不同的噪声干扰，因此基于噪声特征的方法较为复杂，与之相比，基于信号特征来选择合适的小波去噪的最佳分解层数则更为科学。而基于信号特征的选择方法，目前主要是根据信号的均方根误差、信噪比、互相关系数及平滑度来进行小波去噪参数的优化选择[4]。文献[5] 提出了通过比较信号的均方根误差变化量的大小来选择合适的分解层数；文献[6] 提出了通过将均方根误差和平滑度进行归一化，采用变异系数法将其线性组合成复合指标，从而进行分解层数的选择；文献[7] 提出通过综合考虑均方根误差、信噪比、平滑度和互相关系数来选择小波去噪的最佳分解级数。然而在实际应用过程中，虽然上述方法在分解层数选择过程中取得了一定的效果，但也都存在一些局限性：

(1)单一指标的变化规律不够准确；

(2)计算过程较为冗杂；

(3)适应性较差。

因此在上述方法的基础之上提出了一种基于熵值法的多指标融合的小波去噪分解层数的选择方法，即将均方根误差、信噪比及平滑度的变化量进行归一化之后，通过熵值法进行权值分配，将其融合成一个复合指标，从而选择最优的小波分解层数。

1 小波去噪模型及其基础评价指标

1.1 小波去噪模型

一个实际测得的信号f(i)其实是含有噪声信号的，具体可表示为以下模型

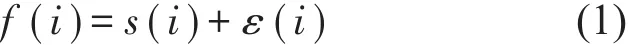
其中：f(i)为测得含噪信号，s(i)为真实信号，ε(i)为噪声信号。小波去噪过程即将实际测得的信号f(i)中的噪声信号ε(i)滤除得到真实信号s(i)的过程。主要分为以下3个步骤：

(1)通过小波对所测含噪信号进行分解。选择相应的小波基函数和分解层数N对测得的含噪信号进行N层小波分解，可获取各尺度小波系数ψji。

(2)对所得的各尺度小波系数进行阈值估计。选择合理的阈值T和相应的阈值函数对各尺度小波系数ψji进行阈值估计，从而得出各尺度小波估计系数

(3)对各尺度小波估计系数进行小波重构。根据小波分解得到的第1-N层的高频小波估计系数和第N层的低频信号系数进行小波重构，获得去噪后的信号s′(i)。

1.2 基础评价指标

小波去噪质量的基础评价指标主要有以下4种：均方根误差RMSE、信噪比SNR、相关系数R以及平滑度r。

（1）均方根误差RMSE

均方根误差指原始信号与去噪信号之间方差的平方根，其值越小，去噪效果越好。

式中：n为信号长度，f(i)为原始信号，s′(i)为小波去噪分解重构后的信号。

（2）信噪比SNR

信噪比是指信号功率与噪声功率之间的比值，其值越大，去噪效果越好。

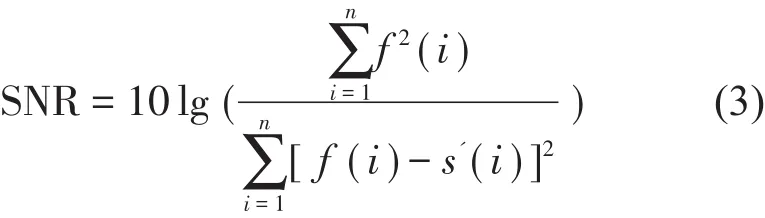
式中：n为信号长度，f(i)为原始信号，s′(i)为小波去噪分解重构后的信号。

（3）相关系数R

相关系数是指原始信号与去噪信号之间的相似度，其值越大，去噪效果越好。

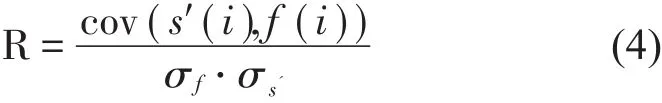
式中：σf、σs'分别为原始信号与小波去噪分解重构后的信号的标准差。

（4）平滑度r

平滑度是指去噪信号一阶差分与原始信号一阶差分之间方差根的比值，其值越小，去噪效果越好。

式中：n为信号长度，f(i)为原始信号，s′(i)为小波去噪分解重构后的信号。

2 多指标融合

上述的单一基础评价指标虽然都能在一定程度上反映去噪效果的好坏，但是都存在一定的局限性。如果能从上述基础评价指标中选取某几个从不同的方面来评价小波去噪的质量，再通过一定的方法去分配各个指标的权重，将其融合成一个复合指标，那么根据这个复合指标就能较为全面地评判去噪质量的好坏，从而进行小波去噪最佳分解层数的优化选择[8]。

2.1 基础指标的选取

选取基础指标的关键在于从多角度全面描述去噪质量的好坏。研究表明，均方根误差主要反映了去噪信号与原始信号的一个整体偏差信息；信噪比反映了噪声信号与原始信号的一个能量关系；相关系数反映了去噪信号与真实信号的一个拟合程度；平滑度反映了去噪信号与原始信号在局部程度上的逼近关系[9]。由于真实信号在实际实验过程中是未可知的，因此相关系数的参考意义不大。综上，为了全面有效地评价去噪质量，选取均方根误差、信噪比以及平滑度3个基础评价指标进行指标融合。

2.2 基础指标的改进

在理论真实信号未可知的情况下，为了更加准确进行去噪质量的评价，需要将上述基础评价指标进行改进。经研究发现，上述各选取的基础评价指标的变化量会随着分解层数的增加而表现出较为明显的收敛特性，因此借助各基础评价指标的变化量特征来进行去噪质量评价。各改进的评价指标为：

（1）均方根误差变化量Vrmse

上式中：Vrmse(m)表示第m层分解尺度下均方根误差变化量，RMSE(m+1)、RMSE(m)分别表示第m+1、m层分解尺度下的均方根误差。

（2）信噪比变化量Vsnr

上式中，Vsnr(m)表示第m层分解尺度下的信噪比变化量，SNR(m+1)、SNR(m)分别表示第m+1、m层分解尺度下的信噪比。

（3）平滑度变化量Vr

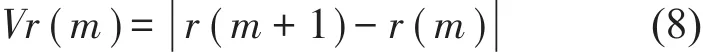
上式中：Vr(m)表示第m层分解尺度下的平滑度变化量，r(m+1)、r(m)分别表示第m+1、m层分解尺度下的平滑度。

2.3 多指标融合构建复合指标

由于上述3个改进后的评价指标物理意义不同，且基数和变化范围不同，如果仅仅将进行简单的线性组合，则组合后的结果参考意义不大，因此在进行指标融合之前，需要将其进行归一化处理[10]。即将各个指标的变化量数值规划到[0,1] 区间内，使其成为纯数值量，且其数值越小，表示去噪效果越好。归一化处理的具体形式为

上式中 ：Vrmsemax、Vrmsemin、Vsnrmax、Vsnrmin、Vrnax、Vrmin分别表示均方根误差变化量、信噪比变化量、平滑度变化量的最大值和最小值。

由于不同的评价指标所涵盖的物理意义不同，因此在进行指标融合的过程中，需要对各个评价指标进行权值分配。现通过信息熵法来确定权重。信息熵主要是从信息的不确定性和概率的角度来表征信息源的不定度[11]。在本例中，若某个评价指标给予的信息量越大，其对应的不确定性就越小，那该评价指标对应的熵值也就越小。因此可以根据信息熵的此特性，对各指标进行权重分配。根据熵值的大小判断其离散程度，离散程度越大，那么其在复合指标中影响程度越大，从而权重也就越大。本例中运用熵值法定权重的基本步骤为：

（1）选取t种小波去噪参数、m个评价指标，则xij为第i种参数的第j个评价指标的数值；

（2）指标的归一化处理（上文已进行此操作，不再赘述）；

（3）计算第j项指标下的第i种参数占该指标的比重

（4）计算第j项指标的熵值

式中：k=1∕ln(t)＞ 0；

（5）计算信息熵冗余度

（6）计算各项指标的权值

权值分配完成之后，则需要通过多指标融合构建复合指标，其具体形式为

式中：Y为融合后的复合指标，wVrmse、wVsnr、wVr分别表示由信息熵法计算得到的均方根误差变化量、信噪比变化量及平滑度变化量的权重，PVrmse、PVsnr、PVr分别表示均方根误差变化量、信噪比变化量及平滑度变化量的归一化处理的结果。

3 实例验证分析

由于在进行驾驶性试验时，受到发动机的振动、路面的不平坦、离合器的脱离接合带来的抖动等诸多因素的影响，测得的加速度信号中会有较多的噪声干扰，使得加速度信号在较短的时间内产生较大的幅值变化。现截取某品牌试验样车在驾驶性评价试验过程中所测得的部分加速度信号，如图1所示，利用上述方法进行小波去噪，从而为后续驾驶性评价提供准确的数据参考。

图1 初始加速度信号

为了更好滤除掉噪声的干扰，保留汽车驾驶性评价所需要的有用信号，选用不同的小波基函数进行对比，发现具有较高正则性和较好紧支性的sym3函数处理效果最佳。现采用小波固定阈值去噪方法，利用sym3小波基函数进行多层的信号分解与重构，其各层信号的基础评价指标如表1所示。

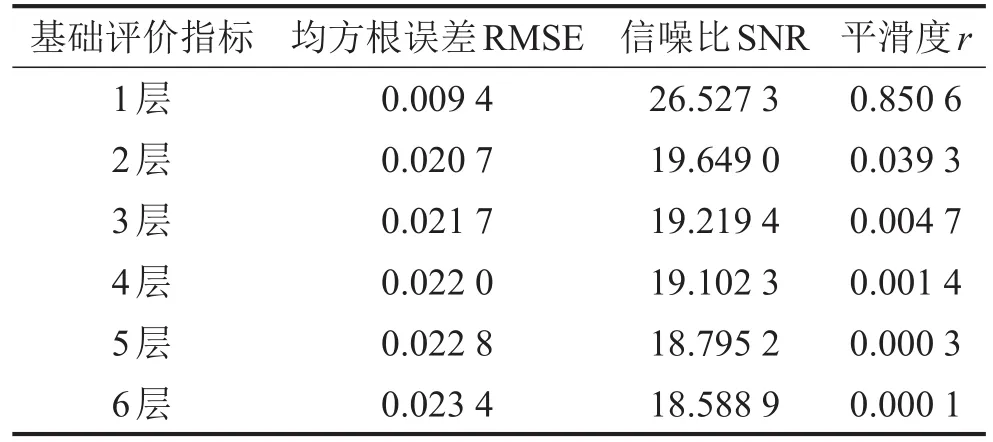
表1 各层分解的基础评价指标

再采用上述基于信息熵法的多指标融合方法进行去噪质量评价，得到如表2所示的各指标权重以及表3所示的融合后的各层复合指标Y的值。

表2 指标所占权重表

表3 复合指标数值表

由表1可知，若单纯依靠均方根误差或信噪比的基础评价指标来看，则1层分解层数去噪效果较好，若单纯从平滑度来看，则6层分解层数去噪效果较好。而在此次的小波去噪质量评价中，采用了基于信息熵的多指标融合的方法，由表2可知，此时平滑度变化量所占比重较大，这是由于平滑度体现了信号的局部细节特征，能够将汽车加速度信号的局部变化有效地保留下来。经过复合指标的计算，由表3可知，在3层分解尺度下，指标融合之后得到的复合指标Y值最小，故认为此时的去噪效果最佳。其加速度信号在1至5层分解尺度下的去噪结果如图2至图6所示。

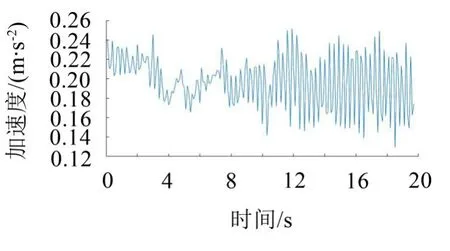
图2 分解层数为1时的加速度信号

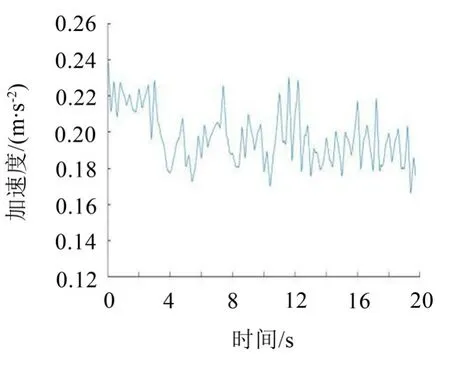
图3 分解层数为2时的加速度信号

图4 分解层数为3时的加速度信号

图5 分解层数为4时的加速度信号

从图2至图6中，可以看出分解层数为1或2时，其信号曲线振动频率依旧较大，其噪声没有滤除干净；分解层数为4或者5时，信号曲线虽然非常光滑，但是信号滤除过度，很多局部有用的振动信号也被滤除掉了；而分解层数为3时，曲线较为光滑，且有一定的小凹谷和凸起。将分解层数为3的小波去噪后的信号与原初始信号进行对比，如图7所示。

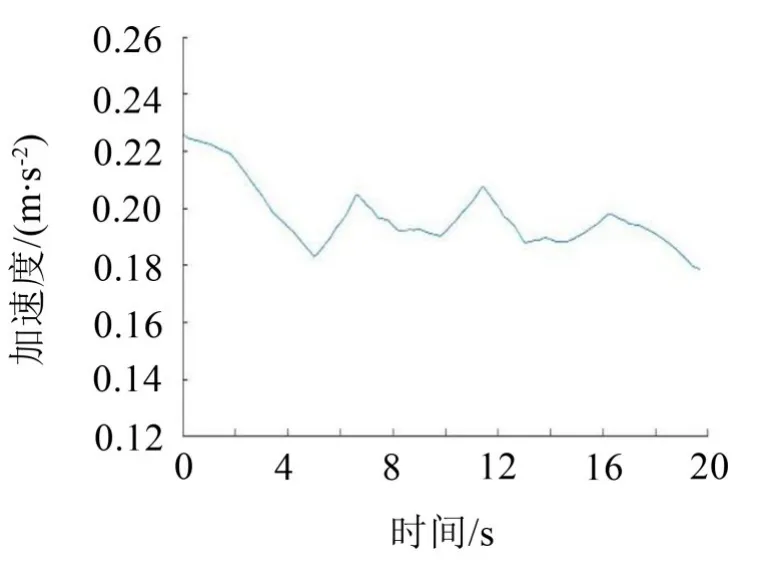
图6 分解层数为5时的加速度信

图7 初始信号及分解层数为3时的去噪后信号

采用分解层数为3的小波去噪后的信号不仅保留了原加速度信号中的整体趋势信息，而且对于局部细节信息也有较好的逼近，可以看出去噪质量较好。因此采用基础评价指标来评判去噪质量从而选择分解层数是不准确的，而采用上述基于信息熵法的多指标融合方法来确定小波去噪的分解层数则效果较好。

4 结语

针对汽车驾驶性评价过程中所采集的加速度信号，采用了基于信息熵法的多指标融合方法来确定小波去噪的最佳分解层数。首先根据4个评价指标各自的特点，选取了3个基础评价指标：均方根误差、信噪比以及平滑度；然后改进评价指标，得到其变化量；再利用信息熵法将其进行指标融合，得到复合指标，根据复合指标值的大小来选择最佳的分解层数。采用实验数据进行验证，证明了此方法简单有效，能够在滤除噪声的同时，较好地保留本身有用的整体信号和细节信息，为后续驾驶性的准确评价提供了数据保障，同时该方法具有较广的适应性，也为评价小波去噪质量提供了一种新的参考和思路。