面向OFDM系统的高精度窄带干扰抑制算法
2019-08-22胡旭东张成文刘玉涛史军王彬
胡旭东,张成文,刘玉涛,史军,王彬
(1.哈尔滨工业大学电子与信息工程学院,150000,哈尔滨; 2.通信网信息传输与分发技术重点实验室,050000,石家庄)
正交频分复用(OFDM)具有抗频率选择性衰落及高频谱利用率等特点[1],在4G系统得到了广泛的应用。但是,OFDM系统对窄带干扰(NBI)非常敏感,少量的带内NBI即可给OFDM系统带来很大的性能损失[2-4]。在军事通信领域的信息对抗中,人为的NBI会使OFDM战术电台无法正常工作;尤其是作为5G技术之一的窄带物联网(NB-IoT),对现有4G宽带系统引入了NBI[5],因此如何减轻NB-IoT对宽带系统的影响是5G发展的重要问题之一[6]。近年来,国内外学者对如何有效地抑制NBI,提高窄带干扰场景下OFDM系统的性能进行了一定的研究[7-9]。
窄带干扰抑制算法可分为时域法及频域法。时域法在接收端的FFT之前进行干扰抑制,可有效避免NBI的频谱泄漏,但存在陷波滤波器导致有效循环前缀(CP)长度减小、系统容易受到码间干扰(ISI)影响以及时域滤波器需要一定的收敛时间、设计复杂等问题[10-13]。频域法实时性高、易于实现,但如何减少NBI的频谱泄漏是其核心研究问题之一[14]。频域法的经典算法是频域置零干扰抑制法[15],但该算法会损失大量的有用信息。文献[16]在假定准确已知单音干扰频率的条件下,提出一种干扰对齐(IA)的减小NBI频谱泄漏的干扰抑制算法。文献[17]进一步提出一种结合查表法(LT)和干扰对齐(IA)的干扰抑制算法(LT-IA),但文中没有考虑干扰频率估计误差对SINR及干扰抑制性能的影响。文献[18]针对单音干扰给出一种基于FFT方式干扰频率估计的干扰抑制算法,但干扰频率估计精度较低,需要基于微调步长进行多次迭代更新。上述文献中的干扰频率估计算法误差较大且误差分布不均匀,导致经过干扰对齐后仍有较大的频谱泄漏。近年来,部分文献研究了基于压缩感知的窄带干扰抑制[19-21],但这些算法均存在抗噪性差、恢复算法复杂、干扰频率估计精度低等问题。
综上,本文针对OFDM系统的频域干扰抑制算法性能受NBI频率估计误差及频谱泄漏影响严重的问题,提出一种适于OFDM系统的高精度Chirp-Z变换(CZT)干扰频率估计结合干扰对齐(IA)的窄带干扰抑制算法(CZT-IA)。本文算法提高了NBI频率估计的精度,减小了NBI频谱泄漏,改进了OFDM系统频域置零窄带干扰抑制算法的BER性能,对于5G时代NB-IoT窄带网络与OFDM系统的共存与兼容、提高OFDM系统对环境的普适性具有一定的理论及应用价值。
1 窄带干扰模型及频谱泄漏
窄带干扰可建模为单音干扰[2,16],时域单音干扰可表示为
i(t)=A0exp[j(2πfit+θ0)]
(1)
式中:A0、fi、θ0分别为单音干扰的幅度、频率和相位。
OFDM子载波间隔及子载波频率分别为
(2)
式中:fs是采样频率;N是FFT点数;n是子载波标号,0≤n≤N-1。
单音干扰的频率fi可表示为
fi=(m+a)Δf, 0≤m≤N-1,|a|≤0.5
(3)
式中:m为整数因子;a为分数因子,表征了单音干扰相对OFDM子载波m的频率偏移;Δfi为单音干扰的频率偏移,可表示为
Δfi=aΔf, |a|≤0.5
(4)
接收端一个OFDM符号周期的NBI时域抽样可表示为
i(n)=A0exp[j(2πfints+θ0)]=
n=0,…,N-1
(5)
对i(n)进行FFT变换后,第k个子载波位置的频域干扰可表示为
k=0,…,N-1
(6)
由式(6)可得
(7)
当a=0时,有
(8)
当a≠0时,有
|I(k)|=
(9)
以信干比为-15 dB、干扰频率整数因子m=100的单音干扰为例,不同分数因子a对应的单音干扰频谱泄漏如图1所示。
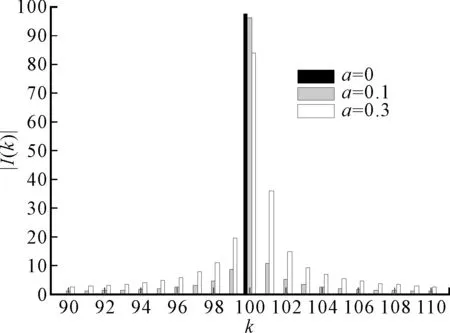
图1 不同分数因子a对应的单音干扰频谱泄漏
由图1可见:当a=0时,单音干扰的能量集中在子载波m上,单音干扰对其他子载波没有频谱泄漏;然而,随着a的增加,单音干扰对邻近多个子载波的频谱泄漏越来越严重。这正是由于分数因子的存在,使得单音干扰与OFDM子载波不正交,导致干扰信号频谱泄漏的结果。
分析图1并结合|I(k)|的对称性可得,存在某个分数因子门限值ath,使得当|a|≤ath时,在频域仅置零子载波m就可以消除大部分干扰能量。为了推导该门限值,首先定义一个表征频谱泄漏程度的参数——干扰能量集中率R=|I(m)|2/Ei,其中|I(m)|2表示第m个子载波上的干扰能量,Ei表示干扰总能量。R越大,干扰能量越集中,表示频谱泄漏越少。由式(9)可得
(10)
(11)
式(11)中第2个等号用到了帕萨瓦尔定理。
由式(10)(11)可得
(12)
取N=512,当|a|=0.005时,R=0.999 9,即在频域将第m个子载波的数据置0,就可以抑制99.99%的干扰能量。故可得出结论:取ath=0.005,当|a|≤ath时,频域置零法可以实现有效的干扰抑制。
干扰能量集中率R与干扰频率分数因子a的关系如图2所示。
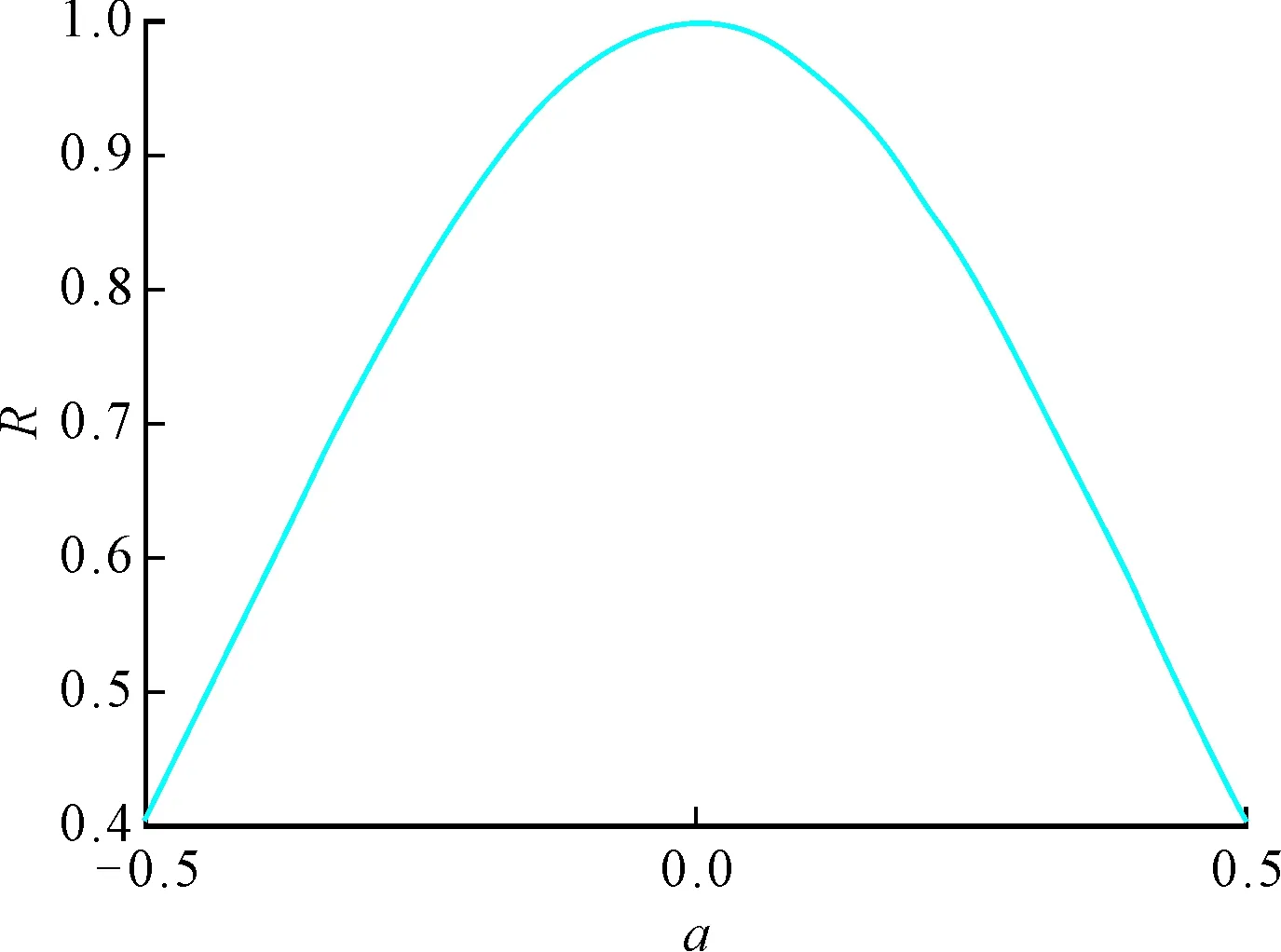
图2 干扰能量集中率R与干扰频率分数因子a的关系图
由图2可见,|a|越大,集中率R越小,表明干扰能量越分散,受NBI频谱泄漏影响的子载波越多,传统频域置零法就会把受干扰的子载波置零,这将恶化系统误码性能。因此,频域置零法要想取得较好的性能,必须采取有效的方法,以减小a导致的频谱泄漏。
2 干扰对齐的频域置零干扰抑制算法
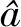
(13)
i′(n)经过FFT后,频域的干扰可以表示为
(14)
式中:k=0,…,N-1。由式(14)可得
(15)
当ε→0时,由式(15)可得
(16)
由式(13)(16)可见,只要分数因子估计误差ε足够小,经式(13)变换后的单音干扰的频域能量可近似集中在第m号频点上,而在其他频点几乎不存在频谱泄漏,定义该过程为干扰对齐。干扰对齐的作用是减少由于分数因子a导致的干扰信号的频谱泄漏。
通过以上分析,基于干扰对齐的窄带干扰抑制算法的原理如图3所示。
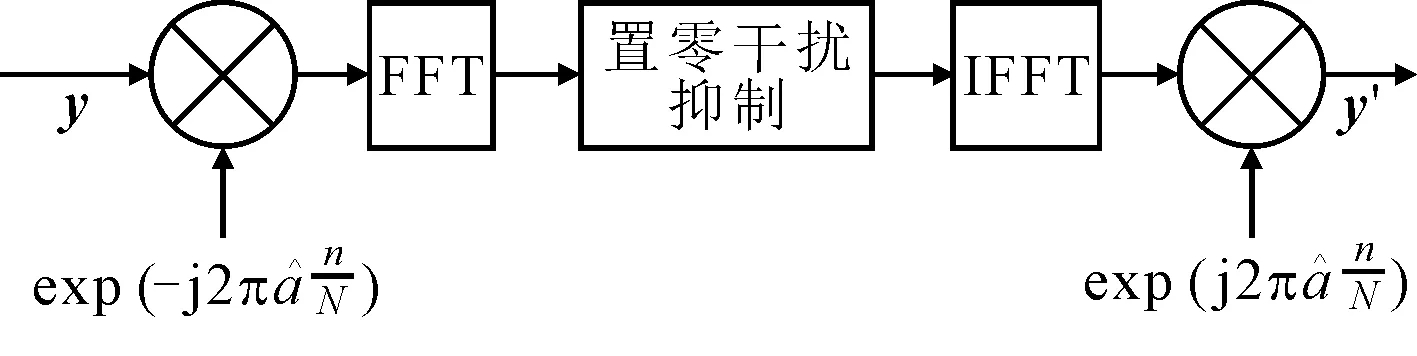
图3 基于干扰对齐的窄带干扰抑制算法原理
移除循环前缀后,时域接收信号y表示为
y=x+i+w
(17)
式中:y=[y(0),…,y(N-1)]T是长度为N的接收信号的时域抽样;x=[x(0),…,x(N-1)]T是长度为N的发射信号,E[xxH]=EsIN;i=[i(0),…,i(N-1)]T是单音干扰,i(n)如式(5)所示;w=[w(0),…,w(N-1)]T是加性高斯白噪声,E[wwH]=σ2IN。
经过基于干扰对齐的窄带干扰抑制算法处理后,时域接收信号y′表示为
(18)
式中:F、FH分别代表FFT、IFFT变换矩阵;IN是N阶单位阵;em是单位阵的第m列;对角矩阵D、DH是频率搬移、逆搬移矩阵
D=
(19)
3 FFT与CZT结合的干扰频率估计
CZT能够在不增加采样点数的情况下,在所选频带内获得任意大小的频率分辨率,是频谱细化的一种重要方法。结合OFDM系统的特点,本节给出一种适于OFDM系统的FFT与CZT结合的高精度窄带干扰频率估计算法。算法步骤如下。
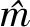
(2)利用CZT变换估计单音干扰的频率。对式(17)中的OFDM接收信号在m′-1和m′+1两个子载波间的频段进行M点的CZT,得到该频段的细化频谱,CZT变换如下
(20)
式中:A=A1exp(jθ1)=A1exp(j2πf1/fs),θ1表示起始采样点对应的相角,f1为对应的起始频率,取f1=(m′-1)Δf,A1表示起始采样点对应的半径,取A1=1;W=WΔexp(-jφΔ)=WΔexp(-j2πfΔ/fs),WΔ称为采样线的伸展率,取WΔ=1,φΔ为采样点的角频率间隔,fΔ为采样点的频率间隔,取fΔ=2Δf/M,此时,CZT的频率分辨率为ΔfCZT=fΔ=2Δf/M。
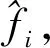
(21)
证明根据式(20),式(5)中i(n)的M点CZT可表示为
(22)
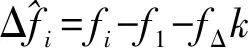
|ICZT(k)|=
(23)
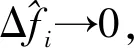
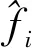

(24)
比较式(21)及(24)可得,干扰频率的整数因子及分数因子的估计值可由式(25)求得

(25)
(26)
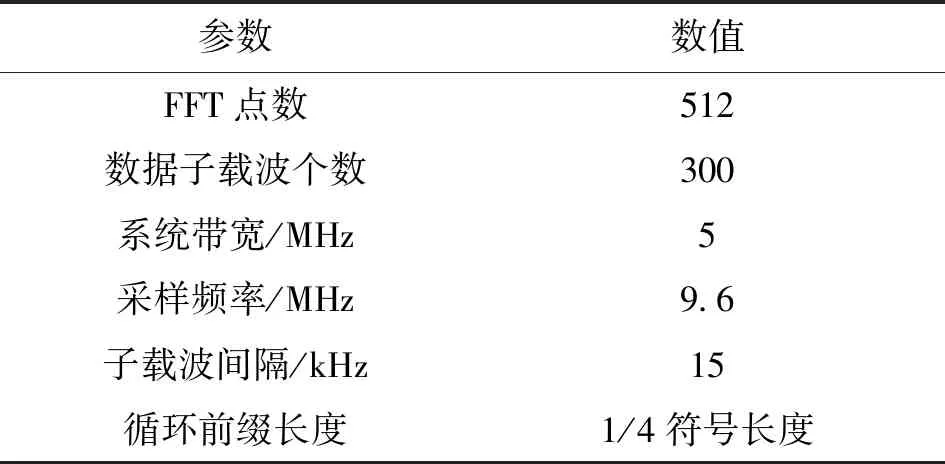
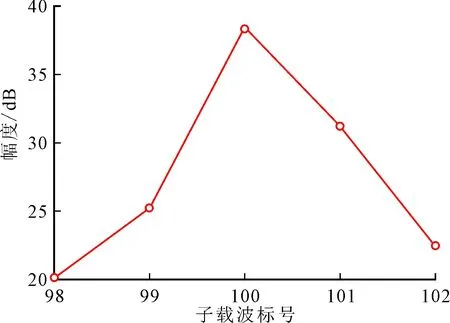
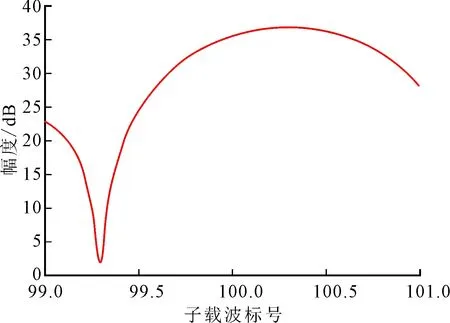
由式(26)可得,当M=N=512时,有|ε|≤0.002 考虑干扰频率估计误差及基于干扰对齐的干扰抑制算法中频域置零过程对有用信号和噪声的影响,对所提CZT-IA干扰抑制算法的信干噪比分析如下。 由式(18)可得 y′=(IN-ggH)y=(IN-ggH)(x+i+w)= x′+i′+w′ (28) 式中:g=DHFHem;x′=(IN-ggH)x;i′=(IN-ggH)i;w′=(IN-ggH)w。 由于有用信号和噪声的能量在频域是近似恒定的,干扰对齐后的能量分别为 (N-1)Es (29) (N-1)σ2 (30) 由于NBI的能量在频域比较集中,因此不能应用上述方法进行推导,对其推导如下。 由式(15)可得,干扰对齐后在频点m上的NBI能量为 (31) 式(11)给出干扰抑制前的干扰总能量为 因此,可以推得干扰置零后残留的NBI能量为 (32) 所以,频域置零前的信干噪比RSIN为 (33) (34) 定义信干噪比增益为 (35) 由上述公式可见,干扰频率估计越准确,即ε越小,则G越大、干扰抑制越充分。 在MATLAB环境下搭建了OFDM系统,其中信道采用高斯白噪声信道,信道编码采用Turbo码(码率为1/3),调制方式采用QPSK调制,仿真中相关参数配置如表1所示。 表1 仿真参数配置 (a)FFT后的频谱 (b)CZT细化后频谱图4 接收信号FFT后频谱及CZT细化后频谱比较 为了比较CZT的频率估计精度,图4给出m=100、a=0.3、A0=4.3时接收信号FFT后的干扰频率附近频谱以及经过CZT细化后的频谱。由图4可见,相比直接FFT得到的频谱,经过CZT细化后的频谱峰值更接近实际干扰频率,基于CZT的干扰频率估计具有更高的精度。 为了比较不同分数因子a对系统性能的影响,图5给出频域置零法与已知a的理想干扰对齐法(I-IA)的误比特率曲线。由图5可见,频域置零法仅在a=0.005时性能与I-IA接近,且随着a的增大,系统的误比特率性能迅速下降,这是因为随着a的增大频谱泄漏严重,频域置零法需要置零多个子载波才能达到有效的干扰抑制,该过程损失了大量有用信息,从而导致误比特率性能下降。I-IA算法的性能不随分数因子的改变而改变,且随着SNR的增加,系统的误比特率性能均得到改进,这正是由于干扰对齐法减小了因分数因子a导致的频谱泄漏的结果。 图5 频域置零法与I-IA法的误比特率对比 为了比较NBI的频率估计误差及其对系统性能的影响,图6给出文献[17]采用的LT-IA算法、基于本文CZT干扰频率估计及文献[13]IIR陷波滤波器的干扰消除算法(CZT-IIR)及本文提出的CZT-IA算法在不同分数因子a时的误比特率性能。由图6可见:LT-IA算法在a=0.3时的性能明显优于a=0.1及a=0.5时的性能,这正是由于查表法在|a|→0及|a|→0.5时,干扰频率估计误差受信号和噪声功率的影响较大所致,导致干扰频率估计误差分布不均匀;本文所提CZT-IA算法与CZT-IIR算法在不同a时误比特率性能十分接近,都具有较理想的干扰抑制效果,且与图5中理想干扰对齐法的误比特率性能接近,这正是由于所提算法对a的估计具有较高的精度且估计误差分布均匀的结果;相比CZT-IIR算法,本文所提CZT-IA算法具有更好的实时性及更低的复杂度。综上,本文所提CZT-IA算法对a的估计具有较高的准确度和稳定性,能够减小窄带干扰的频谱泄漏,提高受窄带干扰影响的OFDM系统的误比特率性能。 图6 LT-IA算法、CZT-IIR算法及CZT-IA算法的误比特率对比 本文分析了单音干扰频率、频率估计误差与干扰频谱泄漏、信干噪比的定量关系及其对OFDM系统误比特率性能的影响,提出一种高精度的FFT与CZT结合的干扰频率估计及干扰对齐的频域窄带干扰抑制算法。实验结果表明:本文算法有效减小了干扰信号频谱泄漏,同时较理想地抑制了窄带干扰,提高了存在窄带干扰时OFDM系统的误比特率性能。4 信干噪比分析
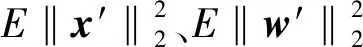
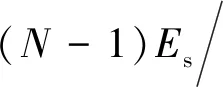
5 仿真结果


6 结束语
