精细谱负熵及其在滚动轴承故障诊断中的应用
2019-08-22胥永刚田伟康曹金鑫马朝永
胥永刚,田伟康,曹金鑫,马朝永
(北京工业大学机电学院智能监控与诊断研究所,100124,北京)
滚动轴承广泛应用于各种机械设备中,轴承的健康状况影响着机械设备的工作性能,因此对滚动轴承的故障进行诊断具有重要意义。振动信号包含着丰富的设备状态信息[1-2],但由于工作环境的复杂性,轴承故障特征常淹没在噪声中,共振频带不明显,给故障特征的提取带来了很大的困难。峭度指标对冲击性成分十分敏感[3],能检测信号中的突变成分,常用于轴承故障诊断中。Antoni将基于短时傅里叶变换的谱峭度引入机械故障诊断领域[4],并提出快速谱峭度图(FK)[5],用于确定共振频带的中心频率与带宽,实现了故障特征成分的提取。随后,众多学者将FK与其他方法有机结合,用于机械设备的故障诊断中[6-9]。针对谱峭度易受噪声干扰的问题,王冬等提出一种基于稀疏值的故障特征检测方法Sparsogram[10],并结合遗传算法应用到轴承故障诊断中[11]。Moshrefzadeh等提出Autogram方法,对信号平方包络的自相关求峭度,通过筛选最大值的方法来提取周期性冲击分量并进行故障诊断[12]。以上方法都没有突破FK方法频带划分的局限性,不能得到精确的频带宽度和中心频率,导致提取出的分量信噪比较低。Barszcz等提出基于窄带包络谱幅值的Protrugram方法进行故障特征频率的提取[13],效果优于FK方法,但带宽需要反复预设才能得到理想的效果[14]。Antoni提出Infogram方法并引入谱负熵的概念,同时考虑信号的冲击性和循环平稳性,以取得更为理想的故障特征分量[15],在机电设备故障诊断中得到应用[14,16],但仍存在确定的中心频率和带宽不合理的问题。
为了选取更优频带,确定最合适的中心频率和带宽,同时降低噪声对特征提取的影响,本文提出一种基于经验小波变换的精细谱负熵(ASNE)方法。利用经验小波滤波器[17],对信号频带进行变带宽扫描滤波,并对扫描得到的滤波分量进行谱负熵计算,提取最大谱负熵对应的频段进行包络谱分析,实现轴承的故障诊断。变带宽扫描滤波突破了FK和Infogram方法频带划分固定的局限性;谱负熵方法能够检测故障信号中的周期性特征和冲击性特征,提高了抗干扰能力。
1 谱负熵原理
Antoni认为振动信号中冲击成份的出现可视为系统偏离了平衡状态,在时域中表现为局部能量的波动,其对应的平方包络(SE)谱熵降低[15];如果能量的波动呈现周期性变化(即周期性冲击),反映在包络谱上,可以认为频域中出现了局部能量的波动(在某一频率处出现较大峰值),因此对应的平方包络谱(SES)的谱熵值也随之降低。
SE谱熵与SES谱熵的表达式分别为
Hε(f;Δf)=
(1)
HE(f;Δf)=
(2)
式中:〈·〉为均值计算;εx(n;f,Δf)为一个离散信号x(n)(n=0,…,L)在频率[f-Δf/2,f+Δf/2]范围内的平方包络,其表达式如下
εx(n;f,Δf)=|x(n;f,Δf)|2
(3)
Ex(α;f,Δf)为离散信号x(n)(n=0,…,L)在频率[f-Δf/2,f+Δf/2]范围内的平方包络谱,其表达式[15]如下
(4)
峭度是检测信号冲击性的指标,当出现冲击成分时,峭度值变大,这与谱熵恰巧相反。为了使二者变化规律一致,Antoni定义了谱负熵(谱熵的负值)。时域中信号平方包络的谱负熵ΔIε和频域中平方包络谱的谱负熵ΔIE分别为
ΔIε=-Hε=
(5)
ΔIE=-HE=
(6)
在轴承正常运转时,系统处于稳定状态,振动信号的谱熵最大,对应的ΔIε与ΔIE最小;当轴承出现故障时,时域波形中出现周期性冲击,谱熵值变小,对应的ΔIε与ΔIE随之变大,而对于随机性冲击,在信号的平方包络(SE)中可以体现出来,但在平方包络谱中则不易发现。因此,ΔIε与ΔIE能检测周期性冲击,同时,ΔIε也能检测到随机冲击。与时域的谱峭度相比,频域中的谱峭度更适用于窄带调制信号的提取[18],因此ΔIE也存在这样的问题。在轴承故障诊断中,确定的工作边频带过窄,则会丢失一部分有用信息,影响对轴承故障的诊断。
进一步研究发现,求信号本身的谱负熵更利于获得合适的带宽,从而提取更为丰富的故障信息。定义信号本身的谱负熵为
(7)
ΔIx越大,信号中包含的周期性冲击越明显,故本文选取ΔIx作为特征分量的筛选指标。
2 改进经验小波变换
2.1 经验小波变换原理
Gilles针对EMD方法的不足,结合小波变换,提出了经验小波变换[17],该方法广泛应用于旋转机械的故障诊断中[19]。该方法基于Little-wood Paley和Meyer小波变换,根据傅里叶信号频谱特性进行自适应划分,建立一个滤波器组以提取不同的AM-FM成分。假设用傅里叶紧支撑将[0,π]分割成N个连续部分Λn,定义ωn为各个连续部分的边界,如图1所示。以ωn为中心,根据Meyer小波变换确定经验小波尺度函数和小波函数,并构造经验小波滤波器如下
(8)
(9)
式中:β(x)为在[0,1]区间满足K阶导任意函数。τn与β(x)表示如下
(10)
根据经典小波变换的构造方法,信号f(t)的经验小波变换细节系数和近似系数的计算方法为
(11)
(12)
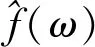
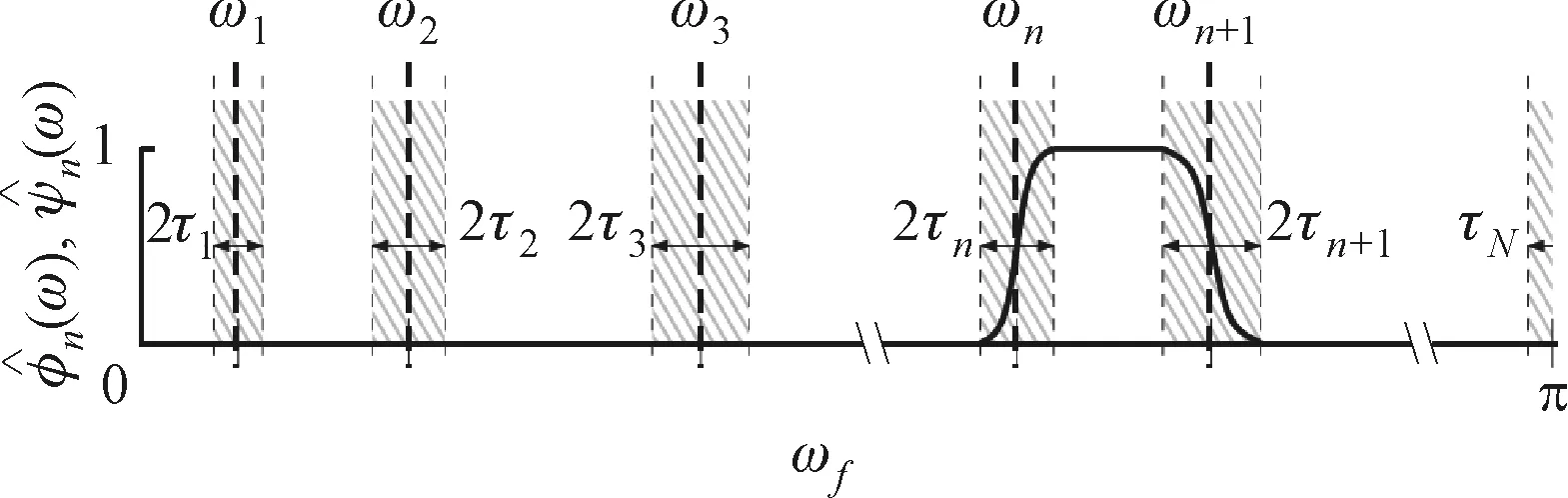
图1 傅里叶轴的划分
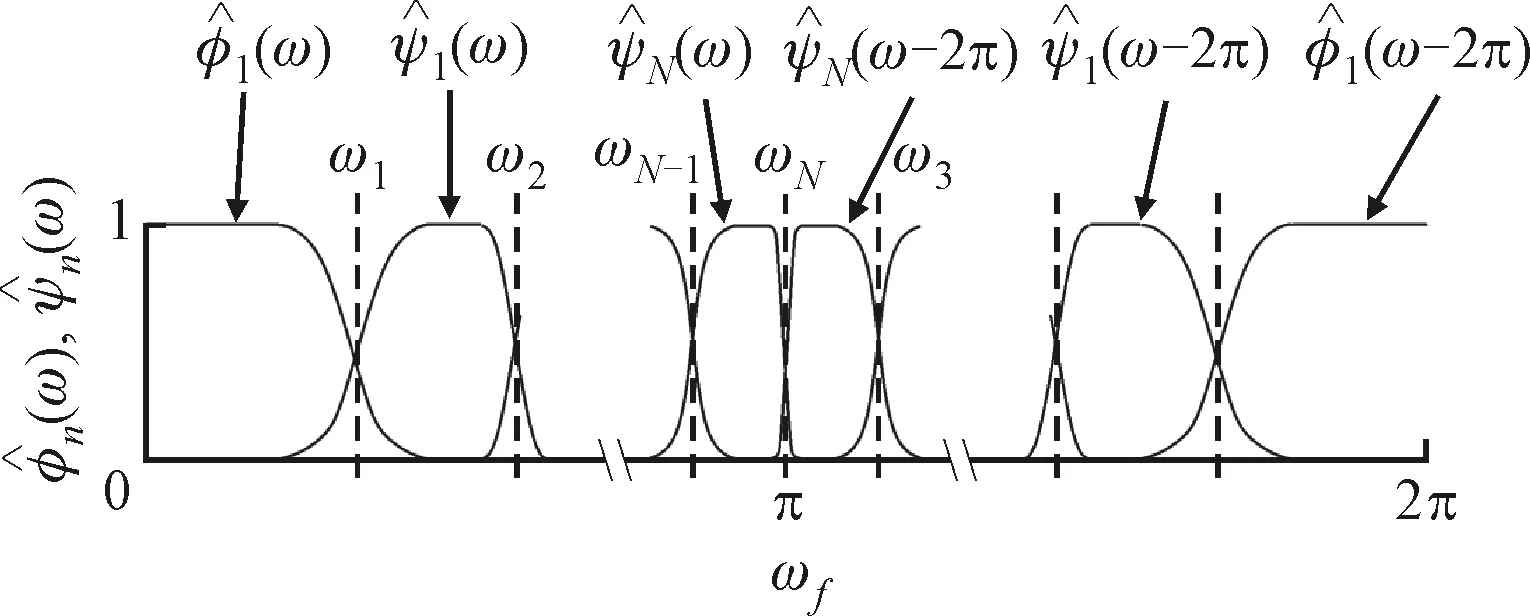
图2 经典小波滤波器组对频谱的分割
由以上公式可得到经验小波变换对应的分量
(13)
(14)
2.2 频带边界的划分
频带边界划分是经验小波变换中的关键问题,Gilles在文献[17]中给出了多种频带划分方法,实现了经验小波变换对信号频带的自适应划分。对于轴承振动信号,EWT存在频带划分不合理的问题[20]。对EWT频带划分方法进行改进,利用其紧支撑特性和能量泄露少的特点,构造多个带通滤波器对轴承振动信号进行有规律的滤波处理,并对得到的滤波分量进行筛选,获得最适中心频率和带宽,以得到最优共振边频带。
改进的EWT频带划分方法如下。在[0,π]上用ωfi-ωBj和ωfi+ωBj对整个归一化的傅里叶谱进行划分,并以边界ωfi-ωBj、ωfi+ωBj构造经验小波滤波器,对傅里叶范围为[ωfi-ωBj,ωfi+ωBj]区间进行滤波处理。ωfi为中心频率,图3给出了频带划分的规律变化,其中ωfi+1=ωfi+1+Δωf。该滤波器实现了对信号从低频至高频的扫描滤波,以获得最适合中心频率。滤波器在傅里叶频谱中的带宽为2ωBj,设定2ωBj按Δωb由小到大递进变化,以获得最优带宽,如图4所示。
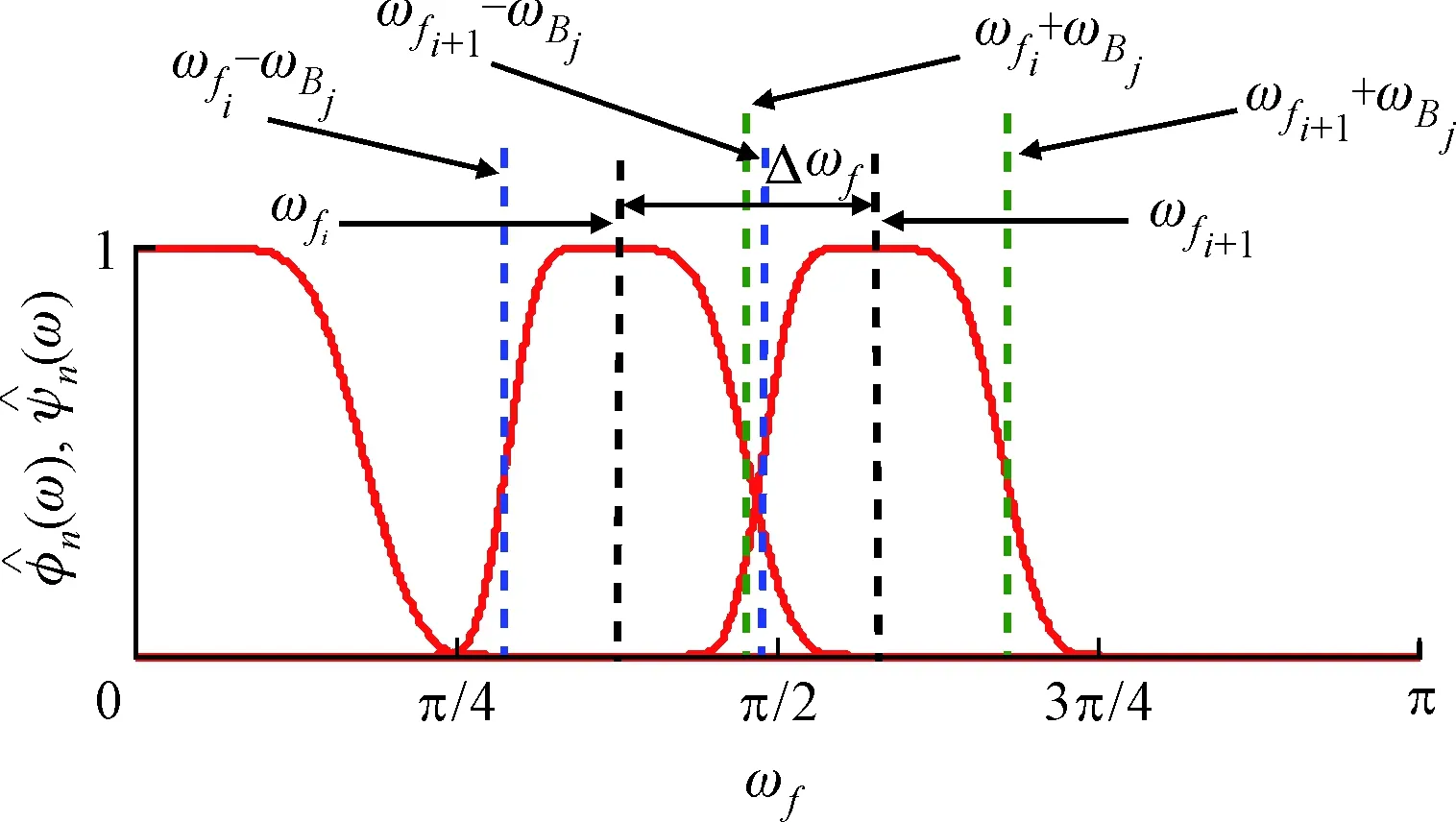
图3 频带划分的规律变化
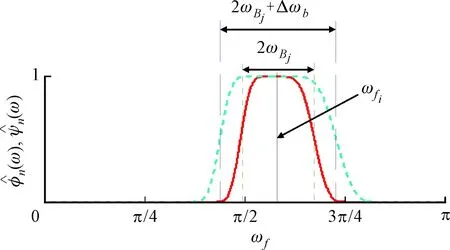
图4 滤波器的带宽变化
3 精细谱负熵方法
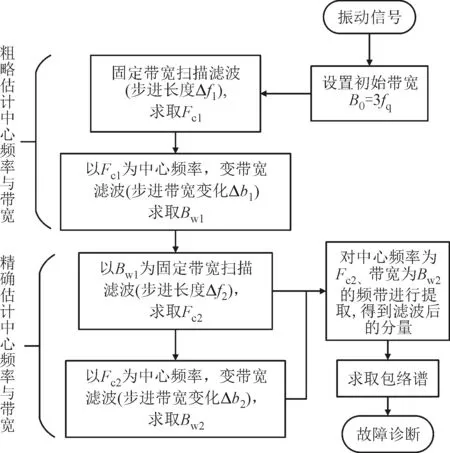
图5 精细谱负熵方法流程图
为了更好地提取出周期性冲击的成分,本文采用改进的经验小波变换对信号进行不同带宽的扫描滤波,提取出一系列不同频带的模态分量,然后对这些分量求取时域信号的谱负熵ΔIx,并对ΔIx进行极值筛选。谱负熵越大,说明该频率范围内包含的周期性冲击信息越多。提取最大谱负熵对应的模态分量,并对其进行Hilbert变换求取包络谱,能够实现对轴承的故障诊断。图5给出了精细谱负熵方法的流程图,图6给出了精细谱负熵方法的两种扫描滤波过程,图6a为固定带宽进行扫描滤波,通过筛选最大谱负熵可以得到最合适的中心频率。图6b为选定最合适的中心频率后,变化带宽滤波,通过筛选最大谱负熵可以得到最优带宽。
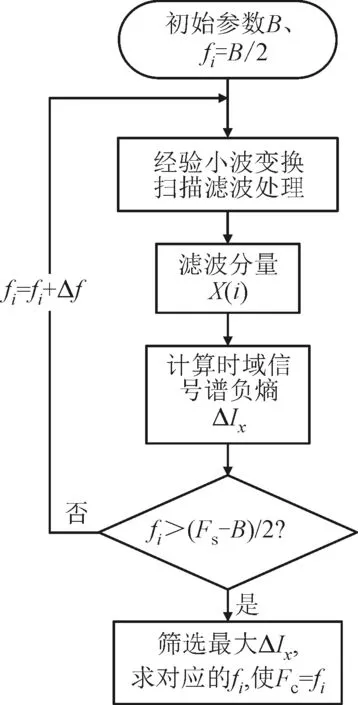
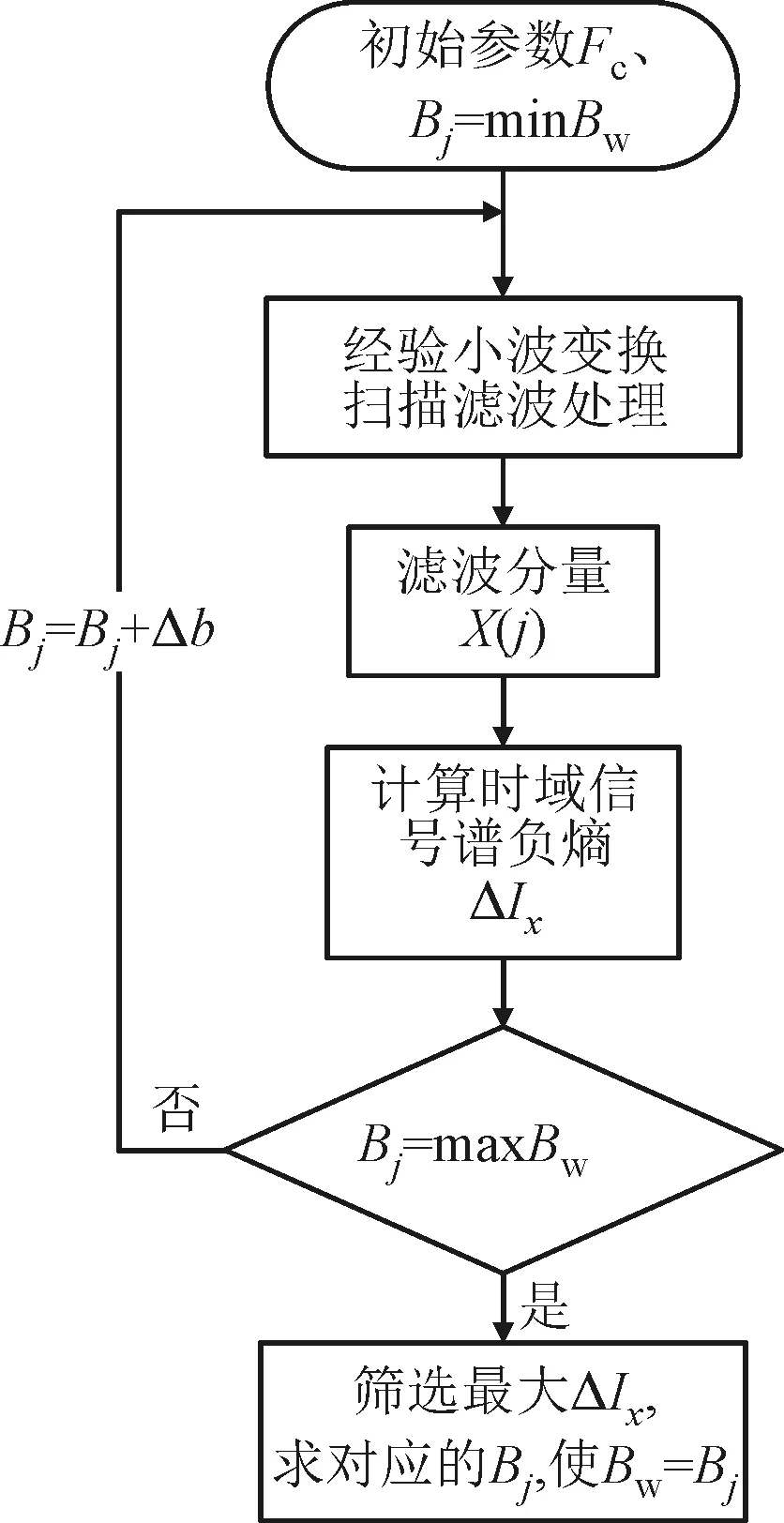
(a)固定带宽扫描滤波 (b)中心频率固定变化带宽滤波
图6 精细谱负熵方法的两种扫描滤波过程
本文提出的精细谱负熵方法步骤如下。
步骤1粗略估计中心频率和带宽。首先确定初始滤波器带宽B0,文献[14]提出带宽为3~5倍的特征频率较为合理,这里取B0=3fq(fq为故障特征频率)。首先带宽固定,中心频率以Δf1为步长进行扫描滤波,求出谱负熵ΔIx曲线,得到最大ΔIx对应的中心频率Fc1,然后以Fc1为固定中心频率,Δb1为带宽变化量对信号进行滤波处理,得到估计带宽Bw1,实现对中心频率和带宽的粗略估计,这个过程称为第1次扫描循环。
步骤2精确估计中心频率和带宽。带宽和中心频率的变化都会影响ΔIx的大小,因此想找到最优带宽和中心频率需要进行多次扫描处理,而过多的扫描循环会增加计算时间,降低该方法的运行效率。经验证,两次扫描循环后得到的带宽和中心频率即可达到最优。第2次扫描循环中,中心频率的变化量Δf2=Δf1/10,带宽变化量Δb2=Δb1/10,第2次扫描循环的变化率可根据情况自行设置,带宽和中心频率分别为Bw2、Fc2,此频带可视为最优共振频带。
步骤3故障特征频率的提取。以Fc2为中心频率,Bw2为带宽对信号进行滤波处理,提取故障特征分量。进一步做包络谱分析,实现轴承故障的诊断。
4 故障轴承仿真信号验证
构造一组轴承外圈故障仿真信号,中心频率为2 700 Hz,故障特征频率fq为100 Hz,仿真公式如下
(15)
式中:n(t)为噪声信号;x(t)为脉冲函数;n、T0分别为脉冲个数和脉冲周期;p(t)为调幅信号,其中心频率为fk。
图7给出了轴承外圈故障仿真信号及其频谱。采样频率Fs=10 kHz,采样点数N=104。由图7可见,共振边频带的理想带宽Bw约为700 Hz,提取该频段范围内的分量得到的故障特征信息最为丰富且包含噪声较少。
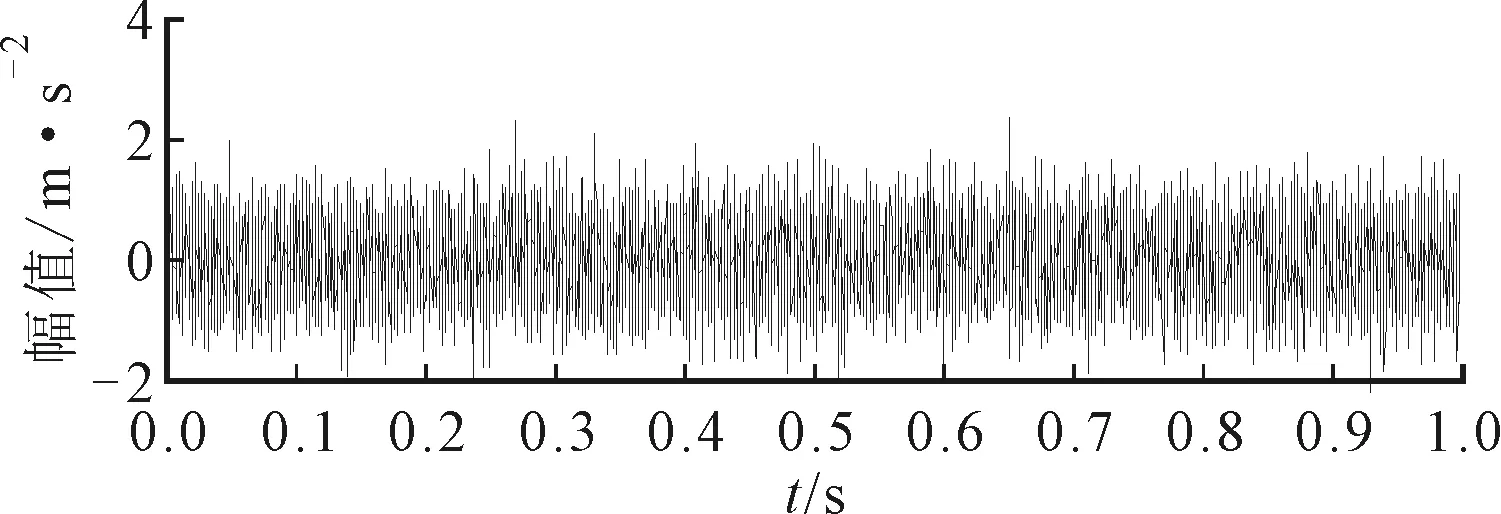
(a)波形
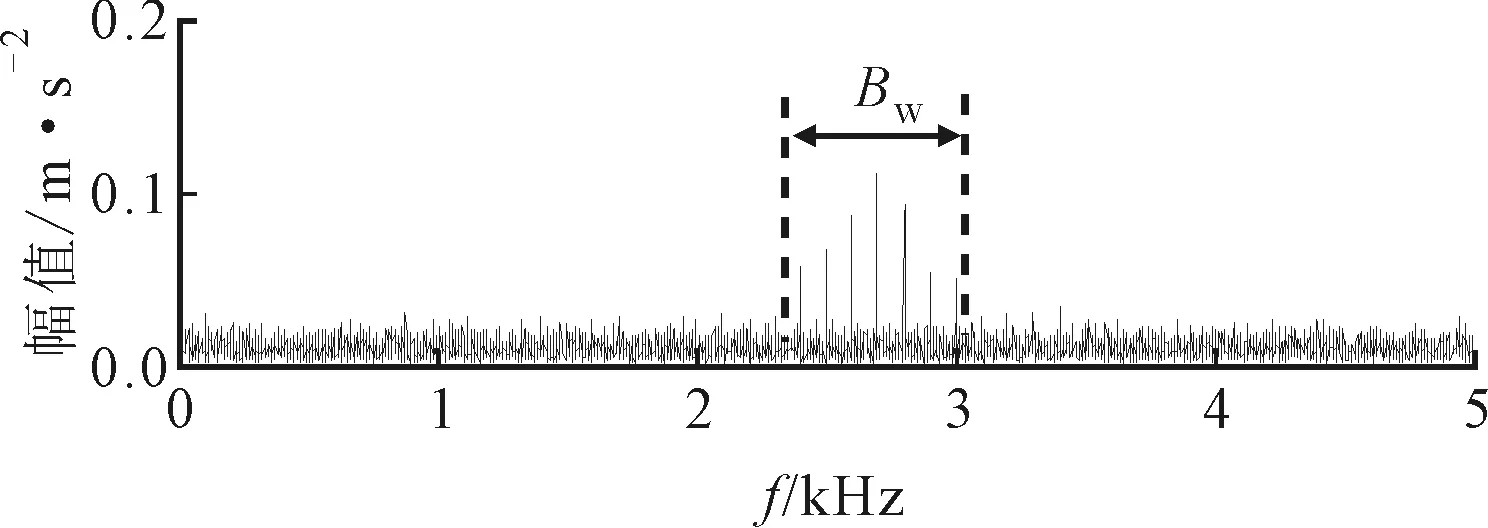
(b)频谱图7 轴承外圈故障仿真信号及其频谱
初始带宽设为300 Hz(3fq),Δb1与Δf1均设为50 Hz。图8为第2次循环扫描后得到的扫描谱负熵曲线,由图8可知,经过ASNE方法确定的中心频率Fc2=2.695 kHz,带宽Bw2=0.63 kHz。图9为提取的对应频段分量。由图9可以看出,提取分量的时域波形中,周期性冲击特征明显;频谱中得到的共振边频带频率范围与理论范围基本一致;其包络谱中出现了明显的故障特征频率及其倍频成分。
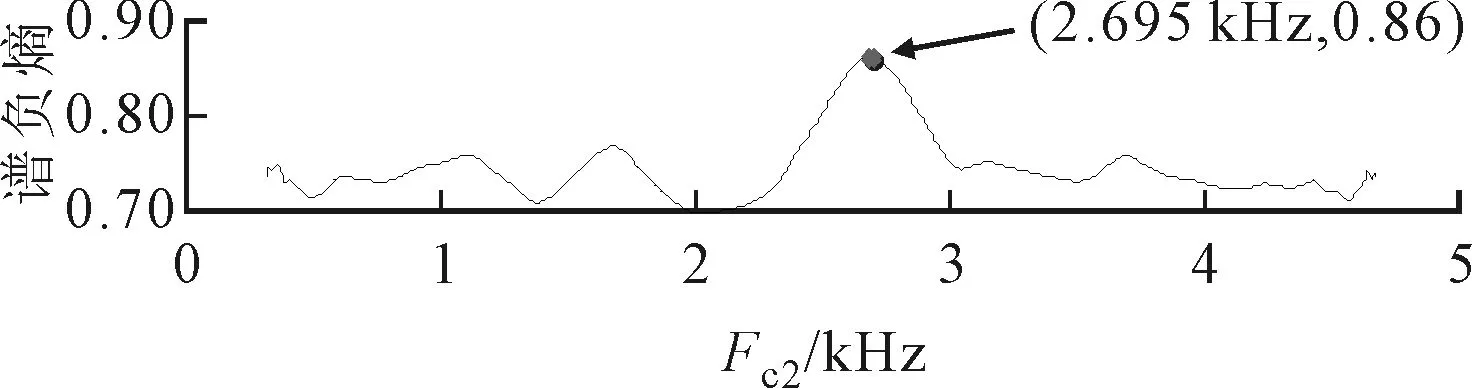
(a)固定带宽
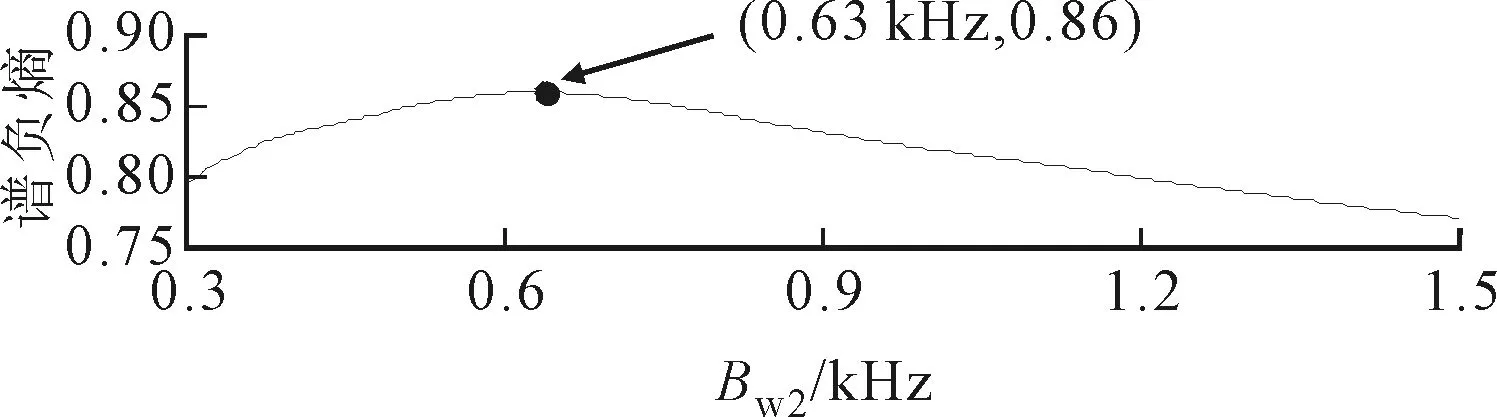
(b)固定中心频率图8 ASNE方法的中心频率与带宽的扫描谱负熵曲线

(a)波形
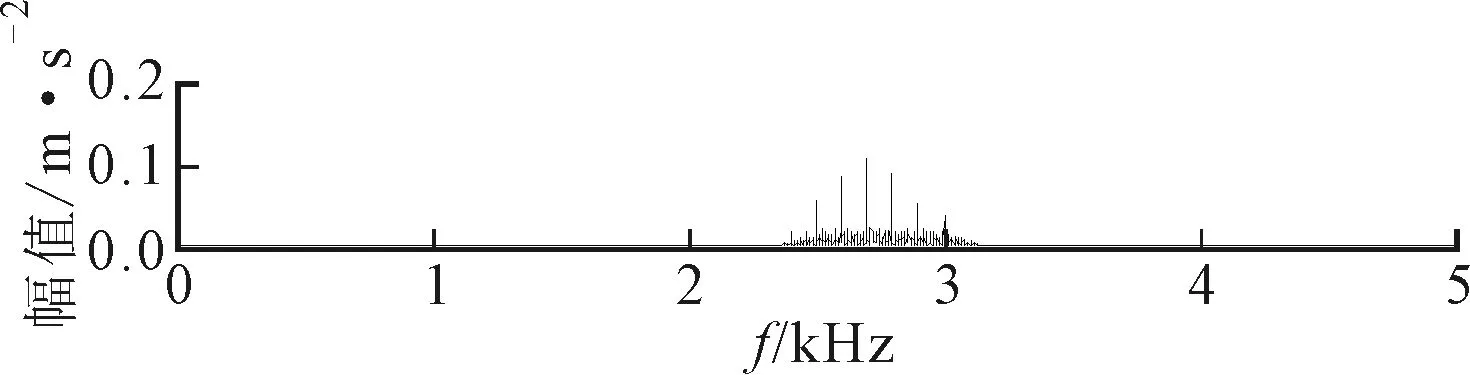
(b)频谱
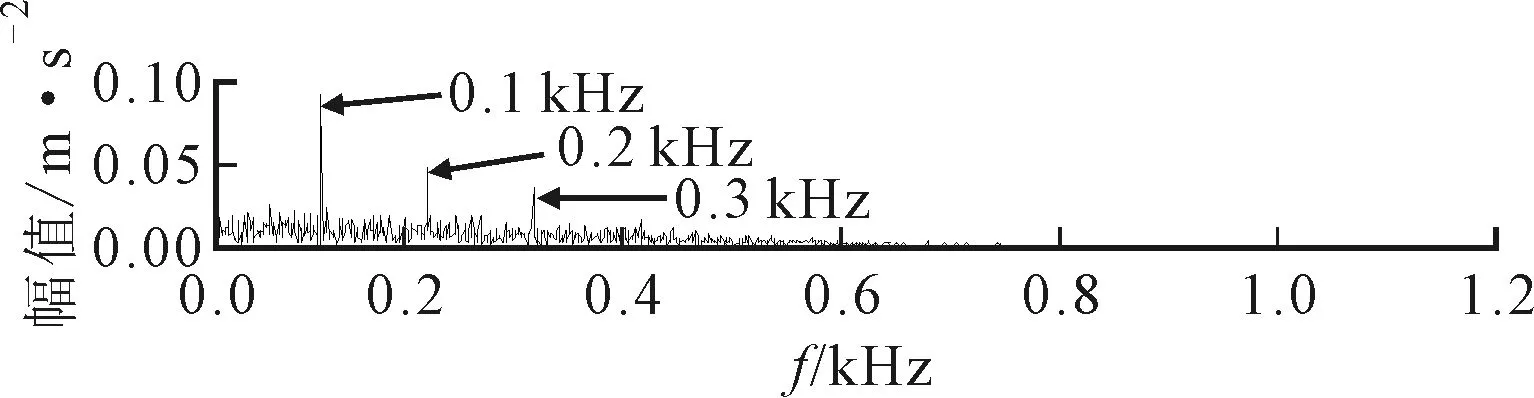
(c)包络谱图9 仿真信号故障特征提取分量
Infogram方法采用信号的SE进行谱负熵计算,但是以SE的谱负熵作为精细谱负熵的筛选指标却得不到理想效果。图10为SE的谱负熵中心频率与带宽的扫描曲线,通过寻找最大谱负熵,最终确定的中心频率为0.25 kHz,带宽为0.30 kHz,这与理想的共振边频带范围完全不符。在噪声干扰下,信号时域的谱负熵ΔIx比SE的谱负熵ΔIε更容易检测出周期性冲击成分。仿真结果表明,ΔIx能够有效地提取出振动信号中更丰富的故障特征成分。
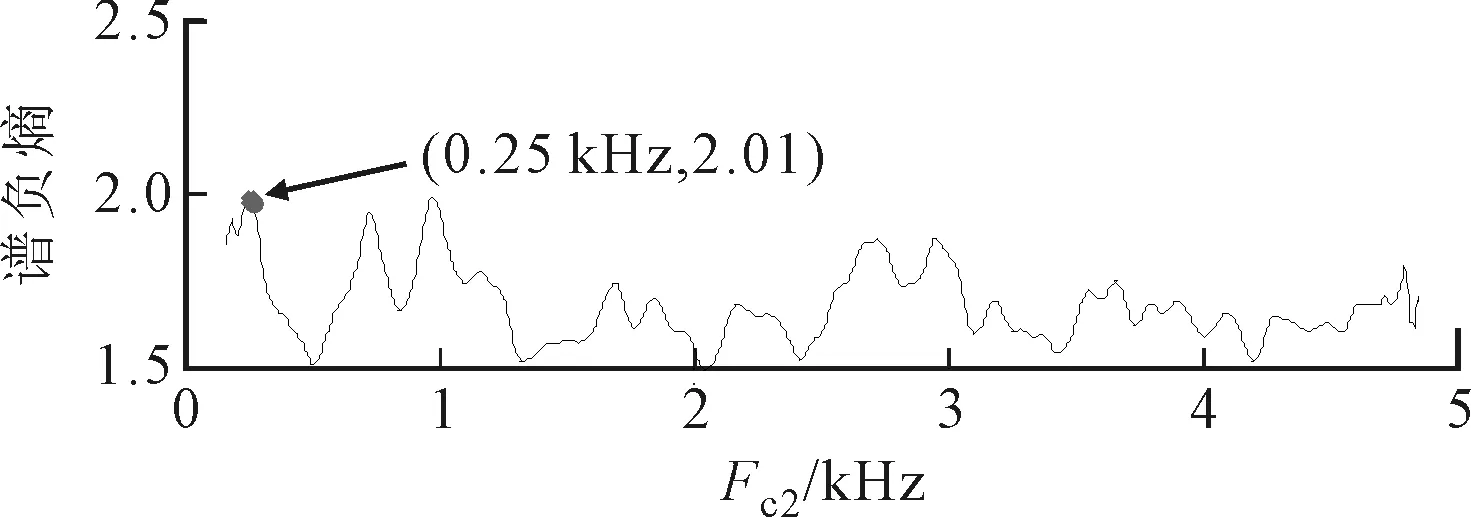
(a)固定带宽
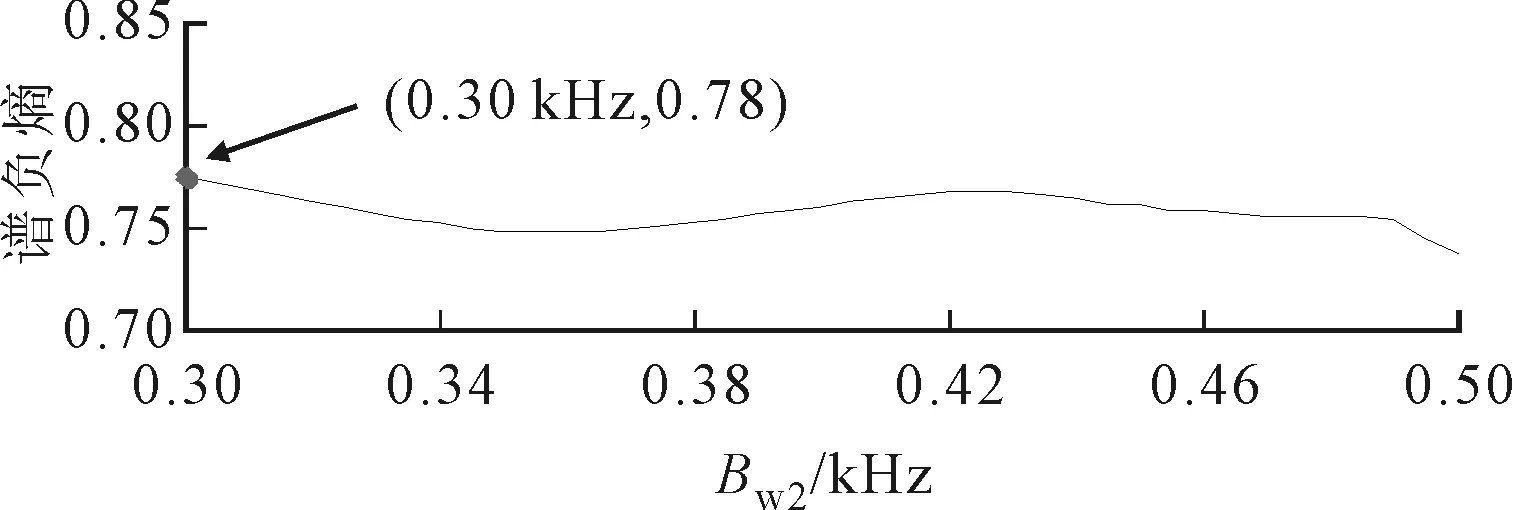
(b)固定中心频率图10 SE的中心频率与带宽的扫描谱负熵曲线
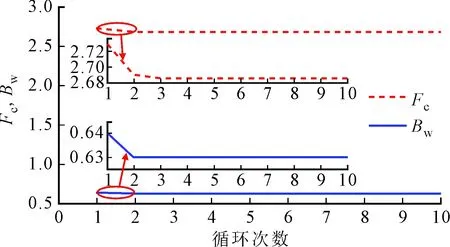
图11 不同循环次数对应的中心频率Fc和带宽Bw
图11给出了经过10次循环运算得到的Fc和Bw,发现两次循环之后频率值基本不变,故两次扫描循环后得到的带宽和中心频率即可达到最优。
5 故障轴承实验信号验证
采集轴承故障模拟实验台的振动信号,并利用本文所提方法做进一步处理。图12为轴承故障模拟实验台,轴承型号6307,电机转速为1 496 r/min,采样频率Fs为15 360 Hz,采样点数N为6 192。表1给出了该轴承对应的故障特征频率。
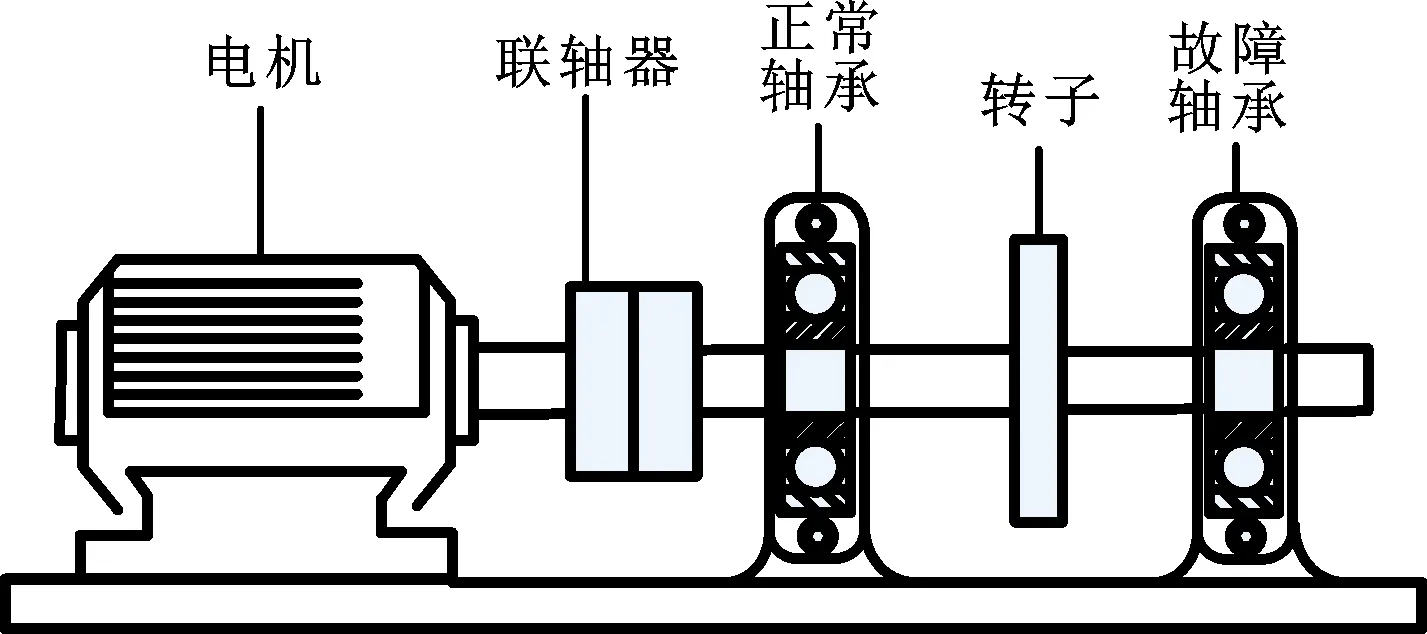
图12 轴承故障模拟实验台

内圈转频fr/Hz外圈故障特征频率fo/Hz内圈故障特征频率fi/Hz滚动体故障特征频率fb/Hz24.9376.73122.7451.17
轴承外圈故障振动信号及其频谱如图13所示,发现2 000 Hz左右出现共振频带。用ASNE方法对该信号进行两次扫描滤波处理,初始带宽设置为300 Hz,Δb1与Δf1均设为50 Hz。实验结果如图14所示,得到精确的中心频率为1 916.25 Hz,带宽为715 Hz。
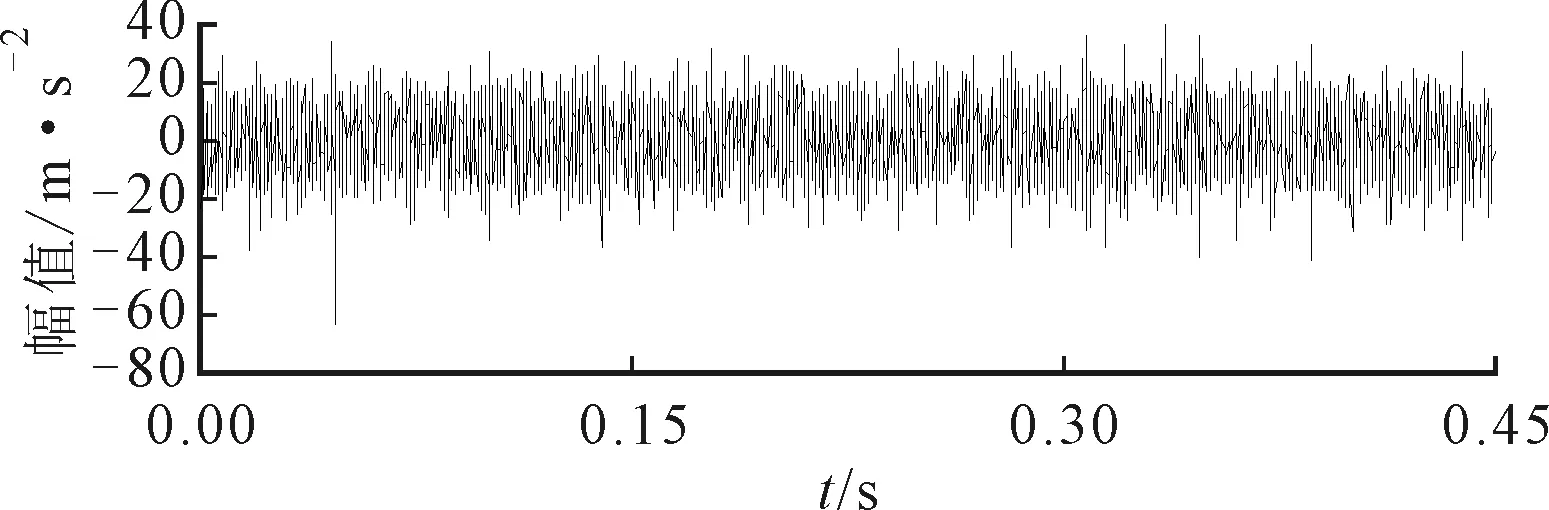
(a)振动信号
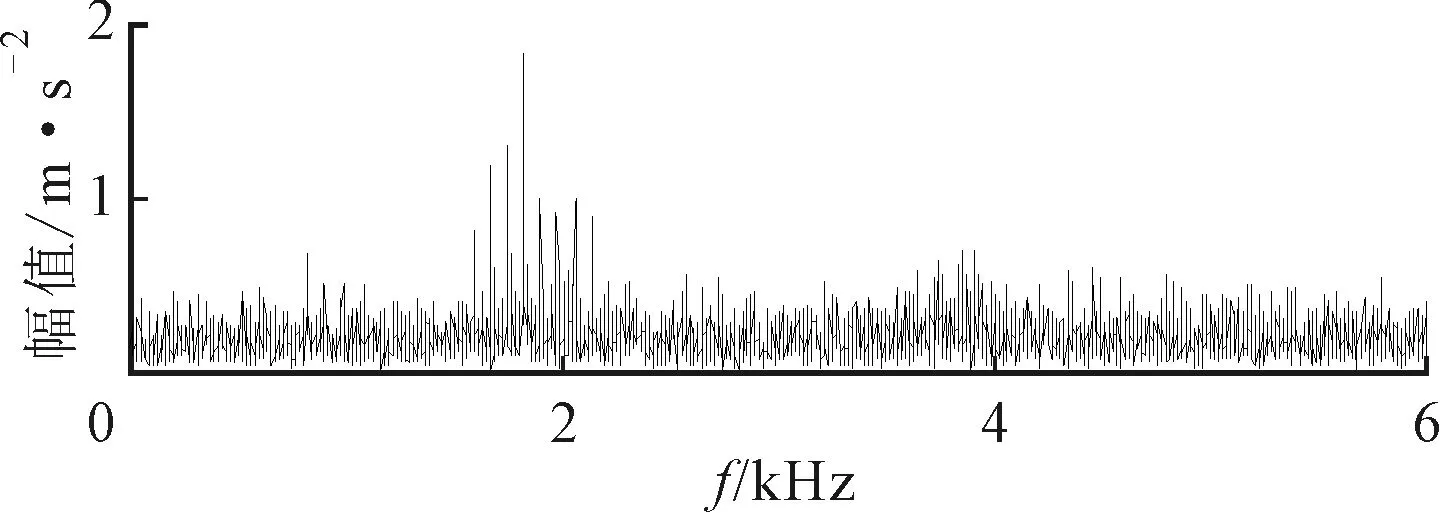
(b)频谱图13 轴承外圈故障振动信号及其频谱
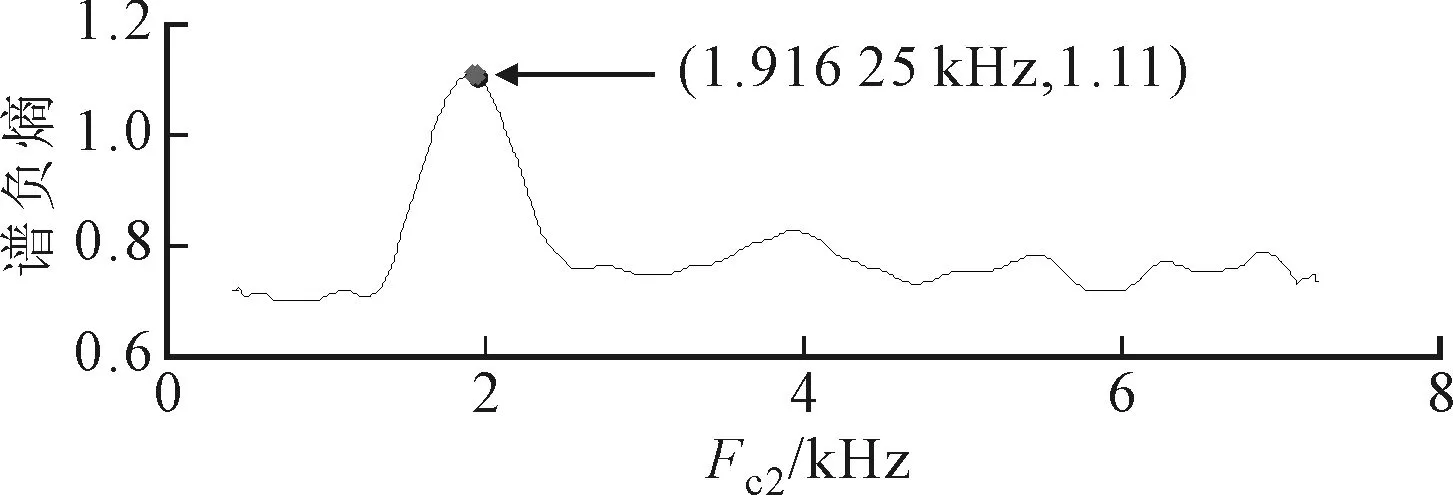
(a)固定带宽
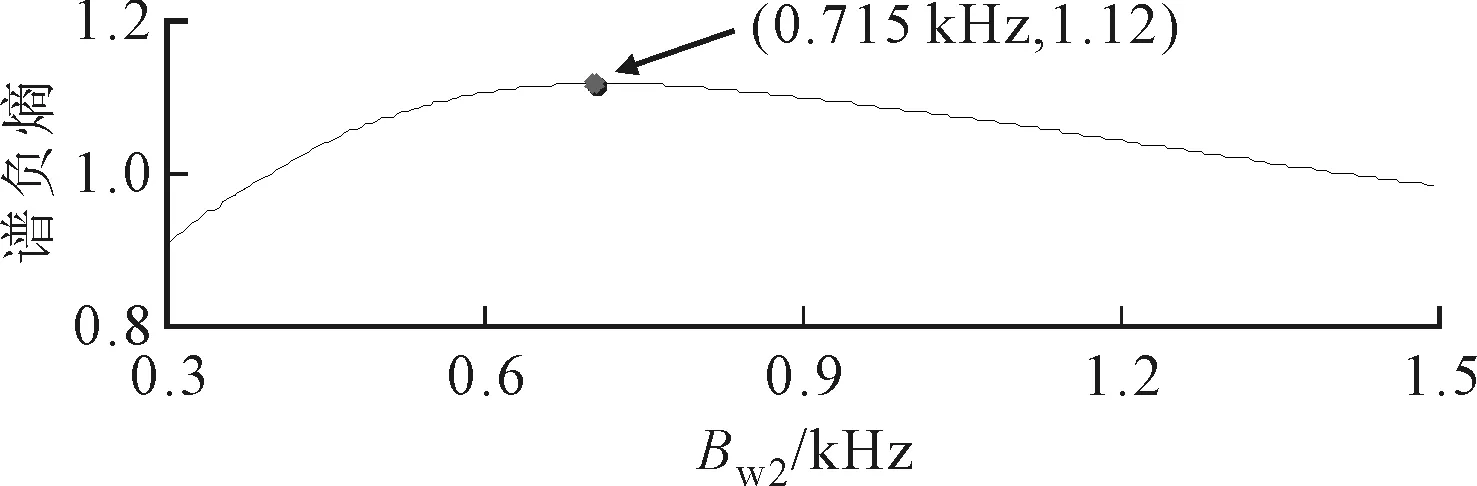
(b)固定中心频率图14 精确故障带宽和中心频率扫描谱负熵曲线
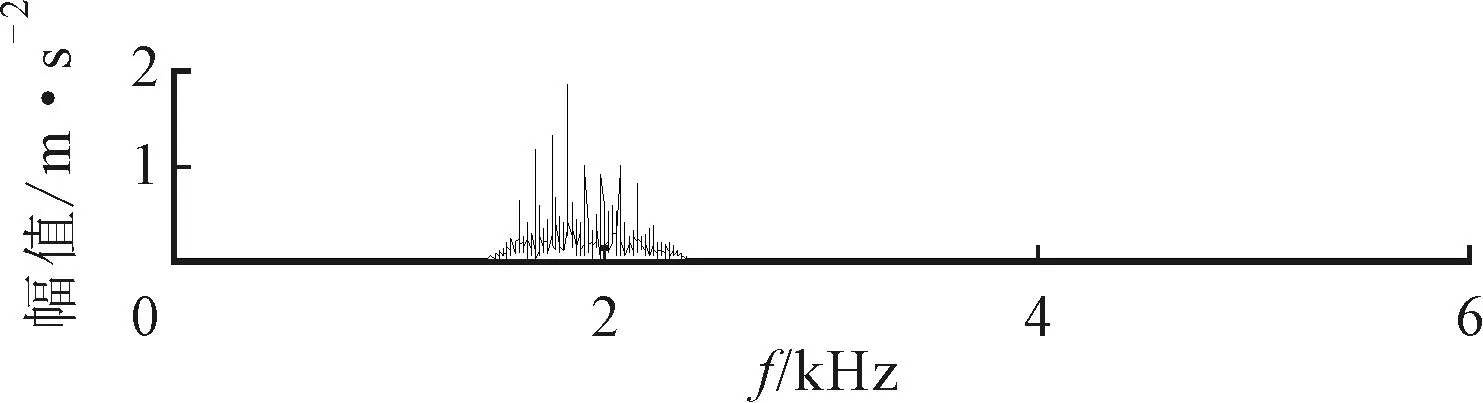
(b)频谱
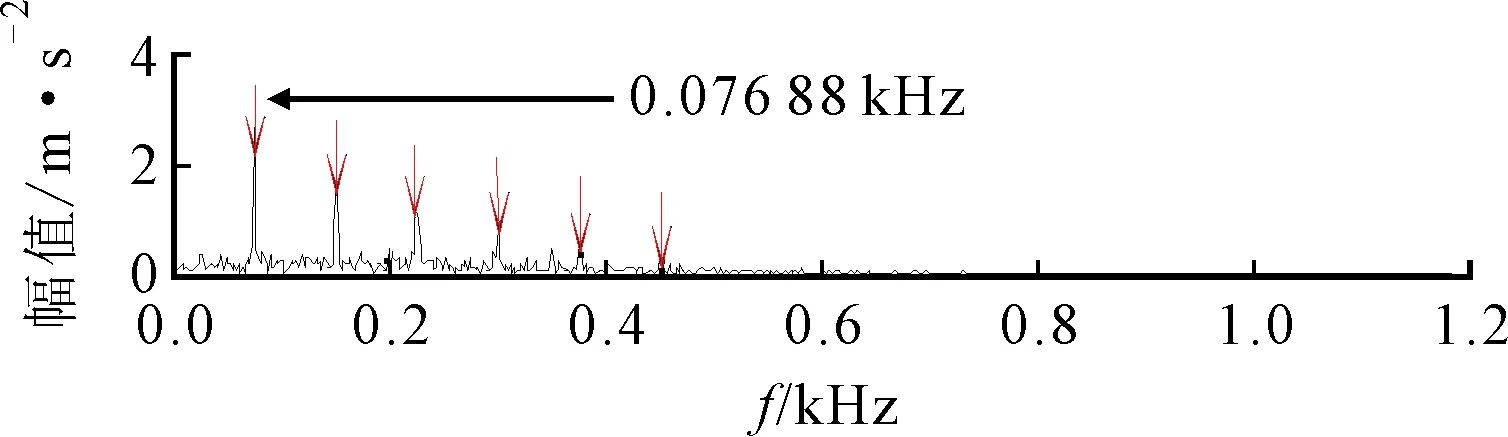
(c)包络谱图15 外圈故障特征提取分量
图15为故障特征提取分量的波形、频谱及包络谱。由图15中的波形可以看出,该分量存在明显的周期性冲击特征,而频谱中,边频带成分也被很好地提取出来,同时包络谱中出现了76.88 Hz及其2~6倍频,十分接近外圈故障频率fo。图16给出了利
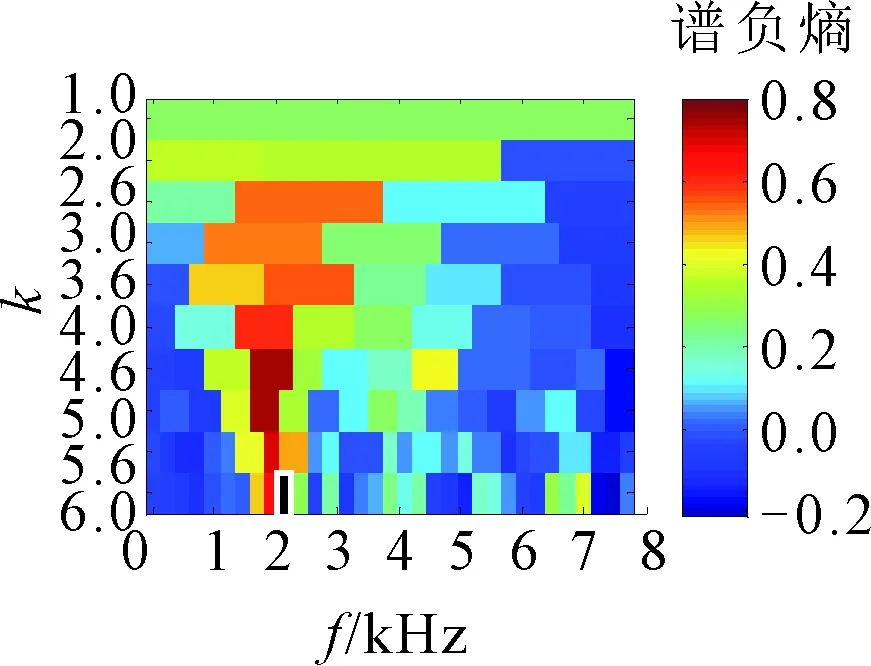
(a)ΔIε
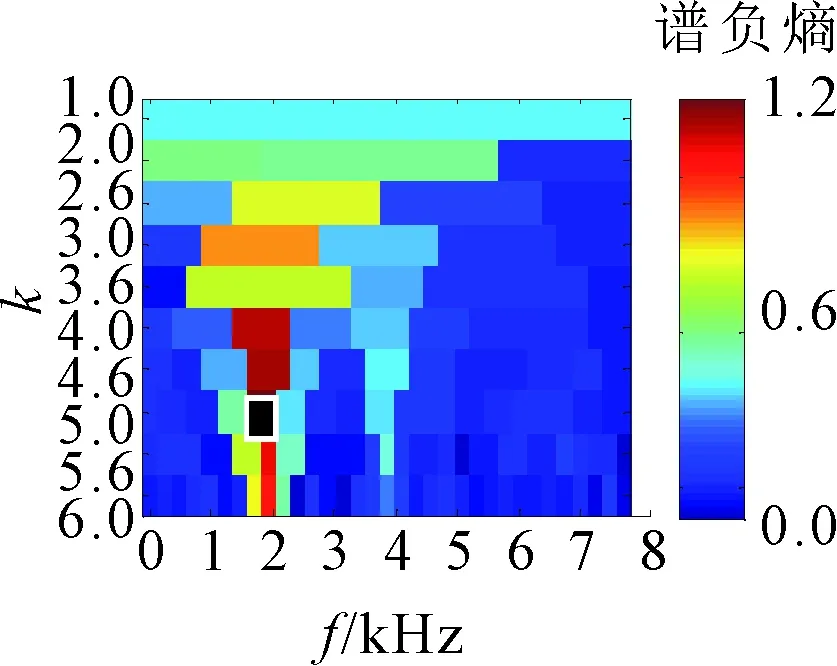
(b)ΔIE
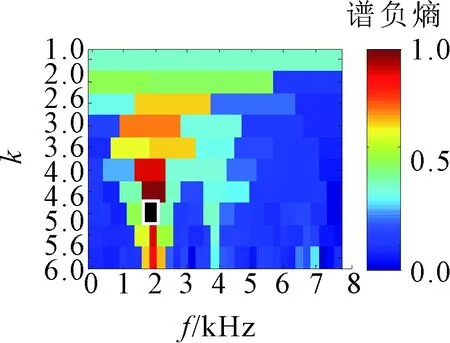
(c)ΔI1/2图16 Infogram方法处理的轴承外圈故障结果
用Infogram方法对同一信号进行处理的结果,3个二维图分别表示时域谱负熵ΔIε、频域谱负熵ΔIE和平均谱负熵ΔI1/2。
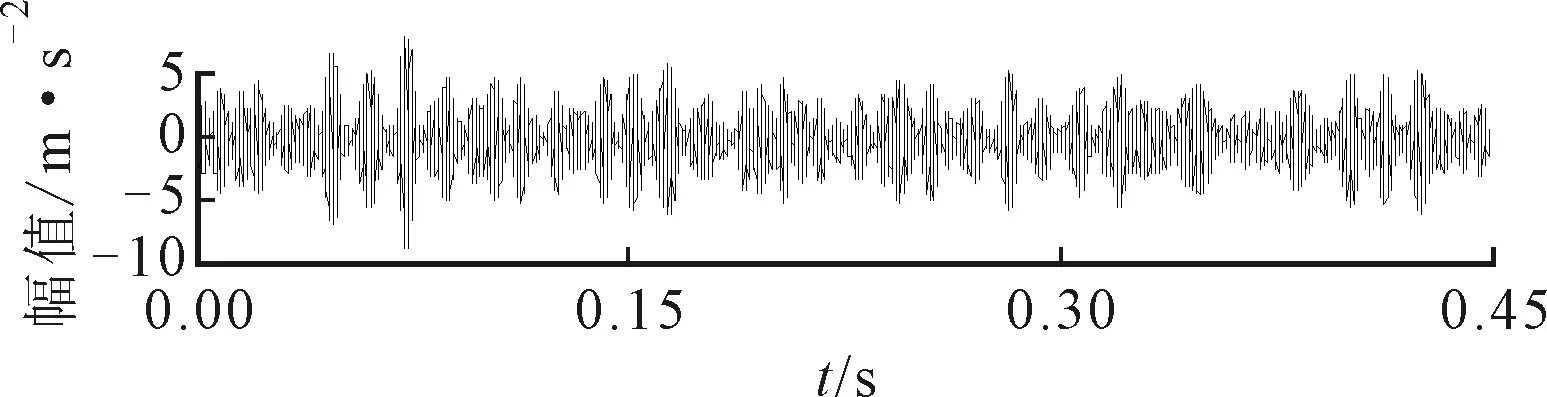
(a)波形
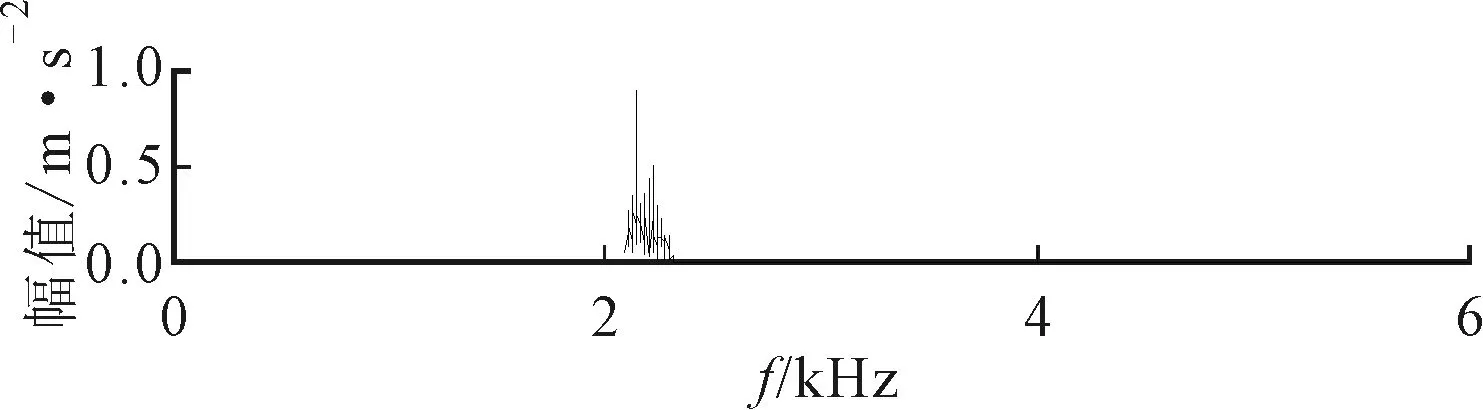
(b)频谱

(c)包络谱图17 外圈故障SE负熵提取的分量
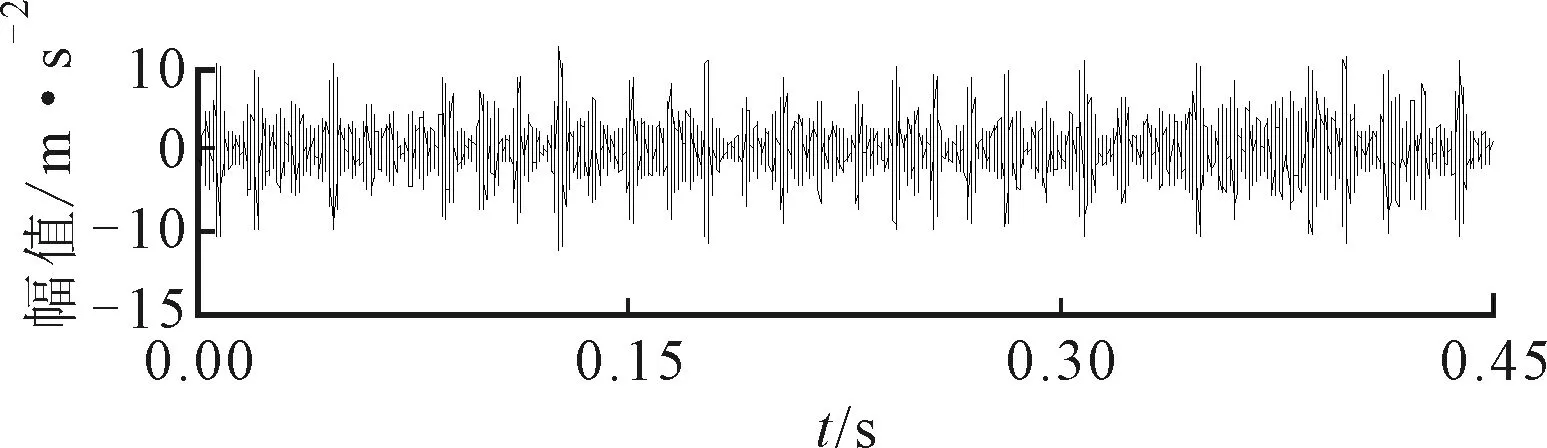
(a)波形
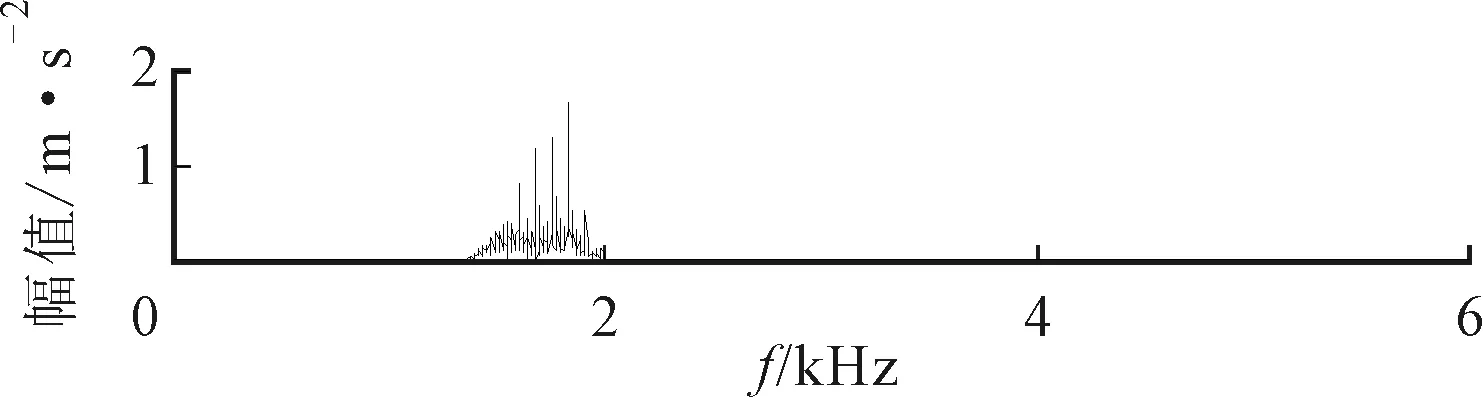
(b)频谱
受噪声影响,ΔIε确定的中心频率和带宽分别为2 160 Hz和240 Hz,对该频段进行分量提取,得到如图17所示结果。图17中的周期性冲击远没有图15中明显,而且得到的包络谱中只能发现故障特征频率的1倍频。图16中ΔIE和ΔI1/2确定的中心频率和带宽分别为1 680 Hz和480 Hz,对该频段进行分量提取得到的结果如图18所示。由图18可见,时域波形中包含的周期性冲击特征较明显,但是其频带宽度较窄,包络谱中包含的外圈故障频率仅有1~3倍频,且噪声相对较强,提取效果比精细谱负熵差。
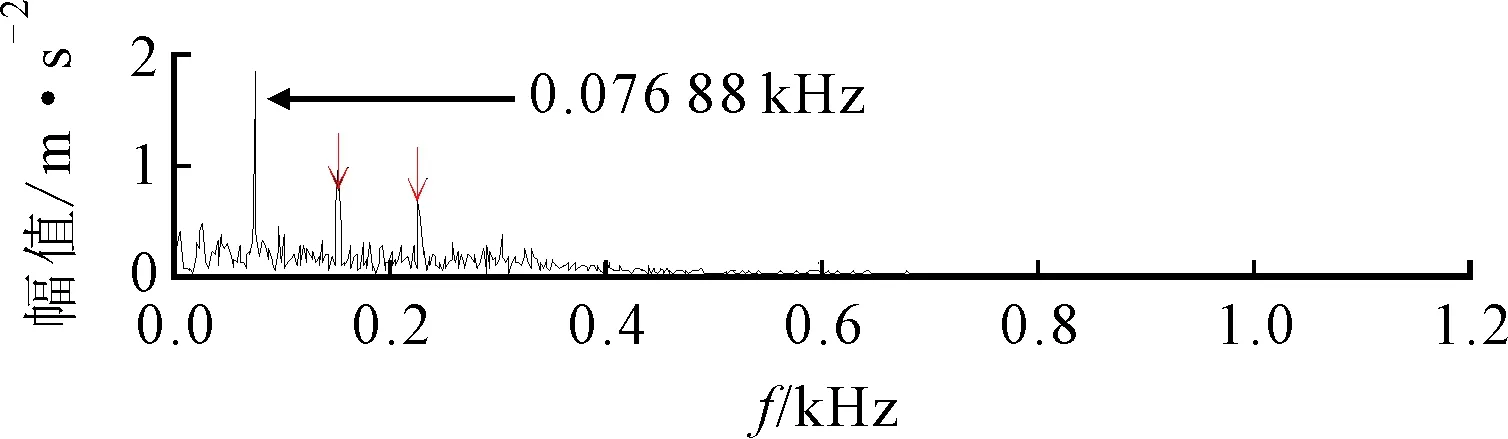
(c)包络谱图18 外圈故障SES、平均谱负熵提取的分量
(a)波形

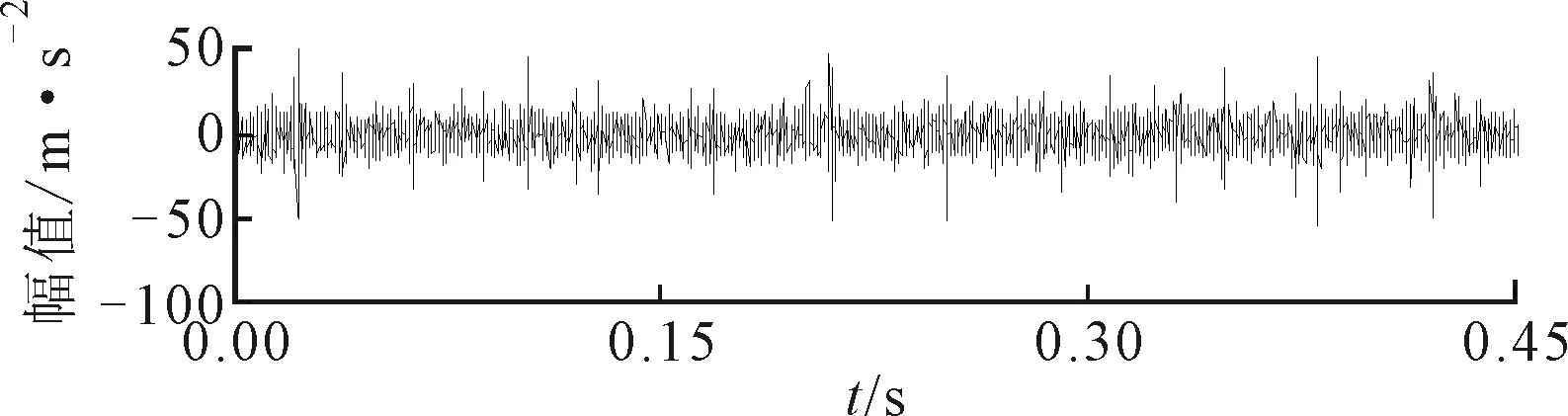
(b)频谱图19 轴承内圈故障振动信号波形及其频谱
(a)固定带宽

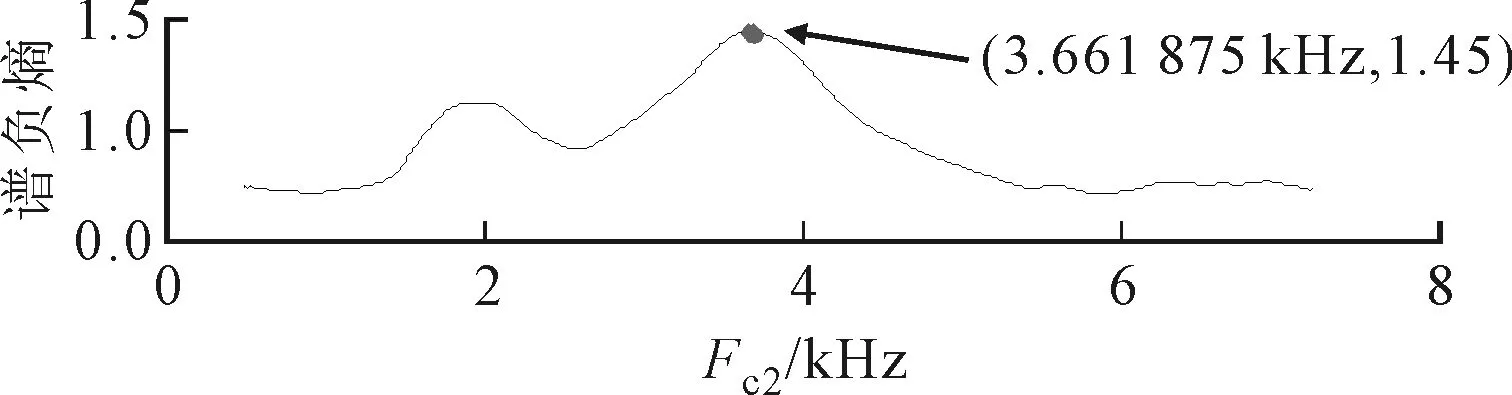
(b)固定中心频率图20 内圈故障带宽和中心频率扫描谱负熵曲线
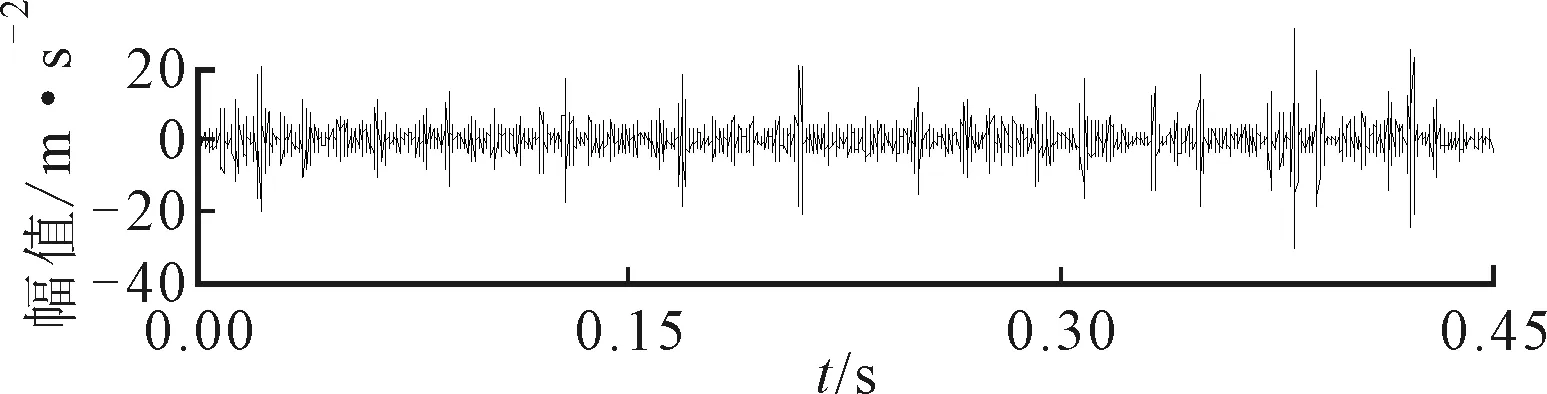
(a)波形
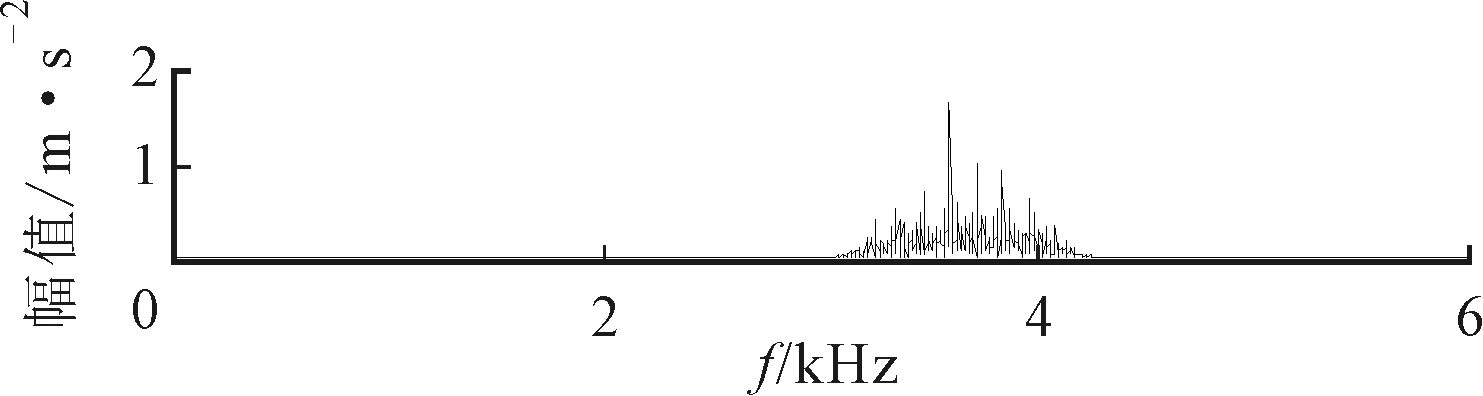
(b)频谱
(c)包络谱图21 内圈故障特征提取分量
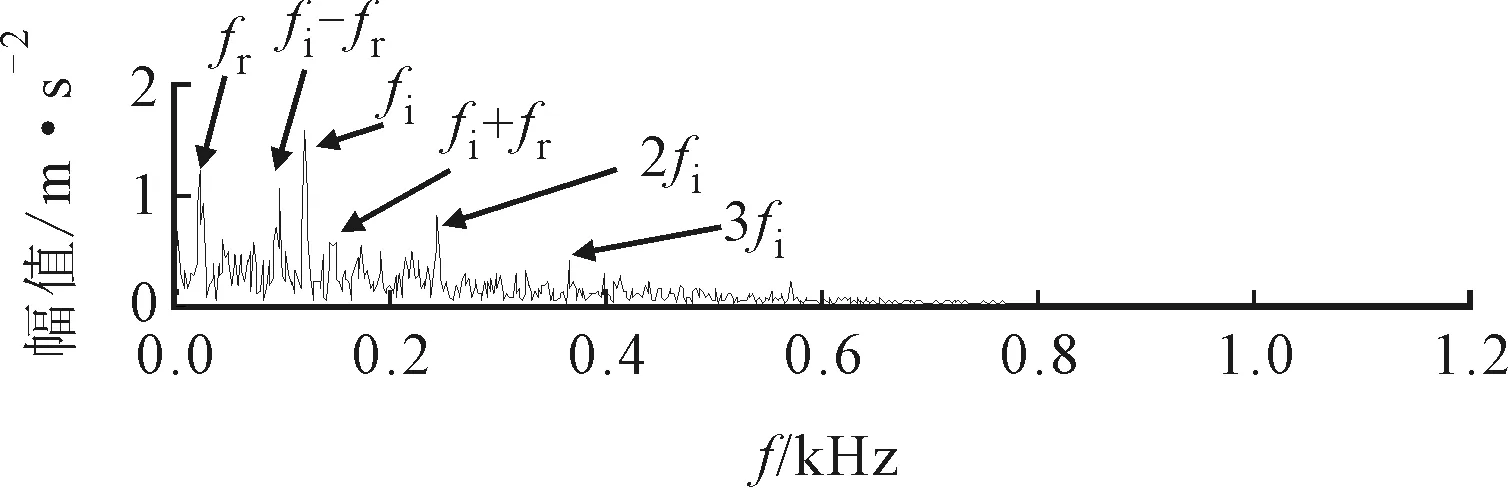
相同转速下,对6307轴承内圈故障振动信号进行分析,得到轴承内圈故障振动信号波形及其频谱如图19所示。采用ASNE方法(参数设置外圈)得到内圈最适中心频率和带宽分别为3.661 875 kHz与0.94 kHz,如图20所示。图21给出了对应提取的故障特征分量,包络谱中发现频率fr=24.38 Hz(理论值24.93 Hz)和内圈故障特征频率fi=121.9 Hz(理论值122.74 Hz)。同时还清晰地发现fi的2、3倍频,以及内圈与转频的调制频率fi-fr与fi+fr。同样采用Infogram方法处理轴承内圈故障振动信号,得到如图22所示结果。对相应频带区域进行提取,观察图23与图24中间部分的频谱不难发现,两个频带宽度都比ASNE方法得到的带宽要宽。

(a)ΔIε

(b)ΔIE
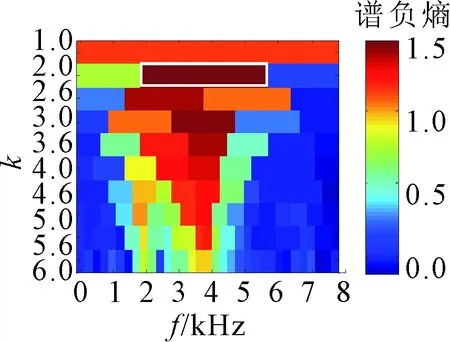
(c)ΔI1/2图22 Infogram方法处理的轴承内圈故障结果
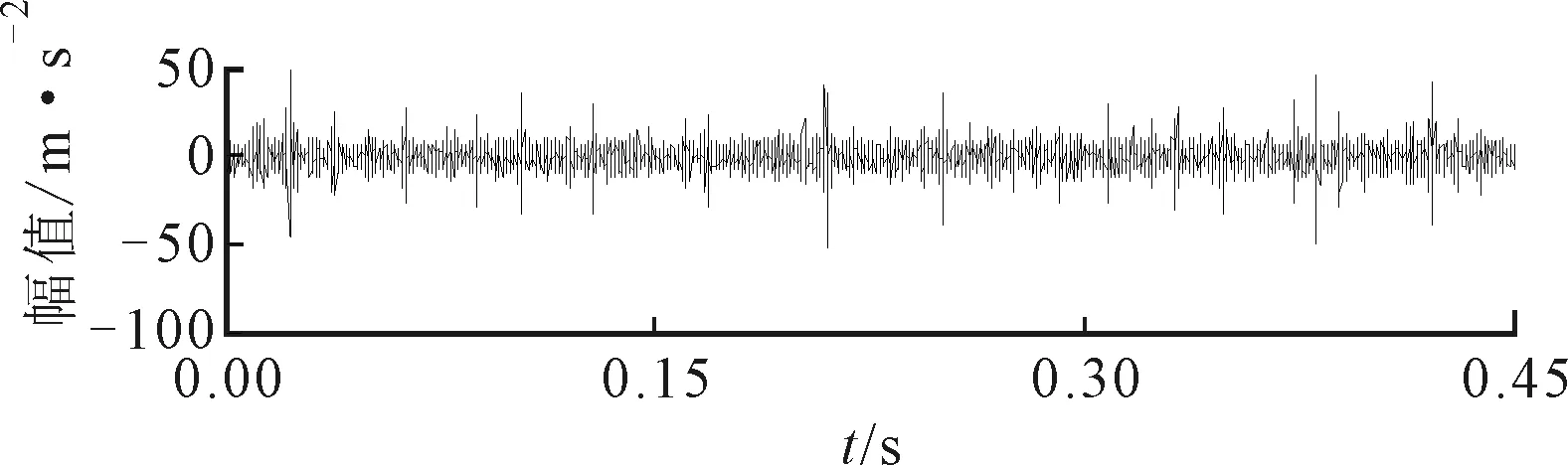
(a)波形
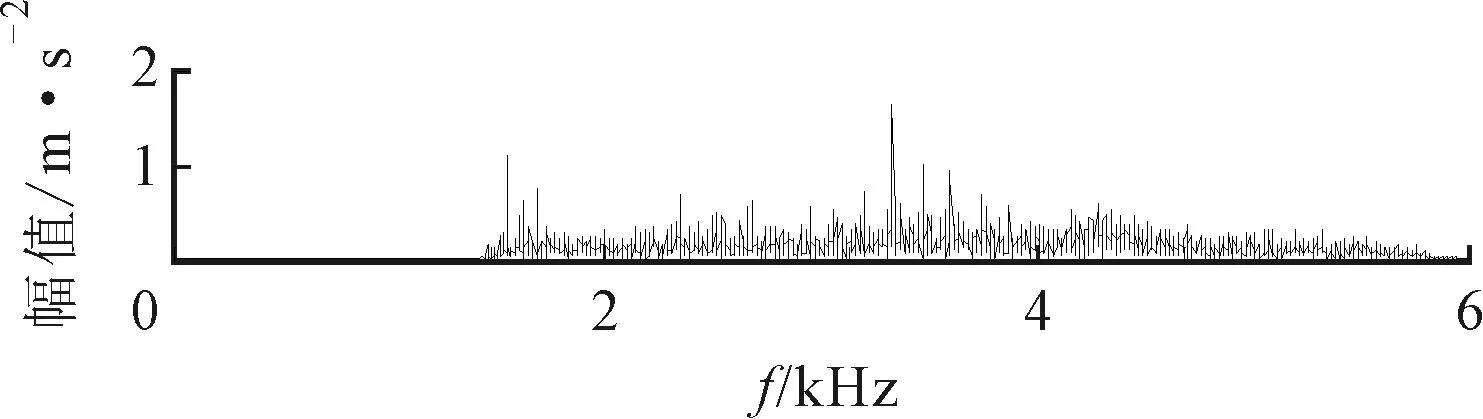
(b)频谱
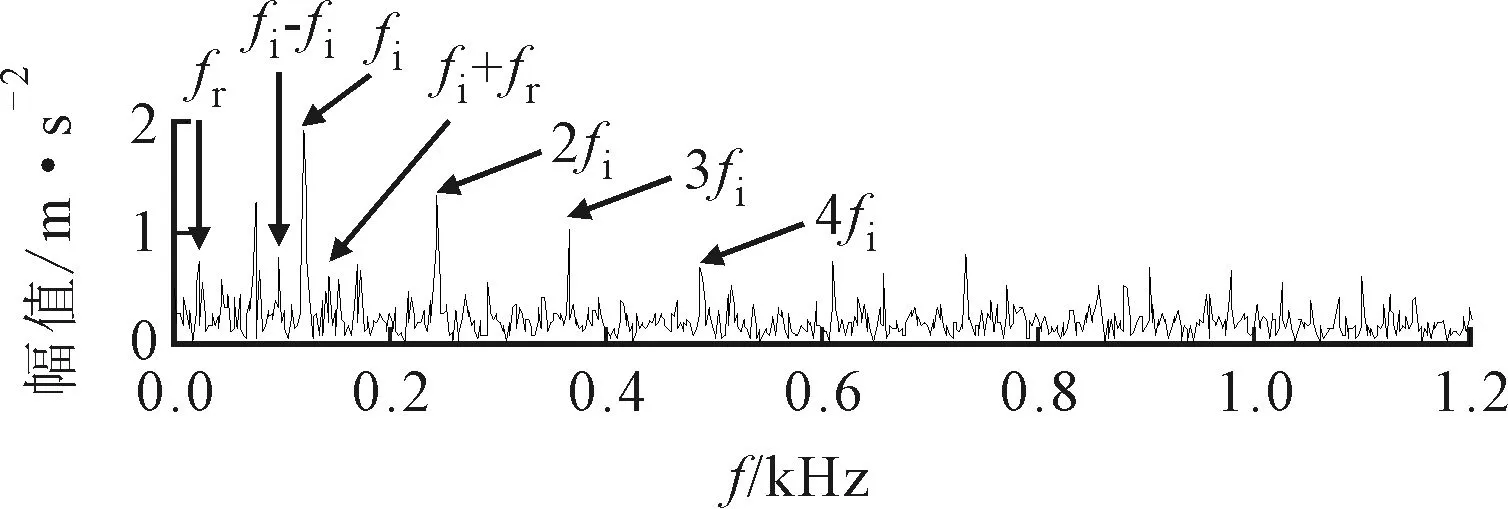
(c)包络谱图23 内圈故障SE负熵提取的分量
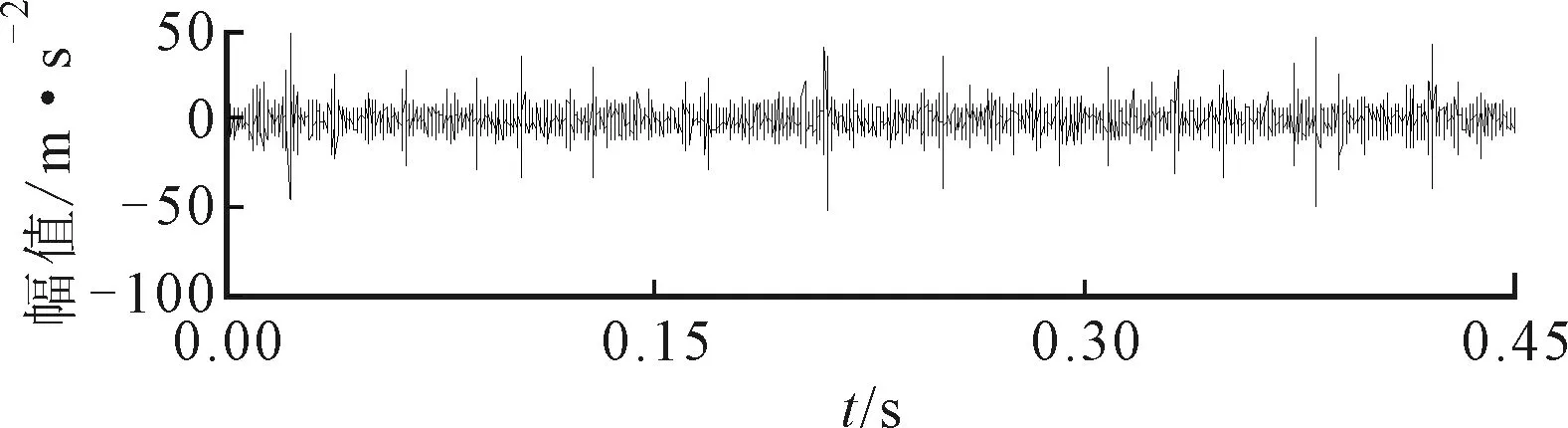
(a)波形
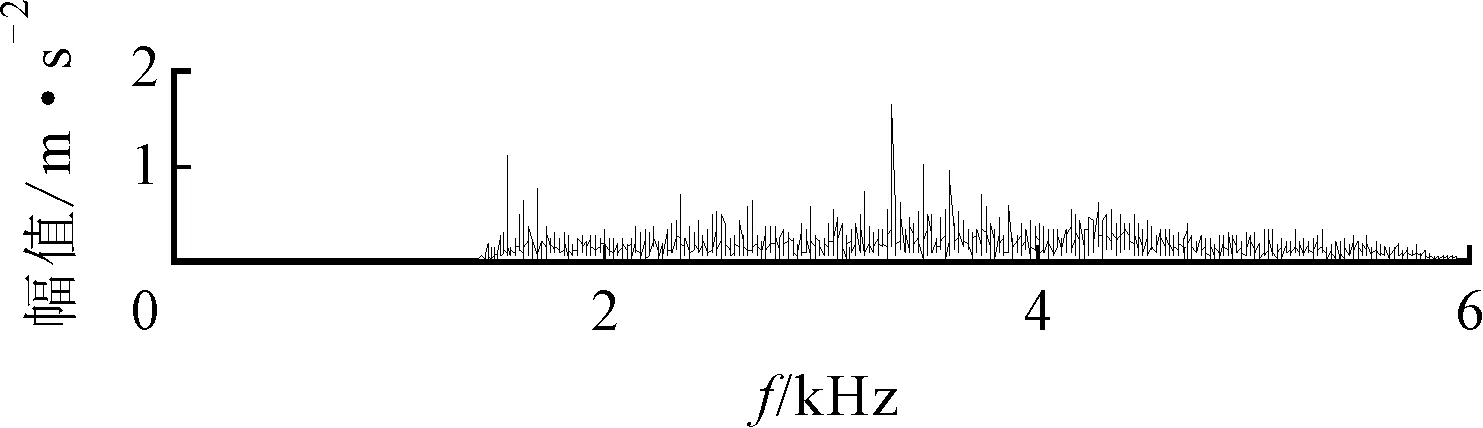
(b)频谱

(c)包络谱图24 内圈故障SES、平均谱负熵提取的分量
如图23所示由ΔIε提取的特征分量中包含较少噪声成分,因此其包络谱中也能找到fr、fi及其倍频,以及出现fr与fi调制的现象,但比ASNE方法得到的分量包含了较多的干扰频率。由ΔIE和ΔI1/2提取的特征分量,如图24所示,其频谱中包含了更多的干扰频率,可能会影响诊断结果。实验结果表明:ASNE方法能有效地确定轴承振动信号中的边频带,提取包含更为丰富的故障特征信息,更利于实现轴承故障的诊断。
6 结 论
本文利用谱负熵ΔIx作为筛选指标,通过对信号ΔIx较大的频带进行筛选,得到包含故障信息较多的特征分量,有效地排除噪声的干扰。同时结合经验小波变换原理,利用其滤波器构造方法,构造变带宽的扫描滤波器,实现对振动信号整个频段的扫描滤波,以找到最合适的中心频率和带宽。该方法能够自适应地识别轴承故障频率对应的频带范围,获得更为准确的共振边频带,并对故障特征分量进行提取,通过对仿真信号和实验信号进行分析,充分证明了其有效性,该方法的提取效果优于Infogram方法,更容易实现滚动轴承的故障诊断。
ΔIx对偶然冲击也比较敏感,如果处理的轴承振动信号中存在较强的偶然冲击,可能会影响故障特征频率的提取效果,从而影响轴承故障类型的判断,因此后续要寻找一个新指标,来改进精细谱负熵方法,使其既可以避开偶然冲击的干扰,又可以获得更为精确的中心频率和带宽,从而广泛应用于轴承故障诊断领域。
