采用同步压缩变换和能量熵的机器人加工颤振监测方法

薛雷,曾宏伟,覃程锦,陶建峰,刘成良,汤海洋,黄稳

(1.上海飞机制造有限公司,200240,上海; 2.上海交通大学机械系统与振动国家重点实验室,200240,上海)

在航空以及汽车制造等机械制造业中,由于零件尺寸更大,结构和工艺更为复杂,传统的加工机床难以适应其加工要求。相比之下,机器人加工系统具有灵活性好、效率高以及加工空间大等优势[1]。然而,工业机器人通常采用多杆串联型结构,使得其系统刚度远远低于传统机床[2-3]。因此,在机器人加工过程中,系统极易产生颤振,导致工件加工质量降低以及刀具寿命缩短,甚至会造成机器人损坏[4-6]。为避免颤振带来的危害,可以在颤振发展的早期对机器人加工系统进行干预,通过调整加工参数等措施抑制颤振进一步发展。因此,实时监测加工系统的状态,在颤振发展的早期尽快将其检测出来显得尤为重要。

传感器是从加工系统获取物理信息的桥梁。目前,多种传感器信号被获取用于颤振的监测与分析,包括切削力信号[7]、声信号[8]、电机电流信号[9-10]和振动信号[11-12]等。由于颤振是一种自激振动,振动信号能更好地反映颤振发展的过程,且其具有低成本和易获取的优势,是一种较为理想的颤振监测信号。原始的传感器信号往往难以直观反映颤振的产生,需对其加工处理才能获取有用信息。常用的信号处理方法有时域分析、频域分析以及时频分析。时域分析和频域分析一般用于平稳信号的处理,而机械加工过程中振动信号多为非平稳信号,因此时频分析方法更能有效地分析颤振信号。Liu等[10]利用经验模态分解法分析电机电流信号,然后进行颤振特征提取;Yao等[13]对振动信号进行小波变换,再通过支持向量机进行特征分类;Liu等[14]提出了基于变分模式分解的铣削颤振监测方法。然而,这些经典的时频分析方法受限于海森堡不确定性原理,无法在时间和频率上同时到达很高的分辨率,使得颤振监测的准确度受限。为获取更高分辨率的时频谱,Daubechies等[15]提出了同步压缩变换(SST),该方法在传统时频分析结果上,利用同步压缩算法将具有相同瞬时频率的时频系数压缩至它们的瞬时频率处,使得频率曲线更加集中,从而提高了时频谱的分辨率,并且SST支持信号重构,是一种分析非平稳信号的有效工具。

机器人加工时往往伴随着刀具与工件之间的相互振动。加工平稳时以强迫振动为主,振动频率通常为主轴旋转频率、齿通频率及其倍频,幅值较小。当加工变得不稳定时,系统会发生颤振,此时自激振动占据主导地位,振动频率接近或等于系统固有频率,振幅显著增大[16-17]。加工振动与颤振之间存在过渡阶段,目前暂无公认的指标可直接区分颤振和正常加工振动。因此,寻求对颤振敏感的特征量是实现颤振在线自动监测的关键。由于加工振动和颤振之间存在振动频率及幅值方面的差异,颤振的发展过程中通常会伴随着振动频率分量以及能量分布的变化,设法捕捉这种变化为颤振自动辨识提供了思路。近年来,能量熵引起了人们的关注,由于其能很好地描述非平稳信号能量分布的变化,在机械故障诊断[18]和机床铣削状态分析[19-20]中都得到了应用。

基于以上分析,本文提出了基于同步压缩变换和能量熵的颤振监测方法。首先,通过同步压缩短时傅里叶变换获得振动信号的高分辨率时频描述,再将信号分为多个频带,重构得到各频带的子信号,然后引入能量熵作为颤振监测的特征量,最后求取子信号能量熵之和以实现机器人加工颤振的在线监测。

1 机器人加工颤振监测算法

1.1 同步压缩变换

同步压缩变换是一种时频后处理方法,旨在提高时频谱的分辨率。SST的基本原理是:在原始线性时频谱的基础上对线性时频变换结果进行重排,将具有相同瞬时频率的时频系数压缩到它们的瞬时频率位置,以获得更加准确和清晰的时频谱。下面以短时傅里叶变换(STFT)为例,对SST算法进行说明。

对时域信号x(t)进行短时傅里叶变换,可得其时频谱为

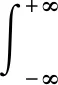
(1)

式中:u为窗长;g(u-t)为可随时间t移动的紧支窗函数。窗函数g用于截取时域信号x(t),对截取后的信号进行傅里叶变换,就能得到t时刻信号x的局部频谱信息。当窗函数沿整个时间轴移动时,就能得到信号x完整的时频分布。

将x(t)的STFT公式乘上一个相位因子eiω t,可以得到调整相位后的信号时频谱

(2)

若x(t)是幅值为A、频率为ω0的谐波信号,即x(t)=Aeiω0t,对x(t)进行傅里叶变换,可得

(3)

(4)

从式(4)可以看出,谐波信号x(t)经STFT后的时频谱,时频系数的峰值出现在谐波信号频率ω0处,分布于ω0两侧的时频系数则随跟ω0的距离增大而减小。可见,虽然信号经STFT变换后时频系数分布于瞬时频率附近,但窗函数存在能量泄露导致时频谱模糊,降低了时频谱的分辨率。

信号的瞬时频率ω0可以通过下式计算

(5)

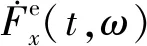
(6)

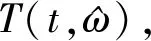
(7)

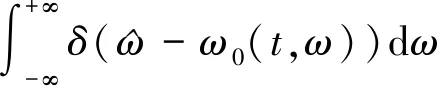
1.2 机器人加工颤振监测算法

颤振是加工过程中机器人结构从周期性切削力中吸收能量而产生的自激振动。当机器人加工系统从平稳加工阶段过渡到颤振阶段时,振动信号中会产生新的主频分量,并且能量向颤振频率处转移。因此,可以通过监测振动频率分量及其能量分布变化来实现颤振的监测。根据上述分析,提出了基于SST的机器人加工颤振监测算法。首先,通过SST得到高分辨率的时频谱,假设加工过程中实际测得的振动信号为s(t),则其SST谱可以表示为

(8)

式中:ω0为瞬时频率,可根据式(6)计算,即

(9)

由于计算机在计算过程会存在误差,在编程计算时,可设定一个允许范围内的误差值ε,则式(8)可以根据下式近似计算

(10)

式中:ε通常取频率分辨率的1/2。

通过上述同步压缩短时傅里叶变换,获得了振动信号的高分辨率时频谱。为实现颤振监测,需利用特征量对能量分布变化进行表征。熵能够度量系统的混乱程度,因而引入能量熵作为描述能量分布变化的特征量。

为计算系统的能量熵,先将SST谱划分为有限数量的频带,再通过重构公式计算每个频带对应的时域子信号,重构过程为

(11)

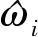
对于每个重构子信号,其能量计算公式为

(12)

则系统加工过程的能量熵H为

(13)

能量熵H即为用于颤振监测的特征量。颤振发生时,能量向颤振频率处转移,系统能量熵H会快速增加。因此,可以通过实时计算振动信号的能量熵H进行颤振的在线监测。在大量机器人加工实验的基础上,预先确定一个用于颤振判别的能量熵阈值,然后实时计算机器人加工过程中振动信号的能量熵并与阈值比较。当能量熵超过颤振阈值时,则说明识别出了颤振,需要采取主动抑振措施。

需要指出的是,能量熵阈值的选取对颤振辨识结果具有重要影响。阈值过高会导致辨识时间滞后,无法保证在颤振初期将其识别出来。阈值过低则会使得鲁棒性变差,容易造成误报。因此,能量熵阈值的选取应在保证高辨识准确度的前提下,同时使识别出颤振的时间尽可能早。

2 实验验证

2.1 实验平台

为验证所提算法对机器人加工颤振监测的实际效果,搭建了如图1所示的机器人加工实验平台。该平台主要由库卡工业机器人、末端执行器、工件及夹具、传感器以及数据采集系统组成。末端执行器通过法兰安装在机械臂末端,主要包括主轴单元、进给单元、视觉测量模块、法线测量模块以及压脚。机器人进行加工时,首先采用视觉测量模块进行参考孔定位,然后通过压脚压紧工件,利用主轴单元和进给单元实现加工操作。

图1 机器人加工实验平台

为测量机器人加工过程中主轴振动信号,选用型号为PCB 356A24的加速度计,将其安装在主轴上,如图2所示。数据采集系统以10 240 Hz的采样频率实时采集振动加速度信号。实验过程中,采用了两种不同几何形状的硬质合金钢钻锪刀具,其中刀具Ⅰ直径为6 mm,顶角为120°,锪孔角度为100°;刀具Ⅱ直径为5 mm,顶角为130°,锪孔角度为100°。

图2 刀具及加速度计安装实景

2.2 实验结果

基于上述实验平台,开展了一系列不同加工参数下的加工实验。分别对AL6061和AL7075两种航空铝合金工件进行了制孔加工实验,所有加工过程均未使用润滑剂和冷却液。为避免偶然因素对实验结果造成影响,每组相同工艺参数的实验均重复进行3次。

为确定一个合理的颤振辨识阈值,共进行了480次机器人加工实验,涉及不同的刀具、工件材料和切削参数,通过观察加工孔的表面质量选出了其中存在颤振现象的实验数据进行分析。将选取的数据分成两个部分:一部分用于阈值的确定;另一部分用于验证阈值的合理性。确定阈值时,先结合振动幅值变化以及频谱近似确定颤振发生的时间,然后计算对应时刻的能量熵值,经过对大量实验数据的处理,从中总结出一个较为合理的阈值。为保证阈值的合理性和适用性,用另一部分数据对其进行验证,若无法满足要求则需重新选择。理论上来说,能量熵阈值大小与加工参数及机器人位姿存在一定关系。在本实验中,主轴转速从1 200 r/min增至4 500 r/min,进给速率从0.9 mm/s增至9.6 mm/s。通过对大量的实验数据分析发现,在此工艺参数范围内,颤振发生时系统能量熵变动幅度较小,始终维持在一个相对稳定的数值附近,最终确定阈值为105。需要指出的是,本实验中机器人姿态变化较小,暂未考虑大范围姿态变化对阈值的影响。

本文方法的在线监测过程为:对实验测得的振动信号,首先通过SST获取时频谱,然后将整个信号等分为16段频带,重构得到每个频带对应的时域子信号,最后计算能量熵对颤振进行监测。每隔25 ms执行一次,每次计算使用的信号长度为50 ms,采样频率为1.024 kHz时对应512个样本数据。单次能量熵计算所需时间约20 ms,基本能够满足颤振在线监测的实时性要求。将计算得到的能量熵值与阈值进行比较,一旦能量熵值超过阈值,则认为加工过程发生了颤振。

实验1采用刀具I对AL6061铝合金工件进行机器人加工实验,记录不同的主轴转速和进给速率下的振动信号和加工状态。为验证所提颤振监测算法的有效性,从出现颤振现象的实验中选取两组具有代表性的实验数据进行分析。主轴转速设为3 000 r/min,进给速率为3.5 mm/s,颤振监测结果如图3所示。图3b为振动信号的能量熵随时间变化的曲线,可以看到:能量熵在初始阶段数值较小且增长缓慢,而从约t=0.151 s开始曲线斜率变大,能量熵增长加快;在t=0.255 s时,能量熵超过阈值,颤振被检测出来;当t=0.5 s时,能量熵值已远远超过颤振发生前的数值,随后熵值又趋于平稳,可见能量熵能够很好地反映颤振发展的过程。从信号波形图3a来看,t=0.255 s时振幅较小,说明该时刻还处于颤振的萌芽阶段。观察SST谱图3c可以发现,直到t=0.289 s时颤振频率才变得明显。实验结果表明,本文提出的算法能在早期有效地识别出机器人加工系统颤振。

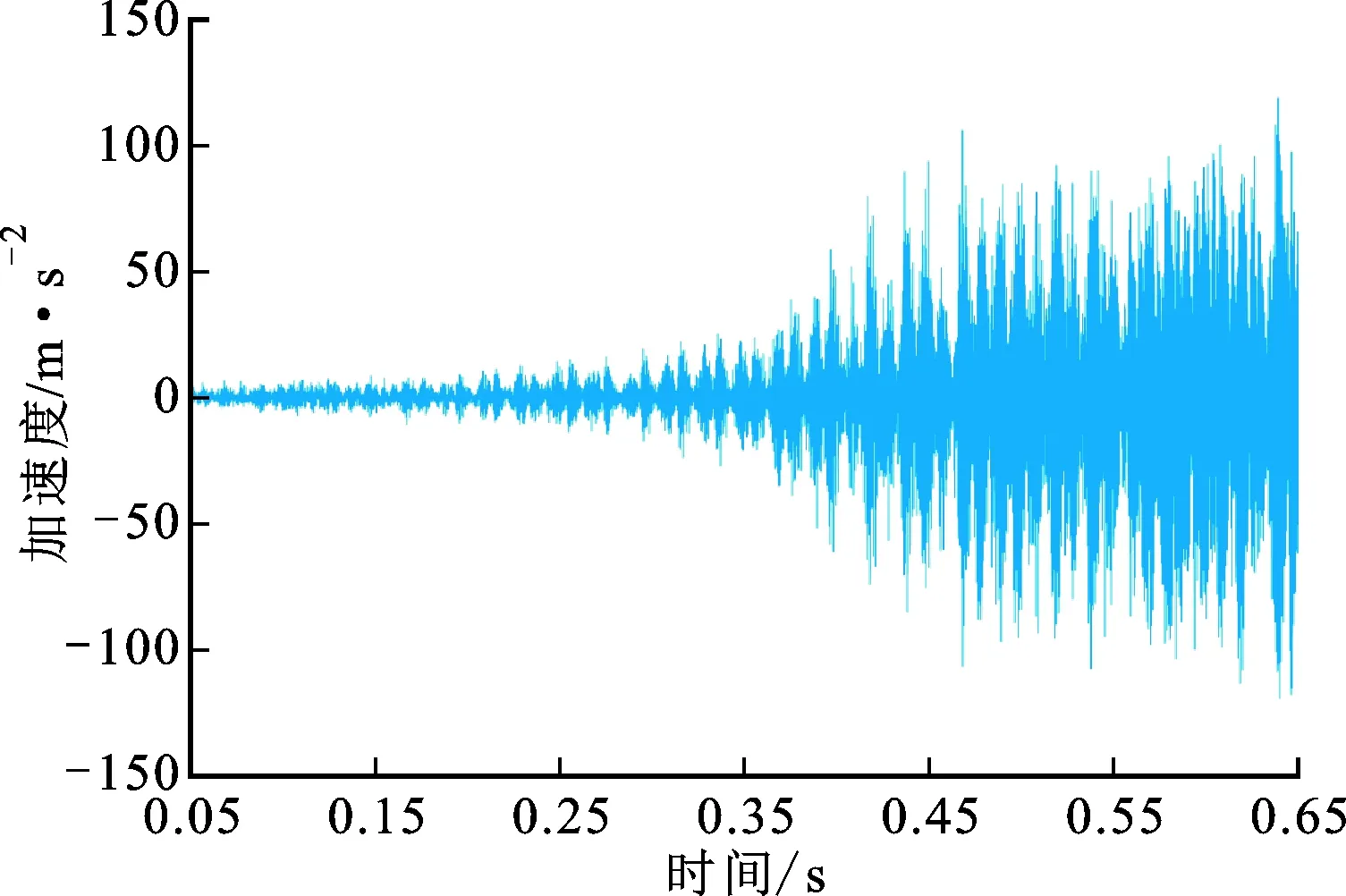
(a)振动时域波形

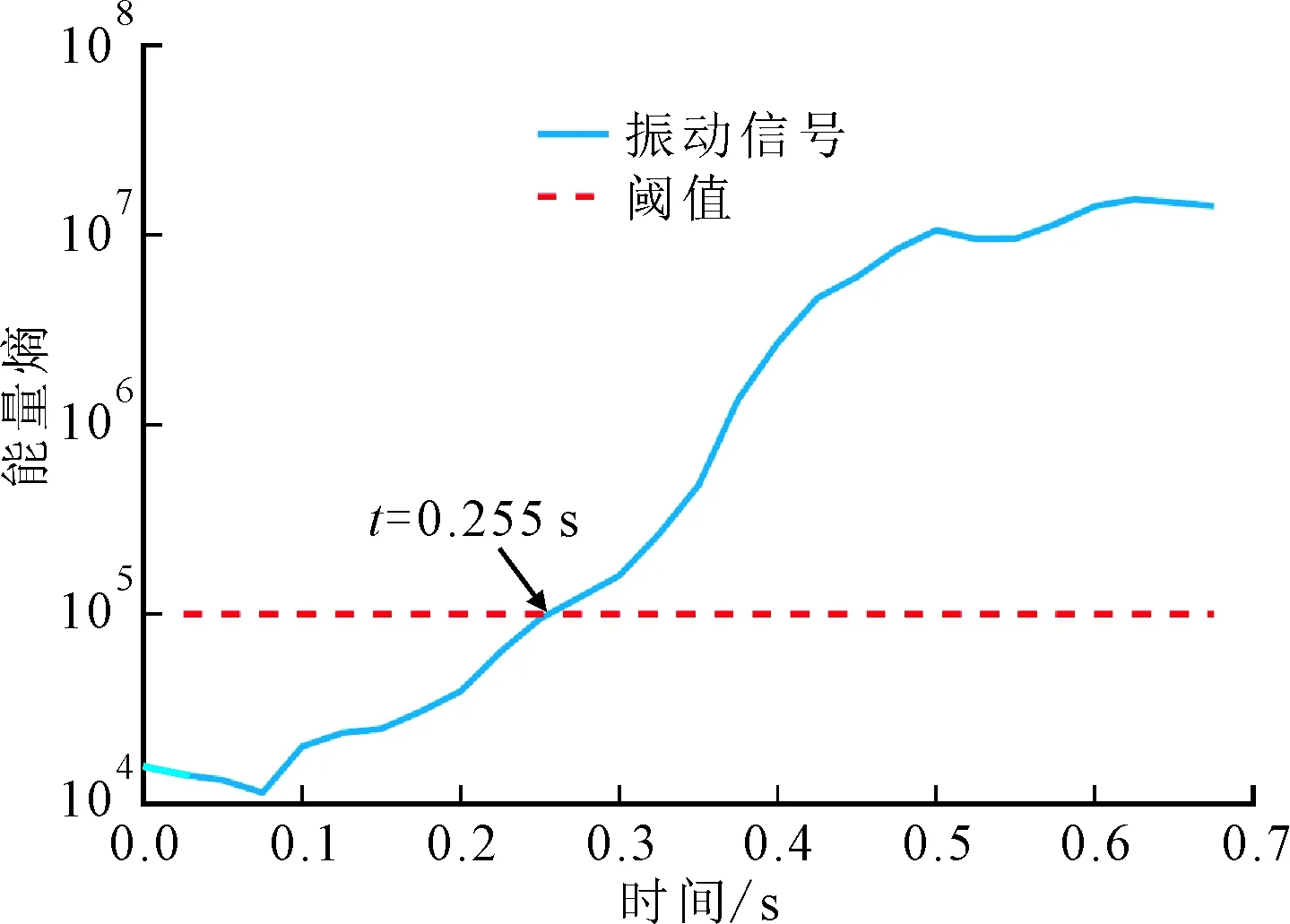
(b)能量熵曲线

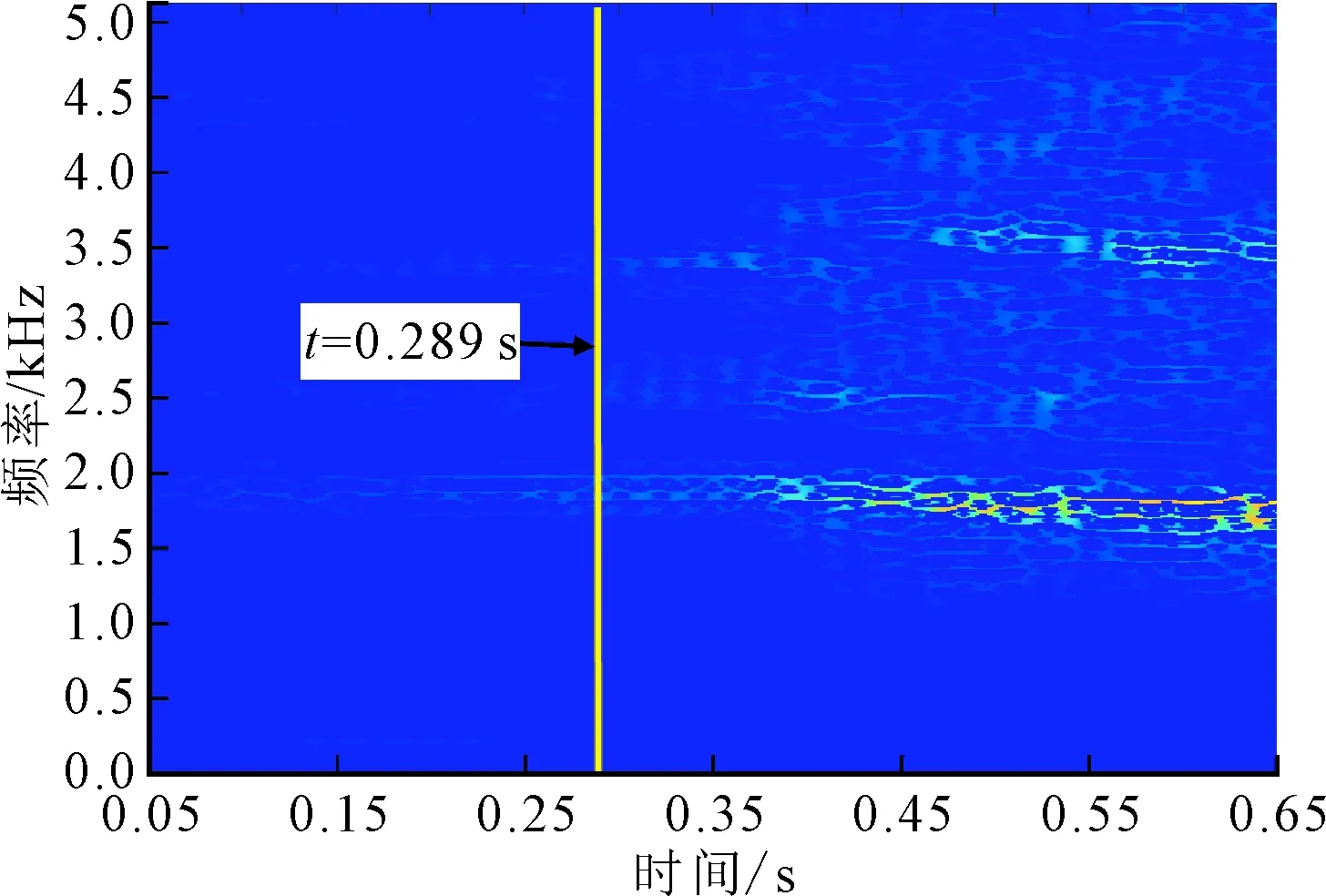
(c)SST谱图3 实验1的颤振监测结果

实验2刀具和工件材料同实验1,加工过程中主轴转速为3 000 r/min,进给速率为6.0 mm/s,颤振监测结果如图4所示。从图4b的能量熵变化曲线来看,振动信号能量熵在t=0.201 s前短暂上升,后随即减少,但未超过阈值。对照图4a的时域波形可以发现,在对应的时间段内振动幅度轻微增大后又减小。由此可见,能量熵对振幅变化较为敏感,同时也说明所选的颤振阈值是合理的。在t=0.250 s后能量熵快速增加,并于t=0.311 s时刻超过阈值,表明所提算法监测到了颤振。在大约t=0.432 s后,能量熵远远超过了初始值并变得相对稳定,说明此时颤振已经发展充分。颤振现象也能够观察时频谱中频率的变化来判断,从图4c的SST谱来看,相对明显的高频颤振频率分量出现在t=0.391 s时刻。同时,从图4a的时域波形可以看到,当所提算法监测到颤振时,振动幅值仍处于较低的水平,表明此时颤振才刚刚开始。因此,所提颤振监测算法能够在颤振发展的初期将其有效检测出来。

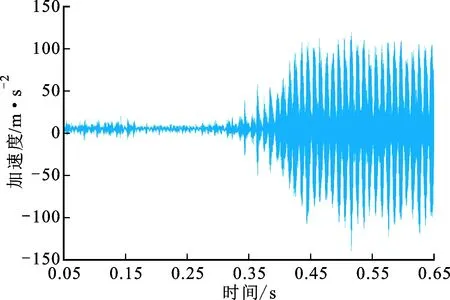
(a)振动时域波形

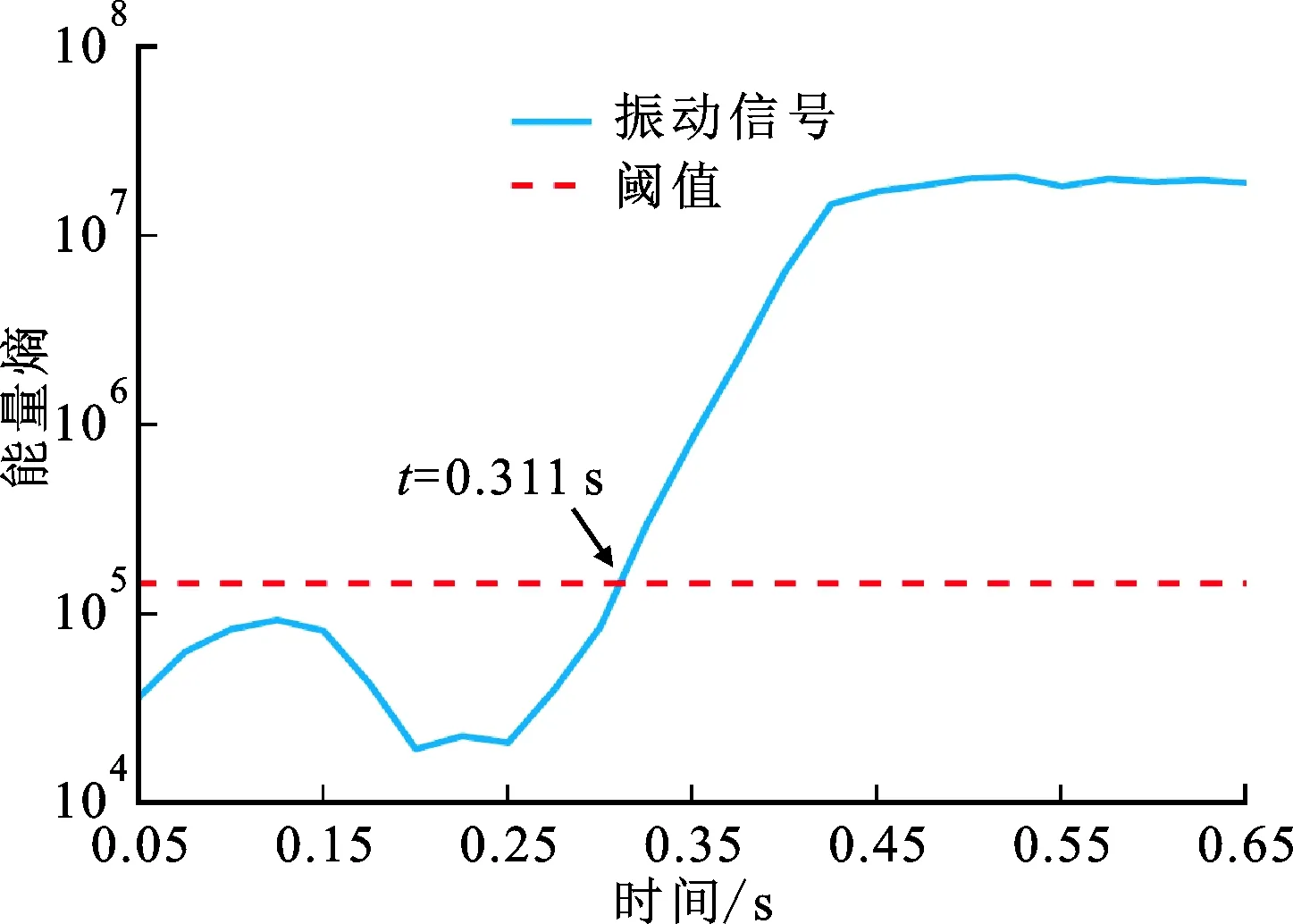
(b)能量熵曲线

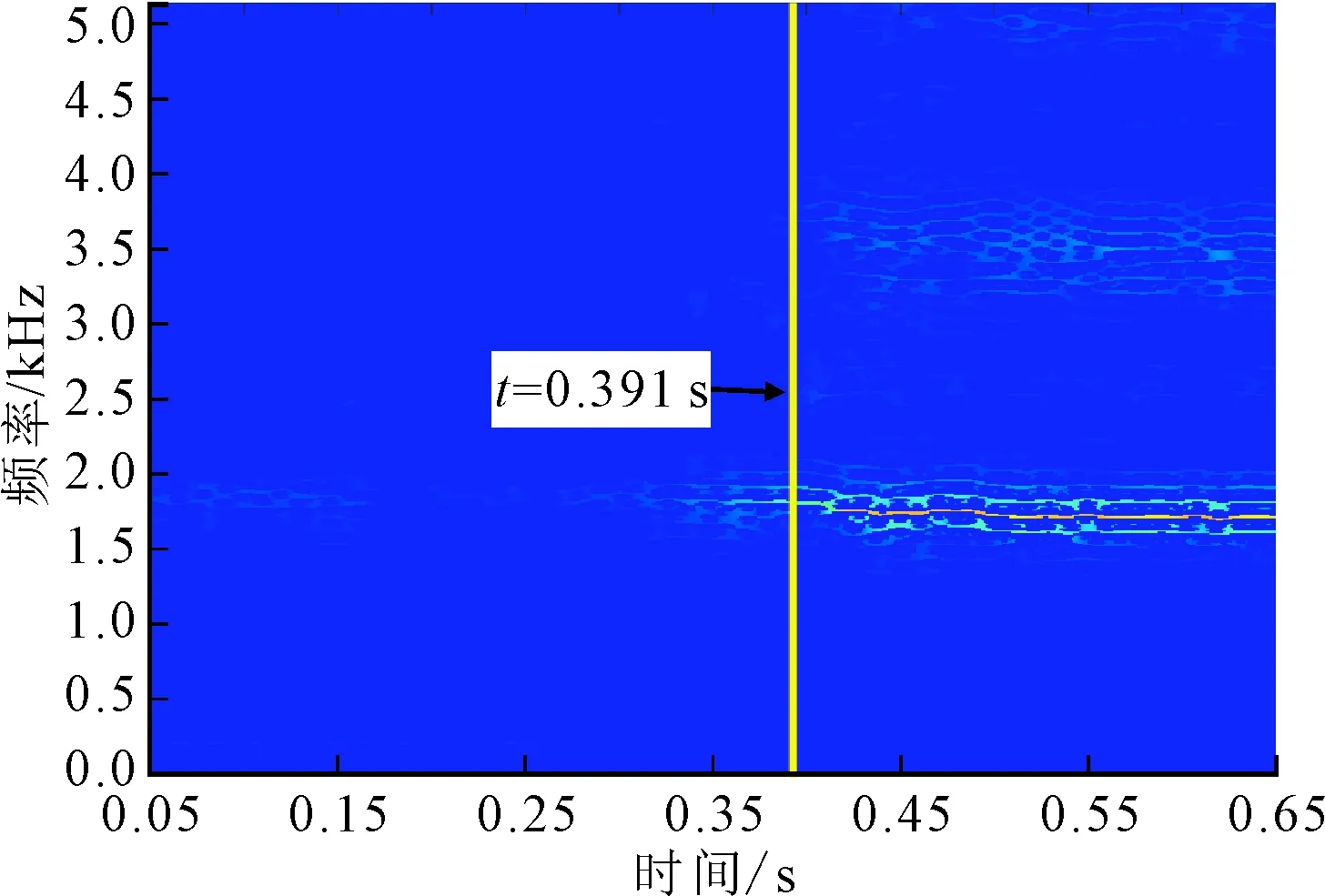
(c)SST谱图4 实验2的颤振监测结果

实验3为进一步验证所提方法的适用性和有效性,采用刀具II和铝合金AL7075工件进行了更多的加工实验。当主轴转速为3 000 r/min、进给速率为6.0 mm/s时,图5给出了实验3的颤振监测结果。从图5b可以看出,信号能量熵在开始阶段数值较小,随后增长速度明显加快,在t=0.162 s时能量熵超过阈值,此时辨识出了颤振。从图5a的时域波形可以看到,在约t=0.212 s后,振动信号幅值才有明显的增长。同时,观察图5c的SST谱发现,相对明显的颤振频率出现在t=0.216 s时,因此所提颤振监测算法能在颤振充分发展之前将其有效检测出来。

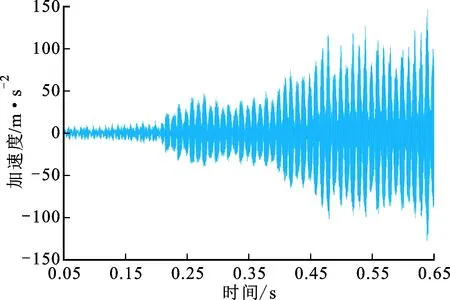
(a)振动时域波形

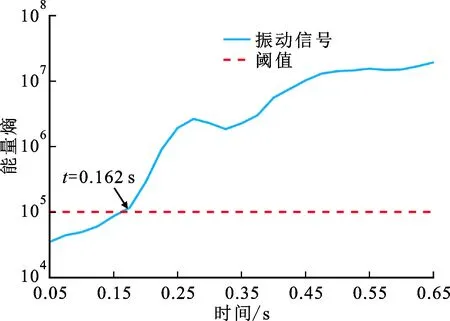
(b)能量熵曲线

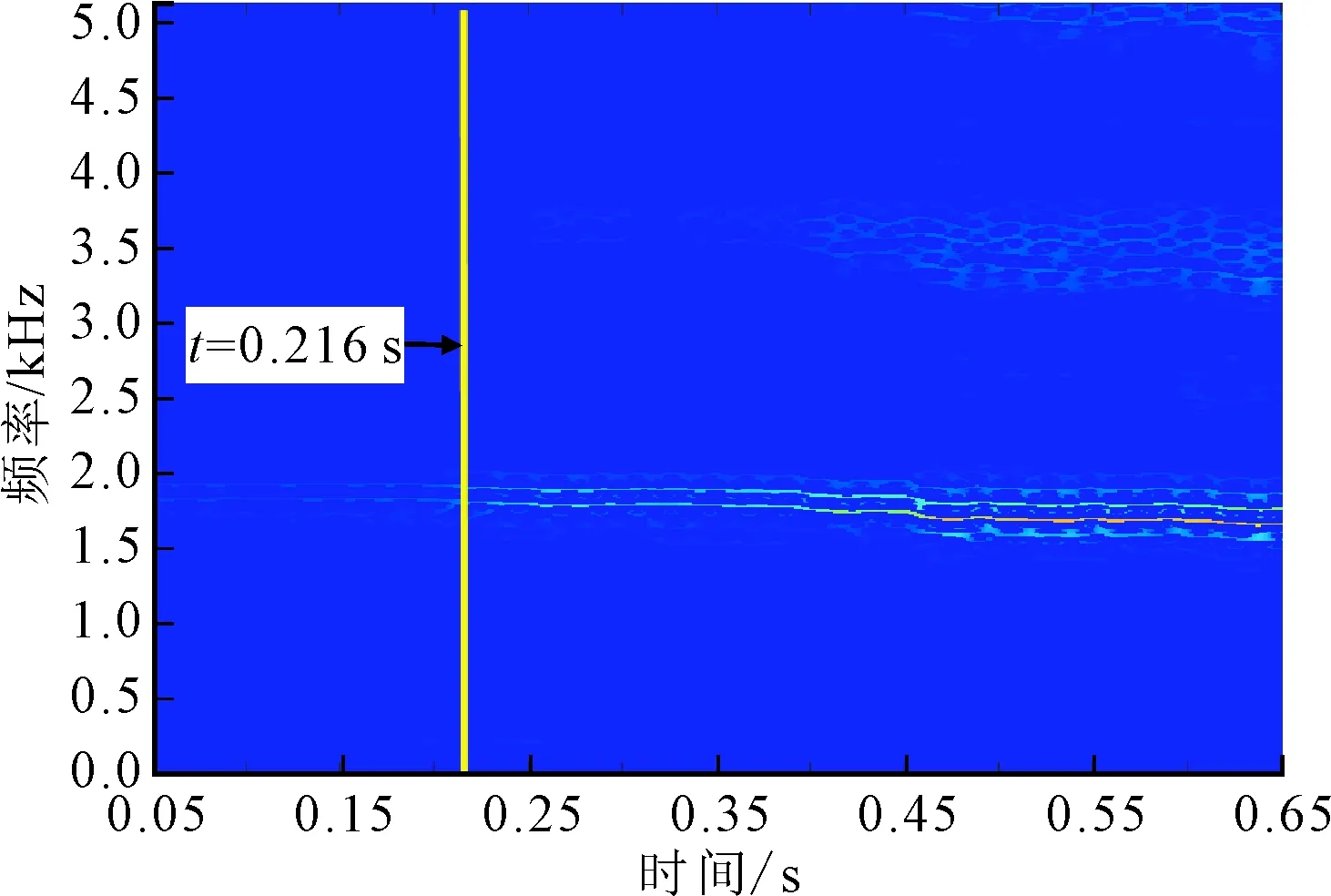
(c)SST谱图5 实验3的颤振监测结果

实验4采用刀具II加工铝合金AL7075工件,当主轴转速为4 500 r/min、进给速率为3.2 mm/s时,图6给出了振动信号、能量熵曲线以及SST谱图。从图6b来看:能量熵在开始阶段相对较小且保持平稳,在t=0.212 s后增长明显加快;当t=0.257 s时,能量熵超过阈值,说明算法识别出了颤振,而从图6a来看,在t=0.271 s左右时振动幅值才显著增加。同时,由图6c的SST谱可以发现,在t=0.279 s时刻时频谱才出现相对明显的颤振频率。上述不同参数下的实验结果表明:本文所提监测算法能够在颤振萌芽阶段有效地将其识别出来,并适用于不同加工条件下的机器人钻削加工。

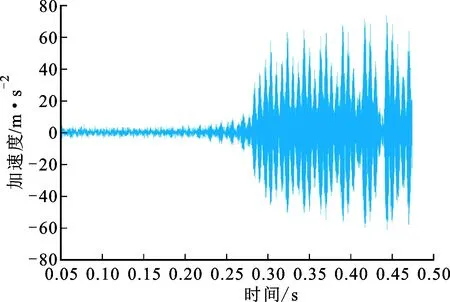
(a)振动时域波形

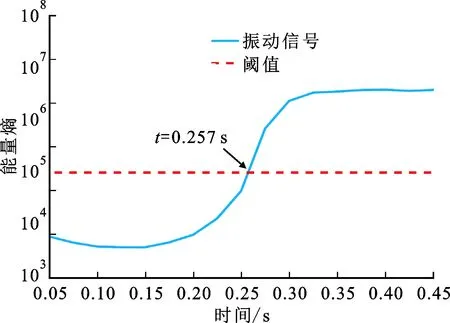
(b)能量熵曲线

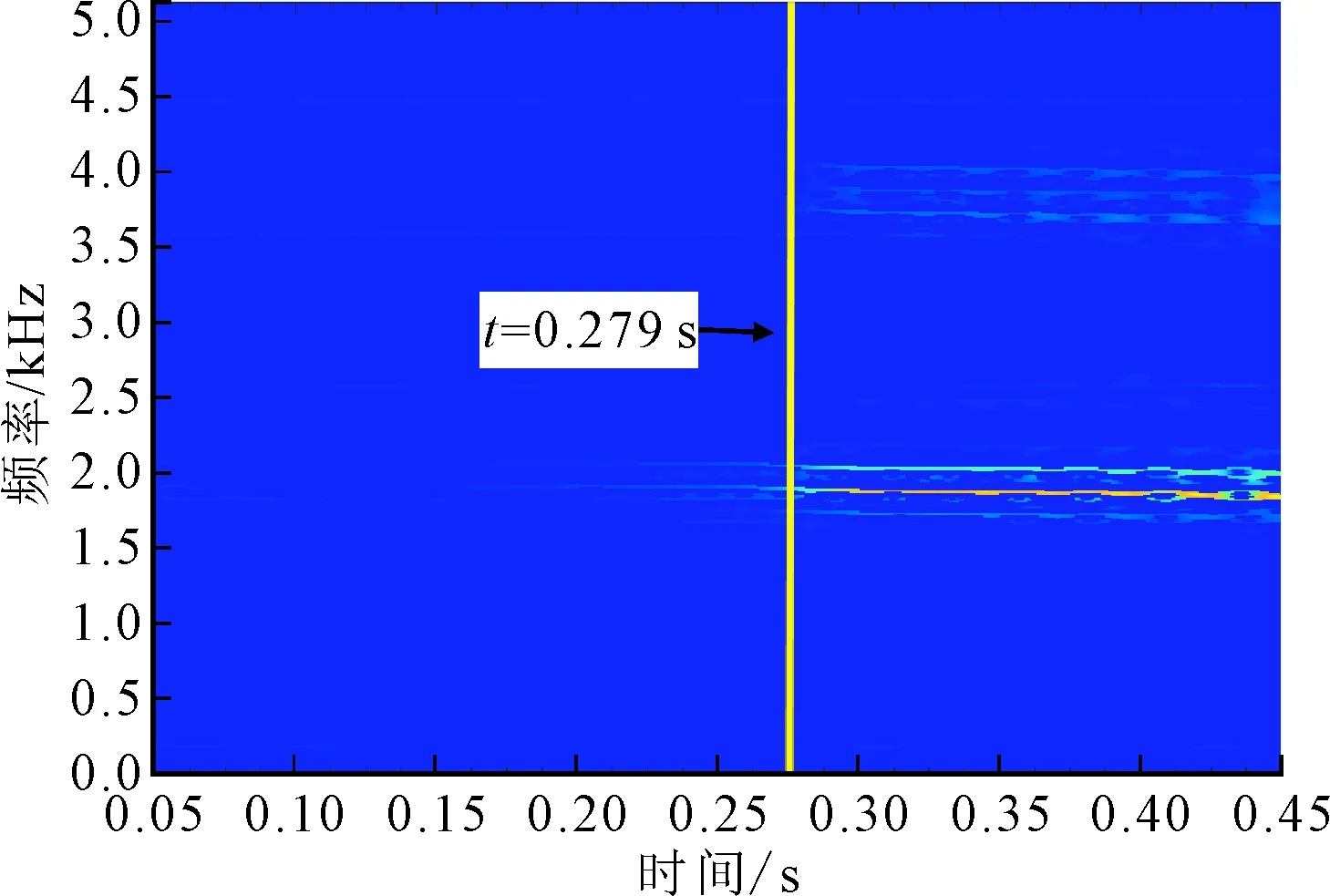
(c)SST谱图6 实验4的颤振监测结果

实验4中加工孔的表面质量如图7a所示。为对比机器人加工过程中有、无颤振时的加工质量,采用与实验4相同的刀具及工件材料,在主轴转速为1 800 r/min、进给速率为5.7 mm/s时得到一组稳定钻孔的工件加工表面,如图7b所示。对比图7a、7b可以发现,稳定钻削时加工孔的表面十分光滑,而当加工系统发生颤振时,刀具在工件表面留下了明显的振动纹路。

(b)无颤振

(a)有颤振

3 结 论

提出了一种基于同步压缩变换和能量熵的机器人加工颤振监测方法。利用加速度传感器测量加工系统振动信号,通过同步压缩短时傅里叶变换获取高分辨率的时频谱,再将振动信号分为有限个频带,重构得到各频带对应的时域子信号。针对颤振发生时振动信号时频及能量分布变化的特点,采用能量熵作为颤振监测的特征量,通过实时计算系统的能量熵进行颤振的在线监测。为验证本文方法的有效性,设计并开展了不同加工条件下的机器人加工实验。研究结果表明:本文所提颤振监测方法能够在机器人加工颤振发生早期有效地将其检测出来,并适用于不同加工条件。此外,计算一次能量熵大约需要20 ms的时间,基本满足颤振在线监测的实时性要求。