谐波齿轮传动双圆弧齿形双向共轭设计方法
2019-08-22姜歌东王爽梅雪松张弦张豪
姜歌东,王爽,梅雪松,张弦,张豪
(1.西安交通大学陕西省智能机器人重点实验室,710049,西安; 2.西安交通大学机械制造系统工程国家重点实验室,710049,西安; 3.西安交通大学机械工程学院,710049,西安)
谐波齿轮传动是20世纪50年代诞生的一种传动技术。根据谐波齿轮传动原理构建的传动装置(即谐波减速器)具有传动比大、回转精度高、体积小等特点,适用于对精密传动有较高要求的场合,被广泛应用在机器人、航空航天、精密仪器等领域。
在谐波齿轮传动中,齿形会对传动啮合性能有很大的影响。最初Musser发明谐波传动使用的是直线齿形[1],后来由工艺性较好的渐开线齿形代替,逐渐发展到更符合啮合原理的新齿形[2];日本学者Ishikawa提出通过齿条近似法得到基本实现连续接触的“S齿形”[3];辛洪兵在圆弧齿廓的基础上提出柔轮和刚轮双圆弧基本齿廓设计方法[4]。目前国内所研究的双圆弧齿形如图1所示,其工作齿廓由两段圆弧段构成,中间通过公切线段平滑连接。

图1 双圆弧齿形及啮合运动


图2 双圆弧共轭齿廓

(a)双共轭(b)二次共轭(c)交叉图3 共轭齿廓分布情况


本文根据双圆弧齿形的分段特点,提出了一种将柔轮和刚轮的齿形进行联合共轭计算的双向共轭设计方法,该方法解决了单向共轭法存在的刚轮凸圆弧段共轭齿廓不确定问题,同时减少所需的设计变量,为谐波齿轮传动双圆弧齿形设计提供了一种新的思路。
1 双向共轭齿形设计方法
本文提出的双向共轭法在进行双圆弧齿形设计时的流程如图4所示。

图4 双向共轭法设计流程
1.1 谐波传动坐标系与几何关系
谐波传动平面啮合计算时满足以下假设[14]:①原始曲线不伸长;②柔轮变形后的各特征曲线均视为原始曲线的等距曲线;③柔轮轮齿不变形并沿原始曲线均布;④将波发生器视为刚体。
建立波发生器坐标系{OXY},柔轮轮齿坐标系{o1x1y1},刚轮坐标系{o2x2y2},如图5所示。此时,变形前的柔轮中性层半径rm为

图5 谐波传动各坐标系
(1)
式中:Db为柔性轴承外径;δf为柔轮齿根处壁厚。变形后的原始曲线的矢径为
ρ(φ)=rm+ω(φ)
(2)
式中:φ为位置角参数,即与波发生器长轴的夹角;ω为原始曲线径向位移,由波发生器外廓线确定。根据柔轮变形[14]可以得到

(3)
式中:υ为中性层周向位移;μ为中性层法向转角。根据柔轮中性层曲线不伸长假设和几何关系可知
(4)
式中:φ1为柔轮变形端转角;φ2为刚轮转角;z1、z2分别为柔轮和刚轮的齿数;γ为柔轮与刚轮的转角差;φ为柔轮坐标系与刚轮坐标系的y轴夹角。
1.2 通过参数预设确定柔轮凸圆弧齿廓

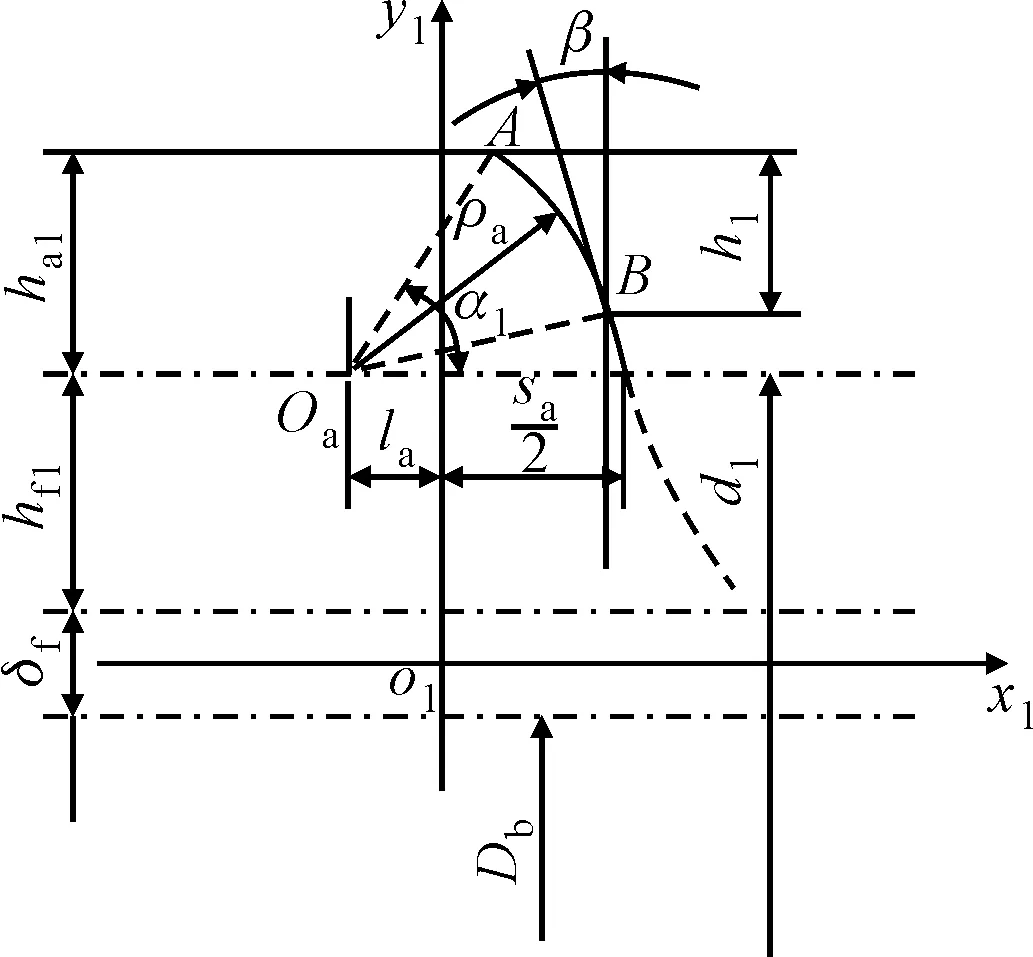
图6 柔轮凸圆弧齿廓
完成参数预设后,开始计算柔轮凸圆弧齿廓参数。谐波减速器柔轮内壁与柔性轴承配合,其内径直接选用标准柔性轴承的外径,柔轮的节圆直径为
d1=Db+2δf+2hf1
(5)
节圆齿厚为
Sa=πd1/[(1+K)z1]
(6)
柔轮凸圆弧半径为
ρa=(ha1-hl)/sinβ
(7)
凸圆弧圆心在节圆上,其到对称轴的距离为
la=ρa/cosβ-Sa/2
(8)
在柔轮轮齿坐标系{o1x1y1}中,以到齿顶点A的弧长s为参数将柔轮凸圆弧齿廓坐标表示为
(9)
式中:参数s的范围为[0,ρa(α1-β)];α1为齿顶A的压力角;(xOa,yOa)为柔轮凸圆弧圆心坐标。
1.3 求解刚轮齿形
根据几何关系,将柔轮齿廓点转换到刚轮坐标系下
(10)
将齿廓坐标代入包络方程[14]
(11)



图7 刚轮双圆弧齿形
1.4 求解柔轮齿形
在刚轮坐标系{o2x2y2}中,刚轮凸圆弧齿廓坐标以到齿顶点V的弧长s为参数表示为
(12)
式中:参数s的范围为[0,ρp(α2-β2)];α2为齿顶的压力角;(xp,yp)为刚轮凸圆弧圆心坐标。同理,将刚轮齿廓点转换到柔轮坐标系下

(13)



图8 柔轮双圆弧齿形
2 齿形设计计算实例
2.1 齿形计算结果

为了说明双向共轭法与单向共轭法的区别,这里选用相同的参数分别计算,参数取值见表1,单向共轭法需要先确定柔轮双圆弧齿形,而双向共轭法,简称双向法,不需要设置凹圆弧参数,减少所需设计参数。

表1 柔轮齿形设计参数取值
齿形参数计算结果见表2,其中各参数如图7、8所示。表2中柔轮齿形参数在单向法中均通过经验方法选取[15],而双向法中是通过共轭和拟合得到的。两种方法的刚轮齿廓基本相同,都是由柔轮凸圆弧段的共轭齿廓确定。在啮合最深处时啮合状态如图9所示。单向法得到的结果属于图3b的情况,齿根圆弧段没有参与啮合;而双向共轭法中柔轮与刚轮齿廓在整个工作齿高内都有较好的接触,而且柔轮齿根部更厚,有利于强度的提高。

表2 齿形参数计算结果 mm


(a)双向共轭法(b)单向共轭法
2.2 双圆弧轮齿啮合侧隙分析
侧隙是评价谐波传动啮合状态的定量指标,可以用于判断轮齿干涉,分析齿间载荷分布[16]。本文所研究的侧隙定义为正常装配下、空载时柔轮齿廓与刚轮齿廓的周向间隙[14]。
两种方法的齿形计算结果在整个工作齿廓段的侧隙分布如图10所示。从图10中可以看出,在整个啮合过程中侧隙大于0,说明没有发生齿廓干涉,两种设计方法的结果都是合理的。以侧隙小于0.003 mm作为可能产生接触啮合条件[14],双向法设计结果在参与啮合的齿廓长度最大为0.53 mm,而单向法设计结果中参与啮合的齿廓长度最长为0.22 mm,说明双向法设计齿廓接触段更长。

(a)双向共轭法

(b)单向共轭法图10 两种方法齿形计算结果的侧隙分布


图11 最小侧隙点位置
单一轮齿在啮合时有多个齿廓点同时发生接触被称为多点啮合现象。多点啮合可以增大齿廓接触


图12 不同齿廓段的最小侧隙分布
2.3 平面有限元接触分析
为了验证侧隙啮合分析结果,在有限元软件Ansys中建立谐波传动平面有限元模型。将波发生器简化为凸轮的等距曲线,刚轮和柔轮都简化为平面齿圈[17]。在柔轮齿廓和刚轮齿廓,柔轮与波发生器分别建立接触对。将刚轮和波发生器的位置固定,负载通过扭矩施加在柔轮内壁上。通过有限元接触仿真得到负载下齿廓的啮合情况。在40 N·m负载下柔轮齿廓上的接触应力如图13所示。

(a)双向共轭法

(b)单向共轭法图13 两种方法的齿廓接触应力
图13中接触应力为0,表示没有发生啮合接触,其他部分存在接触应力,说明该处齿廓点产生了啮合作用。从图13中可以看出,双向共轭法结果的接触齿廓较长,并且有轮齿存在两段接触齿廓,验证了多点啮合现象。单向共轭法结果的接触点均在凸圆弧段。有限元接触分析的结果与侧隙分析结果一致。对比最大接触应力,双向共轭法结果为44.175 MPa,单向共轭法结果为53.862 MPa,说明通过增大接触面来减小齿面接触应力,从而减小齿面磨损是可行的。
3 结 论
本文通过平面啮合理论对谐波齿轮传动的双圆弧齿形设计方法进行了研究,得到以下结论。
(1)本文提出双向共轭设计方法,用于谐波齿轮传动的双圆弧齿形设计。与常用的单向共轭法相比,双向共轭法增加了从刚轮齿廓共轭计算柔轮齿廓的环节,解决了单向共轭法设计时刚轮凸圆弧段共轭齿廓不确定问题,并且减少了所需的设计参数。
(2)啮合侧隙分析结果表明,与单向共轭法相比,双向共轭法设计的双圆弧齿形参与啮合的齿廓段更长、三段齿廓都参与啮合,能够实现多点啮合,有利于减小啮合力、降低齿面磨损。
(3)平面有限元接触分析表明,与单向共轭法相比,双向共轭法设计的双圆弧齿形在负载下具有更大的齿廓接触面积和更小的齿面接触应力,有利于降低齿面磨损,进一步验证了侧隙分析的结论。
(4)本文提出的双向共轭设计方法不仅提升谐波齿轮传动双圆弧齿形设计效果,也为其他类型分段齿形设计提供了一种可以借鉴的设计思路。
