Analytical modeling for rapid design of bistable buckled beams

Wenzhong Yan, Yunchen Yu, Ankur Mehta

Samueli School of Engineering, University of California, Los Angeles, CA 90095, USA

Keywords:Bistable buckled beam Theoretical model Snap-through characteristics Off-center actuation Analytical expression Rapid design

A B S T R A C T Double-clamped bistable buckled beams demonstrate great versatility in various fields such as robotics, energy harvesting, and microelectromechanical system (MEMS). However, their design often requires time-consuming and expensive computations. In this work, we present a method to easily and rapidly design bistable buckled beams subjected to a transverse point force. Based on the Euler-Bernoulli beam theory, we establish a theoretical model of bistable buckled beams to characterize their snapthrough properties. This model is verified against the results from a finite element analysis (FEA) model, with maximum discrepancy less than 7%. By analyzing and simplifying our theoretical model, we derive explicit analytical expressions for critical behavioral values on the force-displacement curve of the beam. These behavioral values include critical force,critical displacement, and travel, which are generally sufficient for characterizing the snapthrough properties of a bistable buckled beam. Based on these analytical formulas, we investigate the influence of a bistable buckled beam's key design parameters, including its actuation position and precompression, on its critical behavioral values, with our results validated by FEA simulations. Our analytical method enables fast and computationally inexpensive design of bistable buckled beams and can guide the design of complicated systems that incorporate bistable mechanisms.

1 Introduction

Bistable mechanisms, featuring their two stable equilibrium states, have been under investigation for a long time. These mechanisms are ideal as switches because power is only required for switching them from one equilibrium state to the other but not for maintaining a current state. Meanwhile, their rapid and large-stroke transition between the two stable states during snap-through motions makes them great candidates for actuators. Thanks to these advantages, bistable structures are extensively harnessed in various engineering domains, such as microelectromechanical system (MEMS) [1-3], robotics [4-6], energy harvesting [7-9], actuators [10, 11], origami technology[12, 13], signal propagation [14], and deployment mechanisms[15]. In addition, bistable mechanisms possess high reliability and high structural simplicity and consume relatively little power when incorporated into mechanical systems, which are potentially desirable for aerospace applications, e.g. energy absorbing [16] when aerospace devices are subjected to foundation excitation [17, 18] or sudden unbalance [19]. These desirable properties suggest more dedicated efforts be put into investigating these mechanisms.

Among various types of bistable mechanisms, doubleclamped bistable buckled beams (Fig. 1) have drawn the attention of many researchers, thanks to their remarkable manufacturability and versatility [10, 20, 21]. Early on, Vangbo [22] studied the nonlinear behavior of bistable buckled beams under center actuation with a Lagrangian approach under geometric constraints and was able to express both the bending and the compression energy associated with the snap-through motion with buckling mode shapes of the bistable beam. This method was verified by Saif [3], who also extended the method to tunable micromechanical bistable systems. Qiu et al. [23] then explored the feasibility of this method on double curved beams (i.e. two centrally-clamped parallel beams). Moreover, an analytical expression of the relationship between the force applied at the beam's center and the corresponding displacement was derived, making the characterization and design of the bistable mechanism easier. Nevertheless, most efforts were put into the modeling of bistable buckled beams under center actuation, while only a few works [24, 25] have tackled the modeling of bistable beams under off-center actuation. Still, off-center actuation possesses unique behavioral properties that make it suitable for many applications. For example, compared to center actuation, off-center actuation usually requires a smaller actuation force but features a longer actuation stroke [26, 27]. In addition, off-center actuation schemes highly pertain to applications with geometric constraints at the mid-span position of the beam [28]. In this paper, we extend the work of Vangbo [22] to bistable buckled beams under off-center actuation to facilitate their design process based on theoretical analysis.

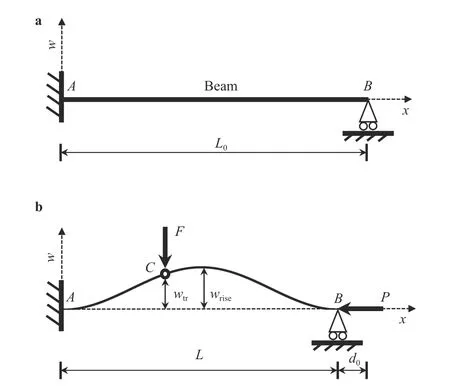
Fig. 1. Clamped-clamped bistable buckled beam. a Non-loaded straight beam, b beam in its buckled configuration with an actuating force applied at the location C

The design of bistable mechanisms largely relies on their snap-through characteristics. Typically, the snap-through characteristics of a bistable structure can be primarily represented by three behavioral values, i.e. the critical forceand the critical displacementat the bistable mechanism's switching point,as well as the travelat the stable equilibrium point, as shown in the force-displacement curve in Fig. 2. These critical behavioral values are determined by design parameters, i.e. the geometry (including the length, width and thickness of the slender beam), precompression [22], actuation position [25, 29], and boundary conditions [26, 30]. Due to the complicated coupling between snap-through characteristics and design parameters, it is often challenging to design a bistable structure efficiently. So far, lots of efforts aiming at efficiently designing bistable mechanisms have been made. Camescasse et al. [25, 31] investigated the influence of the actuation position on the response of a precompressed beam to actuation force both numerically and experimentally, based on the elastica approach. A semi-analytical method for analyzing bistable arches, which involves numerically extracting critical points from bistable arches' force-displacement curves, was also presented in previous works [32, 33].Due to the intrinsically strong nonlinearity of bistable mechanisms, existing models are rather complicated and usually involve differential equations that could only be solved semi-analytically or even numerically. Recently, Bruch et al. [34] developed a fast, model-based method for centrally actuated bistable buckled beams, which, however, requires heavy computation with finite element analysis (FEA) methods. Thus, rapidly and efficiently designing bistable mechanisms, especially those under off-center actuation, remains a huge challenge.

In this work, we develop a method for the rapid design of double-clamped bistable buckled beams. Similar to Vangbo's work [22], the Lagrangian approach is adopted in the theoretical model to determine the contribution of each buckling mode shape under geometric constraints. Through analyzing and simplifying the theoretical model, explicit analytical expressions of the critical force, critical displacement, and travel are obtained.Moreover, based on the presented model, a detailed analysis of the influence of design parameters, including actuation position and precompression, on the snap-through characteristics of the beam is presented and validated by an FEA model. Thus, given a set of design parameters, our analytical formulas can output the critical behavioral values in real-time, consistent with results from FEA simulations which usually take hours on the same machine. Specifically, the contributions of this work include:

(1) a generic model of double-clamped bistable buckled beams under center and off-center point force actuation based on the Euler-Bernoulli beam theory;

(2) analytical formulas of a bistable beam's critical behavioral values that characterize its snap-through properties, which give rise to a rapid and computationally efficient design method of double-clamped bistable buckled beams;

(3) an analysis of the influence of design parameters on the snap-through characteristics of bistable buckled beams, with results validated by FEA simulations.

The structure of the paper is as follows: the bistable system is described in Sect. 2; the theoretical model of bistable buckled beams is presented and simplified in Sect. 3; the explicit analytical expressions of the beam's snap-through characteristics are derived in Sect. 4; our main results and discussions are showcased in Sect. 5, followed by conclusions and future work in Sect. 6.

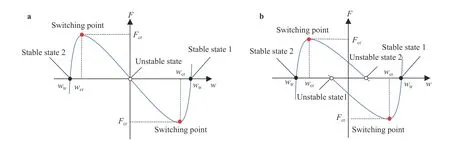
Fig. 2. Characteristic force-displacement curve of bistable buckled beams. a Under center actuation, b under off-center actuation

2 Description of the system

Here we consider a clamped-clamped and initially straight elastic beam, as shown in Fig. 1. The original length, width,thickness, and Young's modulus of the beam are denoted as,,, and, respectively. Under a compressive axial load, one of the beam's terminals moves towards the other, resulting in a first-mode buckling shape with initial rise(i.e. the initial displacement of the beam's mid-span). The distance between the two terminals of the beam after buckling, what we refer to as the span, is denoted as; the difference between the original length and the span is denoted as(i.e.).Moreover,the cross-sectionalarea of the beam■and the se■cond moment are denoted asand, respectively.

The system's two-dimensional reference frame is chosen such that the x-axis coincides with the line connecting the two ends of the beam after it is axially compressed, while the-axis is set perpendicular to the x-axis at one end of the beam, as shown in Fig. 1. A point forcein thedirection is applied vertically to the buckled beam at a selected location C. The ratiois the parameter that indicates the position at whichis applied to the beam.

3 Modeling and analysis

In this section, a theoretical model of bistable buckled beams is derived and subsequently simplified. This model allows for characterizing the snap-through properties of a bistable buckled beam and enables the derivation of analytical expressions of the beam's important snap-through characteristics.

3.1 Theoretical model

According to Euler's buckling model of a double-clamped slender beam, when the axially compressed beam is undisturbed (i.e.), its behavior can be described with the following differential equation

The eigenvalues of this homogeneous Strum-Liouville problem can be denoted in form of, and these eigenvalues satisfy the equation

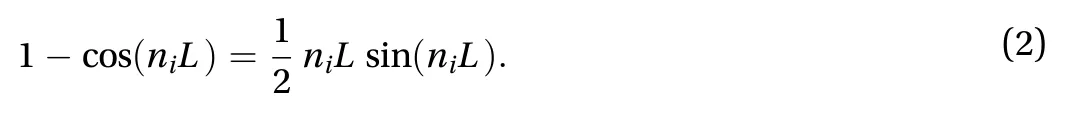
The eigenvalues give rise to a series of nontrivial eigenfunctions of Eq. (2)

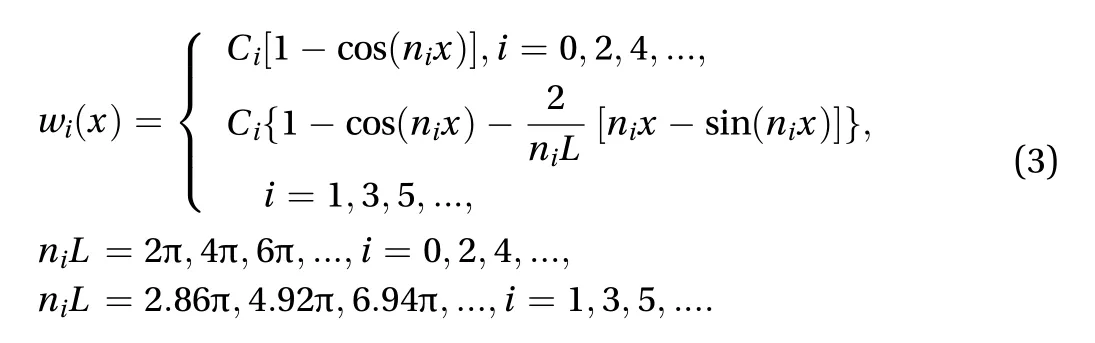
where the set of amplitudesminimizes the energy of the system under the constraint of the beam's current length,[22].refers to the contraction from the axial loadand is given as. Thus, we have the following equation

where the three terms refer to the bending energy of the beam,the potential energy of the force, and the compression energy,respectively [22]. In Vangbo's work [22], the parameterin the second energy term is always set to 0.5 as the force is applied at the beam's center; in this work, however, we allowto vary in order to account for off-center actuation.

Therefore, we solve for thethat minimizein Eq. (7) and conform to the constraint specified by Eq. (6). We introduce a Lagrange multiplierin order to find the equilibrium state of the beam under a force. We consider

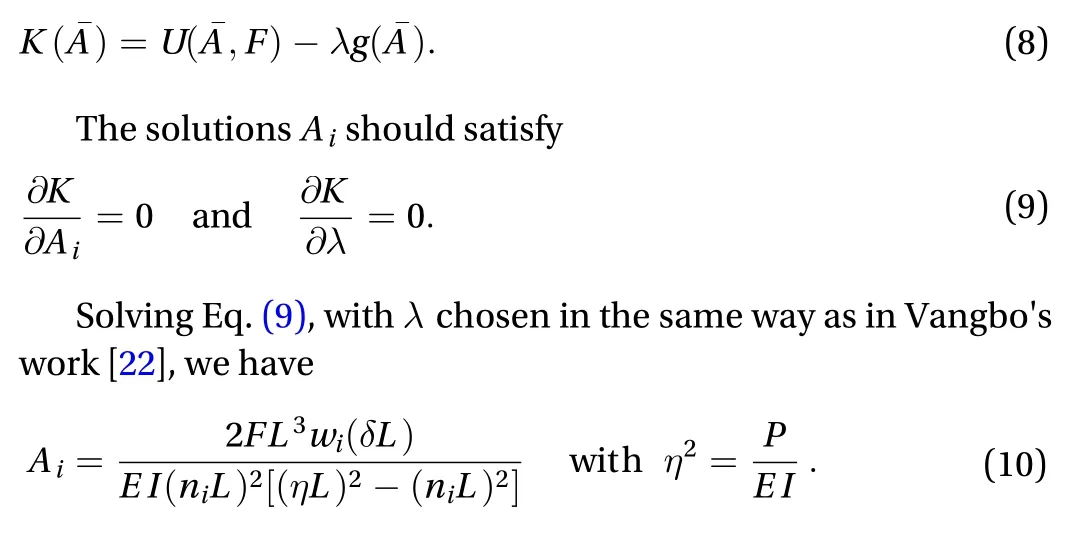
Combining Eq. (10) and the constraint given by Eq. (6), we can determine the magnitude ofwhen given a value of the parameter

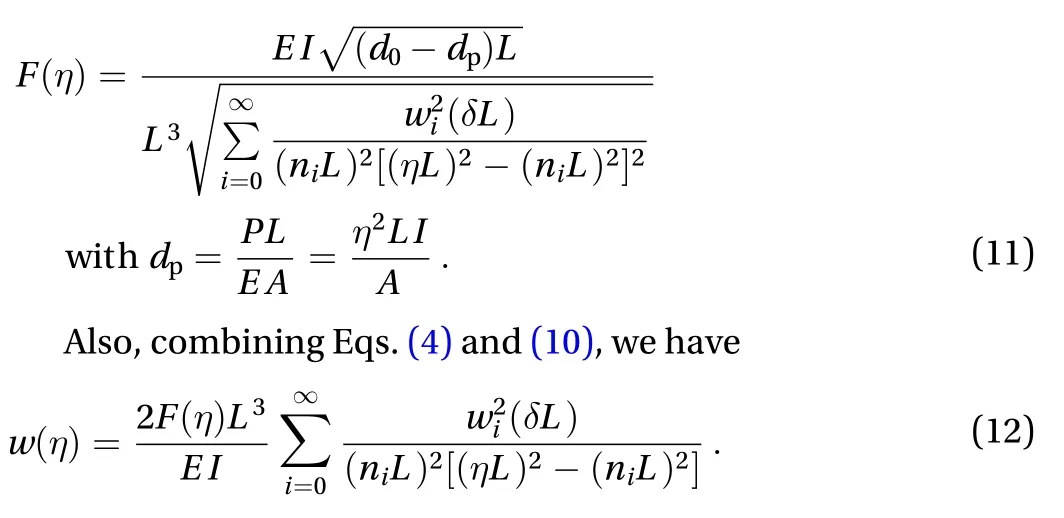
Equations (10)-(12) characterize the connections among the actuating force, the beam's displacement, and the axial load() applied to the beam from side walls. Importantly,the obtained force-displacement curve can be used to characterize the mechanical properties of the bistable buckled beam.

3.2 Reduced model

As largely mentioned in Refs. [23, 24], the first two modes of buckling,and, have predominant contribution in the beam's displacementin both center and off-center actuation scenarios [24]. Thus, we can make the approximation thatand write

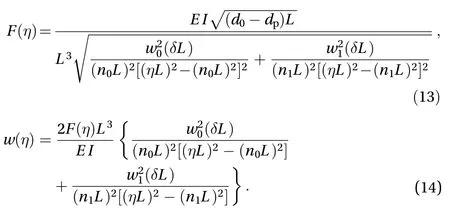
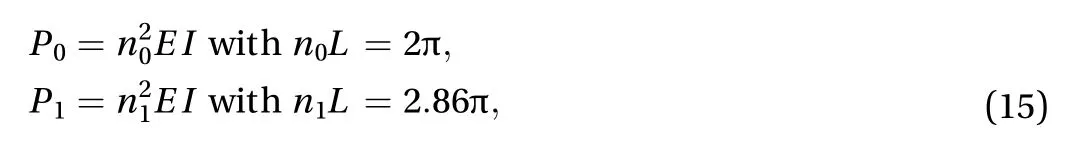
4 Analytical expressions of the snap-through characteristics

Generally, the three critical behavioral values,,, andon the force-displacement curve are sufficient for characterizing a bistable buckled beam and facilitating its design. Given the significance of these behavioral values, it is worthwhile to develop explicit analytical expressions for each of them.

4.1 Critical force

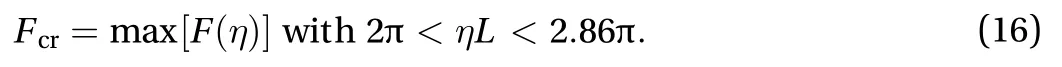
To simplifyEq.(16), we take advantage of the fact that the Therefore, we have

It can be observed from Eqs. (18) and (19) that(denoted as) and thusare only dependent on the parameter. In other words, we can denoteon

To obtain an analytical form of, we varyfrom 0.15 to 0.5,the scope of this parameter within our consideration (note that by symmetry, we only need to consider one half of the beam),and calculate the corresponding values of. We then apply curve-fitting to obtain an analytical relationship betweenand.as a function ofis visualized in Fig. 3 and presented in Eq. (21) with the error of fitting less than 7%.is chosen as a degree-4 polynomial to ensure relatively high accuracy and acceptable complexity of the model. Note that this curve-fitting can be reperformed to improve the accuracy of the final result or to reduce the complexity of the model.

The analytical expression of the critical forceat a precompressed beam's switching point can be written as Eq. (21). Note that the minimal critical force is achieved whereis equal to 0.37 (or 0.63)

4.2 Critical displacement

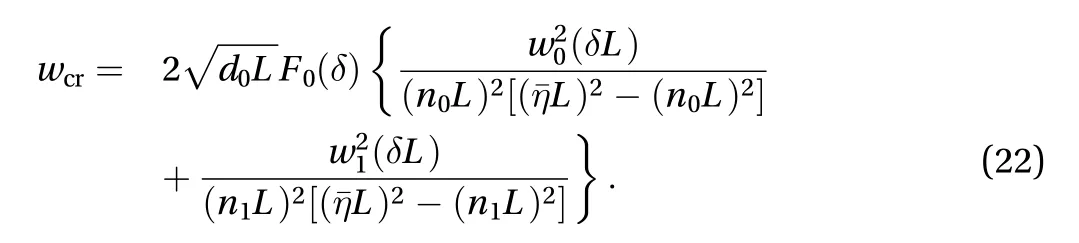
Since we have shown that ? onlydepends on, we can conwith, some function of. To obtain an analytical form of,we vary the parameterfrom 0.15 to 0.5 and calculate the corresponding values of.as a function ofis displayed in Fig. 3 and its analytical form is shown in Eq. (23) after some change of variables. The analytical expression ofis written as follows

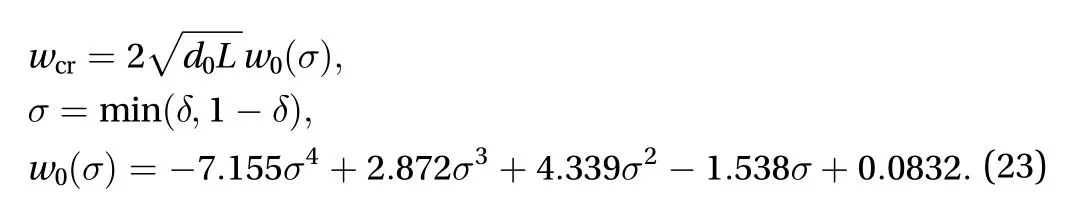
Again, the curve-fitting can be reperformed for alternative analytical expressions of. Moreover, it is important to note that the critical displacement is primarily dependent on,,and, a result consistent with that of Bruch et al. [35] but obtained with a different method.

4.3 Travel

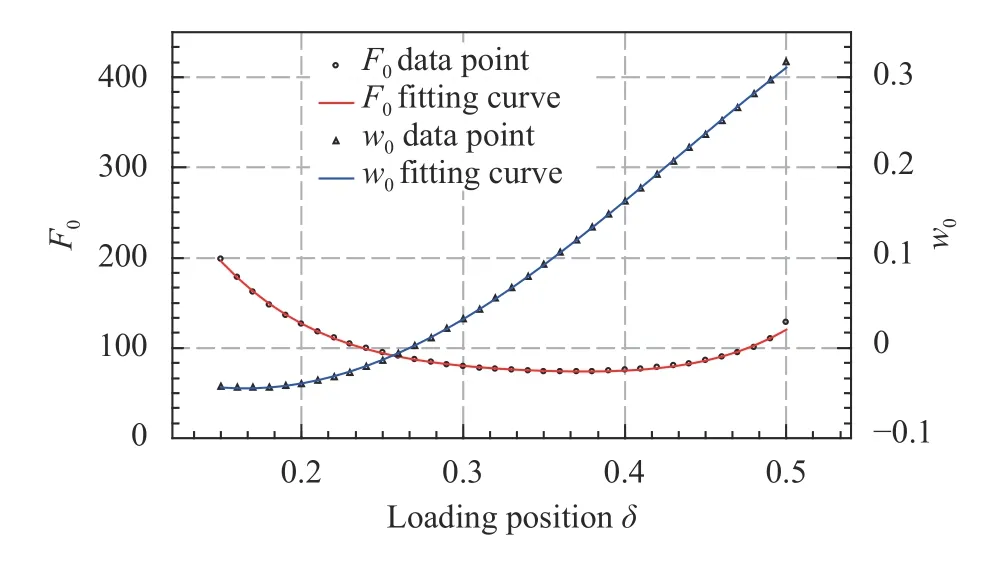
Fig. 3. Curve fitting of and

The initial shape of an axially compressed beam can be approximated using the cosine curve featured in the expression of. Thus, we haveby definition of the travel, whereis the initial rise of the beam's midpoint,determined by the degree of compression. Considering Eq. (5),since we have shown that, we can ignore the termand approximatefrom the following relationship

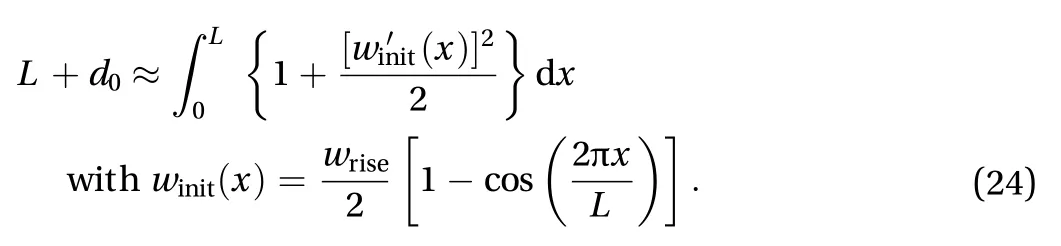
It can be calculated from Eq. (24) that, and so we have

One significant observation from Eqs. (23) and (25) is that the value ofonly depends on the parameter. The key insight is that when designing a precompressed bistable mechanism, the possible constraints on these two behavioral parameters may uniquely determine its optimal actuation position.

5 Results and discussions

In this section, we consider a double-clamped bistable buckled beam with its parameters given in Table 1. All of the parameters above remain unchanged throughout this section unless otherwise stated.

5.1 Model validation

To validate our model, we compare our results, theandcurves for both center and off-center actuation of a bistable buckled beam, with quasi-static force-displacement curves from ABAQUS. The bistable beam was modeled in three dimensions and its geometry was meshed with quadrilateral shell elements (i.e. S4R) that can capture large deformation behaviors. The buckling of the beam was introduced by an initial imperfection in the lateral direction. In our analytical model,Eqs. (13) and (14) combined give rise to thecharacteristic,while the relationshipand Eq. (14) combined yield thecurve.

5.1.1 Center actuation

There is a neat agreement between the actuating forceand the compressive forcecalculated from our model and from the FEA model, with errors bounded within 7% and 6%, respectively.Note that the greatest discrepancy occurs around the switching points, where the critical force is modeled fairly accurately, while the critical displacement from our model is larger than that calculated from the FEA model. This means our model suggests a premature snap-through of the bistable beam.

5.1.2 Off-center actuation

Under an off-center actuation (=), theandcurves of the beam are shown in Fig. 5. In the same manner, the solid black curves represent our analytical model while the red (downward) and blue (upward) circles come from the FEA simulation results.

Contrary to the center actuation, the off-center actuation from the two directions results in two distinct branches in thecurve, as shown in both diagrams. This indicates that the switching of the beam involves a branch jump [24]. Similarly,andare the two stable equilibrium points (,).andboth represent the unstable equilibrium state of the beam (,), approached when the beam is actuated by an off-center force from its two different stable positions.Points b1 and b2 are the switching points of the bistable beam.

The results from our analytical method are consistent with the FEA simulation data. Errors on theandcurves with respect to the FEA results are bounded within 2% and 5%,respectively. The small magnitudes of these errors greatly demonstrate the validity of our model.

What can be the reason for such a crowd close by the pigsty? said theEmperor, who happened just then to step out on the balcony; he rubbed hiseyes, and put on his spectacles. They are the ladies of the court; I must godown and see what they are about! So he pulled up his slippers at the heel,for he had trodden them down.

5.2 Influence of design parameters on snap-through characteristics

To facilitate the rapid design of bistable buckled bistablebeams, we discuss the influence of a bistable beam's key design parameters on its snap-through characteristics, namely its critical force, critical displacement, and travel. These results are also verified by an FEA model.

Table 1 Geometric and material parameters of the beam.

5.2.1 Actuation position

Lastly, when the design parameters of the beam are held constant, the mathematical relationship between the travelandsimply features the cosine function discussed in Sect. 4.3,as shown in Fig. 6(e).

As depicted in the Fig. 6(a, c, e), the,, andcurves generated from our model are also compared with those from the FEA model. In addition, the relative errors are presented in Fig. 6(b, d, f). The relative errors ofandwith respective to the FEA simulation data are both bounded within 4%. The critical displacementcalculated from our model matches excellently with the FEA simulation, even though the relative error is fairly notable when the actuation position largely deviates from the beam's center. Within this range, the relative error ofis less informative and is not shown in Fig 6(d).However, in most applications, the actuation position parameterfalls within the range[24, 28, 35], where the errors ofare bounded within 8%. Therefore, our model can be considered generally feasible and accurate.

5.2.2 Precompression

Fig. 4. Center actuation: FEA results and comparison to our model. a Actuating force vs. displacement. b Compressive force vs. displacement

In order to increase the applicability of the following analysis, we define a parameterthat denotes the precompression rate of a bistable buckled beam. Therefore, using the expressionsand, we derive the relationships amongand the behavioral parameters of a bistable beam. Applying Eqs. (21), (23), and (25), we can obtain the relationships between,, andand the precom■pression rate

These mathematical relationships are demonstrated with a bistable beam with design parameters given in Table 1 and withset to 0.43. As shown in Fig. 7(a, c, e), all of the three values increase as the precompression rate increases, with their increment rates decreasing. Again, as shown in Fig. 7(b, d, f), the errors of our analytical model remain small (less than 9% for bothand), with the exception of the critical displacementwhen the precompression rateis very large. The enlarged error ofwhen the precompression rate is large is due to the violation of the small-deflection hypothesis assumed in our model. The error of, however, is bounded within 15% whenfalls in the range, which indicates that our model still greatly applies to most circumstances [10, 20, 27].

6 Conclusions and future work

We have proposed a mechanism that can easily and efficiently characterize the response of a double-clamped bistable buckled beam to point force actuation. Based on the Euler-Bernoulli beam theory, we have established a theoretical model of bistable buckled beams and their behavior under an actuating force. Since we have extended our simulation to beams under off-center actuation, our model is able to guide the design of this class of bistable buckled beams. Moreover, through validation with an FEA model, we have demonstrated that our proposed model is highly accurate.

Fig. 5. Off-center actuation: FEA results and comparison to our model. a Actuating force vs. displacement. b Compressive force vs. displacement

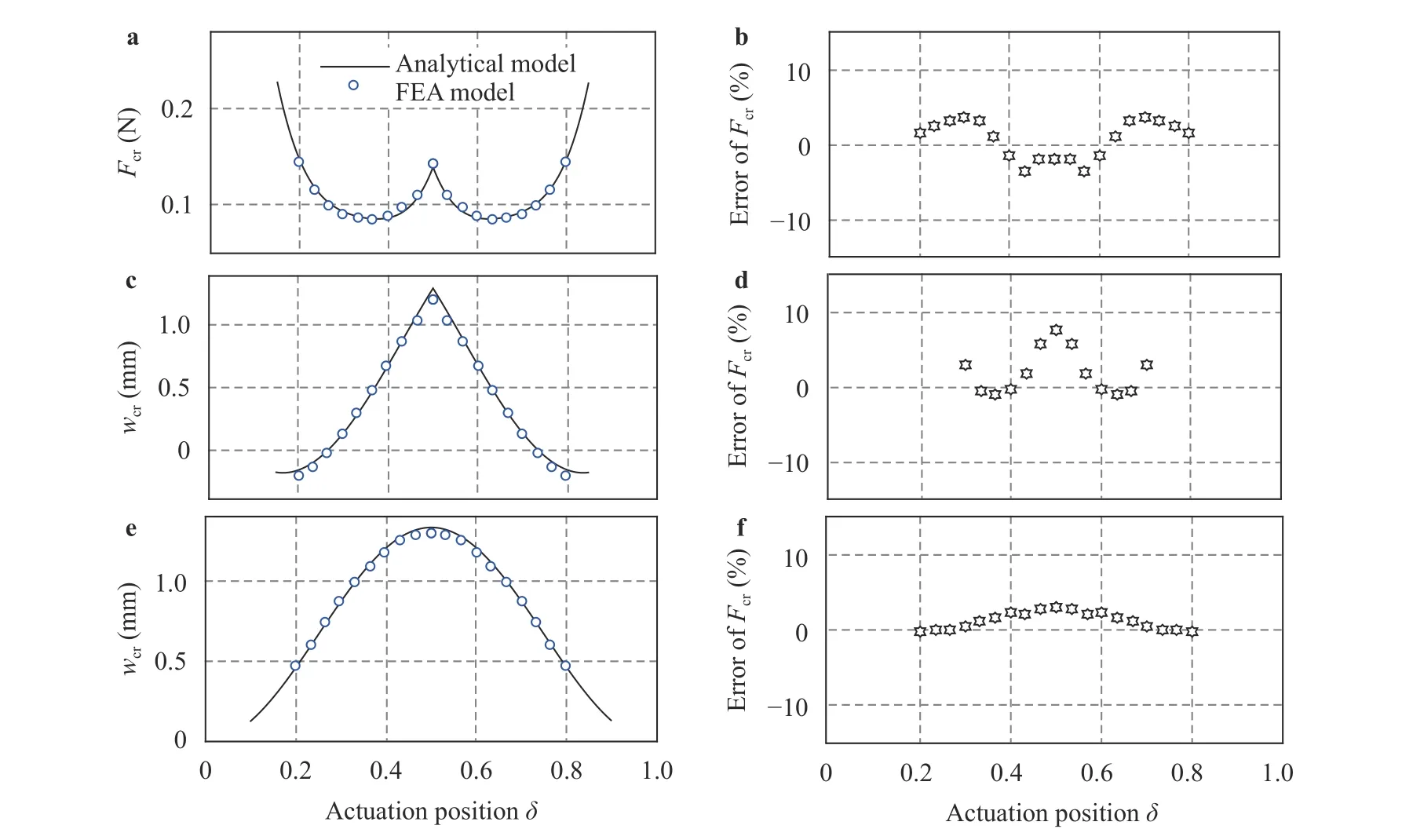
Fig. 6. Effect of actuation position on the critical behavioral values. a Critical force , b error of compared with FEA results, c critical displacement , d error of compared with FEA results. Note that a part of data is not shown here. e Travel , f error of compared with FEA results

Fig. 7. Effect of precompression rate on the critical behavioral values. a Critical force , b error of compared with FEA results, c critical displacement , d error of compared with FEA results, e travel , and f error of compared with FEA results

Our more pragmatic contribution lies in the analytical expressions of the snap-through characteristics of a bistable buckled beam (i.e. its critical force, critical displacement and travel) derived from our theoretical model after some simplifications. These analytical expressions enable rapid computation of critical behavioral parameters of a bistable buckled beam and thus make its design process more efficient. Based on these analytical formulas, we have also investigated the influence of key design parameters of a bistable buckled beam (i.e. its actuation position and precompression) on its snap-through characteristics and verified our conclusions with FEA simulations.

There are several directions in which we can extend our work. One of our most interesting future directions is optimization. For instance, minimizing the total energy consumption of a bistable buckled beam's snap-through motion makes it possible to adopt more compact actuators in an integrated system. In addition, a possible extension of the present work involves building models of bistable beams with other boundary conditions.Most importantly, given the complicated relationships among their design parameters and snap-through characteristics, it is worthwhile to propose a computational pipeline that designs bistable buckled beams with the specified critical behavioral values. In conclusion, we believe that our proposed analytical model is a significant step towards the fast and computationally inexpensive design of bistable buckled beams, which will be easily incorporated into more and more mechanical systems (e.g.shape memory alloys [36, 37] actuated bistable mechanisms).

Acknowledgement

The authors are grateful to Mr. Yuzhen Chen and Mr.Xingquan Guan for their help with the FEA modeling, and to Mr.Weicheng Huang for the fruitful discussions on the modeling of bistable buckled beams. In addition, the authors greatly appreciate the financial support from the National Science Foundation of the United State (Grants 1752575 and 1644579).