Thermal explosion and irreversibility of hydromagnetic reactive couple stress fluid with viscous dissipation and Navier slips

S.O. Salawu*, M.S. Dada, O.J. Fenuga

a Department of Mathematics, Landmark University, Omu-aran, Nigeria b Department of Mathematics, University of Ilorin, Ilorin, Nigeria c Department of Mathematics, University of Lagos, Akoka, Nigeria

Keywords:Thermal criticality Entropy generation Viscous heating Non-Newtonian fluid

A B S T R A C T The study examines the thermal explosion branched-chain and entropy generation as a result of irreversibility of hydromagnetic reactive couple stress liquid with viscous heating and Navier slips.The reactive fluid flow is enhanced by heat dependent pre-exponential factor and axial pressure gradient in a porous wall. The flow equations for the non-Newtonian couple stress fluid model and heat transfer are solved by employing a semi-analytical collocation weighted residual method(CWRM). The efficiency and validity of the obtained results was verified with the existing results.The results reveal that at low hysteresis magnetic and viscous dissipation the irreversibility process is minimized and thermodynamic equilibrium is improved. The results from this study can assist in understanding the relationship between thermal and thermal explosions branched-chain.

Recently, there is an increasing interest in the analysis of thermodynamic processes involving flow of non-Newtonian liquids in a channel. This is because of its usefulness in renewable energy and its application in thermal engineering science such as nuclear reactor, heat exchanger thermal system, energy generation, thermal hydraulics and so on. The needs to improve energy of a system and minimize energy wastage has enhanced interest in non-Newtonian liquids [1]. The liquid with distinctive rheological behaviour that make them more valuable than Newtonian fluids. Among the polar non-Newtonian fluids is the couple stress fluid. Couple stress liquid is a liquid without microstructure but with only one constant material term that accountable for viscous lubricant and couple stress [2, 3]. Flow of hydromagnetic couple stress fluid often accompany with heat transfer in many thermal system. Several machines operate with diverse kinds of lubricant oil under different temperature which often affect the oil viscosity. To avoid or reduce the changes in the lubricant oils as a result of heat, there is need to consider hydromagnetic lubricants as reported by many researchers [4-6].Hyromagnetic lubricants has high thermal conductivity induced by electromagnetic fields which create ohmic heating that help in improving the lubricant viscosity.

Upgrading the performance of machines by monitoring the quantity of the accessible energy in doing work has prompted scientists to study the entropy generation due to irreversibility in a thermal system. Entropy is either unchanged or increases in an adiabatic system. In few of these, analysis of hydromagnetic fluid flow with convective heat transfer using thermodynamic second law was carried out [7, 8]. Flow of peristaltic hydromagnetic energy conversion and entropy production rate in a tube has been examined by Akbar [9]. Unsteady magnetohydrodynamic (MHD) nano-fluid flow and entropy generation in an elongated permeable surface was investigated by Abolbashari et al. [10]. Analysis of entropy generation by MHD viscoelastic flow in a permeable medium past a stretching plate was studied by Baag et al. [11]. The problem was analytically solved by employing Kummer's function. It was reported from the study that Darcy dissipation enhances entropy generation except for fluids with small thermal diffusivity that encourages reversibility process. Salawu et al. [12] reported on entropy generation by irreversibility by variable conductivity Powell-Eyring reactive fluid in non-Darcy porous media. However, Kareem et al. [13] examined entropy production in a flow of couple stress liquid through permeable channel. The analysis was done by Adomian decomposition method. It was noticed from the investigation that magnetic field term reduces the entropy generation rate in the system. Despite many works done on couple stress fluid, to the best of the author's knowledge, no work has been done on the thermal runaway and entropy generation in an exothermic reactive couple stress fluid.

Studies associated to heat transfer and thermal runaway in a hydromagnetic exothermic reaction system is highly useful in enhancing operation and design of several technology devises[14, 15]. For example, the automobile's exhaust catalyst converter offers a stand for exothermic reaction in which hydrocarbons are totally burned. This supports the reduction of toxic emissions like carbon dioxide from engines that contaminant the environment [16, 17]. Nevertheless, to stabilize, ignite and work under steady state situations, the catalytic converter of a heat combustion criticality in a reactive couple stress needs to be obtained. Mathematically, heat transfer and thermal explosion of an exothermic chemical reaction institutes diffusion reactive problem and the longtime solutions performance in space will give a perception into the complex physical inherent process of thermal explosion system [18, 19].

The theory of diffusion reaction equations is relatively complex and their solution in spherical, rectangular and cylindrical coordinate remains highly essential and practically significance in technological sciences. This study examine the thermal explosion and entropy generation of reactive hydromagnetic couple stress fluid with dissipation and Navier slips under various kinetics using weighted residual method.

Consider an exothermic reacting fluid in a horizontal channel with unidirectional velocity distribution. The liquid is propelled by an external pressure gradient acting on the fully developed hydromagnetic fluid. The flow configuration contains a bounded infinite non-isothermal surfaces located atwith the-axis in the flow direction,is normal to the surfaces and the effects ofis negligible, see Fig. 1.

The mass conservation and a dynamically compatible flow motion equations for an incompressible, viscous couple stress liquid is written in the form Anwar et al. [20]

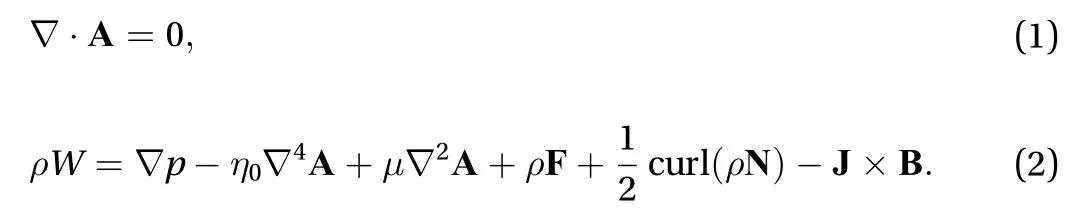
The parameter ratio to that of dynamic viscosity is squared units length which is the characteristic length of the material.The main idea of couple stress is the introduction of length dependent effect which can not be found in the dynamics of nonpolar classical fluid.

The moving conductor by Ohm's law in the present of Hall current can be written in the form

General equations of electromagnetic field by Maxwell's follows Stokes [21] is given as

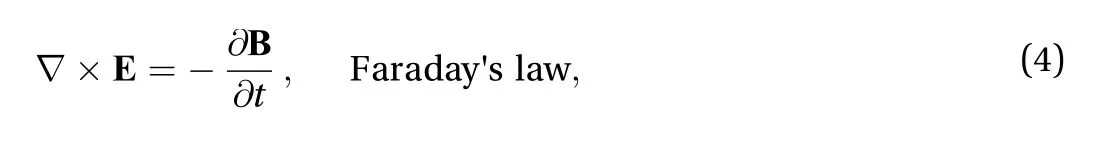
by Maxwell equation and

by Gauss's law.For

all over the liquid regime due to absent of external electrical field and negligible polarization effect. The energy balance equation for a couple stress exothermic chemical reaction is

where

represents internal energy,

is the heat flux by Fourier's law with thermal conductivity i.e.

. Follow from Okoya [22], temperature dependent reaction rate

is defined as

Applying the following non-dimensional quantities and variables on Eqs. (8)-(10) as

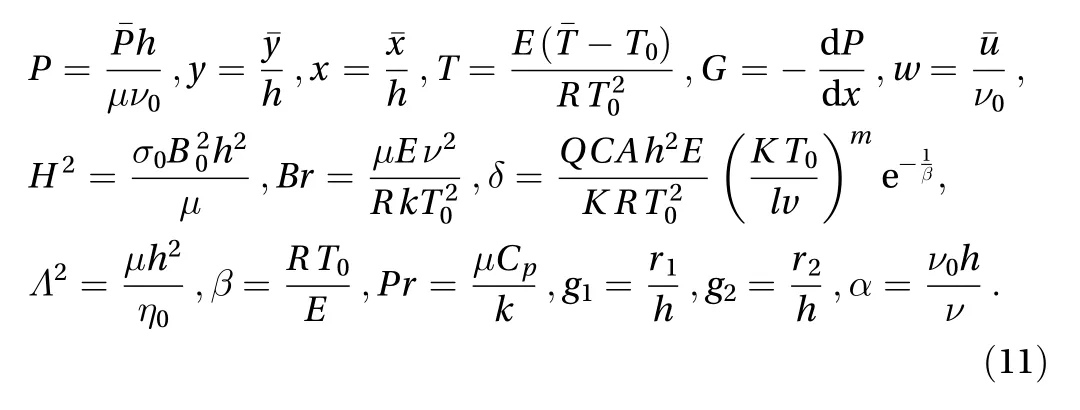
The following dimensionless equations are obtained

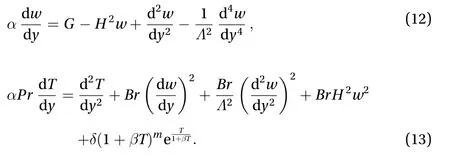
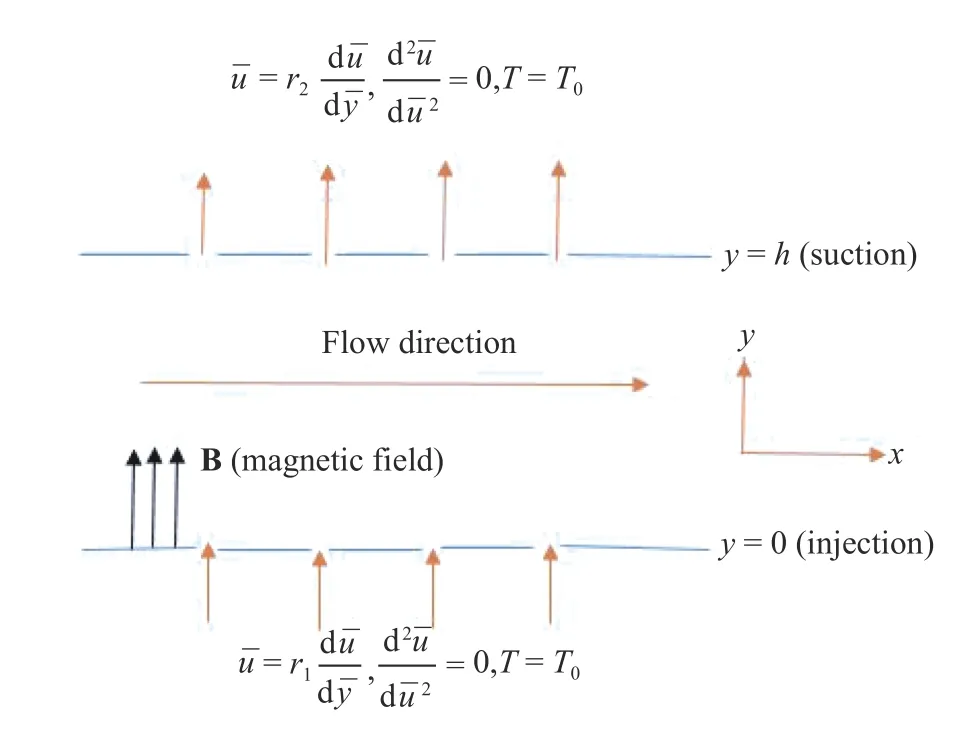
Fig. 1. Flow setup geometry

Along with the boundary conditions

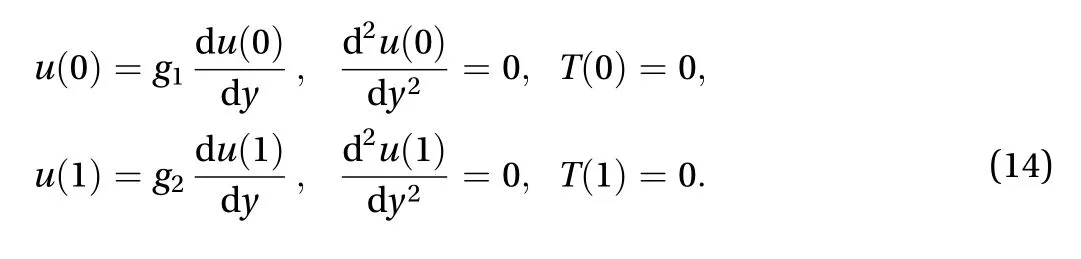
The wall shear stress friction and the wall temperature gradient for the purpose of engineering design are respectively defined as

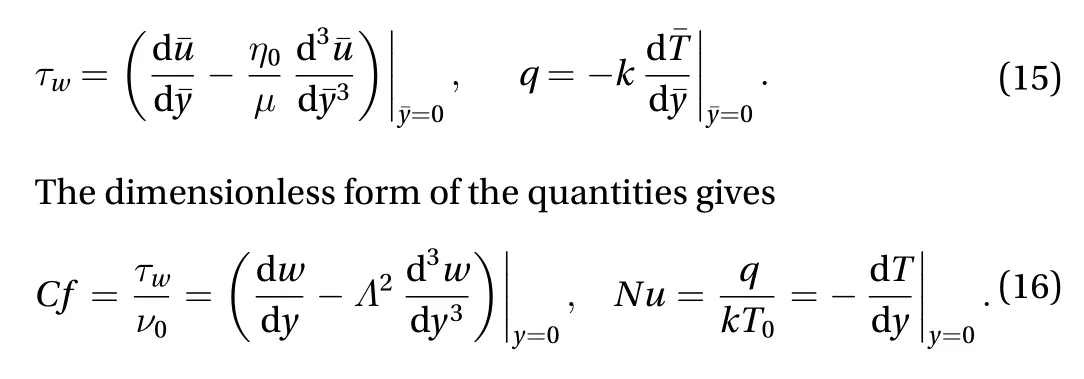
The inherently irreversible of the reactive hydromagnetic fluid flow creates consistence entropy generation. Thus, this is due to exchange of heat between the channel walls and the conducting couple stress fluid. The local entropy volumetric rate for the viscous fluid and magnetic fields is defined as [4, 23]

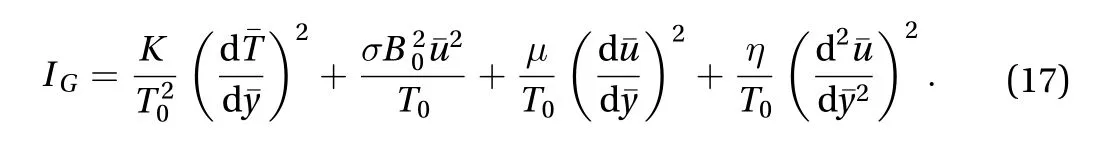
The first term of Eq. (17) defined the irreversibility of heat transfer while the irreversibility due to viscous joule heating, fluid friction and couple stress are respectively presented in the second to fourth terms of the equation. Using Eq. (11), the dimensionless rate of entropy generation in Eq. (17) takes the form

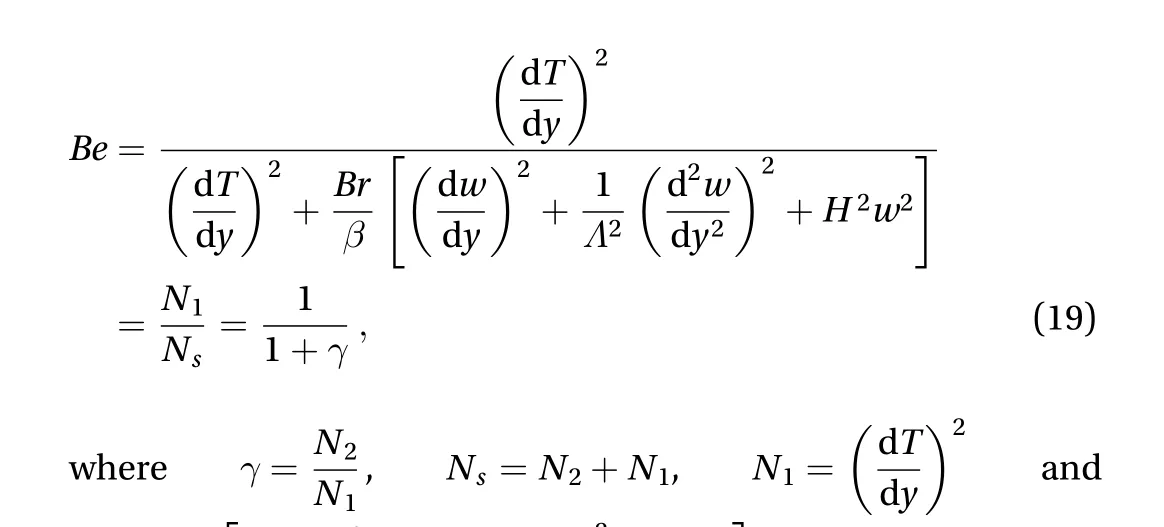
The weighted residual techniques [23, 24] is an idea that is based on getting an approximate solution to a differential equation in form of polynomial for an equation

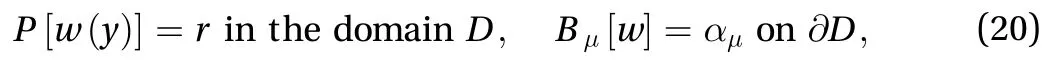
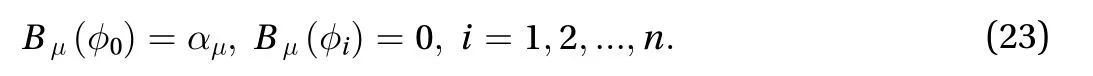
Therefore, the boundary condition of Eq. (20) is satisfied withfor arbitrary values of. Using Eq. (21) on Eq. (20), the residual equation is obtained as

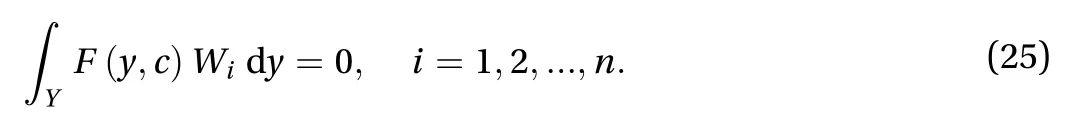
In the method, collocation techniques is adopted to provide solution to the weighted equations. The weight functions are taken to be Dirac delta function where. That is, the error is minimizedto zero at some assumed nodules.Integrationof Eq. (25) ofgives.

To solve Eqs. (12)-(14), a trial function is assumed as

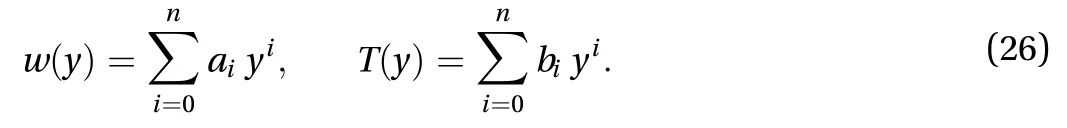
The trial function is imposed on the boundary conditions Eq. (14) as well on the Eqs. (12) and (13) to obtain the residual equations as follows

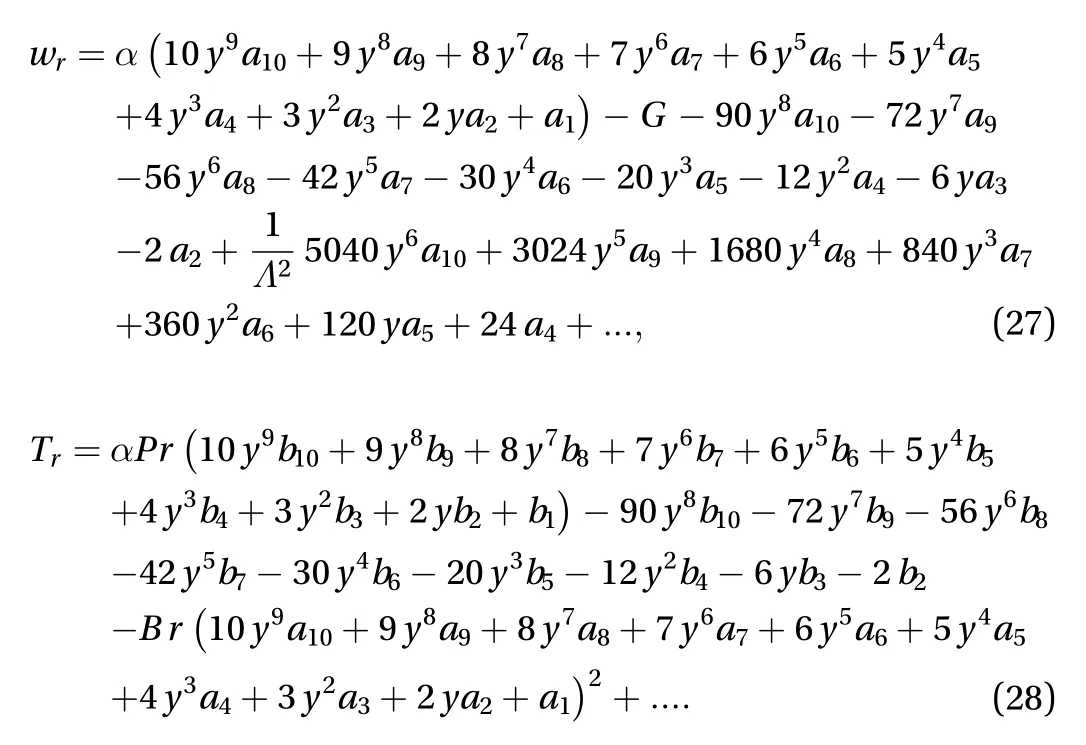
Within the domain, minimize the residual errors to zero at uniform interval of collocation points. That is,where, and,,. The residual equations along with the obtained boundary conditions are solved to get the unknown coefficients. The default parameters values are taken as,,,,,,,,,,. The process is repeated for variation in the parameters values. Maple software is used to solve for the unknown coefficients and for completely solving the problem.

In the study, semi-analytical method (collocation weighted residual method, CWRM) is used to obtain the solution to the problem under consideration. The influence of some thermophysical parameters on the reactive non-Newtonian fluid flow momentum, heat, entropy generation, Bejan number and thermal runaway are plotted and presented. It is illustrated in Table 1 that CWRM give a good result when compared with the exact results and Adominan decomposition method (ADM). The CWRM agree well with the other method of solutions with the order of absolute error. In Table 2, the numerical values for the wall shear stress friction and wall temperature gradient are reported. It is seen that some terms enhances or reduces the shear stress friction or heat gradient at the wall due to the influences of the momentum or temperature boundary layers.Figures 2 and 3 depict the reaction of the fluid momentum and temperature to variational increase in the inverse couple stress parameter. Physically, a rise in the inverse couple stress term leads to reduction in the fluid dynamic viscosity and amount of fluid additives. The decrease consequentially resulted into enhancement in the fluid velocity and energy transfer in the system. Meanwhile, an increase in the couple stress prompted production of velocity rotational field and non-Newtonian viscosity. Hence, a reduction in the momentum and heat distribution in an exothermic reaction is observed due to rise in the fluid friction. Figure 4 shows the effect of Hartmann number on the flow momentum field. Increasing the values of the termdiscourages the flow rate as the parameter enhances the reactive fluid drag force which resist the flow. The Lorentz force is boosted as the Hartmann number rises which in turn affected the fluid regime in the adjacent non-Newtonian liquid layer thereby diminishes the profile. The impact of Brinkman number on the energy distribution is displayed in Fig. 5. It is seen from the plot that a rise in the termstimulated the viscous heating source term in the heat equation that causes more heat to be generated in the reactive exothermic system. An increase in theheat generation reduces the intermolecular cohesion, this then resulted in free and high collision of the fluid particles and thereby rises the heat field in the channel.

Table 1 Results comparison with the existing results and analytical for velocity profile when,,,

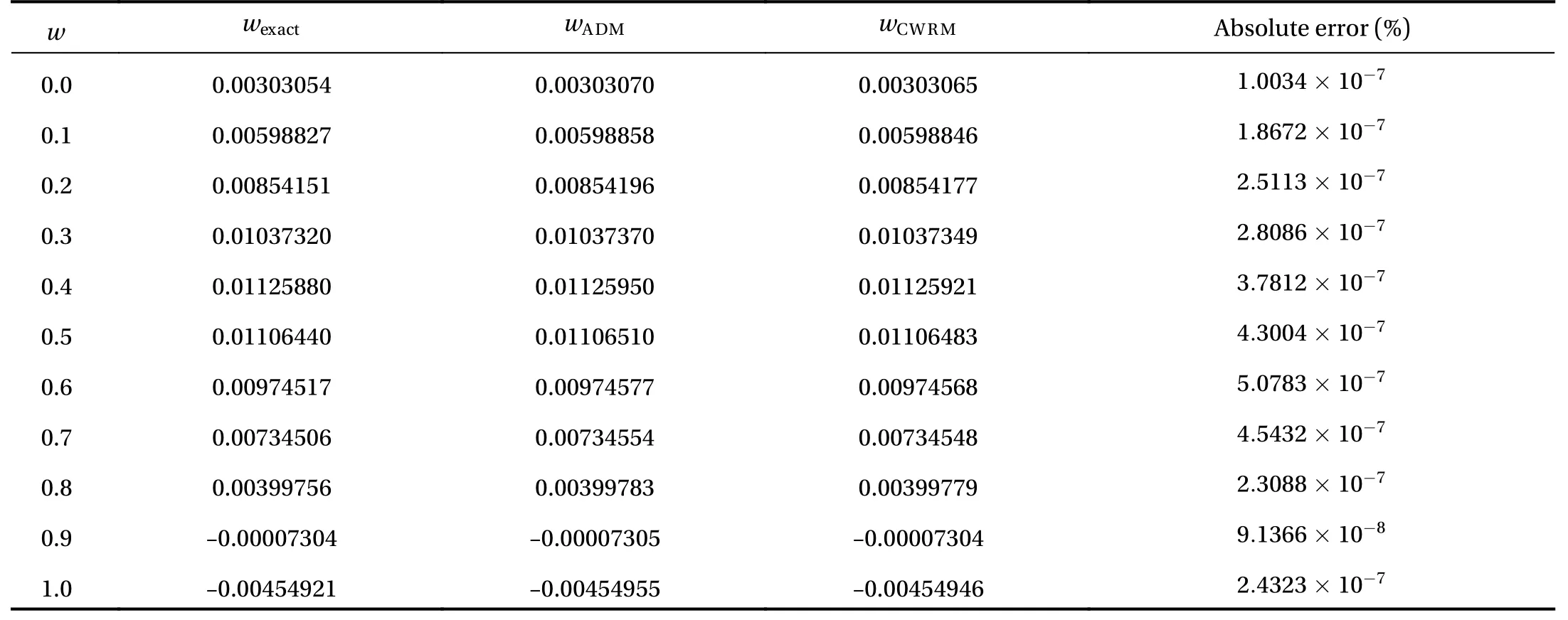
Table 1 Results comparison with the existing results and analytical for velocity profile when,,,

images/BZ_43_225_2323_254_2344.png images/BZ_43_500_2310_584_2339.png images/BZ_43_953_2310_1040_2339.png images/BZ_43_1395_2310_1507_2339.png Absolute error (%)0.0 0.00303054 0.00303070 0.00303065images/BZ_43_1899_2378_2111_2415.png0.1 0.00598827 0.00598858 0.00598846images/BZ_43_1899_2449_2111_2486.png0.2 0.00854151 0.00854196 0.00854177images/BZ_43_1899_2520_2111_2557.png0.3 0.01037320 0.01037370 0.01037349images/BZ_43_1899_2590_2111_2628.png0.4 0.01125880 0.01125950 0.01125921images/BZ_43_1899_2661_2111_2699.png0.5 0.01106440 0.01106510 0.01106483images/BZ_43_1899_2732_2111_2770.png0.6 0.00974517 0.00974577 0.00974568images/BZ_43_1899_2803_2111_2840.png0.7 0.00734506 0.00734554 0.00734548images/BZ_43_1899_2874_2111_2911.png0.8 0.00399756 0.00399783 0.00399779images/BZ_43_1899_2945_2111_2982.png0.9 -0.00007304 -0.00007305 -0.00007304images/BZ_43_1899_3015_2111_3053.png1.0 -0.00454921 -0.00454955 -0.00454946images/BZ_43_1899_3086_2111_3124.png

The effect of selected terms on the entropy production rate and irreversibility ratio are respectively presented in Figs. 6-9.The response of entropy generation rate and Bejan number on an increase in the Frank-Kamenetskiiand pressure gradientterms are illustrated. It is seen from the diagram that risingin the Frank-Kamenetskii values increases steadily the rate of entropy generation and Bejan number at the upper surface of the wall towards the center of the channel where an insignificant effect is noticed. At the center of the channel irreversibility process is at it peak and Bejan number is at it lowest. Hence,gradual rise toward the free stream is observed as the heat transport irreversibility control the non-Newtonian exothermic reaction. An enhancement in the flow pressure gradient term is seen to have simulated heat source term and discourages the fluid bonding forces, this turn to increase the thermodynamic process within the system and thereby rises the irreversibility process due heat transfer, joule heating and couple stress. Therefore, the Bejan number and entropy generation distribution is increased.

Table 2 Numerical values for the shear stress friction and temperature gradient.

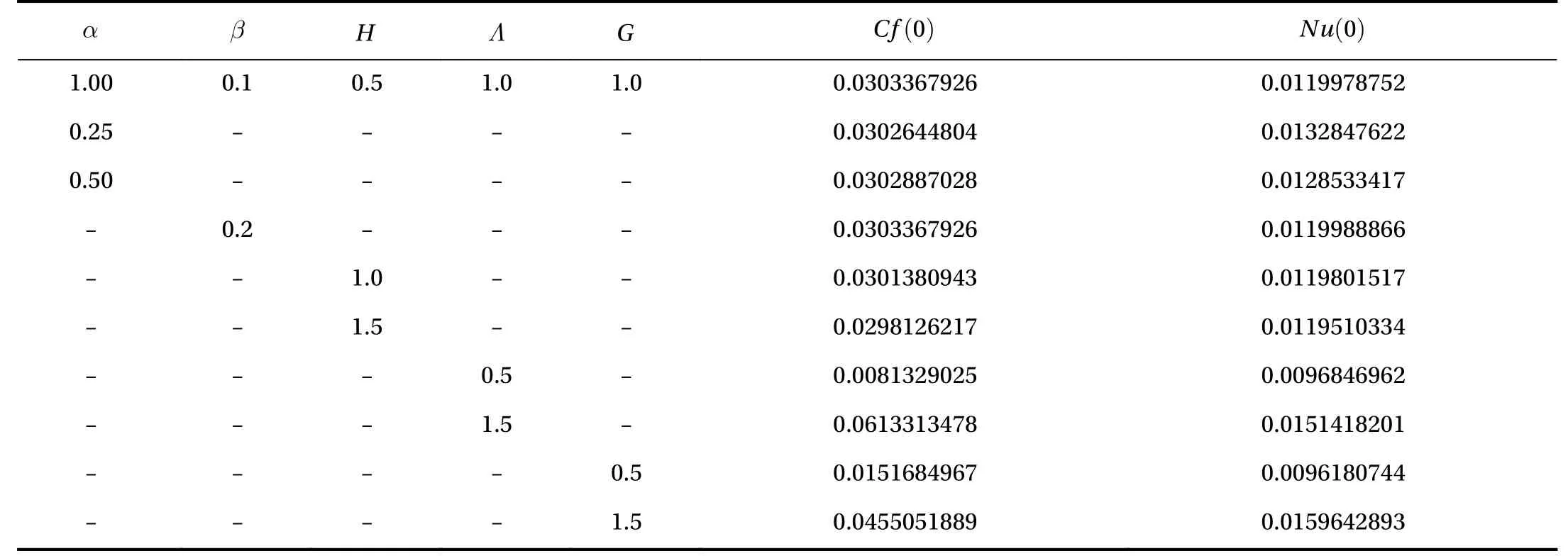
Table 2 Numerical values for the shear stress friction and temperature gradient.

images/BZ_44_226_723_251_744.pngimages/BZ_44_434_715_455_752.pngimages/BZ_44_611_719_644_748.png images/BZ_44_798_719_823_748.pngimages/BZ_44_978_719_1008_748.png images/BZ_44_1340_711_1432_757.pngimages/BZ_44_1941_711_2037_757.png1.00 0.1 0.5 1.0 1.0 0.0303367926 0.0119978752 0.25 - - - - 0.0302644804 0.0132847622 0.50 - - - - 0.0302887028 0.0128533417- 0.2 - - - 0.0303367926 0.0119988866- - 1.0 - - 0.0301380943 0.0119801517- - 1.5 - - 0.0298126217 0.0119510334- - - 0.5 - 0.0081329025 0.0096846962- - - 1.5 - 0.0613313478 0.0151418201- - - - 0.5 0.0151684967 0.0096180744- - - - 1.5 0.0455051889 0.0159642893

Fig. 2. Velocity profile with rising

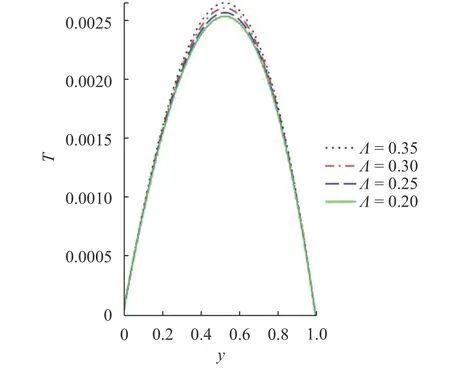
Fig. 3. Heat profile with rising

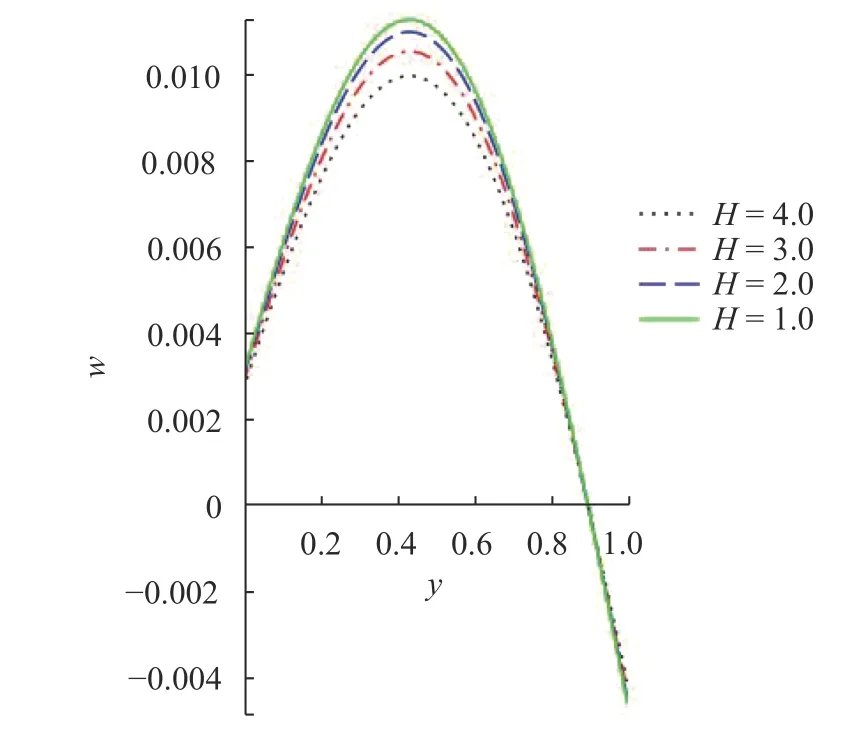
Fig. 4. Velocity profile with rising

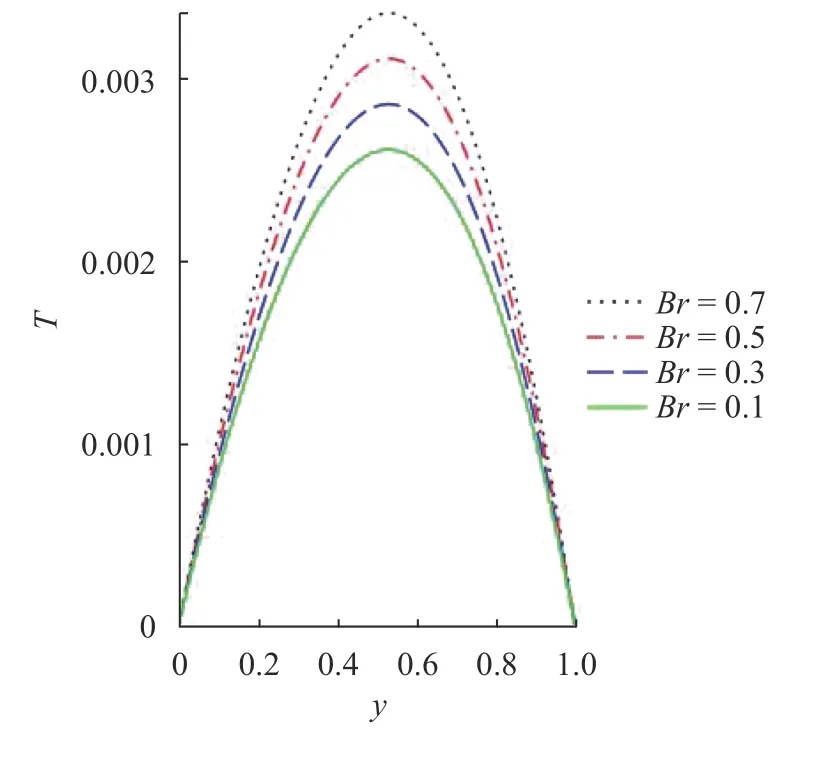
Fig. 5. Heat profile with rising

Figures 10-12 represent the bifurcation diagram for the branched-chain thermal criticality with various chemical kinetics. Thermal criticality is a state where a rise in heat changes the system conditions such that it leads to more rise in heat, this leads to solution blowup result. The plots ofagainstfor hydromagnetic couple stress chemical reactive with Navier slips is reported. The results are obtained when, no real results takes place but a classical one depicting the thermal explosion is seen. The couple stress viscosity reduces as the internal heat increases. Flow rates gradient rises with temperature and causes solution flow back in the heat equation, leading to thermal runaway. The results show that when the chemical kinetic is,, at,while for,. From the results, a decrease in the criticality is noticed as the chemical kinetics increases.

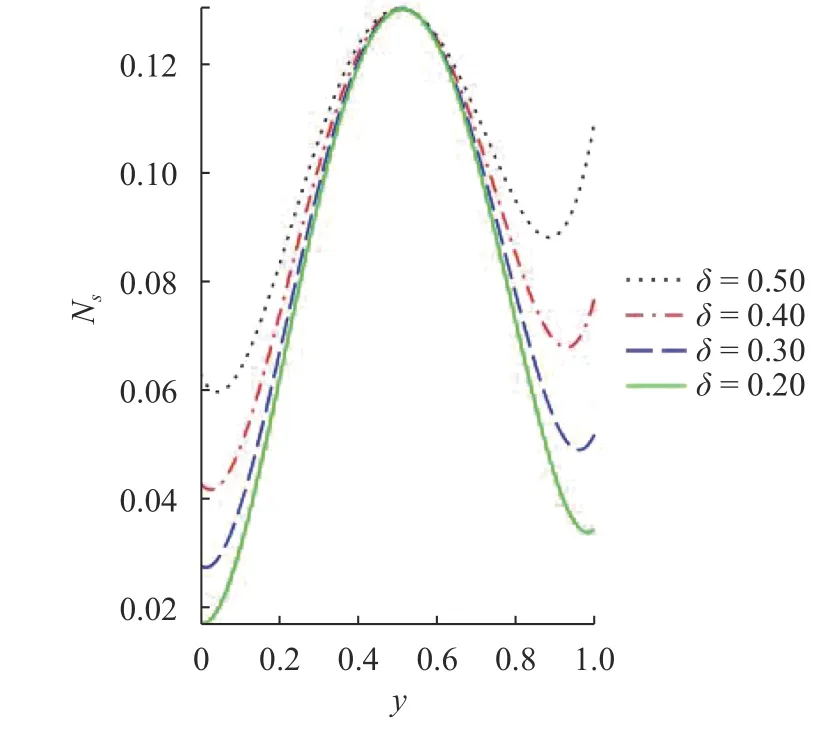
Fig. 6. Entropy generation with rising

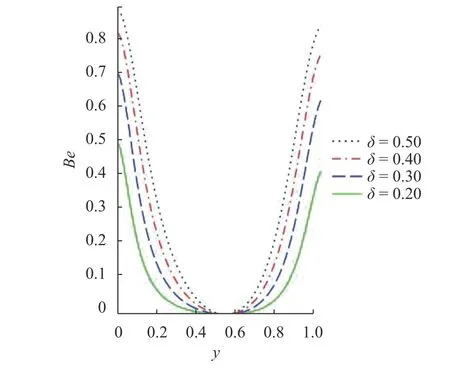
Fig. 7. Bejan number with rising

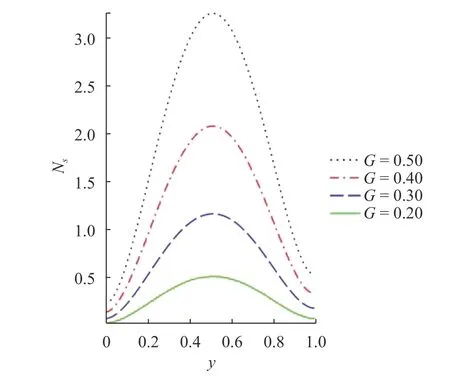
Fig. 8. Entropy generation with rising

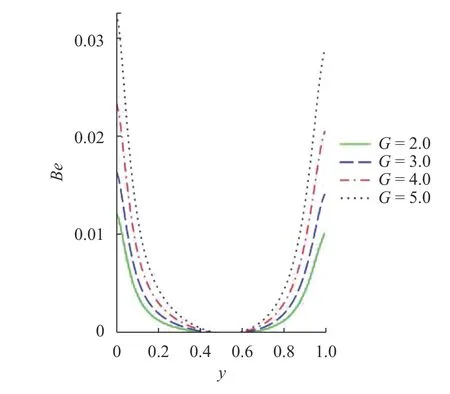
Fig. 9. Bejan number with rising

Fig. 10. Explosion bifurcation with

Fig. 11. Explosion bifurcation with

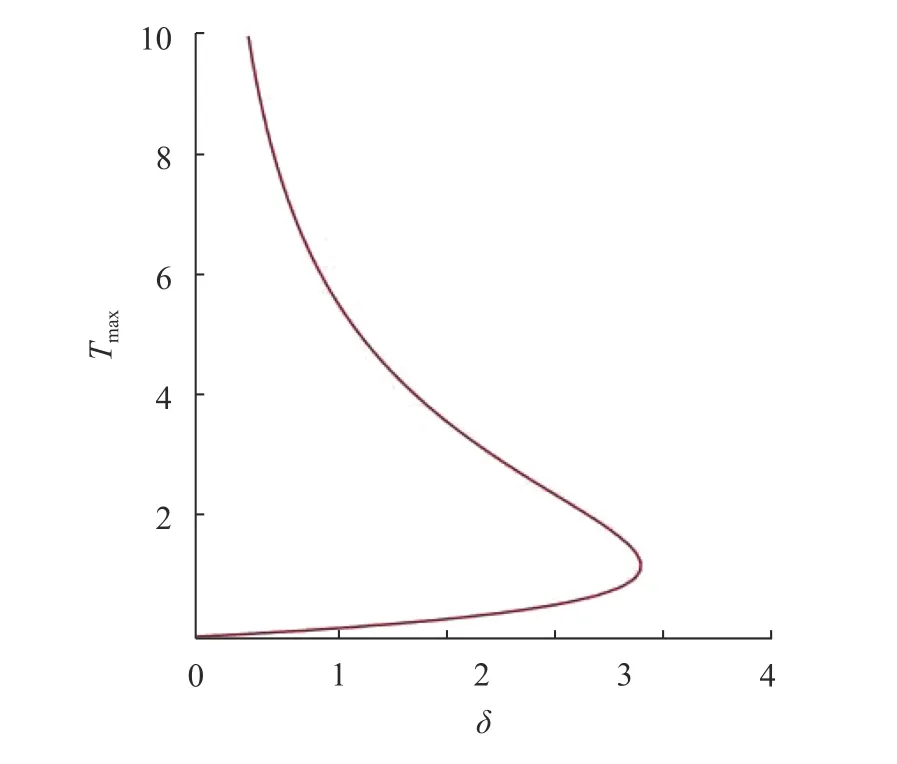
Fig. 12. Explosion bifurcation with

In the work, an equation for an inhomogeneous spatially system for couple stress thermal reaction with Navier slips was developed and analytically solved using collocation weighted residual method. From the study, thermal explosion branchedchain structure was established as compared to the traditional theory of thermal explosion. It is seen from the work that the momentum and heat fields is diminished or enhanced, due to the impact of inhomogeneity or homogeneity parameters in a reactive couple stress fluid. The heat transfer irreversibility and irreversibility due to viscous Joule heating and couple stress, is observed increasing as the Frank-Kamenetskii and pressure gradient terms rises. The increment is due to an increase in the internal heat generation. Hence, to reduce irreversibility process in a system, the dissipation rate, viscosity and hysteresis magnetic influences should be reduced. When the unsteady solution forat some points in the main equation is infinite say in a finite time such is characterized as thermal explosion. Therefore, there is need to examine and guard the choice of values forthat resulted in solution blowup. The present results, in chemistry with suitable and detailed approximations can be useful in oxygen or air mixtures, hydrocarbons, fuels and many others.

Nomenclature

?:Reactantspecies

Greek symbols