Numerical analysis of a simplest fractional-order hyperchaotic system

Dong Peng, Kehui Sun, Shaobo He, Limin Zhang, Abdulaziz O. A. Alamodi

School of Physics and Electronics, Central South University, Changsha, Hunan 410083, China

Keywords:Chaos Fractional calculus Simplest fractional-order hyperchaotic system Adomian decomposition method DSP implementation

A B S T R A C T In this paper, a simplest fractional-order hyperchaotic (SFOH) system is obtained when the fractional calculus is applied to the piecewise-linear hyperchaotic system, which possesses seven terms without any quadratic or higher-order polynomials. The numerical solution of the SFOH system is investigated based on the Adomian decomposition method (ADM). The methods of segmentation and replacement function are proposed to solve this system and analyze the dynamics. Dynamics of this system are demonstrated by means of phase portraits, bifurcation diagrams, Lyapunov exponent spectrum (LEs) and Poincaré section. The results show that the system has a wide chaotic range with order change, and large Lyapunov exponent when the order is very small, which indicates that the system has a good application prospect. Besides, the parameter a is a partial amplitude controller for the SFOH system. Finally, the system is successfully implemented by digital signal processor (DSP). It lays a foundation for the application of the SFOH system.

With the rapid development of the computer science and engineering technology, the research of fractional-order calculus has become one of hot topics in the field of nonlinear science[1-3]. Compared with integer-order chaotic systems, their fractional-order counterparts usually exhibit more complex behaviors [4-6]. In the meantime, the problem of solving fractional-order differential equations have also attracted the interest of many scholars. So far, three approaches are mainly derived to solve fractional-order differential equations: frequency-domain method (FDM) [7], Adams-Bashforth-Moulton (ABM) algorithm[8], and Adomian decomposition method (ADM) [9]. Recently,ADM is widely used because of its high accuracy and fast convergence in dealing with nonlinear equations. Some scholars have studied some typical chaotic systems with fractional-order version based on this method. For example, Capfagna et al. [10, 11]investigated the bifurcation and chaos in the fractional-order Chen system and hyperchaos in the fractional-order Rössler system. Xu et al. studied the dynamics of fractional-order simplified unified system [12]. Zhang et al. [13] analyzed the solution and dynamics of a fractional-order five-dimensional (5D) hyperchaotic system with four wings. However, these researchers only involve the nonlinear terms about the product of two state variables. And up to now, no one has studied the fractional-order chaotic systems that contain especial nonlinear items like an absolute value function or a sign function. So the treatment of the type of fractional-order nonlinear equation base on the ADM algorithm will be an interesting work.

Dynamical behaviors of hyperchaotic systems are more difficult to be predicted, so it owns higher security compared with chaotic system in secure communication applications [14-16].Hyperchaotic systems are usually derived from the expansion of three-dimensional chaotic systems [17, 18]. Therefore, their systems model are often more complex than corresponding original model. Recently, Li et al. [19] proposed a new piecewise-linear (PWL) hyperchaotic system, which only possesses seven terms without any quadratic or higher-order polynomials, and the nonlinear terms are an absolute value function and a sign function. To our knowledge, it is the simplest hyperchaotic system. Moreover, the PWL hyperchaotic system was implemented by analogy circuit. The piecewise continuous functions in fractional-order system is studied in Ref. [20] and the rigorous mathematical justification is given. However, there are no works to solve these functions in fractional-order version by using ADM.So, we will solve the simplest fractional-order hyperchaotic(SFOH) system by applying ADM algorithm.

The circuit realizations of chaotic systems are conducive to its practical application [21]. In recent years, some peoples devoted to the circuit implementation of a fractional-order chaotic systems. Han et al. [22] studied the fractional-order hyperchaotic Liu system and its circuit realization. El-Sayed et al. [23] implemented the circuit of a new fractional-order hyperchaotic system. In recent years, digital signal processor (DSP) is more popular than analog circuit implementation in engineering because of its performance and simplicity in signal processing[24, 25]. It has excellent reliability and accuracy for the application of fractional-order hyperchaotic systems. Therefore, it is worthy to apply the digital signal processor to the SFOH system.

Several definitions exist regarding the fractional calculus,and Caputo derivation and Riemann-Liouville (R-L) integration are two most commonly used calculus definitions.

Definition 1[26] The Caputo fractional-order derivation of a functionis defined as

Definition 2[26] The Riemann-Liouville (R-L) fractional integration of a functionis given by

Consider a nonlinear fractional differential equationwhereare state variables, andis the constant for the autonomous system. The functioncan be separated into two terms[27-29], then the differential equation becomes to

Based on the ADM algorithm, the numerical solution of the Eq. (6) is expressed as

The equation of the integer-order PWL hyperchaotic system is proposed [19]

Here, the nonlinear terms include the absolute value function and the signum function. To obtain the numerical solution,we adopt the segmentation method to deal with the nonlinear parts. So, the Eq. (12) are expressed as

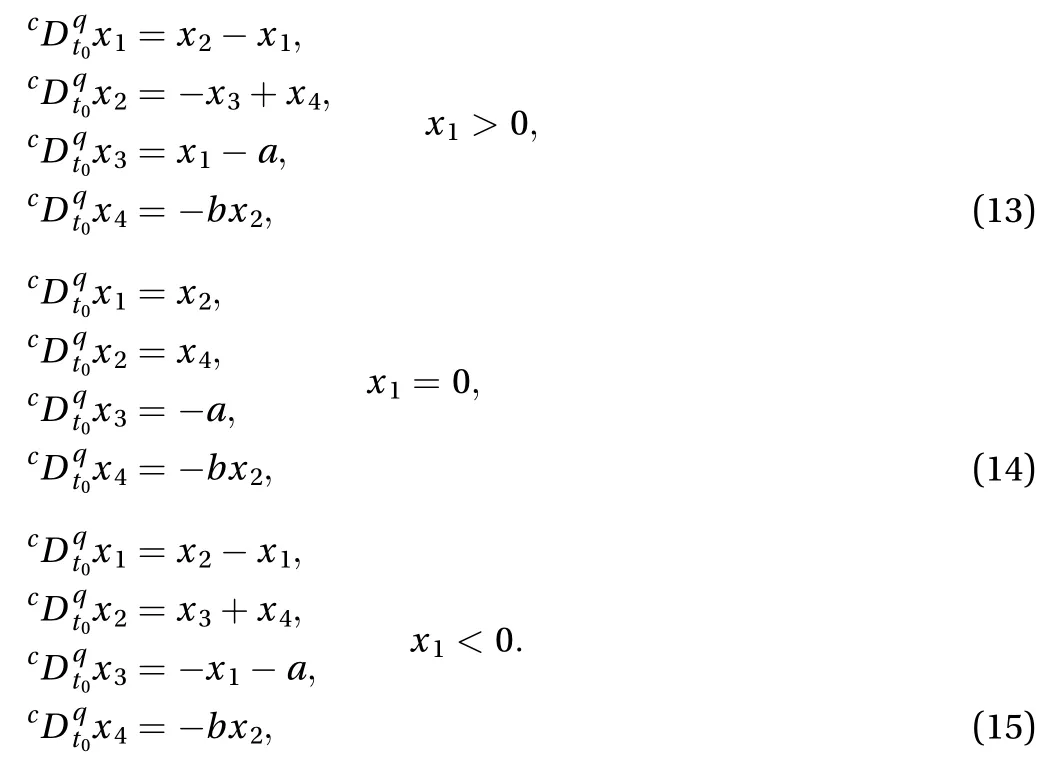
It is interesting that no one of these three equations contain nonlinear terms. We set the initial conditions:andSince the nonlinear terms are not included in Eqs. (13)-(15), there is no decomposition part inthe solution.So,the solution ofthe system (12) becomes simpler. The-term approximate vector solutionis defined as:

The exact solution can be obtained whentends to infinity,but considering the practical situation,is sufficient for precision. According to the Eq. (10) and the properties Eqs. (3)and (4). When, the first few terms of the decomposition series are given by

Thus, the analytic solution with the time ofis obtained. In order to get the solution at the time ofthe calculation of solution inevitably involves time discretization. The intervalis divided into several subintervalsMaking the solution at the timeequal to initial value, based on the iterative sequence of Eq. (26), then we obtain the value in timeAccording to the rule, a series of data is obtained, and the simulation results of attractor phase diagrams of SFOH system are shown in Fig. 1. The calculation step size is 0.01, and the initial values are, and the system parameters are

In this paper, we use bifurcation diagrams and Lyapunov exponent spectrum (LEs) to analyze the dynamic characteristics of the SFOH system. Through these two analysis methods, we can clearly see the evolution process of the system as the parameters change. As we all know, several calculation methods exist to calculate the Lyapunov exponent (LE) [30]. Compared with other methods, the QR decomposition method [31] has the advantage of fast convergence. So it is chosen to draw the LEs of the SFOH system. However, for this nonsmooth systems, because of the discontinuous absolute and signum functions, it does not work satisfactorily to calculate the LEs [32]. To calculate LEs correctly,the absolute and signum function is replaced by continuous equivalents. The graph ofis shown in Fig.2(a), and it is clearly that, as the increase ofthe curve ofis close to the curve of. So, theis replaced byand theis replaced byThis replacement function is extremely approximate whenThe new system equation is shown as follows.

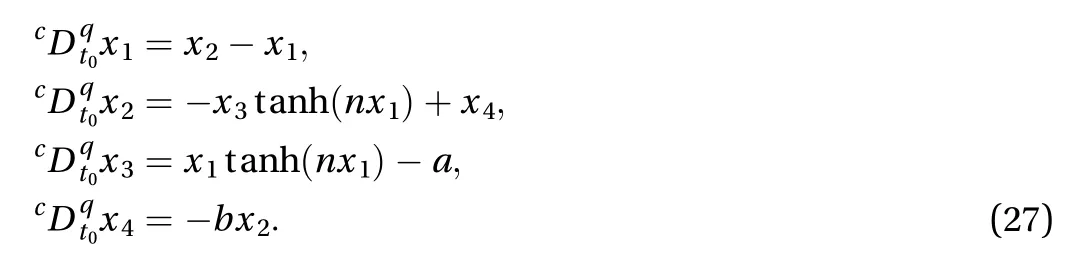
Based on the above steps, the first four Adomian polynomials for the nonlinear termare

Fig. 2. Graph of and. a Curves of with different curve of

Fig. 3. Bifurcation diagram and Lyapunov exponent spectrum of the system (12) with change when Bifurcation diagram, Lyapunov exponent spectrum

Fig. 4. 0-1 test with different = 0.178

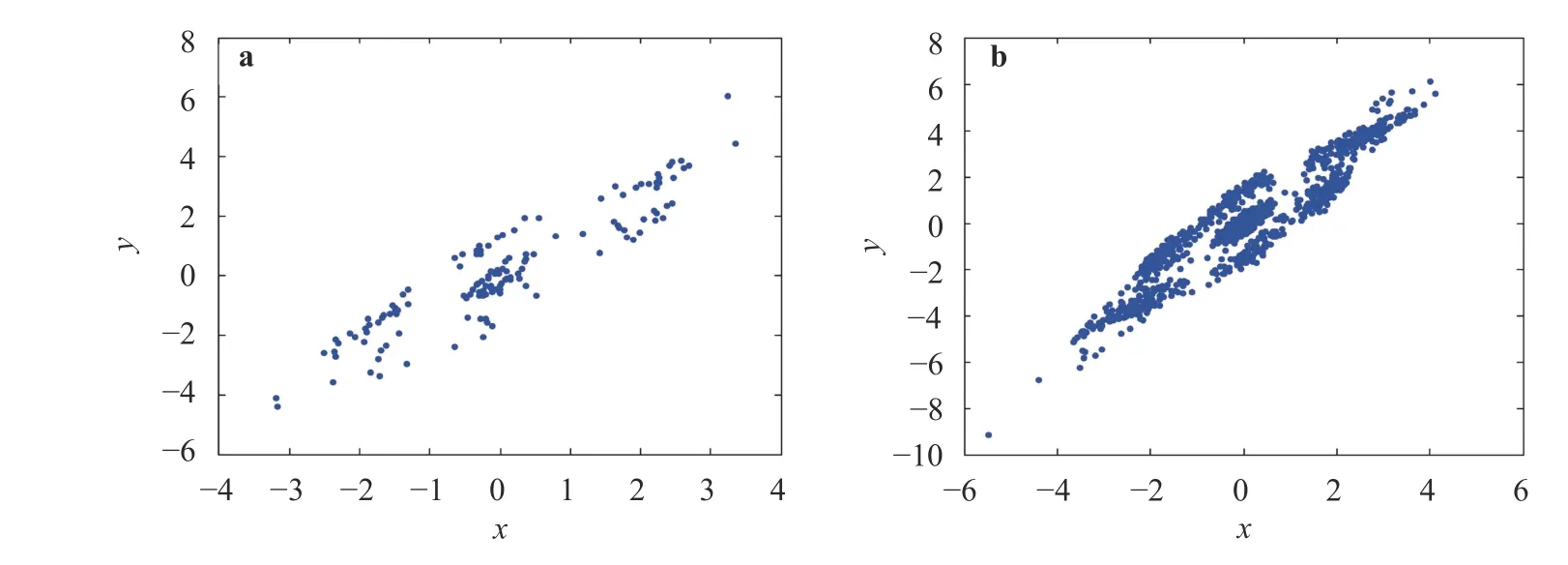
Fig. 5. Poincaré sections of system (12) for different(hyperchaotic)

Fig. 6. Bifurcation diagram and Lyapunov exponent spectrum of the system (12) with change when Bifurcation diagram, b Lyapunov exponent spectrum

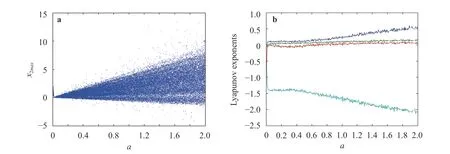
Fig. 7. Bifurcation diagram and Lyapunov exponent spectrum of the system (12) withchange when Bifurcation diagram, b Lyapunov exponent spectrum

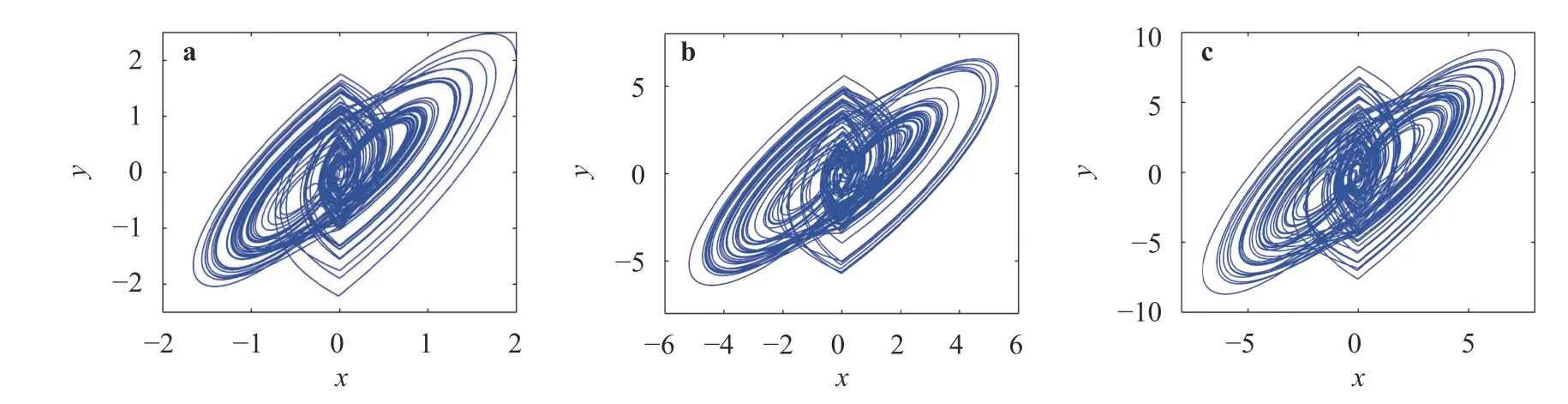
Fig. 8. Chaotic attractors with different value of

(4) Chaos diagram is a comprehensive way to reflect dynamics of a chaotic system in the double parameters space. In this paper, we plot the chaos diagram based on complexity algorithm. Currently, some complexity measure methods are proposed to evaluate the chaotic system such as Kolmogorov-Sinai Entropy [39], Spectral Entropy (SE) [40], and Fuzzy Entropy [41].For fractional-order chaotic systems, Spectral Entropy has the properties of simplicity, robustness and extremely fast calculation. So it is a appropriate choice to analyze the complexity of the SFOH system. Chaos diagram based on SE complexity in the

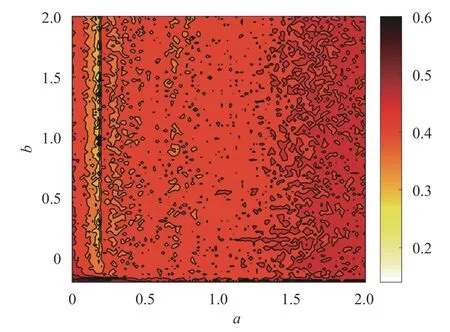
Fig. 9. Chaos diagram based on SE complexity in the plane with

For the practical application of the SFOH system, we design and implement the SFOH system by a the DSP digital circuit.The hardware experimental equipments are shown in Fig. 10. It contains the DSP development board (TMS320F28335), the digital to analog conversion module (DAC8552) and the oscilloscope. The DSP development board can make a great match with the 16 bit channel DAC8552, it controls the DAC8552 through a serial peripheral interface (SPI). Finally, based on the great powerful computing ability of DSP, the attractors of the chaotic system clearly and real - time are displayed to the oscilloscope.

Fig. 10. The device of DSP to implement a fractional-order chaotic system

Fig. 11. Attractors of system (12) implemented on DSP with and initial conditions (0, 1, 1, 1). plane, bplane, plane, plane

In this paper, we investigated the solution of SFOH system based on the ADM algorithm. The dynamics of the fractional-order system are analyzed by bifurcation diagrams, Lyapunov exponent spectrum and Poincaré section. Finally, the SFOH system is implemented on DSP. The conclusions are drawn as follows: (i) To solve and analyze the SFOH system, we applied the methods of segmentation and replacement function. The results show that the proposed methods are effective to deal with the SFOH system; (ii) The lowest order is 0.534 under the condition of parameters0.25, and the maximum Lyapunov exponent is large with small order, which represent that the system has better application prospect than its corresponding integerorder chaotic system. Moreover, the system parametercan be taken as a amplitude control in the SFOH system; (iii) The SFOH system is implemented by DSP digital circuit, and it plays a hardware foundation for its applications in secure communication.Next work, we will focus on the synchronization of SFOH system based on ADM algorithm.

Acknowledgement

This work is supported by the National Natural Science Foundation of China (61161006 and 61573383). This work is supported by the Research and Innovation Project of Graduate Students of Central South University (2018ZZTS348).