On the Weissenberg effect of turbulence

Yu-Ning Huang*, Wei-Dong Su, Cun-Biao Lee

State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, China Dedicated in memory of Clifford Truesdell on the occasion of his 100th Anniversary

Keywords:Normal stress difference Natural time of turbulence Weissenberg number of turbulence Elastic effect Non-Newtonian fluid

A B S T R A C T Within the framework of the Navier-Stokes equations, the Weissenberg effect of turbulence is investigated. We begin with our investigation on the elastic effect of homogeneous turbulent shear flow. First, in the sense of Truesdell (Physics of Fluids, 1964) on the natural time of materials, we derive the natural time of turbulence, and use it together with the natural viscosity of turbulence derived in the article of Huang et al. (Journal of Turbulence, 2003) to define the natural Weissenberg number of turbulence as a measure of the elastic effect of homogeneous turbulence.Second, we define a primary Weissenberg number of turbulence, which in laminar flow reduces to the Weissenberg number widely applied in rheology to characterize the elasticity of visco-elastic fluids. Our analysis based on the experimental results of Tavoularis and Karnik (Journal of Fluid Mechanics, 1989) indicates that the larger is the Weissenberg number of turbulence, the more elastic becomes the turbulent flow concerned. Furthermore, we put forth a general Weissenberg number of turbulence, which includes the primary Weissenberg number of turbulence as a special case, to measure the overall elastic effects of turbulence. Besides, it is shown that the general Weissenberg number can also be used to characterize the elastic effects of non-Newtonian fluids in laminar flow.

1 Introduction

It is well known that one of the most famous actions of normal stress differences is the appearance of the Weissenberg effect in a visco-elastic fluid. In his celebrated article entitled “A continuum theory of rheological phenomena”, Weissenberg [1]reported the so-called rod-climbing phenomenon in laminar flow of a visco-elastic fluid, a popular phenomenon that can be observed in daily life when one stirs a bowl of cake batter or a can of paint—though, interestingly, this phenomenon can never be seen in laminar flow of a Newtonian fluid, such as drinking water. In fact, it is the inequality of the normal stresses, a.k.a. the normal stress effect or the Weissenberg effect, that plays a vital role in this rod-climbing phenomenon of a fluid. The normal stress effect of a visco-elastic fluid generated in a viscometric flow, i.e., the Weissenberg effect, is the equivalent of the Poynting effect [2] in a nonlinear elastic material—that is, to produce a state of simple shear in a nonlinear elastic material, normal stresses as well as a shear stress are needed, and the normal stresses are unequal. It was Truesdell [3] who first proposed in 1952 to call this phenomenon the Poynting effect. Interestingly,both well-known effects are a direct consequence of non-zero normal stress differences of the materials under shear or shearing.

In this work, we shall investigate the elastic effects of the turbulence of an incompressible Newtonian fluid. An incompressible Newtonian fluid is purely viscous, exhibiting no elastic effect, as can be read off from its constitutive equation

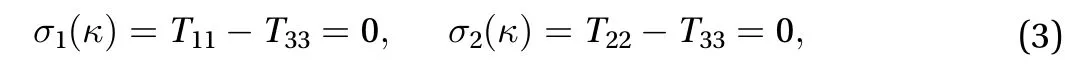
By contrast, the turbulent Newtonian fluid generally behaves like a non-Newtonian fluid that exhibits nonlinear visco-elastic and memory effects. For instance, Rivlin [4] noted that some analogy may exist between the turbulent Newtonian fluid and the laminar flow of a non-Newtonian fluid and suggested that there may occur the normal stress effect in a turbulent Newtonian fluid. Also, Liepmann [5] suggested that a non-Newtonian fluid constitutive equation for turbulence may be able to account for the large-eddy structures and self-excited oscillations of turbulent boundary layers. Townsend [6] studied the phenomenon of entrainment in free turbulent flows and concluded that the initial response of turbulence to distortion is elastic in character.Crow [7] investigated the relaxation effects in turbulent flow of an incompressible Newtonian fluid and pointed out that the turbulence responds initially to an arbitrary deformation like an elastic medium. By employing the methods and reasoning of rational mechanics, Lumley [8] showed that in homogeneous turbulent shear flow the turbulence of a Newtonian fluid has the same behavior as that of a nonlinear visco-elastic fluid, a simple fluid in the sense of Noll [9]. Speziale [10] and Huang and Rajagopal [11] investigated respectively, among others, the origin of the turbulent secondary flow of a Newtonian fluid in a straight tube of non-circular cross-section, which actually is a normal stress effect. She et al. [12] performed numerical simulations to study the visco-elastic behavior of a turbulent Newtonian fluid.Huang et al. [13] proved the existence of the natural viscosity of turbulence of a Newtonian fluid based on the Reynolds stress transport equation, which is comparable to the existence of the natural viscosities, in the sense of Truesdell [14, 15], of a large number of non-Newtonian fluids which are special cases of the simple fluid of Noll [9].

Here, we consider an incompressible Newtonian fluid with constant mass densityand viscosityThe linear momentum equations, i.e., the Navier-Stokes equations, and the continuity equation read

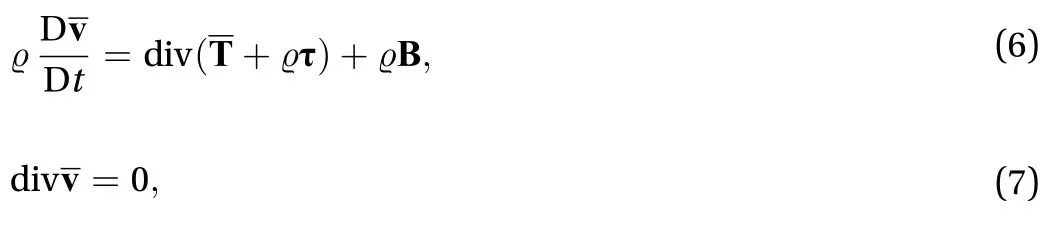
Taking the ensemble average on the above equations gives in which an overline represents the ensemble average,denotes the material time derivativeassociated with the mean

Subtracting Eq. (6) from Eq. (4) results in the evolution equation for the fluctuating velocity

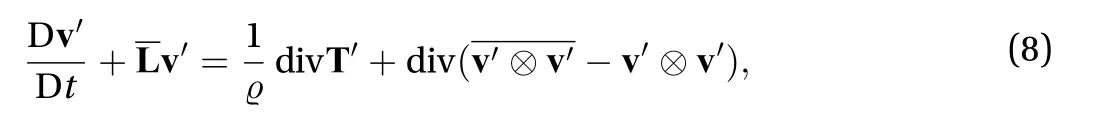
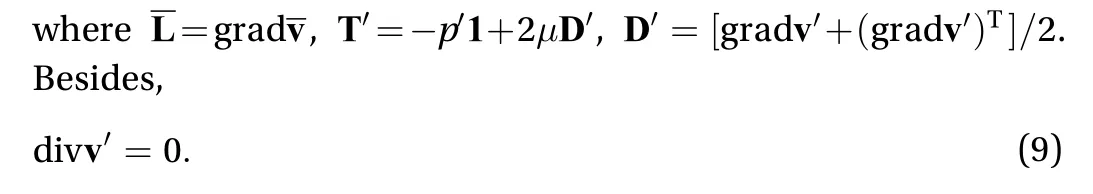
The Reynolds stress transport equation derived from the evolution equation for the fluctuating velocitytakes the form

Here, in retrospect, it is worth noting that the two seminal papers of Chou [16, 17] published in 1940 and in 1945, respectively, made remarkable contributions to the foundation of turbulence modelling based on the Reynolds-averaged Navier-Stokes equations, namely the so-called RANS approach in modern times that has a far-reaching influence, see also Chou and Chou [18], Lumley and Yaglom [19] for details. Indeed, the socalled second-order closure of turbulence is about closing the Reynolds stress transport equation by modelling the unknown terms that appear in it, which had its beginning with the aforementioned Chou's work in the 1940s, as shown in the work of Rotta [20], Launder et al. [21], Fu et al. [22]; see also the articles of Launder [23], and Girimaji [24].

Before proceeding to investigate the elastic effects of turbulence, let us have a brief look at some previous researches on the normal stress differences, the cause of the elastic effects, of non-Newtonian fluids. Truesdell [25] showed that in simple shearing flow, the normalstress differencecanbe used to determinethe response timeof a fluid of the second grade,which may be regarded as a fluid with convected elasticity, a special case of the simple fluid of Noll [9]. In discussing drag reduction phenomenon, i.e., the so-called Toms effect, Lumley [26]in 1969 pointed out that in a viscometric flow of a non-Newtonian fluid, elasticity plays a vital role in drag reduction in the flows and, in particular, the normal stress differenceis a direct measure for the visco-elastic effects, and concluded that elasticity is essential for the drag reduction phenomenon. Boger[27] mentioned that it has become customary to characterize the elasticity of visco-elastic fluids on the basis of observed steady shear flow properties in a viscometric flow. He further pointed out that a characteristic timeis generally used to describe the elasticity of fluid, showing that thecharacteristic timefora Maxwell fluid iswhereis the shear rate andis the viscosity.

2 The natural time of turbulence

2.1 The concept of the natural time of a simple fluid

In the late 1940s and early 1950s, Truesdell remarked that every visco-elastic substance has a natural time and indicated how to define such a time and measure it (see Refs. [3, 14] by Truesdell). In this important article with great insight, as was also made clear in his 1964 article [14], Truesdell [3] pointed out that all calculations of normal stress effects presume the existence of a natural time. In other words, the natural time of a visco-elastic fluid is intrinsically related to the normal stress differences of the fluid in question. Indeed, in 1964 Truesdell [14]introduced the notion of the natural time for a simple fluid in the sense of Noll [9], defined the natural time in terms of the viscometric functions and remarked that its magnitude is actually a measure of the relative importance of normal stress effects, i.e.,the Weissenberg effects (see also Ref. [15]).

The Cauchy stress tensor T of the simple fluid is determined by the whole history of the deformation gradient F, i.e.,

The three viscometric functions for a simple fluid are defined as

In 1964, Truesdell [14] proposed to define the time function for a simple fluid of Noll [9] as follows

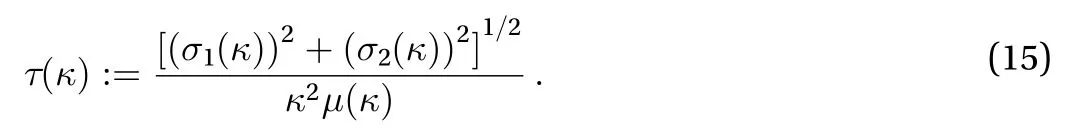
In addition, Truesdell [15] remarked that to calculate the natural time of a fluid one may in practice adoptinstead of(see also Ref. [28]). Hence, there follows

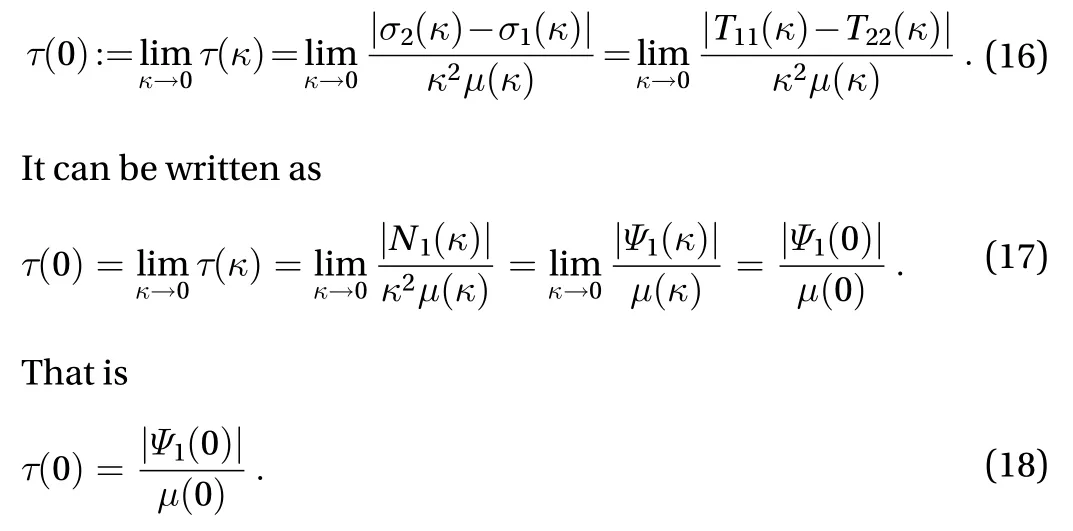
Equation (16) is another definition of the natural time, which is convenient for measurement in physical experiments; see Truesdell [15] and James [29]. Indeed, it is also adopted as a time constant in rheology to describe the fluid elasticity; see, for example, Boger [27], García-Franco [30]. Moreover, in their experimental investigation on the mixing of a visco-elastic fluid in twodimensional time-periodic flows, Niederkorn and Ottino [31]used the zero-shear-limit of the first (primary) normal stress difference to calculate the relaxation time of the fluidwhereis the viscosity.

Remark 1.The inelasticity of a Newtonian fluid can also be shown by making use of the notion of the natural time introduced by Truesdell [14]. By Eqs. (1)-(3), noting that in a viscometric flow,for a Newtonian fluid, each definition of the natural time, i.e., Eq. (15) or Eq. (16), givesThat is, the natural time of a Newtonian fluid is zero.

2.2 The natural time of turbulence of a Newtonian fluid

In homogeneous turbulent shear flow, the mean velocity field in a rectangular Cartesian coordinate system is given by

It is obvious that the mean velocity field of homogeneous turbulent shear flow is kinematically similar to the velocity field of the simple shearing flow of a simple fluid investigated by Truesdell [14], and by Coleman et al. [32]. Moreover, similar to the Cauchy stress in simple shearing flow, in homogeneous turbulent shear flow, each component of the Reynolds stress tensoris simply a function of the mean shear rateand time

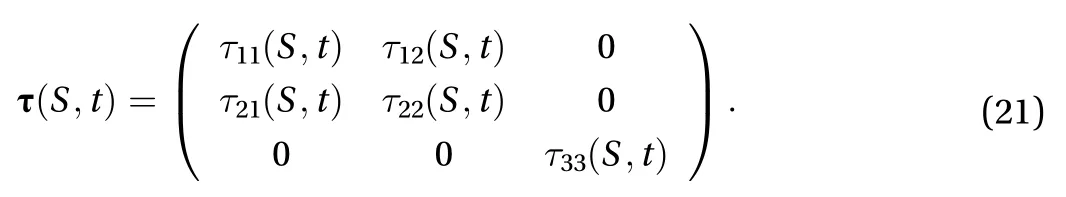
The three turbulent viscometric functions in homogeneous turbulent shear flow are defined as follows; see Huang et al. [13]:

In contrast to the natural time of a Newtonian fluid being zero, the natural time of a turbulent Newtonian fluid is non-zero,which can be shown by invoking the Reynolds stress transport equation. The natural time of turbulence is a measure of relative importance of the Reynolds normal stress effects, reflecting thus the elastic effect of the turbulence concerned.

Noting Eqs. (16)-(18), there follows from Eq. (22) the definition of the natural time of turbulence:

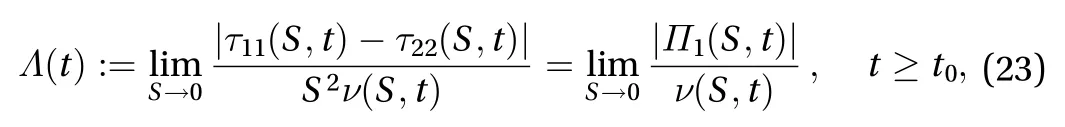
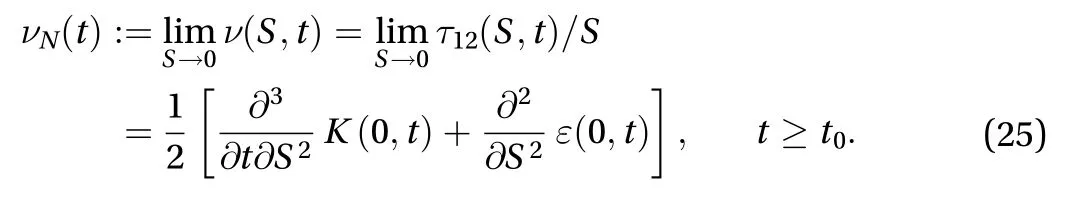
2.3 The evolution equation for the natural time of turbulence

In contrast to the constant natural times of some popular non-Newtonian fluids, e.g., the natural time of the fluid of gradeis a constant (see Truesdell [15]), the natural time of turbulencegiven by Eq. (23) is time-dependent and, physically,will gradually decrease with time like the natural viscosity of turbulence(see Huang et al. [13]), since in the limit of zero mean shear rate, the homogeneous turbulent shear flow becomes isotropic and starts to decay because of no driving force to sustain the turbulence.

In homogeneous turbulence, the Reynolds stress transport equation (10) reduces to

It follows from Eq. (26) that

.

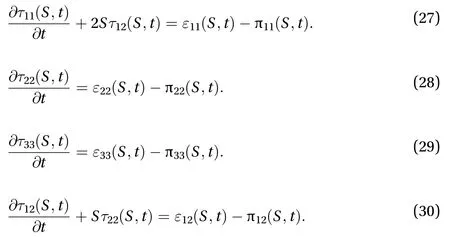
By Eqs. (27) and (28), we have

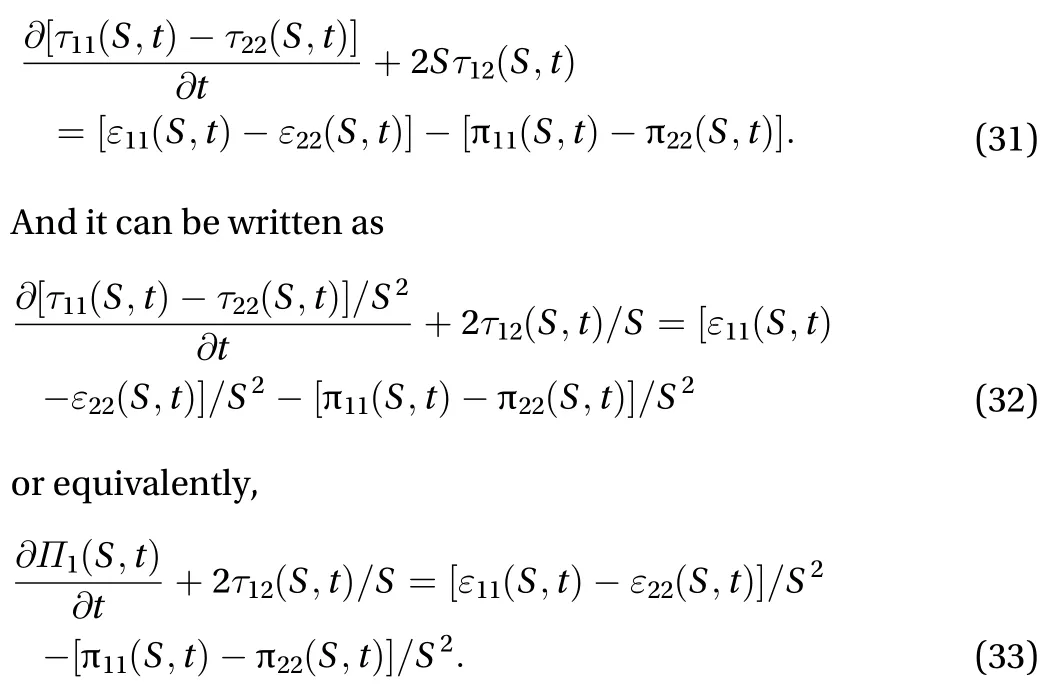
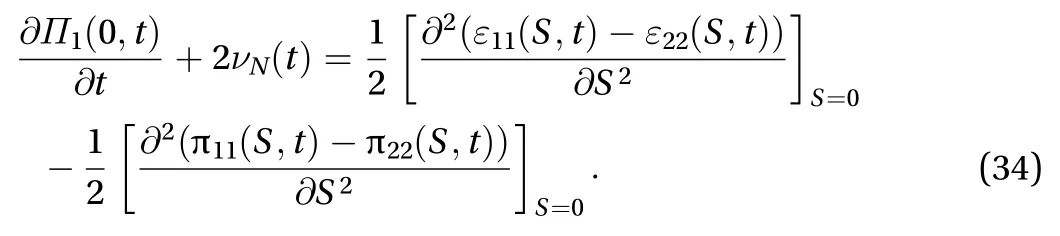
That is,

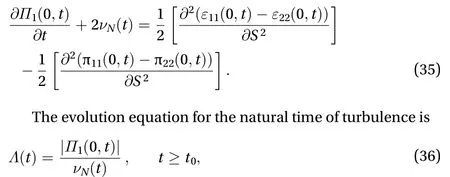
where the first Reynolds normal stress difference coefficient at zero mean shear rateis determined by Eq. (35) which contains the natural viscosity of turbulence.

In order to obtain an explicit expression for the natural time of turbulence, here we shall make use of the Launder et al.[21] basic model of the second-order closure to calculate. The Launder, Reece and Rodi basic model [21] includes both the model of Rotta [20] and the model for isotropization of production proposed by Naot et al. [33], and their pressure-strain correlation tensor takes the following form:

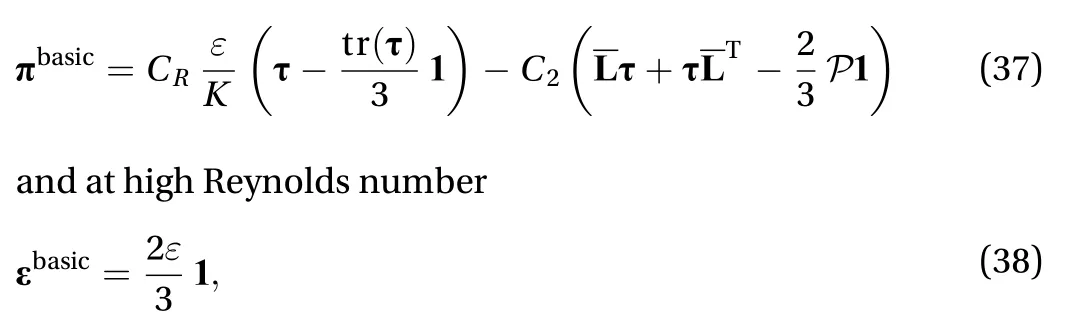
Substituting Eqs. (37) and (38) into Eq. (32) yields

By the experimental results of homogeneous turbulence (see Comte-Bellot and Corrsin [34] and Mohamed and LaRue [35]),we know that

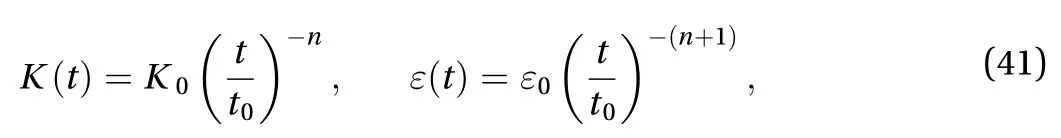
Recently, by employing the Launder, Reece and Rodi basic model [21] given by Eqs. (37) and (38), an explicit expression for the natural viscosity of turbulencehas been derived by Huang [36]:

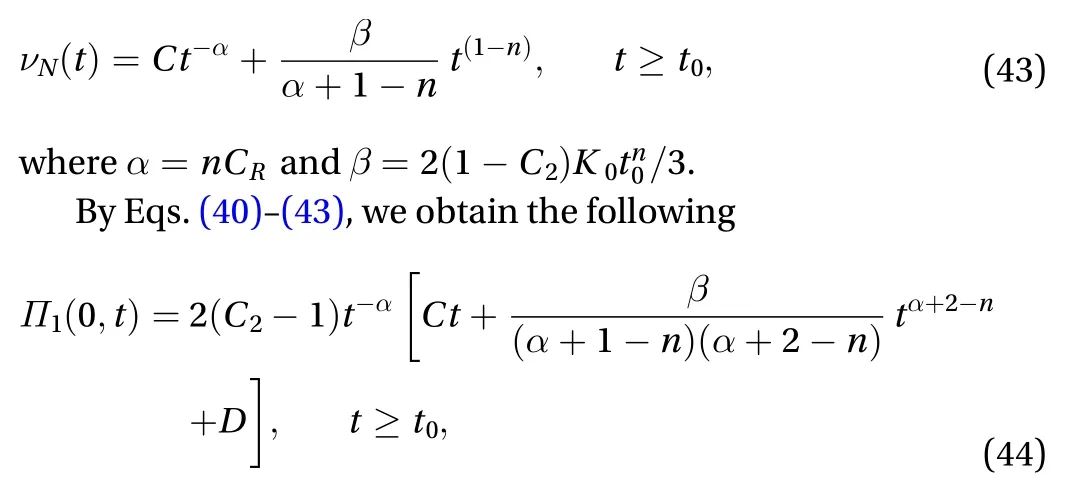
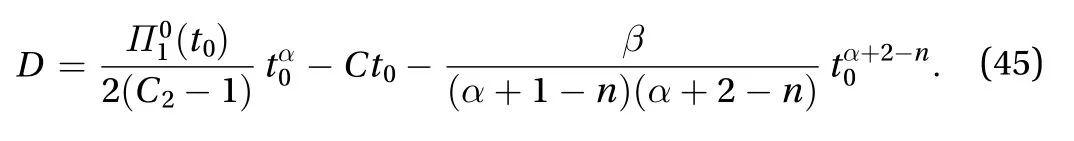
Of course, the natural viscosity of turbulence, as given by Eq. (25), and the first Reynolds normal stress difference coefficientgiven by Eq. (35) can be obtained by carrying out numerical simulations using the closure models of turbulence,the large eddy simulations, or the direct numerical simulations.

3 A general Weissenberg number that measures the elastic effects

Let us recall an insightful remark by Rivlin [4] on the normal stress effects of a turbulent Newtonian fluid: “It has been noted that the fluids in which the normal stress effects have been observed are visco-elastic and this suggests that turbulent Newtonian fluids may similarly show some elastic effects under suitable experimental conditions. The eddies in a turbulent Newtonian fluid will presumably undergo preferential orientation when the turbulent fluid is sheared, providing a possible mechanism for the effects in the turbulent fluid.” In what follows, we shall introduce three Weissenberg numbers of turbulence to characterize the elastic effects of the turbulence of a Newtonian fluid.

Boger [27] pointed out that the elastic effects in flows of visco-elastic fluids are generally characterized by one dimensionless number, the Weissenberg numberwhereis the relaxation time of the fluid andis the shear rate. The Maxwell fluid and the Oldroyd-B fluid represent constant-viscosity elastic liquids (see Stokes et al. [37]). In contrast to these fluids whose constitutive equations are explicitly given, in turbulent flows the Reynolds stress transport equation is not closed and must be modelled before any calculations to be performed. As we shall see, the natural time of turbulence derived from the Reynolds stress transport equation in homogeneous turbulent shear flow plays a similar role as does the relaxation time of a visco-elastic fluid and, in particular, it can be used to define a dimensionless number, called the natural Weissenberg number of turbulence.

3.1 The natural Weissenberg number of turbulence

Now in terms of the natural time of turbulence, which is closely related to the natural viscosity of turbulenceas seen in Eq. (36), accordingly, we can define the natural Weissenberg number for homogeneous turbulent shear flow as follows:

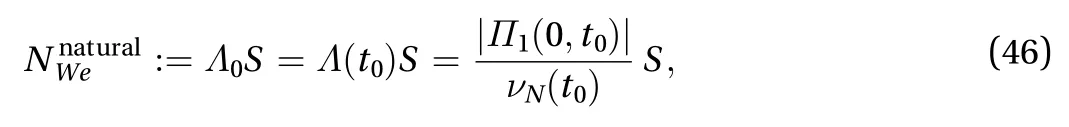
Remark 2. For homogeneous turbulence, the natural Weissenberg number of turbulence takes the form,whereIt reduces to Eq. (46) in homogeneous turbulent shear flow, for which,being the mean shear rate. In order to investigate the normal stress effects of a turbulent flow in general, say, a wall-bounded turbulent flow, we must take into account the physical facts that, on the solid boundary, the Reynolds stress tensorbecomesdue to no-slip boundary condition, whereas the mean Cauchy stress tensorplays a dominant role there in near-wall turbulence.

3.2 The primary Weissenberg number of turbulence

We define the primary Weissenberg number of turbulence as follows, which is in keeping with the Weissenberg number used in rheology that is defined as the ratio of the first (primary) normal stress difference to the shear stress:since the mean Cauchy shear stressis negligibly small compared to the turbulent shear stress(Reynolds shear stress). In fact, in wall-bounded turbulent flows, generally, the greater is the distance from the boundary, the smaller become the mean Cauchy shear stresses. Of course, there exists no boundary in homogeneous turbulent shear flow.

In laminar flow, Eq. (47) reduces to which is the Weissenberg number used in rheology to investigate the elastic effects of visco-elastic fluids; see, for example, Boger[27], Astarita [28], Niederkorn and Ottino [31], Harnoy [38], and Meulenbroek et al. [39].

The above results indicate that the primary Weissenberg number of turbulenceagreeswith the naturalWeissenberg number of turbulence, showing thatthe homogeneous turbulent shear flow becomes more and more elastic as the mean shear rateincreases. Here, it should be noted that the natural Weissenberg number of turbulenceholds for homogeneous turbulence only, not applicable to general turbulent flows because it does not involve the contributions of the mean Cauchy stresses that play a significant role in near-wall turbulent boundary layers.

3.3 The general Weissenberg number of turbulence

Noting that there are all sorts of boundaries in an enormous variety of complex turbulent flows, thus, in general three-dimensional turbulence, in contrast to the primary Weissenberg numberwhich involves only thefirst normal stress differenceand the shearstress, we must consider the contributions to the elastic effects due to all the normal stress differences, i.e.,,and, as a whole a nd, at the same time, the contributions ofall theshearstresses,i.e.,,and,must beaccounted for.

Hence, here we put forth the following general Weissenberg number to characterize the elastic effects of turbulence in general:

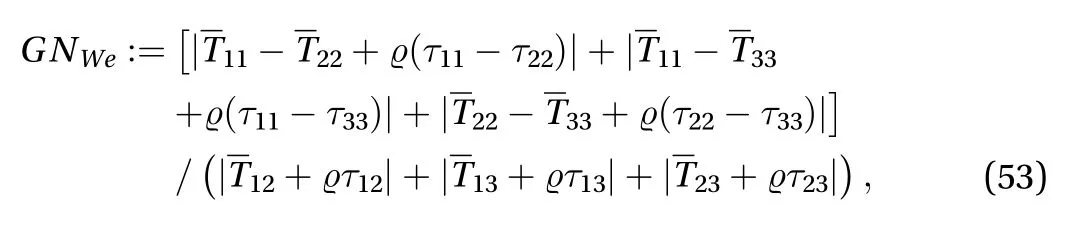
which is the ratio of all the elastic to viscous forces in the turbulent fluid.

We should pay close attention to Eq. (53) for any spacial pointat which

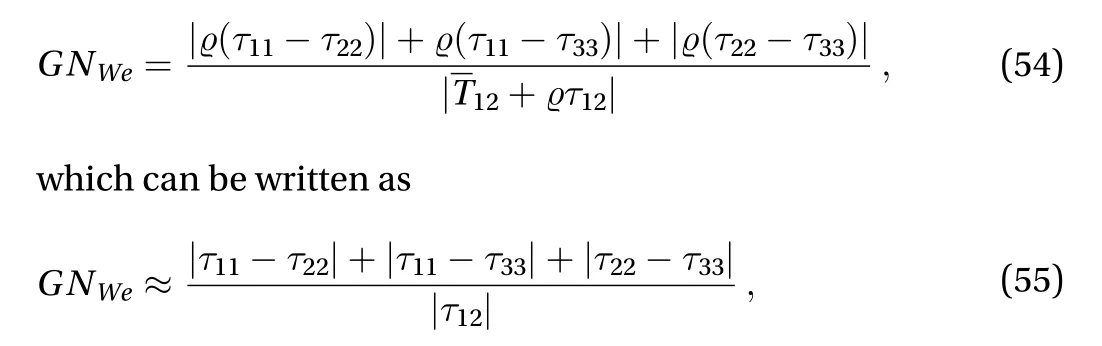
In homogeneous turbulent shear flow, Eq. (53) reduces to since in this case the mean Cauchy shear stressis negligibly small in comparison to the Reynolds shear stress.

Now let us re-examine the previously studied cases of (a), (b)and (c) with the general Weissenberg number of turbulencenoting that here

By the general Weissenberg number of turbulence,again, we see that the homogeneous turbulent shear flow becomes more and more elastic with the increasing mean shear rate, confirming from a general perspective what have been shown earlier by using the natural Weissenberg number of turbulenceand the primary Weissenberg number of turbulence, respectively.

Remark 3.Regarding the normal stress effects, it is generally believed that the Weissenberg effect shown by polymer solutions is usually explained by supposing that the elements of the stress tensor are no longer independent, namely, a shear stress can give rise to normal stresses that causes the anomalous,visco-elastic effect; see, for example, Rivlin [4], and Lumley [26].By contrast, the case of turbulence appears to be much more intriguing and complicated, but no such a similar assumption as mentioned for visco-elastic fluids would be necessary for the turbulence of a Newtonian fluid. In fact, even in homogeneous turbulent shear flow, that the Reynolds normal stressis germane to the Reynolds shear stresscan be clearly seen from Eq. (31), which is derived from the Reynolds stress transport equation that, of course, is not closed unless is modelled.

3.4 The general Weissenberg number of turbulence: Its application in fully developed turbulent channel flow

Now let us examine the case of fully developed turbulent channel flow: its mean velocity field is given by and the mean velocity gradient.

According to the direct numerical simulation (DNS) data of Kim et al. [41]for fully developed turbulent channel flow wherenoting thatandwe havecase (e): at the wall,,whereas the Reynolds stresstensor.Hence,by Eq. (53),the general Weissenberg number of turbulence

which shows that there is no elastic effect at the wall for the fully developed turbulent channel flow of a Newtonian fluid;case (f): atwhere the peak production takes place,, the general Weissenberg number of turbulence here

This indicates that in fully developed turbulent channel flow,the elastic effect reaches its maximum,at the centerline with the inequality of the Reynolds normal stresses—that is, the unequalandcompletely dominate the turbulent fluid therein, whereas the mean Cauchy and Reynolds shear stresses become zero. In other words, the fully developed turbulent channel flow of an incompressible Newtonian fluid behaves like a visco-elastic fluid, exhibiting both viscous and elastic effects—indeed, on the boundary, itshows viscous effect() butno elastic effect(), and the elastic effect at the point of peak production is about three times the elastic effect at the point in the log-law region, whereas at the centerline, itispurely elastic (),involving no viscous shearing at all (, thus.

In complex flows of visco-elastic fluids, it is not uncommon that the Weissenberg number can be very large, which refers to the highly elastic fluid limit, as shown, for example, by Azaiez and Homsy [42] and Renardy [43], or even infinite, e.g., at the reentrant corner of contraction flow of an upper-convected Maxwell fluid (see Renardy [44]) and in plane parallel visco-elastic shear flows, as investigated by Kaffel and Renardy [45].

Remark 4.In fully developed turbulent channel flow of a Newtonian fluid, the general Weissenberg number of turbulenceis zero at the wall of the channel, showing no elastic effect therein. However, a visco-elastic fluid generally exhibits elastic effect at the solid wall. For example, in the Poiseuille flow of an Oldroyd-B fluid, the Weissenberg number, whereis the maximum velocity of its parabolic profile,is the relaxation time of the Oldroyd-B fluid, andis the radius of the pipe, as shown by Meulenbroek et al. [39].

3.5 The general Weissenberg number as a measure of the elastic effects of non-Newtonian fluids

In laminar flow, the general Weissenberg number of turbulence defined by Eq. (53) reduces to

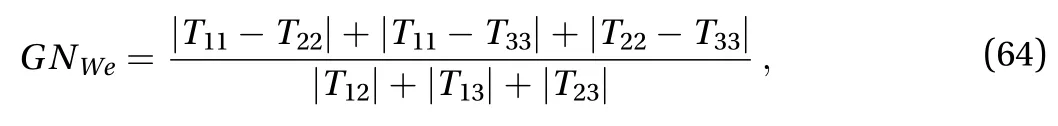
which is the expression that applies to the investigation of the elastic effects of non-Newtonian fluids; in contrast to, it includes the contribution of the second normal stress difference,of which the measurement had been performed long time ago by Keentok et al. [46] among others, and that of the third normal stress difference.

For illustration, let us study the case of a steady laminar channel flow, of which the velocity field is given by

Consider an incompressible fluid of grade 2, for which the Cauchy stress tensor reads

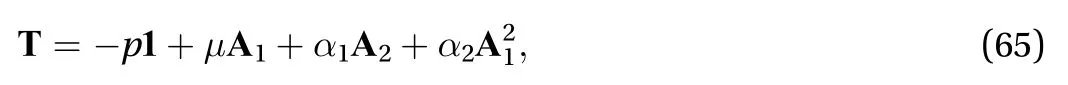
It is straightforward to show that, in this case, the general Weissenberg number is

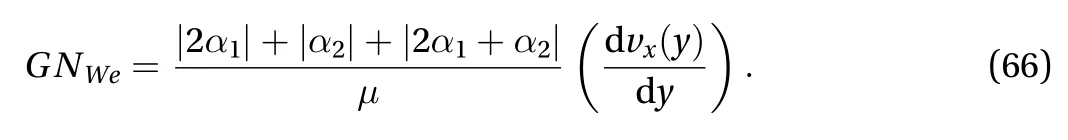
Besides, if we use the primary Weissenberg numberinstead to calculate the elastic effect, i.e.,neglecting the contributions ofand, which correspond to the terms ofandin, we simply get

Moreover, at the centerline of the channel, due to the symmetry of the velocity

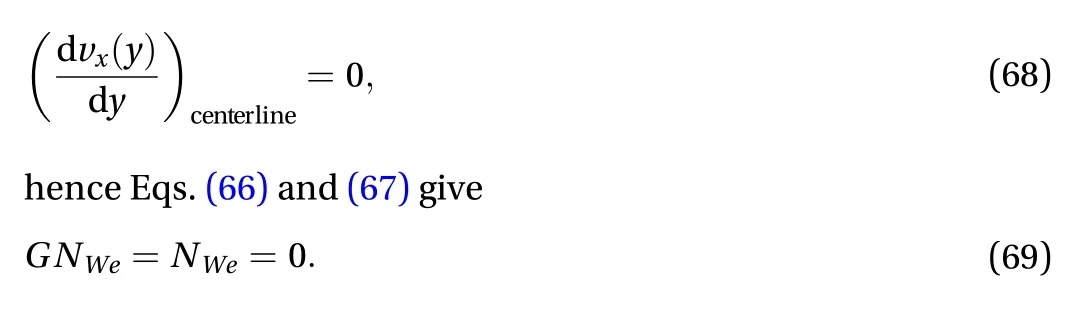
That is, there is no elastic effect at the centerline for the fluid of grade 2, contrasting sharply with the fully developed turbulent channel flow of a Newtonian fluid as shown by Eq. (63).

On comparing Eq. (66) with Eq. (67), we see that the general Weissenberg numbercanbetter describe the overall elastic effects than does the primaryWeissenberg numbersincefor a fluidof grade 2, in general,Here, it should be noted that the Cauchy stress tensor for a Reiner-Rivlin fluidwhereandare material constants; hence, the corresponding results in laminar channel flow are readily obtained by setting,andin Eq. (65).

The above analysis indicates that, in laminar channel flow,the general Weissenberg numberprovides an overall measure of the elastic effects caused by the whole normal stress differences, noting that many complex phenomena of non-Newtonian fluids can be characterized by the normal stress differences, as shown, for example, by James [29], Boger [47], Bird and Wiest [48].

Indeed, in their study on the purely elastic instability in Taylor-Couette flow of visco-elastic fluids, Larson et al. [49] reported that the mechanism of the visco-elastic instabilities of Taylor-Couette flow bears some similarity to that which produces rod-climbing phenomenon, i.e., the Weissenberg effect,and the driving force for the instability is the interaction between the velocity fluctuation and the first (primary) stress difference in the base flow. Groisman and Steinberg [50] investigated experimentally the elastic turbulence in a polymer solution flow,showing that the turbulent flow of the polymeric fluid is completely characterized by the Weissenberg number,meanwhile, the Reynolds number Re is negligibly small, in striking contrast to the turbulent flow of a Newtonian fluid that is characterized by the large Reynolds number. Besides, Larson [51]pointed out that the so-called “elastic turbulence” of viscous polymeric fluids actually hasnothing to dowiththe inertia, since the Reynoldsnumber Re can be aslow as, but it is characterized by the Weissenberg number, the ratio of elastic to viscous forces in the fluids.

Remark 5.In fully developed homogeneous turbulent shear flow, the natural Weissenberg number of turbulence, whereis the natural time of turbulence (in certain sense, the relaxation time of the turbulence) andis the mean shear rate, is very much like the Weissenberg numberfor the elastic turbulence of a polymeric fluid studied by Groisman and Steinberg [50], whereis the relaxation time of the fluid andis the shear rate. Thus, the elasticity of both turbulent flows is actually described by the two Weissenberg numbers very much alike, respectively—however, the turbulence of a Newtonian fluid is characterized by the Reynolds number, which manifests the vital role the inertia plays in the development of turbulence, whereas, interestingly, the elastic turbulence of a polymeric fluid, which is characterized by the Weissenberg number, can occur without inertia.

4 Concluding remarks

Motivated by the seminal work of Weissenberg [1], Poynting[2], Truesdell [3, 14], Rivlin [4], Coleman et al. [32], in this work we have introduced the natural time of turbulence of a Newtonian fluid and the corresponding natural Weissenberg number of turbulence. We have defined the primary Weissenberg number of turbulence, which in laminar flow reduces to the Weissenberg number used in rheology to characterize the elasticity of non-Newtonian fluids. Furthermore, we have put forth a general Weissenberg number of turbulenceto measure the overall elastic effects of turbulence, which includes as a special case the primary Weissenberg number of turbulence, and, besides, can be used to describe the elastic effects of non-Newtonian fluids in laminar flow. The experimental data of Tavoularis and Karnik [40] for homogeneous turbulent shear flow and the DNS data obtained by Kim et al. [41] for fully developed turbulent channel flow have been used to analyze the elastic effects of turbulence by employing the Weissenberg numbers of turbulence introduced in the present paper.

As far as the experimental work is concerned, measurements of the initial value of the natural time of turbulenceand the one of the natural viscosity of turbulenceneed to be made in homogeneous turbulent shear flow. Truesdell [14] mentioned that it was not an easy task to accurately measure the natural time of a non-Newtonian fluid, citing Markovitz's experiments using solutions of polyisobutylene in a viscometric flow. It appears to be much more challenging to perform experiments to measure the natural time and natural viscosity of turbulence,noticing that Markovitz's experiments were performed in laminar flow of a non-Newtonian fluid. Therefore, extrapolation may likely be adopted to determine the natural viscosity and natural time of turbulence as the mean shear rateapproaches zero.Moreover, given the initial values ofandthat are expected to be obtained by experiments, naturally, it will be worth performing the large eddy simulations, the numerical simulations based on turbulence closure models, or the direct numerical simulations of the evolution of the natural viscosity of turbulenceand of the natural time of turbulence, as the numerical simulation may provide a feasible means to overcome the difficulties often encountered in conducting the physical experiments. It should be noted that it is impossible to derive the natural time of turbulence on the basis of the Reynolds stress transport equation without the natural viscosity of turbulence, as clearly shown by Eqs. (35) and (36).

Over the past thirty years, a large number of researches have been carried out to investigate the instabilities in visco-elastic flows employing the Weissenberg number; see, for example,Joseph [52] investigating the instability associated with a change of type characterized by the Weissenberg number, Larson [53]addressing the flow instabilities caused by the normal stress differences, Renardy [44] on dealing with the high Weissenberg number boundary layer that leads to a sharp transition in the behavior of the Cauchy stresses near the wall as studied, e.g., by Hagen and Renardy [54], the purely elastic instability in shear flows associated with the normal stress differences that occur at nearly zero Reynolds number, and the visco-elastic Bénard problem, to mention a few. In addition, for recently published researches that are closely related to the normal stress differences in oscillatory shear flows of a number of typical viscoelastic fluids, we refer the reader to the work of Giacomin and Bird [55], Saengow and Giacomin [56]; see also Ref. [57].

Noticing the near-wall high-shear layer that occurs in transition in wall-bounded flows of a Newtonian fluid reported in a comprehensive review by Lee and Wu [58], which bears an interesting analogy to the bounded flows of visco-elastic fluids associated with the inequality of the normal stresses, and the recent research conducted by Zhu et al. [59] on the instability evolution that appears in the transitional boundary layer and its impact on the aerodynamic heating, it will be of interest to use the general Weissenberg number of turbulence, together with the approach of numerical simulation, to investigate the elastic effects of the laminar-to-turbulent transition from the perspective of the normal stress differences under shearing, namely, the Weissenberg effect.