Direct method for a Cauchy problem with application to a Tokamak

Mohsen Tadi

Mechanical Engineering Department, Univerisity of Colorado Denver, Denver, CO 80204, USA

Keywords:Cauchy problem Moment problem Non-iterative Tokamak

A B S T R A C T This note is concerned with a new direct (non-iterative) method for the solution of an elliptic inverse problem. This method is based on the application of the Green's second identity which leads to a moment problem for the unknown boundary condition. Tikhonov regularization is used to obtain a stable and close approximation of the missing boundary condition without any need for iterations. Four examples are used to study the applicability of the method with the presence of noise.

In this note, we introduce a direct (non-iterative) method for the solution of a particular ill-posed elliptic inverse problem.This problem falls within the general area of inverse problems that have numerous applications in various fields of engineering[1, 2]. The specific problem studied in this note is the case of a steady-state heat conduction problem within a ring, where no information on the interior boundary is available. A similar situation arises in a Tokamak where the internal boundary of the poloidal flux is unknown [3].

The literature on this problem is vast [4] (and references there in). Recent results on this particular problem includes a meshless method [5], singular boundary method [6], discrete Fourier transform method [7], and a method based on proper solution space [8].

The purpose of this letter is to develop a direct (non-iterative) method for an inverse problem for annular domains. Analytical issues for this problem has been addressed [9], with particular application to a Tokamak with a circular cross-section [3]. Iterative methods for this particular application in fusion research has been developed [10, 11] (also references there in). However,fast direct (non-iterative) solution methods are more suitable. In addition, results in this letter apply to non-circular boundaries.

Notation:The domain is a ringwith outer radiusand inner radius. We useto denote the outer boundary andto denote the inner boundary. We useto denote the dummy variable when the integration is performed over the outer boundary, i.e.,, andwhen the integration is performed over the inner boundary, i.e.,. We use bold letters to denote vectors and matrices.

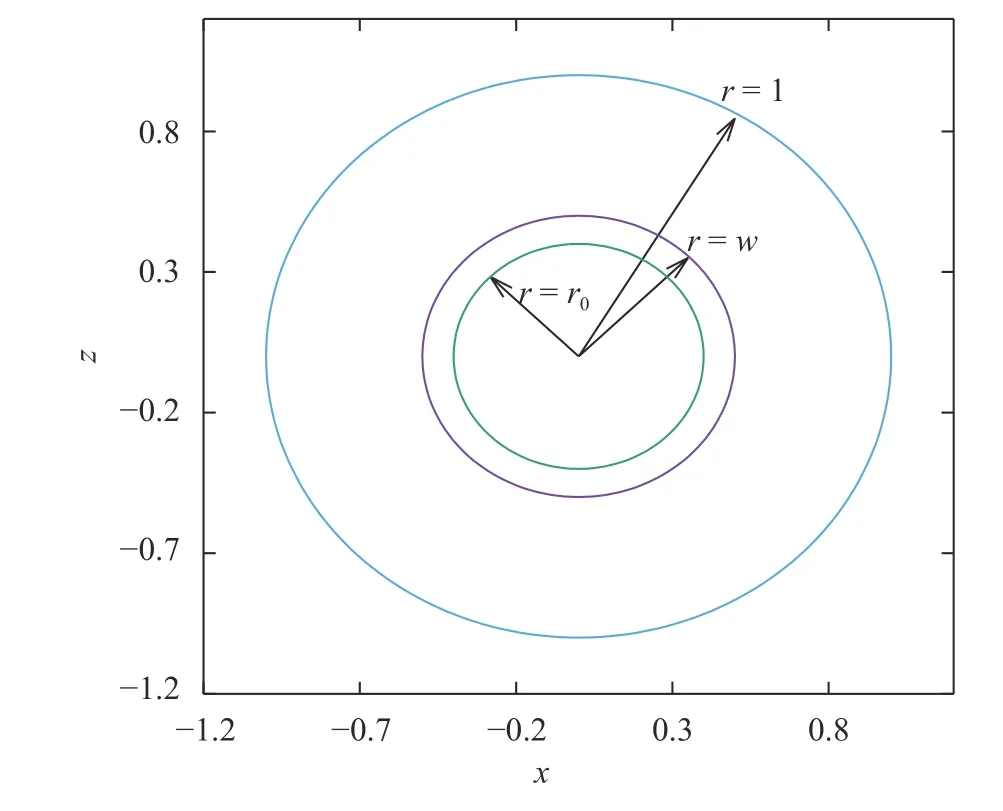
Fig. 1. Two-dimensional domain under study

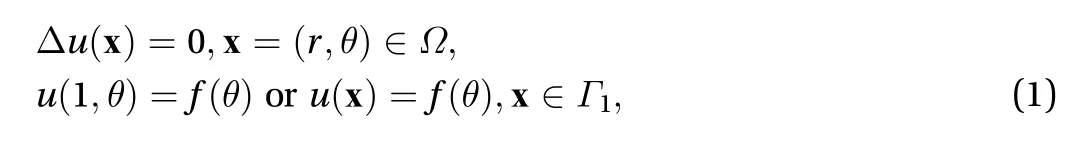
and assume that the outer boundary, i.e., is accessible and can be used to collect data. Measurements in the form of flux can be collected and provided according to

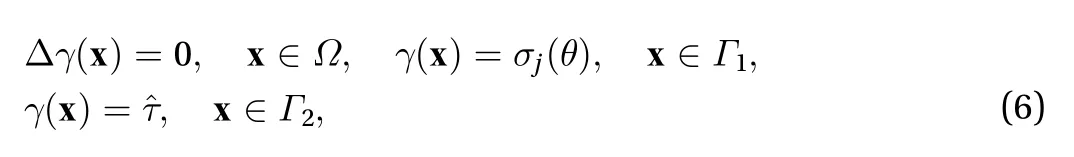
Note that in the second under braced term in the above equation, we have used the boundary condition.Subtracting Eq. (8) from Eq. (5) leads to

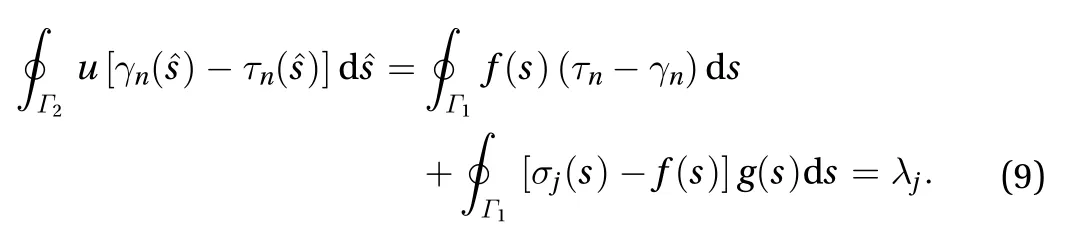
The above equation is a moment problem [12] for the unknown boundary condition. The quantities on the right-handside are either known or can be computed and we are denoting them with. By choosing linearly independentfunctions,we can generate a series of moment problems given by

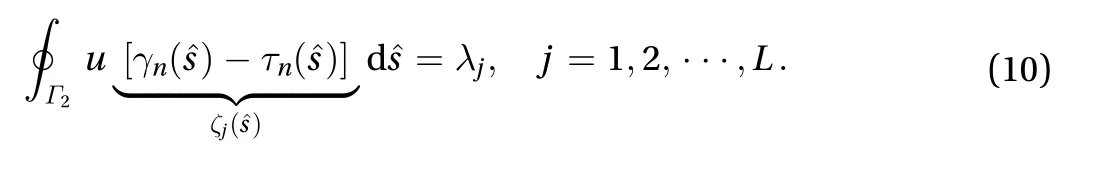
Assuming an expansion for the unknown boundary conditionaccording to, Eq. (10) leads to a non-square linear system given by

where the unknown coefficientsare placed in the vectorand the known right-hand side entriesare placed in the vector.The above system can be solved after introducing Tikhonov regularization which puts a bound on the slope of the unknown function. We next prove that the functions in the above kernel are linearly independent.

Theorem 1:If the functionsandare linearly independent then the functionsandare also linearly independent.

Proof:Since there isonly one, it issufficienttoshow that thefunctionsandare linearly independent.The two Dirichlet problems are given by

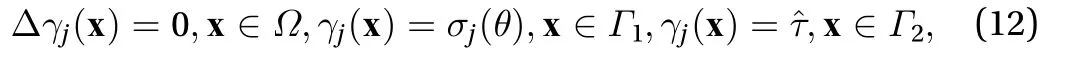
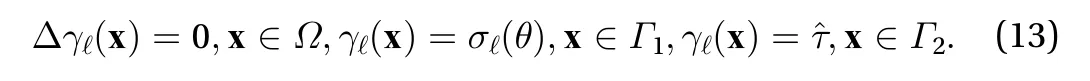
To simplify it further, we can subtract a background field given by

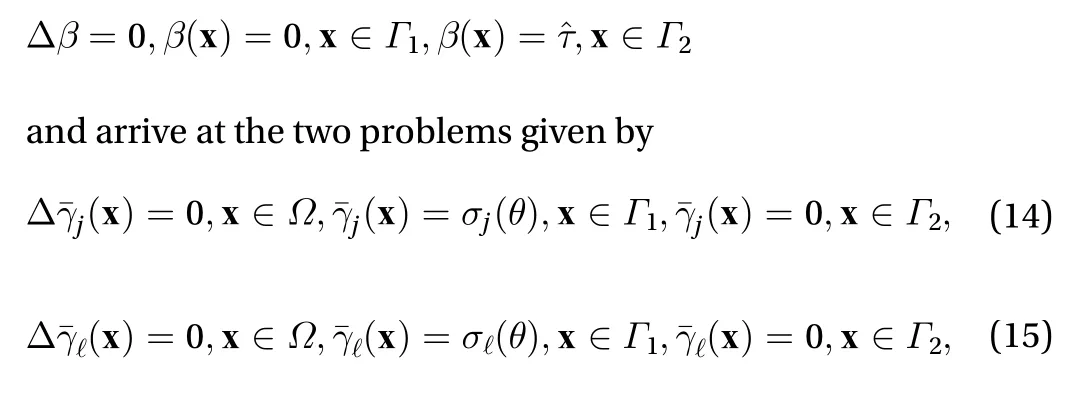
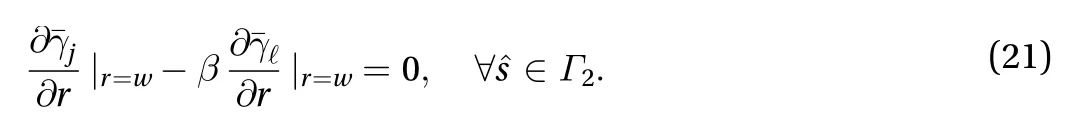
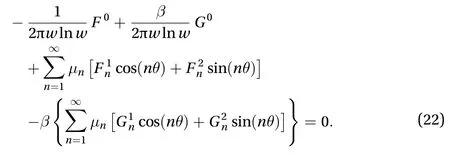
We can follow the similar steps used in the derivation of the Fourier series coefficients and obtain three different equations.(1) We can integrate the above equation over the domain,(2) multiply the equation byand integrate over the domain, and (3) multiply the equation byand integrate over the domain. After using the simplifications in Eqs. (18)-(20) and simplifying, it leads to

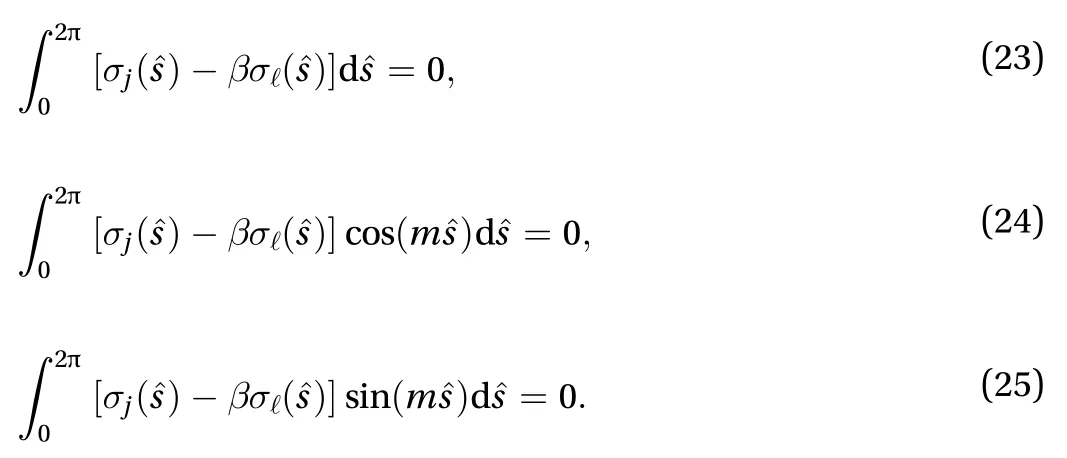
If one considers the Fourier representation of the functionthe above three equations leads to

which is a contradiction.

Remark 1:For more than two sampling functions,can follow a similar approach and arrive at a similar equation which leads to contradiction. We next present the details by considering two specific examples.

Example 1:Consider the elliptic system given in Eq. (1) and assume that the external boundary condition is given by. The problem is to recover the temperature at the interior boundary which is located at. One can choosesampling functions that are denoted by. Dividing thedirection intoequal intervals leads to, and dividing the radial direction intoequal intervals leads to. To generate the sampling functions, we use a combination of cubic B-spines and sine functions. We essentially need smooth linearly independent functions that satisfy the periodic boundary condition of the problem. Cubic B-splines have four intervals and are given [14,15]

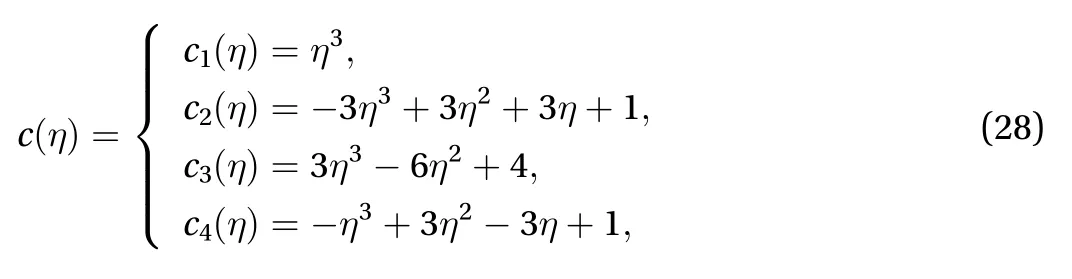
It also shows the singular values of the coefficient matrixfor. For larger number of sampling points little improvement in the number of nonzero singular values of the matrixis obtained1.

There are about 23 good eigenvalues out of 28, which is a characteristic of a moment problem. In order to be able to invert the matrix, we need to introduce regularization by imposing a bound on the slope of the recovered function. We also need to require that the recovered function be periodic2. We can impose that the recovered function be continuous by requiring that

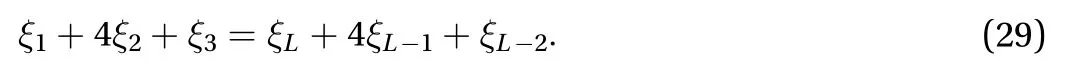
Therefore instead of Eq. (11), we proceed to solve a leastsquare problem given by

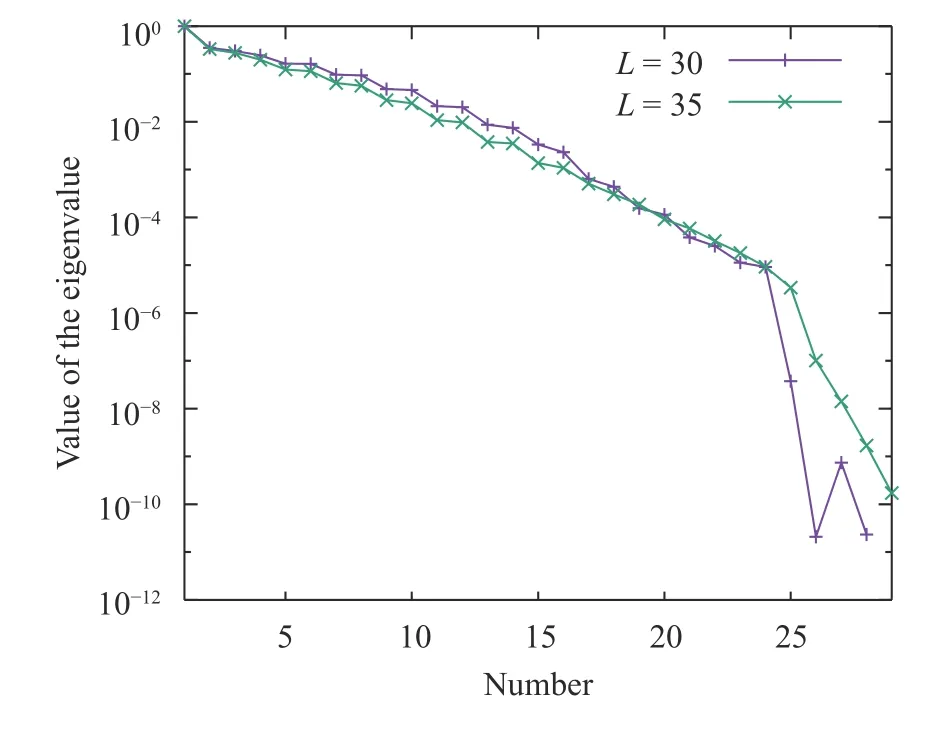
Fig. 2. Normalized eigenvalues of the coefficient matrix in Eq. (11)

Example 2:We next consider the same Cauchy problem and study the effect of noise. We can set the parameterand keep the rest of the parameters the same as their values in example 1. The exact value of the boundary condition is given by

Figure 4 compares the recovered functions for various levels of noise. The method can recover a very close estimate of the unknown boundary condition directly for various levels of noise.Another feature of the method presented here is that, it is able to recover a close estimate of unknown boundary conditions where the unknown functions have regions with large gradients without iterations.

Figure 5 presents the basic geometry of a Tokamak. Figure 6 depicts a cross-section of the Tokamak. The plasma is confined

Fig. 3. Recovered unknown interior boundary for example 1 with 0.04% noise

Fig. 4. Recovered unknown temperature for example 2 with different noise levels

1In addition, for larger values of, cubic-B splines have larger gradients and finner mesh is required for accurate numerical calculations.2Using cubic B-splines, we can enforce the recovered function to be, but here, we are only enforcing that the function be continuous.within the poloidal flux which acts as a buffer between the plasma and the boundary. The location of this boundaryis not precisely known. The external boundary of the poloidal flux is the actual physical boundary of the Tokamak, which is accessible and can be used for measurements. Here, we can extend the domain and obtain the value of the poloiodal flux at an imaginary internal boundary as shown in Fig. 6 which is a circle with a constant radius. Poloidal flux attains it's highest value at the unknown boundary. In order to locate the boundary of the plasma (i.e.,), we can obtain the value of the poloidal flux at the imaginary boundary (), and interpolate for the location of the boundary. We used this approach in Ref. [11].However, we used an iterative method to recover the flux distribution at the imaginary boundary. Here, we only apply the present direct method to recover the flux at the boundary. The elliptic equation for the poloidal fluxin vacuum is given by

where the differential operatoris defined.We are also using the physical dimensions close to what is reported in Ref. [10], i.e., and radius of the cross-section 1.

Fig. 5. Toroidal geometry of the Tokamak Tore Supra

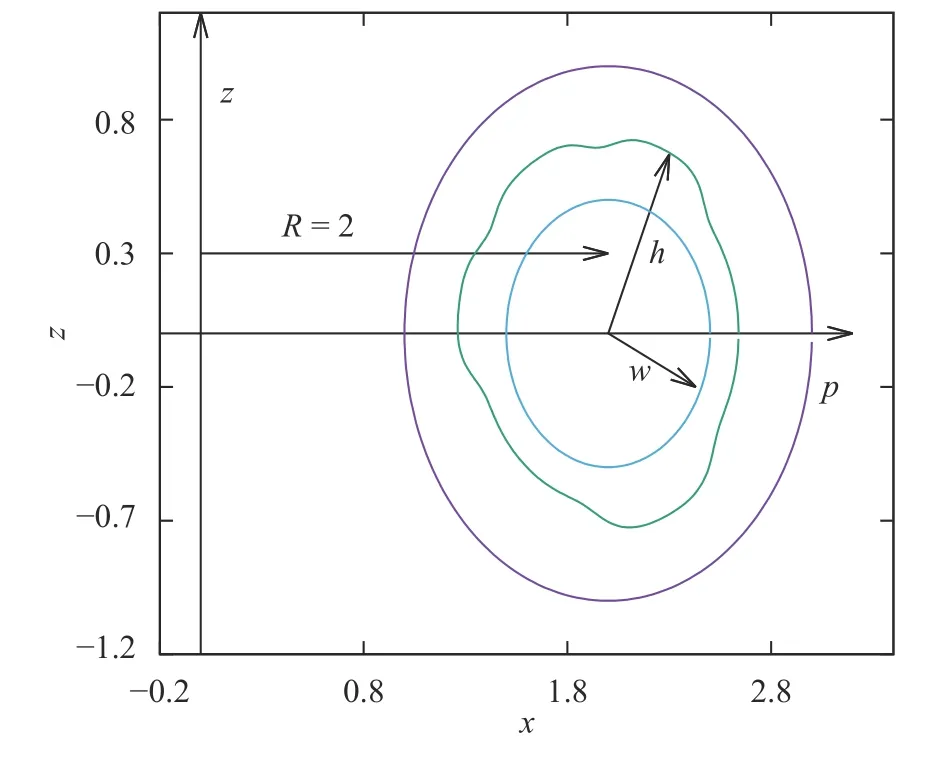
Fig. 6. Cross section of the Tokamak

Expanding the equation leads to

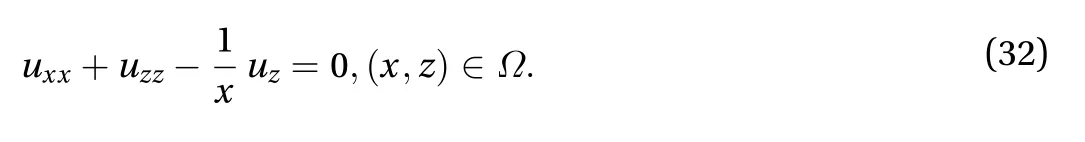
The boundary conditions forcan also be computed according to. We can considerthe elliptic problem given by

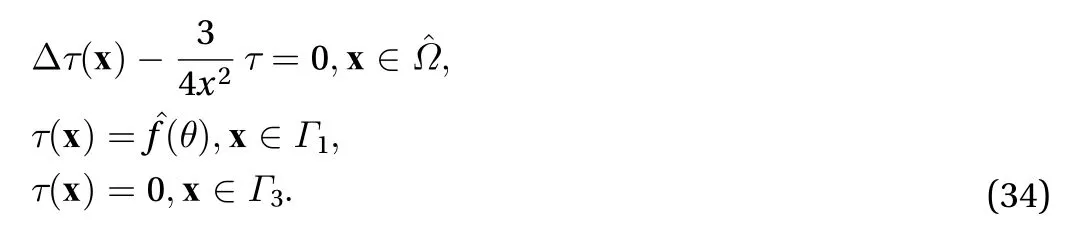
This is similar to Eq. (3), with the same domain. The boundary condition atis given by

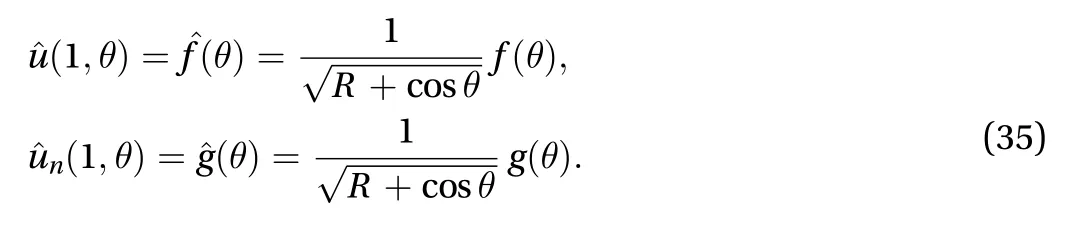
Applying the Green's second identity toandsimilar to Eq. (4)leads to a zero on the left-hand-side which is similar to Eq. (5).We next consider the elliptic system given by

which is similar to Eq. (6). Applying the Green's second identity leads to a zero on the right-hand-side similar to Eq. (8). We can then proceed in a similar way and arrive at a moment problem similar to Eq. (11). We next consider a numerical example.

Example 3:We next consider the same Cauchy problem for the poloidal flux given in Eq. (31). Assume that the external boundary condition is given by

Example 4:We next consider the same Cauchy problem studied is example 3 with% noise. Figure 8 presents the recovered value of the poloidal flux at the interior boundary with three different values of. We are using cubic-B splines, which are suitable for approximating a general function with few basis elements.

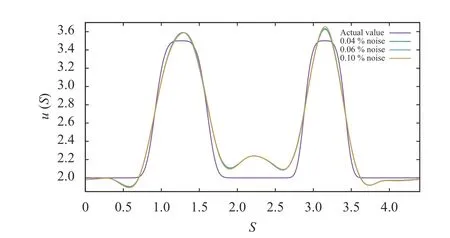
Fig. 7. Recovered unknown interior boundary at for the example 3

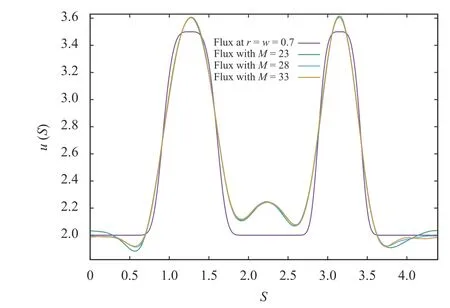
Fig. 8. Recovered poloidal flux at for the example 4

In this note we presented a non-iterative (direct) method for a specific Cauchy problem. This method is based on the application of the Green's second identity and leads to a moment problem. It is particularly useful for applications in Tokamak where direct (non-iterative) methods are needed. It also shows good robustness to noise.