Pendulum systems for harvesting vibration energy from railroad tracks and sleepers during the passage of a high-speed train: A feasibility evaluation

Franco E. Dotti*, Mauricio D. Sosa

a Grupo de Investigación en Multifísica Aplicada, Universidad Tecnológica Nacional, Facultad Regional Bahía Blanca. Consejo Nacional de Investigaciones Científicas y Técnicas. Argentina b Grupo de Investigación en Multifísica Aplicada, Universidad Tecnológica Nacional, Facultad Regional Bahía Blanca. Argentina

Keywords:Energy harvesting Parametric pendulum Railroad safety Train induced vibration

A B S T R A C T We evaluate the feasibility of recovering energy from the vibrations of track and sleepers, during passage of a high-speed train, by means of a pendulum harvester. A simple mathematical model of the parametric pendulum is employed to obtain numerical predictions, while measured data of vibration tests during the passage of a Thalys high-speed train are considered as input forcing.Since a sustained rotation is the most energetic motion of a pendulum, the possibility of achieving such state is evaluated, taking into account the influence of initial conditions, damping and other factors. Numerical simulations show that rotating pendulum harvesters with sufficiently low viscous damping could be able to generate a usable average power on the order of 5-6 W per unit.Considering a modular arrangement of devices, such energy is enough to feed variety of rail-side equipment, as wireless sensors or warning light systems. However, a suitable choice of initial conditions could be a difficult task, leading to the need of a control action.

Unprotected railroad crossings and derailments due to mechanical failures represent the two most significant sources of railroad accidents all over the world [1, 2]. In order to improve safety, warning light systems and structural health monitoring(SHM) sensors are strictly necessary. But in remote areas, the lack of electrical infrastructure represents a major impediment for the installation of rail-side equipment.

A potential solution to this problem is given by the use of autonomous systems, powered by energy harvested from vibrations of the track and/or sleepers caused by passing trains. The vibration of the track constitutes a time-limited excitation, since the motion is only significant for a short period of time. For high speed trains (HST), a typical duration of track vibration is on the order of 3-5 s [3, 4]. Despite their short duration, these vibrations can be highly energetic. Thus, several technologies have been developed and tested aiming to scavenge that energy, being the most common devices piezoelectric [5, 6], electromagnetic [7] and mechanical [8-11]. An interesting comparison among several devices can be found in Ref. [1]. Piezoelectric and inductive voice coil devices were reported to generate an average power on the order of 4-12 mW [5], which is enough to energize SHM sensors. To feed systems with higher power demands,as warning lights at grade crossings, an average power on the order of 10 W is required [1]. Mechanical devices have been considered in such situation, being rack and pinion [9], hydraulic[10] and cam-based [11] the most employed devices.

The vertical parametric pendulum was firstly proposed as an energy harvester by Prof. Marian Wiercigroch, aiming to extract energy from the ocean waves [12-15]. The idea is simple and intuitive: a pendulum vertically excited by an external motion at a given (averaged) frequency is able to achieve a rotational motion. Thus, a generator coupled to the pendulum axis could extract a part of that kinetic energy and produce electrical energy.In this article, we address the possibility of recovering energy during the passage of an HST by means of the same concept: a pendulum harvester attached to rails or sleepers. A simple mathematical model is employed to perform numerical simulations and evaluate the applicability of the concept. To ensure the existence of rotations, the physical dimensions of the harvester are defined in terms of the predominant excitation frequency in vertical direction, which is the fundamental bogie passage frequency [16]. The influence of initial conditions is evaluated, in order to avoid coexisting non rotating states as oscillating motion or chaos [14]. To count with realistic results, the input excitations correspond to experimental data measured during the passage of a Thalys HST [3].

A schematic diagram of a pendulum harvester is shown in Fig. 1. The pendulum consists of a bob of mass m and a rod of length l. The axis of the pendulum is mounted on a rigid frame,which is in turn fixed to a rigid base. The base is subjected to an external motion Y = Y(t), provided by the vibration of the track or sleeper. Besides, a generator coupled to the pendulum axis is able to extract a constant torque J from the pendulum motion.By means of Lagrange's equation for single degree-of-freedom non-conservative systems, the governing equation of such system can be expressed as

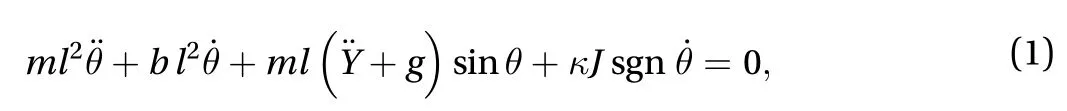
where tsthe time required by the pendulum to stop completely at its rest position and E0is the initial energy of the system, given by

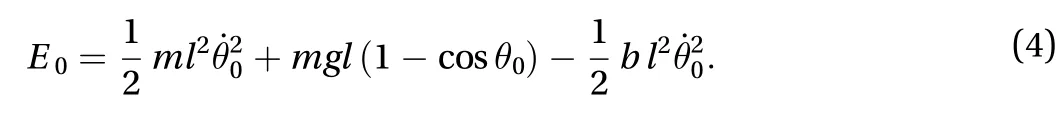
The magnitudeE0can be assumed asthe energy required to rest ore initial conditionsandafter energy extraction,by means of the servomotor and the gear-belt system of Fig. 1.Thus, E0is subtracted from the generation in Eq. (3).

To obtain realistic simulations, the input excitation of Eq. (1)corresponds to time histories of acceleration measured during the passage of a Thalys HST. The measurements were performed during homologation tests of the HST track between Brussels and Paris, and gently provided by Degrande and Schillemans [3], who made the data available to other researchers.

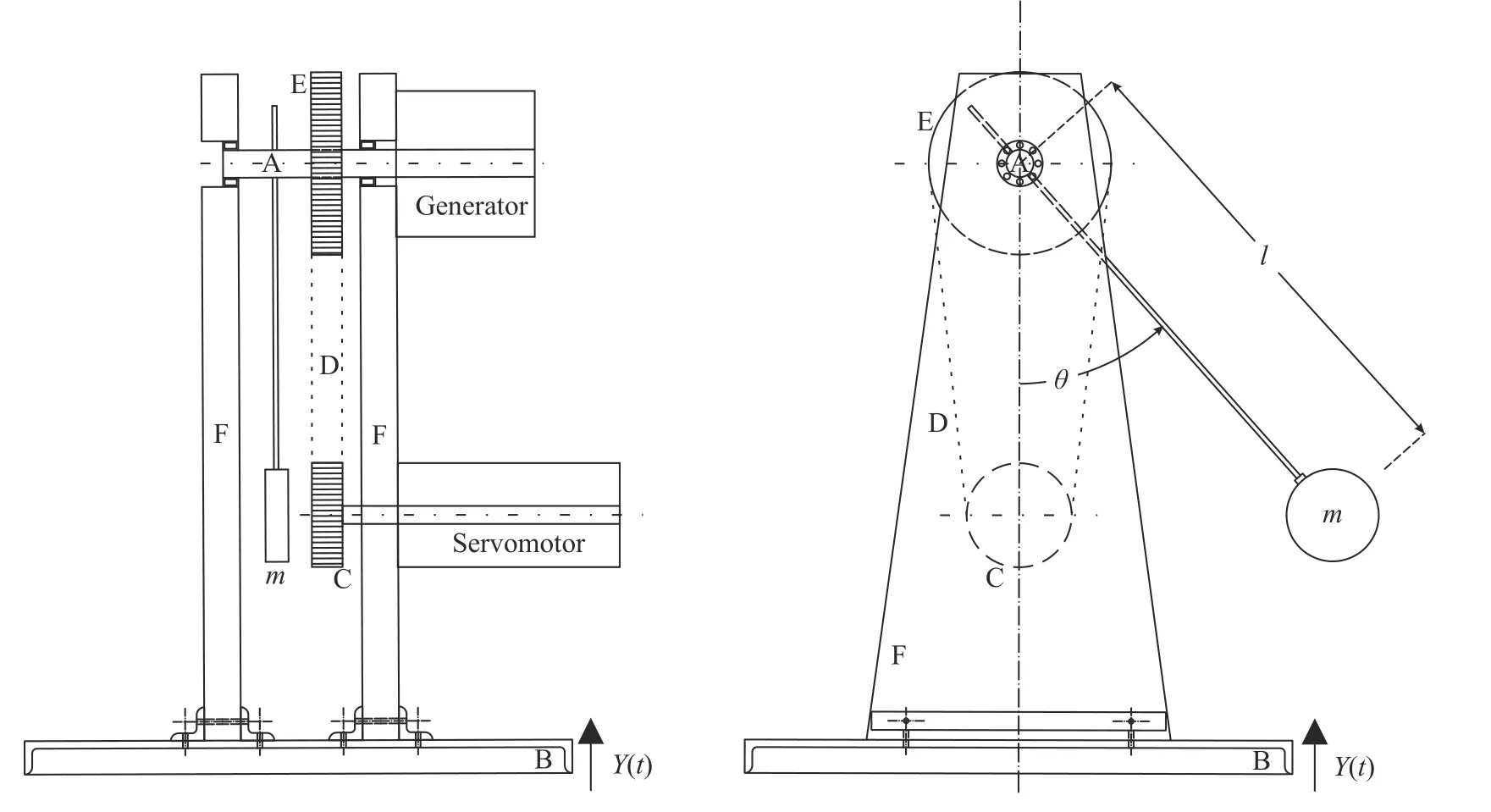
Fig. 1. Schematic diagram of a pendulum harvester (side views). A: pendulum axis, B: pendulum base, attached to the track or sleeper, C-D-E:gear-belt coupling between the pendulum axis and the servomotor, which provides the initial conditions to the pendulum, F: frame.

Four different data sets are considered in our work, at different train speeds v: t12, t22, and t23, corresponding to measurements on the rail, and t21, measured on the sleeper. These vibrational data is presented in Fig. 2. The denominations follow the nomenclature of Ref. [3].

Since the parametric pendulum a potential well system, a period-1 rotation represents its most energetic state [15] (from now on, we refer to period-1 rotations simply as rotations). Thus,the determination of the physical magnitudes l and m must be related to the ability of sustaining such rotational state. For a parametric pendulum with a sinusoidal excitation given byand m can be estimated by a relatively simple procedure. Setting= 1, Eq. (1) can be written in a dimensionless form as

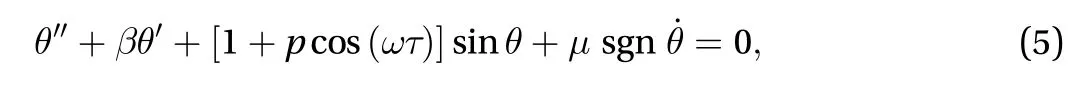
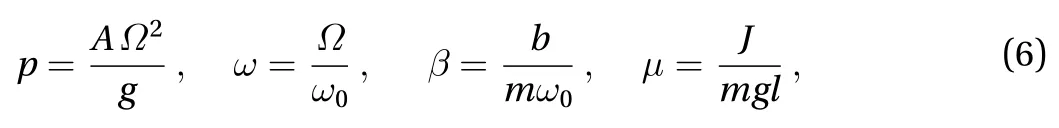
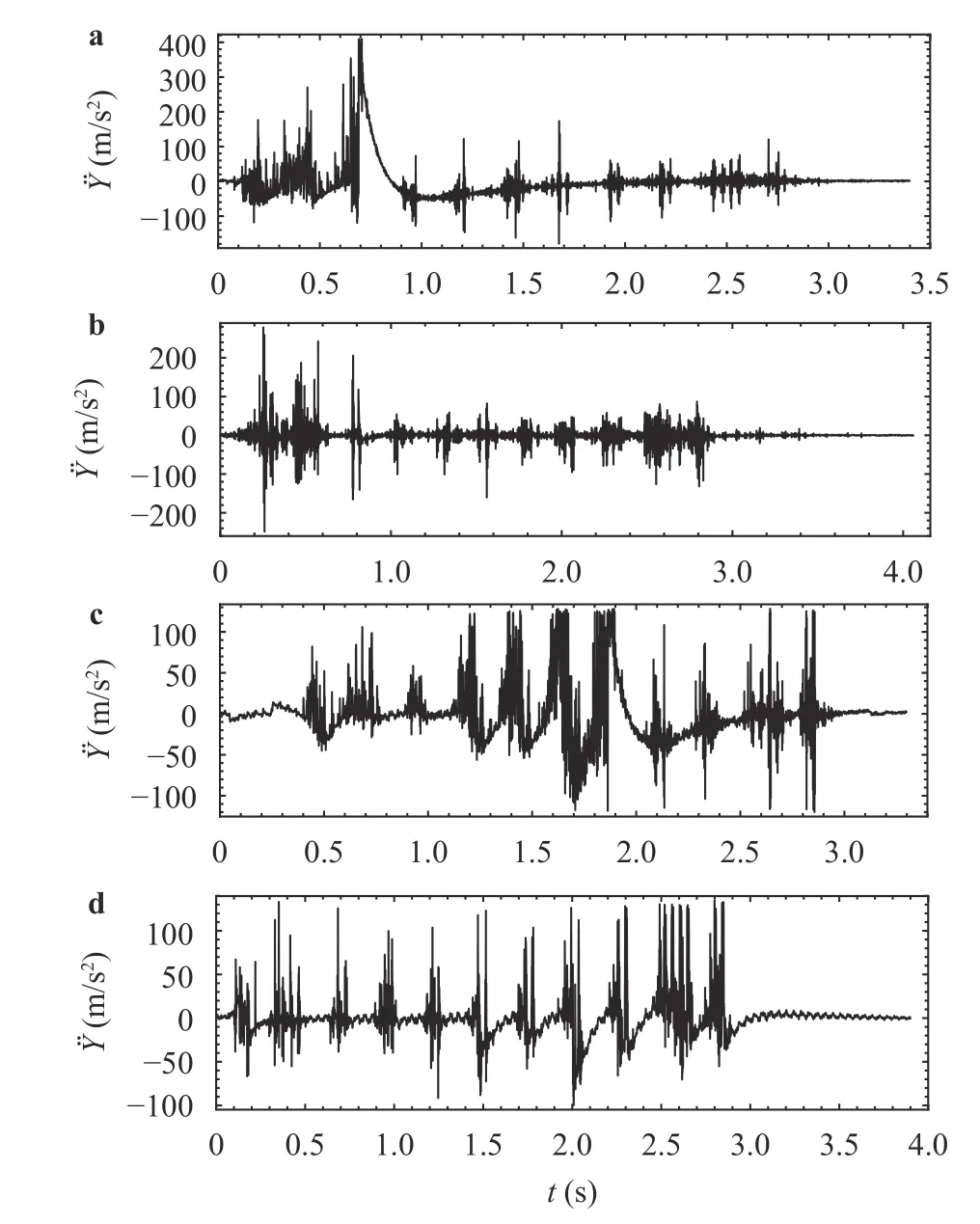
Fig. 2. Time histories of vertical acceleration during the passage of the Thalys HST [3] used in this work. a v = 265 km/h (t12), b v = 271 km/h (t22), c v = 289 km/h (t23), d v = 256 km/h (t21).

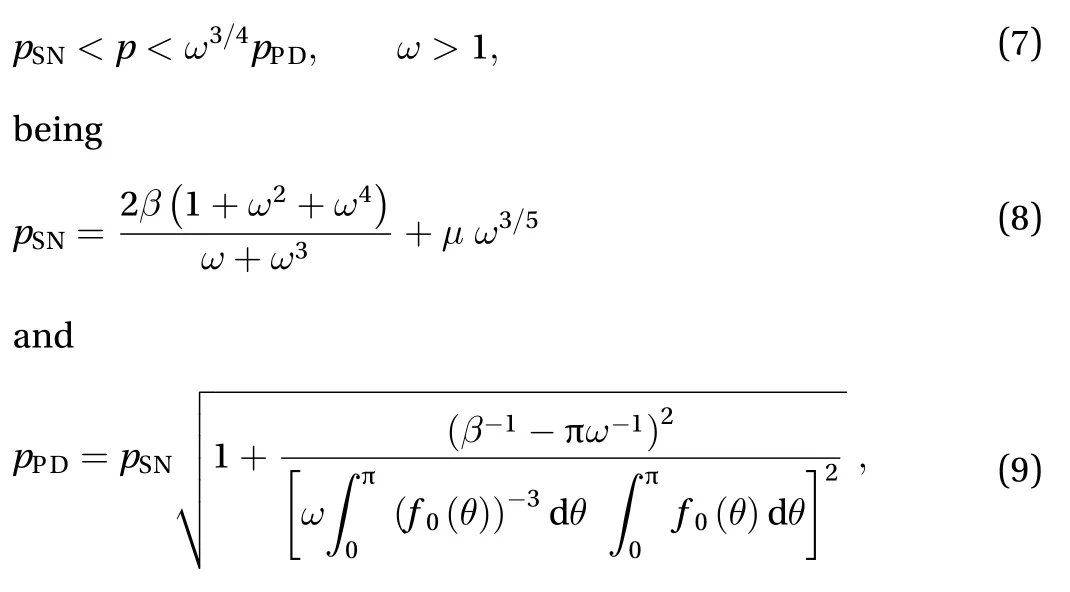
where f0is the solution for the unperturbed pendulum. The fulfilling of Eq. (7) implies that the pairlies inside a particular area in the parameter spacecalled “rotation zone” [17]. This is shown in Fig. 3. Now, given the definition ofin Eq. (6), we can define

For a sinusoidal excitation, the fulfillment of Eq. (7) ensures the existence of rotations. For stochastic excitations (as the vibration of a passing train), an analogy can be drawn to provide a clue to obtain such motion. It is not possible to define values for A andin the case of a stochastic motion. Hence, rotations cannot be ensured for a given combination of parameters. However,a mean amplitude ASand apredominant excitation frequencystill can be obtained from the stochastic signal. For apassing train,is the fundamental bogie passage frequency [16],namelywhere v is the train speed andLbis the distance between bogies. Using ASandsuitable magnitudes of m and l can be determined through Eq. (6)-(9).

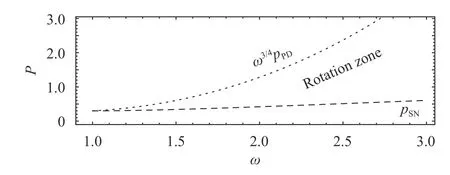
Fig. 3. Rotation zone of the classic parametric pendulum, represented in the parameter space

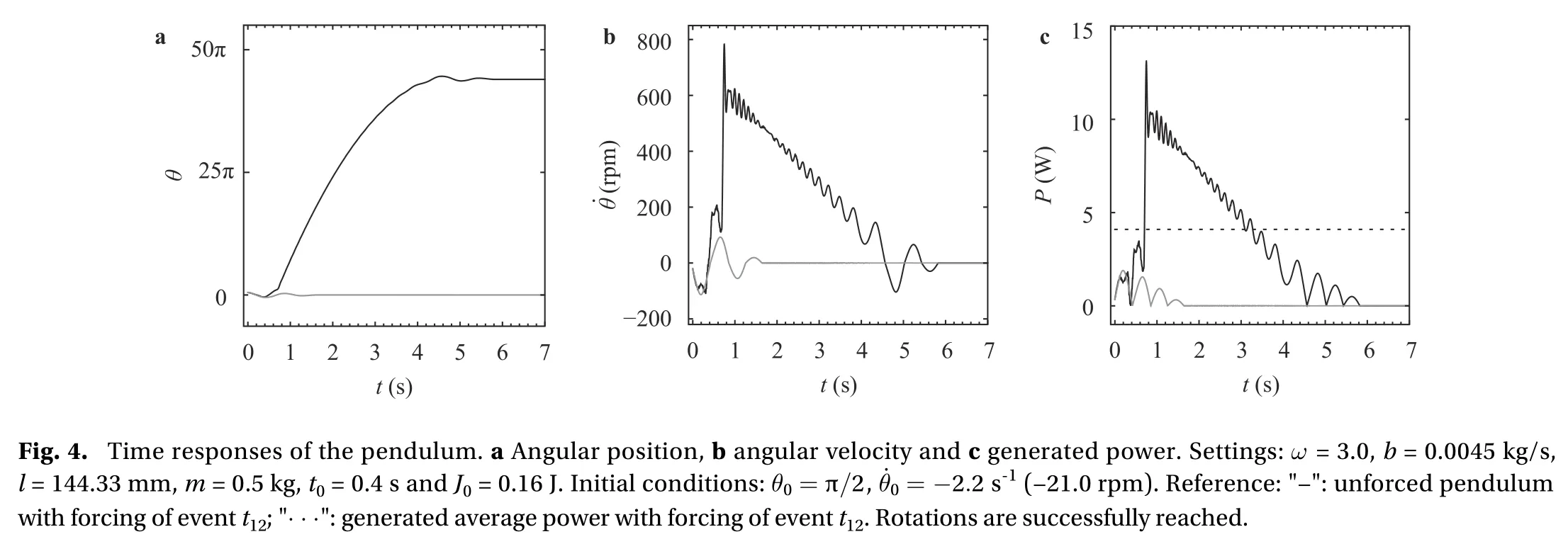
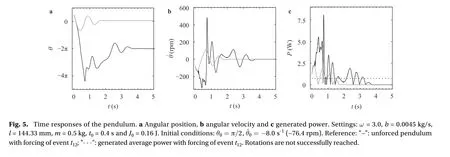
Numerical simulations are performed, in order to evaluate the rotational behavior of the pendulum during the passage of the Thalys HST. We aim to quantify the power that could be generated and to address the influence of initial conditions and viscous damping. Initially, the importance of achieving a sustained rotational motion is studied, to generate a usable amount of power. In Figs. 4 and 5, two different time responses of the pendulum during the forcing event t12are presented. Identical configuration is employed in both cases, except for the initial condition of angular velocity, set as -2.2 s-1and -8.0 s-1, respectively.In Fig. 4, the parametrically forced pendulum reaches and maintains a counterclockwise rotation, completing a total of 20 revolutionsIt stops after ts= 5.43 s, allowing an average power generation of 4.10 W. This is indicated by the horizontal dotted line in Fig. 4(c). In Fig. 5, the motion of the forced pendulum is rotational at first. But right after starting energy extraction(at t0= 0.4 s), the motion becomes oscillatory. At ts≈ 3.75 s, the pendulum stops at its hanging position. Power generation is much lower in this case: 0.73 W. These results are reasonable in view of the definition of average power, Eq. (3), as the integral of angular velocity over time is greater if rotations are achieved.

Gray lines in Figs. 4 and 5, represent the response of the unforced pendulum (i.e., Y = 0 in Eq. (1)), for the same initial conditions. Comparing with the forced pendulum (black lines), the influence of track vibration in the dynamics can be observed.Clearly, much more vibratory energy is transferred to the pendulum if a sustained rotation is reached.

Figures 4 and 5 also evidence that a suitable choice of initial conditionsandis essential to successfully obtain a rotational motion [14]. Thus, a quantification of the amount of power that could be generated for different realistic initial states is required. The influence of initial conditions in nonlinear systems is commonly addressed by constructing the associated basins of attraction, i.e. the sets of initial states leading to a particular attractor. Now, basins are meaningless for a pendulum in the case of time-limited excitations since the responses are entirely transient, being the rest position the only possible attractor.However, a resemblance can be raised: high power generation levels areassociated toinitial conditions leadingto a sustained rotation.Asa general rule, itcan be established that if＞ 3 W is generated, it means that rotations are reached and maintained.

Figure 6 shows contour plots of average power, for every initial states fulfillingand[15].Figure 6(a) corresponds to setting= 2.5, for a pendulum under the excitation of event t12. The well-known fractal dynamics of the parametric pendulum is observed [13, 14]. This fractalization is due to the dynamics of the parametric pendulum but also to the stochasticity of the excitation [20]. For trajectories starting inside the two symmetrical basins in the neighborhood ofnumerical simulations indicate a maximum average power of 5.9 W. However, initial conditions must be very precise to obtain such power, being 3-5 W a more realistic prediction.

As could be expected, the fractal topology evolves asis varied. In Fig. 6(b),is increased up to 3. The basins observed in the previous example are identifiable and keep their size, but move to zones of higher initial velocity. Realistic power levels of 3-6 W could be obtained, which are higher than those of example in Fig. 6(a). This is logical since rotations become faster asincreases [17]. Maximum levels of 7.7 W are observed in this case in the neighborhood of= ±5 s-1, with

Similarly, Fig. 6(c) shows that less power could be generated ifis decreased to 2. This is because rotations are slower. Besides, reducingimply reducing l (note that l = 64.14 mm in this example). Thus, the pendulum may result to be very short (in practical terms) to have a massive bob, as we consider in the previous two examples. A reduction of both mass and length implies an increase ofand. Such increase moves upwards the curve pSNof Fig. 3, thus placing our system closer to the lower border of the rotation zone [17, 21]. Due to this situation, smaller basins are obtained, and rotations become even more difficult to achieve.

From the three examples above, it follows thatmust be as high as possible. Now, the lower boundary of the rotation zone(Fig. 3) growsexponentially from= 3on (provides a good approximation of such boundary up to= 3). In practical terms,rotations ofthe pendulum areimpossible to obtain for＞ 4.5.Thus, a reasonable choice seems to be= 3, which is considered in the next examples.

An average power of 3-4 W is expected in the case of event t23, as shown in Fig. 6(d). Topology is very different if compared to Fig. 6(b), confirming that dynamics can be strongly influenced by the vibratory pattern of the track. This represents a drawback, preventing a priori determination of a suitable set of initial conditions which work for all cases. Nevertheless, in view of the high power generation predicted by the simulations, the implementation of a control action of low power consumption could be a viable option [22, 23]. The servomotor schematized in Fig. 1 could be an option to implement such control [23].

Figure 6(e) considers the vibration of a sleeper as input motion (eventt21). Simulations indicate that rotations are very diffi-cult to reach,as＞ 3 W is obtained only for areduced set ofinitial conditions. Given the low power generation, a control action is not a choice. Thus, energy extraction seems to be not viable in this case. An even worse situation is presented in Fig. 6(f) (event t22), as rotations cannot be obtained. In both examples, the passage of the train produces a low vibration. The average amplitude ASis small and so is p, from Eq. (6). The system is placed almost over the curve pSNin Fig. 3 and thus obtaining rotations is a very difficult task.

Damping must be as low as possible in order to maximize power generation [15]. For all the examples presented, b =0.01 kg/s was assumed as a realistic magnitude [8]. But given the influence of damping in the dynamics of the parametric pendulum [18], a situation of increased damping must be considered.In a real life application, such increase can be generated by a problem with the bearings, a progressive misalignment of the pendulum axis, a sudden modification in the orientation of the bob or, in general terms, any malfunction caused by the long term operation condition of the system. In fact, due to malfunctions, damping can become of a very complex nature. We do not intend to analyze in depth the topological changes in the dynamics produced by damping, but only its influence as a mere dissipative energy mechanism.Thus, wesimplify the treatment by only increasing thedampingcoefficient b (or).A progressive increase in damping is considered in Fig. 7. In Fig. 7(a),has been raised 10 times with respect to Fig. 6(b) (= 0.0024). Power generation is lower since rotation basins are small, but still 3-5 W could still be obtained relatively easy. Such tendency continues in Fig. 7(b): 3-4 W of average power are still possible to obtain, but basins are very small. Rotations are very difficult to obtain in the example of Fig. 7(c). Again, the system is placed very close to the curve pSN, and energy extraction could not be possible. However, damping has been raised 40 times with respect to the case of Fig. 6(b), and rotations are still reached.

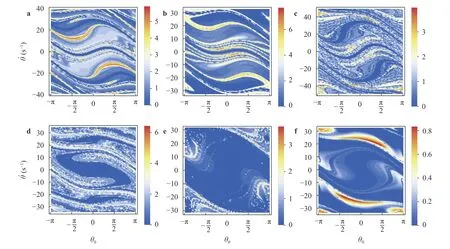
Fig. 6. Output average power levels (in W) as function of initial conditions, corresponding to forcing events of Fig. 2. a Event t12, = 2.5 (l =100.23 mm). b Event t12, = 3.0 (l = 144.32 mm). c Event t12, = 2.0 (l = 64.14 mm). d Event t23, = 3.0 (l = 121.35 mm). e Event t21, = 3.0 (l =154.65 mm). f Event t22, = 3.0 (l = 138.01 mm). In all cases: m = 0.5 kg, J0 = 0.25 J, b = 0.01 kg/s and t0 = 0.4 s.

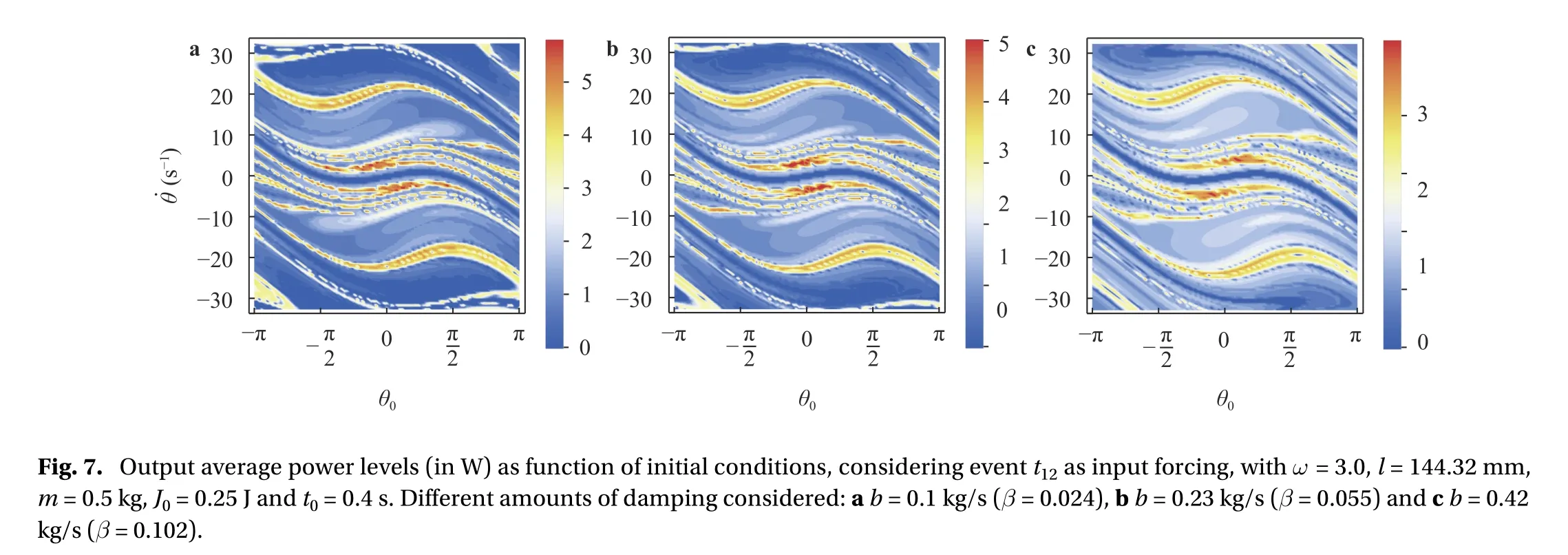
Finally, some comments on the influence of torque J and triggering time t0. With a very low damping, the amount of energy that could be extracted from the pendulum motion is almost independent of the torque J. But value of J depends on power requirements. For example, if warning lights at grade crossings must be fed, the energy must be extracted in a few seconds, and thus J must be as high as possible. Since J is proposed to be constant in Eq. (1), energy extraction must start after a time t0＞ 0 in order to allow the pendulum to increase its kinetic energy and produce rotations. Energy extraction as proposed in Eq. (1) is a possibility, which is equivalent to consider a bi-linear dry friction. However, different strategies could be considered in order to avoid the delay t0and optimize generation.For example, the torque J could be applied gradually, or assumed as proportional to the angular velocity of the pendulum.From a trial and error tactic, we assumed t0= 0.4 s and J = 0.25 J in all the examples. This allows in most cases developing rotations (as long as they are feasible) and stopping the pendulum completely after a time tS, which is approximately equal to the duration of the input acceleration signal.

The possibility of recovering energy from the passage of HST was addressed. Due to the simplicity of its mechanisms, a device based on the parametric pendulum was considered as harvester.After several simulations, we concluded that if viscous damping is sufficiently low (0.01 kg/s), a single pendulum with length 120 mm and mass 0.5 kg could be able to generate average power levels on the order of 5-6 W. This represents an encouraging prediction, since 10 W is the required power to illuminate one high efficiency light-emitting diode (LED) lamp [1].

A sustained rotational motion of the pendulum is strictly required to generate a usable amount of power. This should not represent a problem since rotations are a common response of the parametric pendulum. However, their associated basins (i.e.the sets of initial conditions producing rotations) depend of the input forcing. Now, given the high level of average power predicted by the simulations, the implementation of a control action of low power consumption could be a choice [22, 23] to overcome such drawback.

The behavior of the potential harvester against an increase in damping was addressed. Simulations showed that rotations are robust, as 3-5 W could still be obtained after rising damping 10 times. Nevertheless, energy must be saved due to a latent need for an active control system, which should be fed from the harvester itself. Consequently, keeping a low viscous damping represents a crucial topic.

Acknowledgements

The authors would like to thank the support of Secretary of Science and Technology of UTN, CONICET, the National Agency for Scientific and Technological Promotion and Engineering Department of UNS. Professor Franco Dotti dedicates this article to the beloved memory of his childhood friend Lucía Trotz (1975-2018).