让初中数学“相似三角形”教学更有效

☉浙江省桐庐县实验初级中学 周建洪

在初中数学平面几何中，相似三角形是继全等三角形后第二个重要的知识点.与全等三角形相比，相似三角形的内容更丰富也更复杂，难度上也有所提高.为了让教学更有效，在相似三角形的教学中，从核心素养观角度，教师应从哪几个方面入手呢？本文结合课堂教学实践谈几点看法，供参考.

一、教师要创设情境，搭建学生主动学习的桥梁

创设情境，引导学生积极思考，经历“操作—观察—探索—说理”的数学活动过程，发展合情推理和有条理的表达能力，是相似三角形的教学目标，如何实现这个目标呢？教师可以从以下几个方面入手；

1.从复习旧知入手，引导学生探究新知

在相似三角形的第一节课上，教师可以让学生通过作图，达到由旧知引新知的目的.

（1）作图活动.

活动1：如图1，画三条互相平行的直线l1、l2、l3，再任意画两条直线a、b，使a、b分别与l1、l2、l3相交于点A、B、C和点D、E、F.

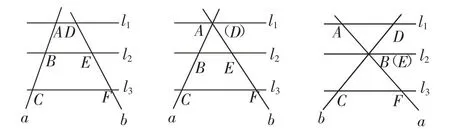
图1

（2）探索新知.

提出问题：

①度量所画图中AB、BC、DE、EF的长度，并计算对应线段的比值，你有什么发现？

②如果任意平移l3，再度量AB、BC、DE、EF的长度，这些比值还相等吗？

活动2：如图2，在△ABC中，点D、E分别在AB、AC上，且DE∥BC，△ADE与△ABC有什么关系？

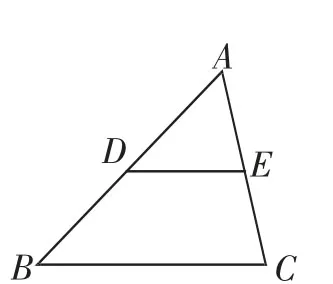
图2

（3）得出结论.

两条直线被一组平行线所截，所得的对应线段成比例.

平行于三角形一边的直线和其他两边相交，所截得的三角形与原三角形相似.

2.从实际问题入手，引导学生探究新知

学习的目的是解决实际问题，反过来实际问题的解决催生了数学知识的形成，在学习相似三角形判定定理2时，我们可以借助实际问题达到形成新知的目的.

（1）引发认知冲突.

为测量隔湖两点A、B的距离，先在湖外确定一点O，使点O能直接到达A、B两点，分别在AO、BO的延长线上取点C和D，使，，如果测得CD=a，那么AB=2a，这是为什么？

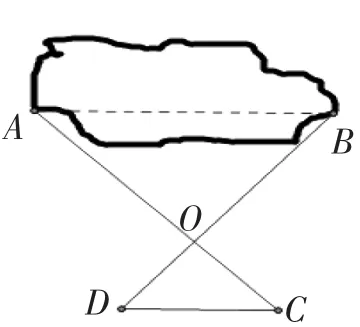
图3

（2）数学活动.

教师要求学生自学课本知识后完成下列问题：

①同桌两人分别画△ABC和△A1B1C1，使AB=2，AC=3；A1B1=4，A1C1=6，然后比较，看是否相似.

②同桌两人分别再画△ABC和△A1B1C1，使AB=2，AC=3；A1B1=4，A1C1=6，且∠A=∠A1=60°，然后比较，看是否相似.

（3）形成新知.

两边及其夹角分别相等的两个三角形全等.如果把其中两边相等的条件改为：“两个三角形的两边成比例”，保留“夹角相等”的条件，这两个三角形相似吗？

已知：如图4，在△ABC和△A′B′C′中，∠A=∠A′，A′B′∶AB=A′C′∶AC.求证：△ABC△A′B′C′.

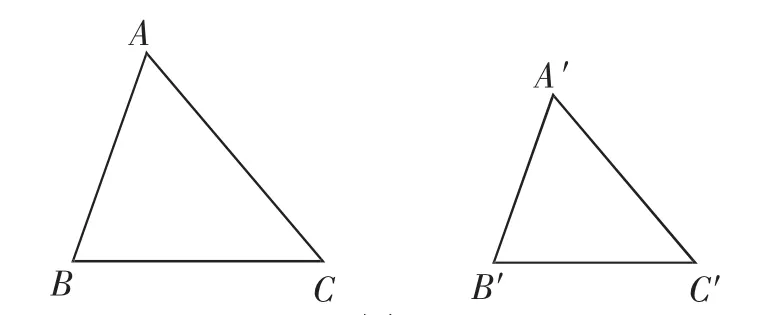
图4

证明：在△ABC的边AB、AC（或它们的延长线）上分别截取AD=A′B′，AE=A′C′，连接DE.又∠A=∠A′，则△ADE△A′B′C′.

由A′B′∶AB=A′C′∶AC，得AD∶AB=AE∶AC.

于是得到判定定理2：“两边对应成比例且夹角相等，两三角形相似.”

二、教师要积极探索，打开学生感受数学价值的通道

数学教学不仅要求教师传授数学知识，更要求教师在进行探索的活动过程中发展学生的探索、发现、归纳意识和合作交流的习惯，发展学生的合情推理能力和初步的逻辑推理意识，体会数学思维的价值.

1.在拓展性问题的解决中，培养学生的能力

设计拓展延伸的目的是进一步加深学生对相似判定方法的理解，同时培养学生分析问题、解决问题的能力.比如，可以设计如下问题：

问题1：要制作两个三角形框架（形状相同），其中一个三角形框架的三边长分别为4、6、8，另一个三角形框架的一边长为2，它的另外两条边长应当是多少？你有几种答案？

问题2：如图5，正五边形ABCDE的5条边相等，5个内角也相等.

（1）找找看，图中是否有黄金三角形？

（2）点F分别是哪些线段的黄金分割点？

问题3：过△ABC（∠C＞∠B）的边AB上任意一点D作一条直线与另一边AC相交，截得的小三角形与△ABC相似，这样的直线有几条？请把其一一作出来.

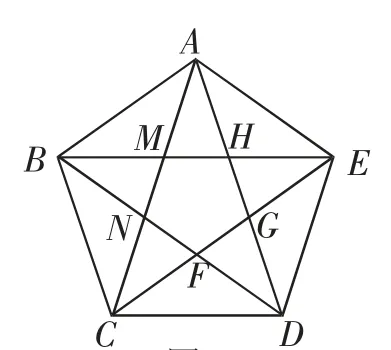
图5

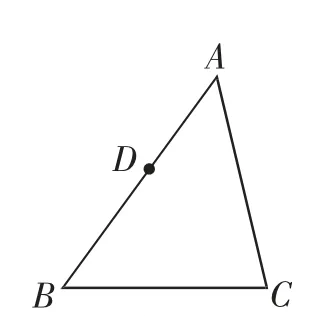
图6

2.在实际问题的解决中，感受数学的实用价值

数学一直被认为是抽象的理论，其实数学就在我们身边，用所学知识解决身边的实际问题可以激发学生的学习热情，更能让他们感受数学的实用价值与文化价值.

例如，利用黄金分割比解决实际问题.

问题4：在人体躯干（肚脐到脚底的距离）与身高的比例上，肚脐是理想的黄金分割点，即此比值越趋于0.618，就越会给别人呈现一种美的感觉.倘若一位女士的身高为1.60m，躯干与身高的比为0.60，为了追求完美，她想搭配一高跟鞋以达到这一效果，她应选择高度约为（ ）的高跟鞋

A.2.5cm

B.5.1cm

C.7.5cm

D.8.2cm

再如，利用相似三角形的性质求线段长.

问题5：东方国际学校门口的栏杆如图7所示，栏杆于水平位置BD围绕点O旋至AC位置，已知AB⊥BD，CD⊥BD，垂足分别为点B、D，AO=4m，AB=1.6m，CO=1m，则栏杆C端应下降的垂直距离CD为（ ）.

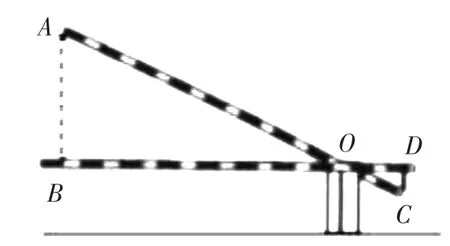
图7

A.0.2m

B.0.3m

C.0.4m

D.0.5m

感受数学，就是感受数学中的思想方法，感受数学对发展智力的作用，感受数学在日常生活中的应用价值，帮助学生树立正确的数学观，对提高教学效率有着不可小觑的作用.

三、教师要积极引导，帮助学生完善知识结构

在以往的教学中，我们经常发现当“相似三角形”的教学完成之后，问学生这一章我们学了哪些知识，学生的回答或不全面，或回答不上，也许是这一章内容太丰富的缘故.因此，教师有必要帮助学生对这一章的知识点进行归纳与整理，尤其是如何判断三角形相似和相似三角形的性质是教学的重点，要让学生在理解的基础上强化记忆，因为这是相似三角形解题的“基本工具”.

如何构建“相似三角形”的知识结构呢？应该渗透到日常教学的每一节课中，在每节课结束时，都要加以总结与提升，教师可以引导学生来完成.比如，教师可以问学生：“通过这节课的学习，你学习到什么新知识？获得了什么经验？还有什么疑问？”以此来培养学生反思自己学习过程的意识，充分发挥学生的主体作用，从而培养归纳、整理、表达的能力.在复习阶段，更要提纲挈领地引导学生加以总结与完善，帮助学生形成思维导图，如图8：

“会当凌绝顶，一览众山小”.整体把握教材，有助于学生把问题看得更清，理解得更透彻，从而快速找到各知识点之间的联系，达到快速解决问题的目的.

教学是一个系统工程，每个细小的环节都不可忽视.除了上面提到的几点，在“相似三角形”的教学中，教师还要注重数学学科核心素养的培养，如逻辑推理和数学运算能力的培养，这是本章教学的重点，教师应该把这种教学观落实到每节课中去，这样才能让“相似三角形”的教学更有效！