经典几何问题及变式教学：复习备考的关注点——从一道几何综合题的讲评说起

☉江苏省常熟市王庄中学 王裕龙

进入中考二轮复习阶段，常常开展综合试卷训练，训练之后就要安排讲评，如何对一些有难度的综合题进行讲评往往需要精心设计.本文从一道几何综合题的讲评出发，进一步阐释我们对解题教学的一些思考.

一、几何综合题的解法与讲评案例

几何综合题：（2019年4月某校中考模考卷，倒数第二大题）如图1，等边三角形ABC中，D为边BC上一点，点D关于直线AB的对称点为点E，连接AD、DE，在AD上取点F，使∠EFD=60°，射线EF与AC交于点G.

（1）设∠BAD=α°，求∠AGE的度数（用含α的式子表示）；

（2）探究CG与DE之间的等量关系，并证明.

思路贯通：（1）把目光聚焦在△AFG中，借助三角形内角和，可分析出∠AGE的度数为（60+α）.

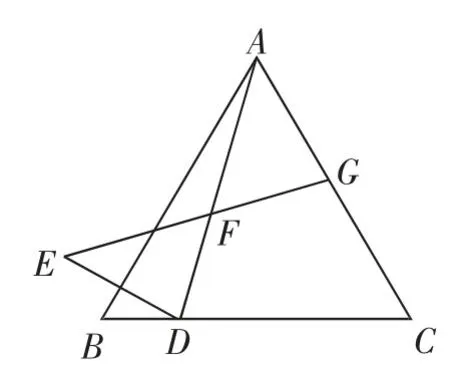
图1

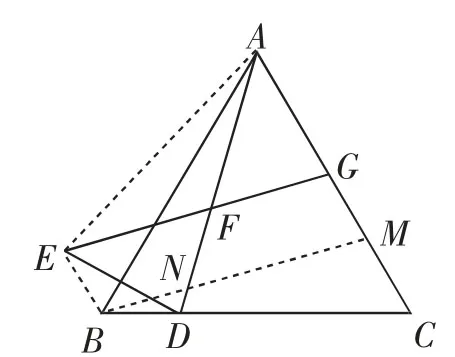
图2

（2）如图2，在AC上截取CM=BD.由全等容易证出BM=AD.再利用（1）中的进展，导角（∠EAG=∠EGA=（60+α）°）证出AE=GE，从而有AE=AD=BM，于是EG=BM.进一步导角（∠EFD=∠ENM=60°）证出EG∥BM.于是四边形BEGM是平行四边形，所以GM=BE=BD=CM.于是M为CG的中点.所以CG=2BD.而DE=，思路接通，即2DE=.

反思回顾：在上述思路中，有几处关键步骤，分别是：证出AE=GE；作出辅助线BM，证出四边形BEGM是平行四边形；证出M是CG的中点；想清△BDE是含120°的等腰三角形.

不同思路：如图3，延长GE、CB交于点P，通过导角证出∠PBE=∠ABE=∠C=60°，可得BE ∥CG，∠PEB=∠PGC=∠ADB=∠AEB=120°-α°.于是可证△ABE△PBE，从而得BP=BA=BC，PE=AE=EG，于是BE是△PCG的中位线，从而贯通思路.

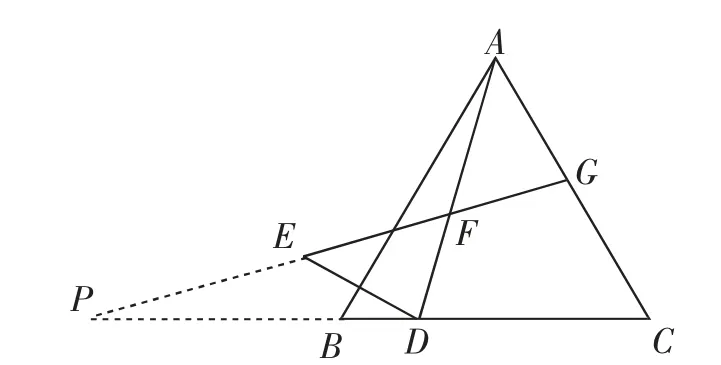
图3

解题教学微设计：“从等边三角形出发”.

引例热身：如图4，等边三角形ABC中，点D、M分别在边BC、AC上，且BD=CM，连接AD、BM，它们的交点为G.

（1）求证AD=BM；

（2）证明（1）之后，请再提出两个问题并解答.

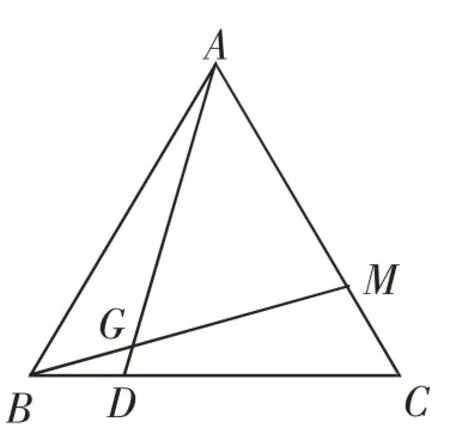
图4

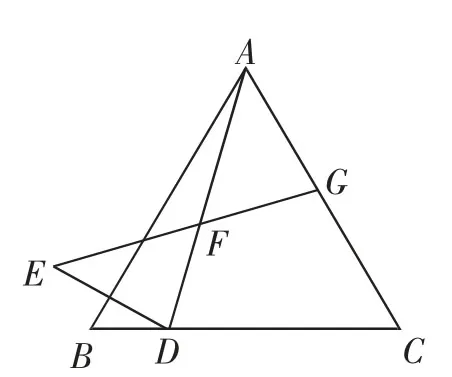
图5

教学组织：学生在证出全等之后，可以继续提出一些角相等的问题，认识深刻的也可得到AD、BM的夹角的度数.

考题讲评：见上文几何综合题.

教学组织：安排学生逐个分析上面考题“反思回顾”中提到的几处关键步骤，在少数优秀学生贯通思路之后，让其他学生再复述思路.为了巩固这道考题的讲评效果，再给出一道变式改编习题.

变式再练：如图5，等边三角形ABC中，D为边BC上一点，点D关于直线AB的对称点为点E，连接AD、DE，在AD上取点F，使∠EFD=60°，射线EF与AC交于点G.

（1）求证GE=AD.

（2）小睿提出一个等式：CG=k·DE，并发现实数k是一个定值.请判断“小睿的发现”是否正确，并说明理由.

变式意图：第（1）问在原考题第（1）问的基础上就可得出，为第（2）问提供了铺垫.第（2）问在原考题第（2）问的基础上变换不同的设问方式，本质上是一样的，讲评时要引导学生体会“它们是一样的”.

二、几何综合题解题教学的几点思考

1.精心预设几何综合题的教学组织

几何综合题作为一份试卷中的把关题之一，往往能顺利完整解答的学生并不是很多，在讲评之前，教师要做好充分的课前准备，主要是针对几何综合题的深刻理解，特别是几何题几个小问之间缺少的铺垫步骤，在备课时需要充分想清，然后对如何引导学生突破关键步骤进行铺垫式设问，这也是上面讲评过程中我们预设一个“引例热身”的教学立意.此外，在讲评较难问题之后，还可基于原考题的“结构”进行必要的变式改编，以便学生进行巩固训练.

2.解题教学进程让学生讲关键步骤

在讲评较难的几何综合题时，需要教师主导的启发式讲授，但是当关键步骤得到突破之后，教师就需要充分“让学”，让学生学，让学生讲.比如，上文综合题讲评时，当关键步骤都接通之后，就安排学生进行整个思路过程的讲述，然后安排两到三人进行复述，在复述的过程中可以看出学生对该题解题思路是否真正理解，同时可以让一些“后进生”赢得时间充分理解、想通思路和解法.想来，我们常常在观摩一些专家教师的课堂教学中听到“请你再说一遍”，大抵也是这个意图吧.

3.解后揭示几何综合题的深层结构

解题教学在学生都能顺利贯通思路之后，还需要跟进一个重要的教学环节，即引导学生解后回顾反思，促进学生对几何综合题的深层结构有较为深刻的理解，对解题过程中的关键步骤更加明确，还可帮助学生提炼一些基本图形及性质，特别是教材上提到的一些经典问题、高频习题都可进行必要的链接、对比，让学生感受一题多变、多题归一，坚持这样做，有利于学生“做一题，会一类，通一片”.

三、复习备考要特别重视经典几何问题的变式教学

1.重视选用教材中的经典几何问题

当前复习备考有一个很大的选题误区，即每节课都大量选用所谓的中考真题，而且这些中考试题来自全国各地中考试卷，似乎链接了中考真题就是在有效、精准备考，殊不知，全国各地中考试卷风格差异巨大，各具特色，多数中考试题并不适合本地的复习备考.如果实在要在复习中体现中考元素，也应该尽可能多关注本地区中考真题的考查特点，而不要盲目选取外地的中考试题，特别是一些来历不明的所谓名校考题、模考试题、“网红题”.相对而言，比较重要的一个选题方向是到教材上挑选经典几何问题进行复习，因为教材上所选的例、习题都是经过精心挑选的，几何图形简洁、性质深刻，值得思考，中考命题都是“依标靠本”，而经典几何问题常常是中考命题组改编的重要来源，所以师生在复习备考时要充分重视教材中的经典问题，而不能左顾右盼，舍本逐末.

2..经典几何问题教学时要注重变式

经典几何问题在复习课上选用时，并不是简单的让学生再做一遍、多做几遍，而要尽可能发挥经典几何问题的教学功能，本文选用的一道几何综合题其实就是对经典几何问题的变式改编，只是在两个不同设问中拉开了“很大的距离”，学生解题时需要接通这些“距离”，接通的过程就是把很多经典问题通过辅助线完善起来、连接起来的过程.这就启发我们，在复习备考过程中，要善于把经典几何问题进行改编包装，以训练学生识别这些包装，练就“火眼金睛”，达到快速解题的目的.关于变式改编，需要教师修炼命题能力，比如，针对经典几何问题，可以对问题进行必要的拓展，深入挖掘可能的结论；也可针对经典几何问题的条件和结论进行置换，研究互逆命题，并证明它们是否仍然是真命题；还可以将经典几何问题以新定义的方式包装改编，让学生识别问题结构.可以发现，数学教师的专业基本功除了“善于举例、善于提问、善于优化”（郑毓信教授语），还需要钻研命题功夫，不只是出一份试卷时才需要命题能力，日常课堂教学中针对例、习题的改编和变式更需要我们有扎实的命题功夫.