在解决问题中发展学生的数学学科核心素养——以“勾股定理的简单应用”为例

☉江苏省张家港市港区初级中学 黄嘉玲

近来笔者做了一节全校数学教师的示范课，该节课所授内容是“勾股定理的简单应用”.从课程标准的角度来看，本节课是为了在解决问题中发展学生的数学学科核心素养，培养学生的数形结合思想方法.在常规教学中，多是辅助以大量的练习题，在题海战术中深化学生的数学思想.通过多年的教育实践发现，初中生没有成人的毅力，大量的练习会让他们望而生畏.如何才能在课堂上跳出题海，又能发展学生的数学学科核心素养呢？笔者将本节内容所采取的一些做法留于纸上，旨在与各位一线教师进行更加深入的交流.

一、抓住授课内容的数学学科核心素养，确定教学的目标

通过前面几节内容的学习，学生已经明确了勾股定理将几何图形进行了数字化处理，突出了“数形结合”和“转化”的数学思想，融入了数学学科核心素养.而本节是运用勾股定理及直角三角形的判定条件去解决实际问题，这不但能够发展学生分析问题的能力和表达能力，同时培养了学生的逻辑推理能力及合作交流的意识.

通过以上分析，笔者确定了教学的目标，由此考虑到在传授知识时概括出勾股定理、直角三角形的判定定理（即勾股定理的逆定理）在应用方面的区别，在实际应用中提出二者的区分和应用能力，也为本节知识的课时计划的编写奠定了基础.

二、诱发授课内容的数学学科核心素养，创设教学的情境

作为一线教师，不但要了解学生的学情，而且要适应现代中学生的心理特征.他们有强烈的好奇心，有刨根问底不放弃的毅力，所以，创设与所授知识相关的情境是课堂教学的重要环节，是激发学生求知欲的引擎.笔者是这样创设情境的：

《九章算术》中有一道“折竹”问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”然后用电子白板展示该背景材料，其展示配旁白解释（见图1）.

创设这样的质疑情境，一方面，让学生理解中国古文化的博大精深；另一方面，能激发学生的探究兴趣.让学生在情境中感受勾股定理应用的意义，体会数学思想，形成学科核心素养.

在学生鼓舞了斗志，有了探究知识的欲望之际，可以回顾已有的勾股定理的知识，为后面勾股定理的简单应用打下基础.预设这样的问题：

问题1：直角三角形的角有什么关系？边有什么关系？

问题2：若一个三角形的三边存在a2+b2=c2这样的关系，则其对应的角有什么关系？三角形是什么三角形？

创设的两个勾股定理的相关问题是建立在学生的激情之上的，学生通过情境的诱发能够快速进入探究知识的角色，为课堂后面环节的展开埋下了伏笔.

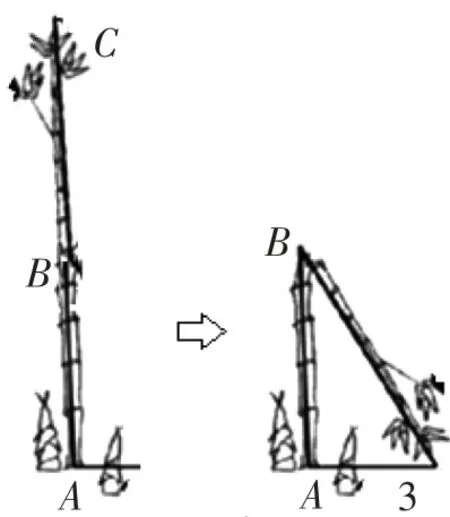
图1

3.提炼应用紧扣数学学科核心素养，在思考中发展能力

让学生进入知识的主体，在课堂练习的思考中培养能力是教学的终极目标.让学生在实际问题中概括出勾股定理、直角三角形的判定定理的区别是教学的重点.在分析问题中去观察、比较；在解决问题中去合作、交流；在释疑问题中去探究、求索.在课堂上，笔者设计了两道助学课堂训练题：

练习1：用电子白板出示：如图2，在风平浪静的湖面上，有朵垂直于水面的荷花，高出湖面3m，某学生用手将花朵拉到齐及水面，荷花移动的水平距离为4m，请问：荷花所处位置的湖深是多少？

练习1是较为简单的勾股定理的应用问题，采取学生自主练习来完成.在课堂上，让两位中等程度的学生在黑板上板演，其余学生在完成任务之后在小组内进行交流，然后看黑板，由考虑成熟的学生进行点评，规范步骤、统一解法.

图2

为了让学生通过练习1进一步了解勾股定理的应用范围，给出下面的课堂练习，让学生在非直角三角形中学会寻找勾股定理的应用.

练习2：用电子白板出示：如图3，在△ABC中，AD=12，AB=13，BC=7.5，D分BC为2∶1.求AC的长度.

设计练习2的目的在于让学生能够举一反三，逆向思维.练习的解决途径是多元化的，应用勾股定理来判断直角三角形，采取学生独立思考的方式进行.解题途径可以百花齐放、百家争鸣，但最终必须让学生回归课本，理解勾股定理的应用的真正意义.

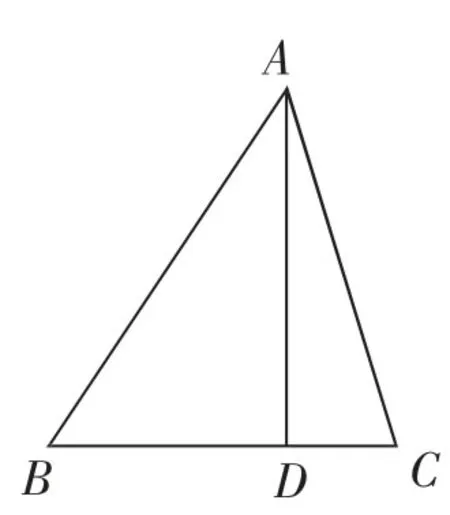
图3

四、熟练掌握应用数学学科核心素养，在释疑中提升素养

课堂的精华在于对知识的理解与应用，需要一种对课堂气氛的烘托.换句话说，要让学生在激情饱满和自然和谐的氛围中深化所学知识.因此，这个环节的设计旨在让学生利用勾股定理解决问题，将几何概念和将未知问题转化为已知问题来解决的化归思想植于学生的脑海，形成学生的学科素养.

变式提升1：用电子白板出示：图4是某橱窗上拼接的一块有色玻璃，其中，AB⊥BC，AB=6cm，BC=8cm，AD=24cm，CD=26cm.计算这块有色玻璃的面积.

这个变式提升是学生在对勾股定理所含的核心素养进行提炼之后的一种拓展，通过学生自主独立思考，达成熟练掌握所学知识的目的.在变式提升的解读过程中，要使学生有所感悟，对数学学科核心素养进行建模：一是在求解不规则图形的面积时，需要将“不规则图形规则化”，也就是对不规则图形进行重新切割，尤其是切割为最小化的“三角形”；二是注意特殊性在求面积中的应用.

变式提升2：用电子白板出示：一个长3m的梯子，其顶端靠在墙上，其下端距墙根1.8m，若将梯子远离墙根移动0.6m，则梯子顶端下滑多少米？

本变式练习没有配上相应的图形，旨在让学生自己能够解读文字，将文字转化为相应的图形，这样，通过本变式训练，不但可以培养学生的动手作图能力，也可以达到加深学生对勾股定理和转化思想的理解与运用能力.

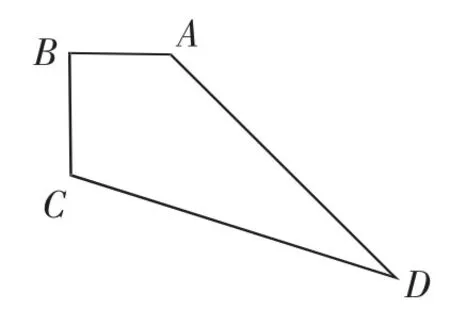
图4

在本节课结束之际，将学生所做的变式练习2的优秀步骤展示在电子白板上，让学生共享成果，有所感悟：

题干转化：在图5中，已知∠ACD=90°，AB=ED=3m，CB=1.8m，BD=0.6m，求AE的长.

图5

在以上两个变式提升中，充分运用勾股定理和直角三角形判定定理（即勾股定理的逆定理）来解决实际问题.变式提升1是求不规则图形的面积问题，需要应用化归思想，将不规则图形的问题转换成规则图形的问题来解决，所以说，解决这类习题时作辅助线尤为重要.在变式提升2中，解决此类问题的关键是画出正确的图形，通过数形结合，确认直角三角形.

总之，笔者的这节示范课在教学设计时，依据了新课标的基本要求，从学生认知的基本学情来选择身边的素材，创设的教学情境充满趣味性和吸引力，让学生在和谐、愉悦的探究氛围中理解了用勾股定理解决实际问题，体现了数学与生活的紧密联系.在课堂教学中，采用了小组合作交流的形式，让课堂更加开放，学生积极参与，热情高.通过课堂媒体的辅助引导，给学生提供更为宽裕的时空和交流的机会，从而达到合作交流的目的，使不同的方法、智慧在交流合作的过程中得到融合.并通过题型变化训练的手段帮助学生构建数学中化归思想的核心素养.