模态转换时间对模态转换过程的影响

唐 琳，孙 波

(南京理工大学 航空宇航系， 南京 210094)

吸气式高超声速飞行器越来越受到各航天大国的关注，吸气式高超声速技术是发展高超声速推进技术的关键技术，它的飞行马赫数十分宽广，从亚声速、跨声速、超声速一直到高超声速，但目前任何一种单一的吸气式发动机(涡轮发动机或冲压发动机)均不能满足要求，因此国内外对组合动力开展了广泛的研究。涡轮机组合循环发动机将涡轮发动机和冲压发动机结合在一起，结合了各自飞行范围的优势，使其具有可水平起降、重复使用、可靠性高、低速性能好等优点，是高速飞行器重要的推进系统选择方案之一[1-3]。

TBCC进气道是TBCC发动机的重要组成部件,它的主要任务是高效率地向涡轮发动机的压气机或冲压发动机的燃烧室提供一定压力、温度、速度和流量的空气,以满足飞行器高超声速飞行的需要，其中包括模态转换过程中同时向涡轮通道和冲压通道提供所需气流，因此能否完成模态转换过程的平稳过渡是决定TBCC发动机是否研制成功的关键。因此，对TBCC进气道模态转换的研究在TBCC设计技术中十分重要[4]。

国内对进气道模态转换过程的研究正在逐渐增多，如曹石彬等[5]利用定常与非定常相结合的办法，分析了模态转换过程中外并联型TBCC进气道的流场变化，性能参数的变化以及模态转换时间的影响。袁化成等[6]对一种外并联涡轮机组合循环发动机进气道进行了基于定常和非定常的模态转换过程气动特性分析，获取了进气道模态转换过程的流动特性。刘君等[7]对一种内并联式TBCC进气道模态转换过程的稳态和非稳态特性开展了数值仿真研究，重点分析了非稳态转换过程对进气道气动性能的影响。孙波等[8]对三种典型并联方案(后开内并联、前开外并联、混合式内并联)在Ma2.1的模态转换工况下进行了稳态仿真分析。向先宏等[9]通过动态数值模拟和高速风洞实验对外并联进气道模态转换特性进行了初步探索研究。

国外单纯对TBCC进气道模态转换过程气动特性开展的研究工作并不太多，Albertson 等[10]在2006年对双通道涡轮基组合循环进气道进行了风洞实验研究。Sauder等[11]在2008年美国宇航局(NASA)报告中对一种Ma=7的二元外并联式双模态TBCC进气道设计过程进行了详尽说明，初步完成了控制模态转换的分流板的设计工作。Slater等[12]在2010年时采用 CFD技术仿真了TBCC进气道模态转换过程的气动性能，并与风洞试验结果进行了对比分析。

本文利用动网格技术及非定常数值仿真方法对外并联TBCC进气道模态转换过程中冲压通道起动和不起动状态的相互转变过程进行数值仿真研究，以获得TBCC并联进气道模态转换过程进气道冲压通道起动特性。

1 进气道几何模型和数值模拟方法

对二元TBCC外并联进气道模态转换过程(涡轮通道由开到闭以及由闭到开)进行数值仿真，上通道为冲压通道，下通道为涡轮通道，模态转换马赫数为2.1，进气道几何模型如图1所示,冲压通道采用三波系设计，内收缩比为1.06，第一，二，三级压缩面的压缩角分别为4.8°，3.9°以10.8°。本文采用的进气道模型的分流板的转轴位置比较靠后，进气道分流板的转轴位置对进气道的模态转换过程有一定影响，因为分流板转轴位置决定了分流板旋转时影响的流场大小。

根据文献[5，13],在进行非稳态计算时，求解器和湍流模型等的选择与稳态计算一致。本文采用N-S方程求解器，采用有限体积法对雷诺平均数进行离散，黏性通量采用二阶中心差分法进行离散，采用RNGk-ε的湍流模型，近壁面处采用标准壁面函数法进行模拟。分子粘性系数采用Surtherland公式计算，对壁面取绝热无滑移固体边界条件。分流板旋转7.2°，选择模态转换时间为100 ms,则需设置其角速度为1.66 rad/s。因此，进行非稳态计算时，设置时间步长为10-5s,时间步数为10 000步。每个时间步内的迭代次数为200次。本文一共选取了三个模态转换时间50 ms,100 ms以及1 s,时间的选取参照了文献[4]，为了获得模态转换时间对模态转换过程的影响，本文选取了3个差值较大的时间，对时间的选取不固定也可以选择其他时间进行模拟计算。

进行非稳态计算前，计算一个稳态流场作为非稳态流场的初始流场。在进行非稳态计算时，需要使用Fluent的动网格技术，本文采用的动网格算法为弹簧光顺和局部重构法，运动区域为外并联TBCC进气道的分流板，将其设置为刚体运动。采用混合网格对外并联TBCC进气道计算域进行划分，其网格如图2所示。分流板附近区域采用非结构网格进行划分，而其他区域采用结构网格进行划分，这样既可以保证分流板转动时其附近的网格进行动态更新，又没有降低其他区域的网格质量。整个进气道的网格量大约为10万，壁面的y+值在30左右。

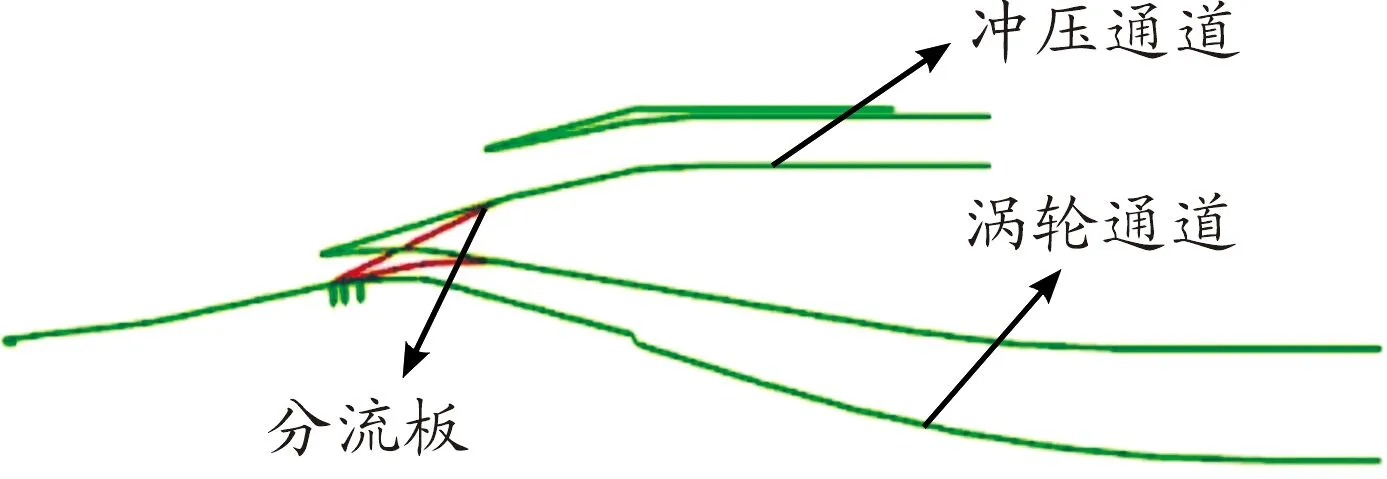
图1 进气道几何模型

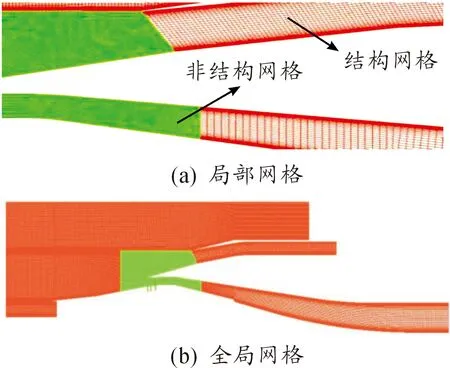
图2 进气道计算网格

2 不同模态转换时间的模态转换过程性能分析

对外并联进气道模态转换过程，涡轮通道由开到闭(正向模态转换)以及由闭到开(反向模态转换)在Ma2.1进行仿真分析。

2.1 涡轮通道全开和全闭稳定流场分析

首先对涡轮通道完全打开和完全关闭两种状态进行稳态数值模拟，以作为模态转换过程非稳态计算的初场。当涡轮通道全开时，冲压通道处于起动状态，如图3(a)，唇口斜激波打在下壁面，在冲压通道内形成反射波，冲压通道内主流均为超声速。当涡轮通道全关时，冲压通道由起动变为不起动，如图3(b)，在唇口处出现溢流脱体激波，冲压通道主流产生亚声速流，在冲压通道下壁面处产生厚边界层，且分流板产生的斜激波强度变大。此时的情况与文献[4]中出现的情况一致在涡轮通道全部关闭时，在冲压通道处出现溢流导致冲压通道不起动。

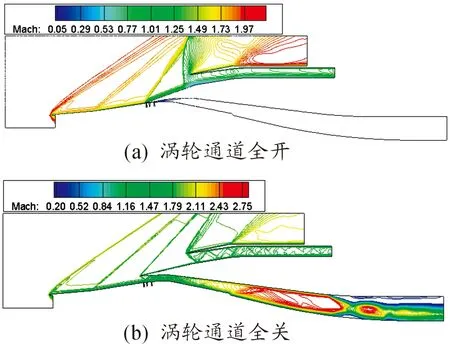
图3 涡轮通道全开和全关的等马赫图

2.2 模态转换时间为100 ms时进气道流场分析

分流板围绕后边的转轴逆时针旋转，涡轮通道由开到闭一共转动7.2°，用时100 ms,在整个模态转换过程每隔10 ms截取一个流场图。涡轮通道关闭10%到涡轮通道全关的等马赫线图如图4所示，涡轮通道关闭10%到50%，冲压通道起动，随着分流板向下转动，冲压通道内反射波消失，马赫数逐渐减小，分流板产生的斜激波的强度逐渐增大，从图4(a)-图4(c)可以看出涡轮通道关闭10%到30%的流场图相似，在涡轮通道关闭40%时，冲压通道内开始产生亚声速流，此时的冲压通道内既有超声速流也有亚声速流，当涡轮通道关闭50%时，此时唇口激波强度明显增强，冲压通道内产生较多的亚声速流，可以认为此时冲压通道刚好处于临界起动状态。

在涡轮通道关闭60%时，唇口截面前出现溢流脱体激波，冲压通道进入不起动状态，随着涡轮通道逐渐关闭，溢流激波强度逐渐增强，从图4(h)-图4(j)可以看出涡轮通道关闭80%到全关的流场图类似，此时的三道斜激波马赫数较大。

反向模态转换，分流板围绕后边的轴点顺时针旋转,涡轮通道关闭90%到涡轮通道关闭10%时的等马赫图如图5所示，冲压通道在整个过程均处于不起动，在涡轮通道关闭90%到涡轮通道关闭60%，唇口处有溢流激波，随着涡轮通道逐渐打开，溢流激波强度逐渐变弱并逐渐靠近唇口截面,第三道斜激波的强度逐渐变弱，冲压通道下壁面的边界层逐渐变薄，在此过程中冲压通道内都产生的都是亚声速流。涡轮通道全开时，如图5(j),冲压通道起动。

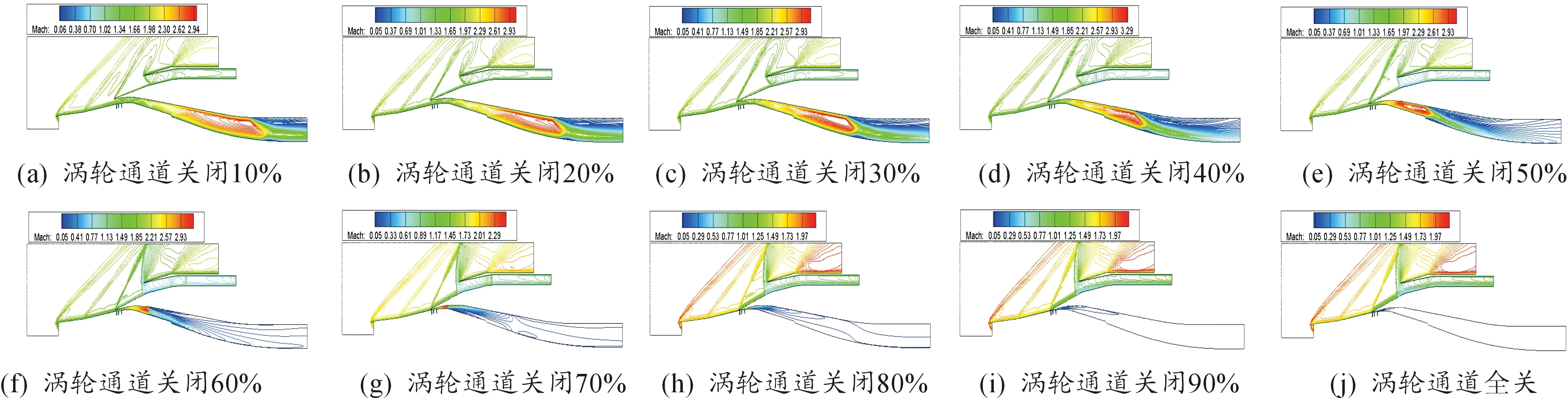
图4 正向模态转换涡轮通道不同开度等马赫图

图5 反向模态转换涡轮通道不同开度等马赫图

2.3 模态转换时间为50 ms时进气道流场分析

模态转换时间为50 ms时，涡轮通道关闭10%到涡轮通道全关闭的等马赫线图如图6所示，涡轮通道关闭10%到60%，冲压通道起动，随着分流板向下转动，冲压通道内反射波消失，马赫数逐渐减小，分流板产生的斜激波的强度逐渐增大，从图6(a)-图6(c)可以看出：涡轮通道关闭10%到30%的流场图相似，在涡轮通道关闭40%时，冲压通道内开始产生亚声速流，此时的冲压通道内既有超声速流也有亚声速流，涡轮通道关闭50%时的流场图与模态转换时间为100 ms时，涡轮通道关闭40%时的流场图相似，当涡轮通道关闭60%时，唇口激波强度明显增强，冲压通道内产生较多的亚声速流，可以认为冲压通道刚好处于临界起动状态。

在涡轮通道关闭70%时，唇口截面前出现溢流脱体激波，冲压通道进入不起动状态，随着涡轮通道逐渐关闭，溢流激波强度逐渐增强，从图6(h)-图6(j)可以看出：涡轮通道关闭80%到全关的流场图类似，此时的三道斜激波马赫数较大。与模态转换时间100 ms相比，进气道由起动状态变成不起动状态时涡轮通道处于的关闭状态百分比延迟，并且在涡轮通道关闭相同百分比时，涡轮通道的激波位置更靠后。

模态转换时间为50 ms时，涡轮通道关闭90%到涡轮通道全开时的等马赫图如图7所示，冲压通道在整个过程均处于不起动，在涡轮通道关闭90%到涡轮通道关闭40%，唇口处有溢流激波，随着涡轮通道逐渐打开，溢流激波强度逐渐变弱并逐渐靠近唇口截面,第三道斜激波的强度逐渐变弱，冲压通道下壁面的边界层逐渐变薄，在此过程中冲压通道内都产生的都是亚声速流。

2.4 模态转换时间为1 s时进气道流场分析

模态转换时间为1 s时，外并联TBCC进气道进行正向模态转换，涡轮通道关闭10%到涡轮通道全关的等马赫线图如图8所示，涡轮通道关闭10%到30%，冲压通道起动，随着分流板向下转动，冲压通道内反射波消失，马赫数逐渐减小，分流板产生的斜激波的强度逐渐增大，在涡轮通道关闭30%时，冲压通道内开始产生亚声速流，此时的冲压通道内既有超声速流也有亚声速流。

在涡轮通道关闭40%时，唇口截面前出现溢流脱体激波，冲压通道进入由起动状态变成不起动状态，随着涡轮通道逐渐关闭，溢流激波强度逐渐增强，冲压通道下壁面附面层逐渐增多，从图8(h)-图8(j)可以看出：涡轮通道关闭70%到全关的流场图类似，此时的三道斜激波马赫数较大。与模态转换时间100 ms相比，进气道由起动状态变成不起动状态时涡轮通道处于的关闭状态百分比提前，且没有临界起动状态，并且在涡轮通道关闭相同百分比时，涡轮通道的激波位置更靠前。

模态转换时间为1 s时，外并联TBCC进气道进行反向模态转换,涡轮通道关闭90%到涡轮通道全关的等马赫图如图9所示，在涡轮通道关闭90%到80%，冲压通道在整个过程均处于不起动，在涡轮通道关闭90%到涡轮通道关闭60%，唇口处有溢流激波，随着涡轮通道逐渐打开，溢流激波强度逐渐变弱并逐渐靠近唇口截面,第三道斜激波的强度逐渐变弱，冲压通道下壁面的边界层逐渐变薄，在此过程中冲压通道内都产生的都是亚声速流。在涡轮通道关闭10%时，在唇口处产生斜激波，进气道由不起动变为起动，与模态转换时间为100 ms相比，进气道由不起动状态变起动状态的涡轮通道关闭百分比提前，且在涡轮通道关闭相同百分比时，涡轮通道的激波位置更靠后。

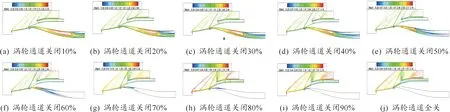
图6 正向模态转换不同开度等马赫线图

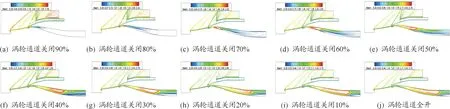
图7 反向模态转换涡轮通道不同开度等马赫图

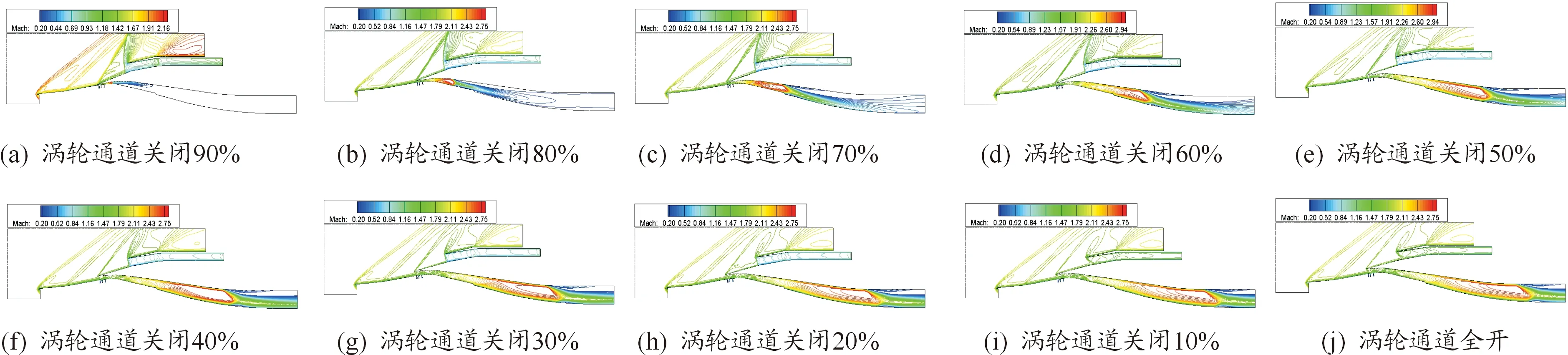
图9 反向模态转换涡轮通道不同开度等马赫图

2.5 模态转换时间对进气道性能参数的影响

不同模态转换时间下的冲压通道的出口总压恢复、流量系数以及出口马赫数如图10所示，正向模态转换涡轮通道全关到涡轮通道关闭60%，此过程模态转换时间为50 ms时，冲压通道起动；涡轮通道全关到涡轮通道关闭50%，此过程模态转换时间为100 ms时，冲压通道起动；涡轮通道全关到涡轮通道关闭30%，此过程模态转换时间为1s时，冲压通道处于起动状态这个过程内，随着涡轮通道逐渐关闭，冲压通道的出口总压恢复略有升高流量系数逐渐增大出口马赫数逐渐降低，并且模态转换时间越长，出口总压恢复越小而流量系数越大。在涡轮通道进一步关闭到30%,50%以及60%时，三个不同模态转换时间的冲压通道流量系数、总压恢复分别发生突降，冲压通道由起动变为不起动，并且随着涡轮通道进一步关闭，不起动状态加剧，冲压通道出口总压恢复和流量系数进一步减小。

反向模态转换过程中，模态转换时间为50 ms时涡轮通道由全闭到全开时，模态转换时间为100 ms时涡轮通道由全闭到关闭10%，模态转换为1s时涡轮通道由全闭到关闭20%，总压恢复和流量系数均处于较低水平，冲压通道处于不起动状态。模态转换时间为100 ms时，涡轮通道关闭10%到涡轮通道全开以及模态转换时间为1 s时涡轮通道关闭20%到涡轮通道全开，冲压通道由不起动变为起动，在此过程内，出口总压恢复和出口马赫数明显增大，冲压通道处于不起动时出口马赫数变化不大,在1.11到1.13范围内变化。

由以上分析看出：对于正向模态转换，模态转换时间越短，冲压通道由起动变不起动状态时的涡轮通道关闭越多，冲压通道越不容易从起动变不起动；而反向模态转换正好相反，模态转换时间越长，冲压通道越容易从不起动变起动。

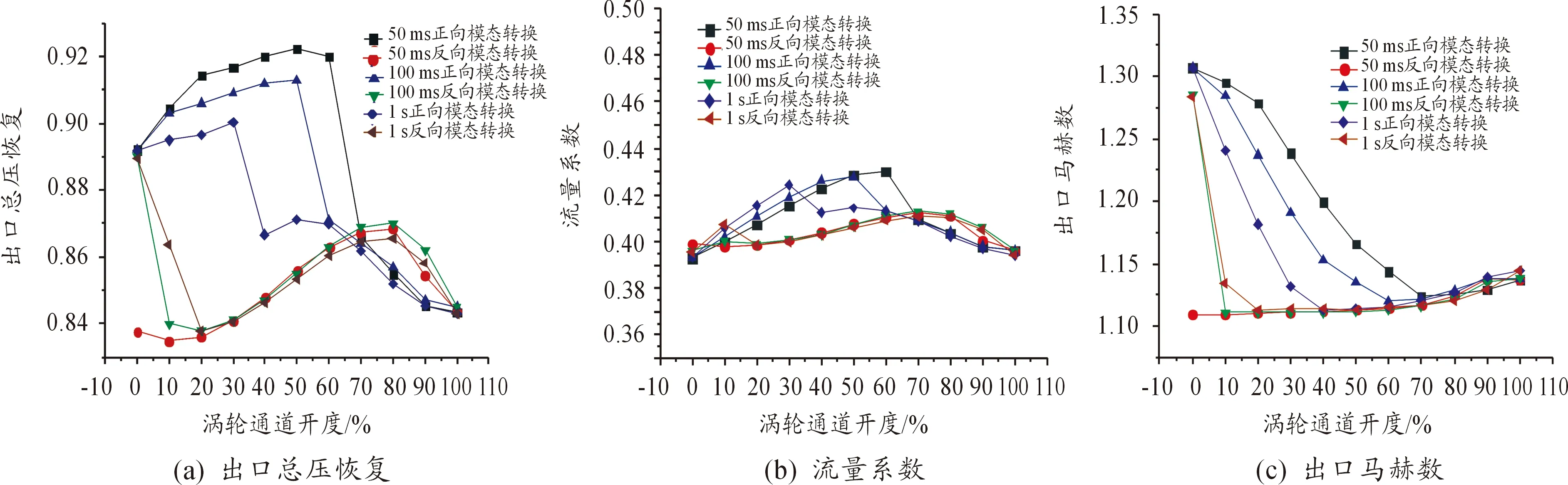
图10 模态转换过程性能参数变化

3 结论

1) 正向模态转换模态转换时间为50 ms时在涡轮通道关闭70%，模态转换时间为100 ms时在涡轮通道关闭60%，模态转换时间为1s时在涡轮通道关闭40%，冲压通道由起动变为不起动，模态转换时间越短，冲压通道处于不起动状态的范围越小。

2) 反向模态转换过程，模态转换时间为50 ms时，整个过程均处于不起动状态；模态转换为100 ms时，在涡轮通道关闭10%时，冲压通道由不起动变起动；模态转换为1 s时，在涡轮通道关闭20%时，冲压通道由不起动变起动，模态转换时间越长，冲压通道处于起动状态的范围越大。