时间误差对预警机协同制导导弹的影响

李美红,乔永杰,杨 喆

(中国电子科学研究院， 北京 100041)

在现代超视距空战中，通常由预警机为作战平台提供远距离目标信息，并引导作战平台进行武器发射，以完成协同作战任务。美国NIFC-CA系统将航母、舰船、舰载机等作战单元进行无缝联接，构成一体化打击体系，探测平台对目标进行火控级的跟踪，并将高精度的目标信息在各平台之间共享，传感器和武器系统直接交联并进行协同作战。然而网络化作战体系中，不同作战平台之间不可避免地存在时间同步误差和信息传输时延，从而对多平台协同作战产生严重影响，需要进行深入研究。

文献[1-3]研究了双机协同攻击时的指令瞄准建模与精度、指令修正惯性中制导方法和预警机-战斗机-导弹的打击链模型；文献[4]研究了硬件在回路仿真中不可避免的时间延迟效应，以及数字控制器和硬件在回路的仿真器之间的时间延迟量；文献[5]研究了中远程红外末制导导弹的制导信息的周期指标，按照红外导引头探测性能给出了数据链周期的确定原则；文献[6]研究了目标指示信息延迟对反舰导弹末制导雷达参数装订的影响；文献[7]分析了影响直升机载空空导弹中末交接时截获概率的主要误差源及其影响。而关于时间误差对预警机协同制导空空导弹的中末制导交接影响研究较少，本文以预警机引导战斗机发射远程空空导弹为例，分析协同作战过程中各阶段的时间误差特性，及其造成的导弹中制导段末端散布误差、目标信息误差和导引头指向误差，通过仿真计算导引头截获概率随时间误差的变化情况，从而确定协同制导过程中时间误差的允许范围。

1 预警机协同制导过程

“预警机-战斗机-导弹”形成打击链，进行协同作战的概念如图1所示。

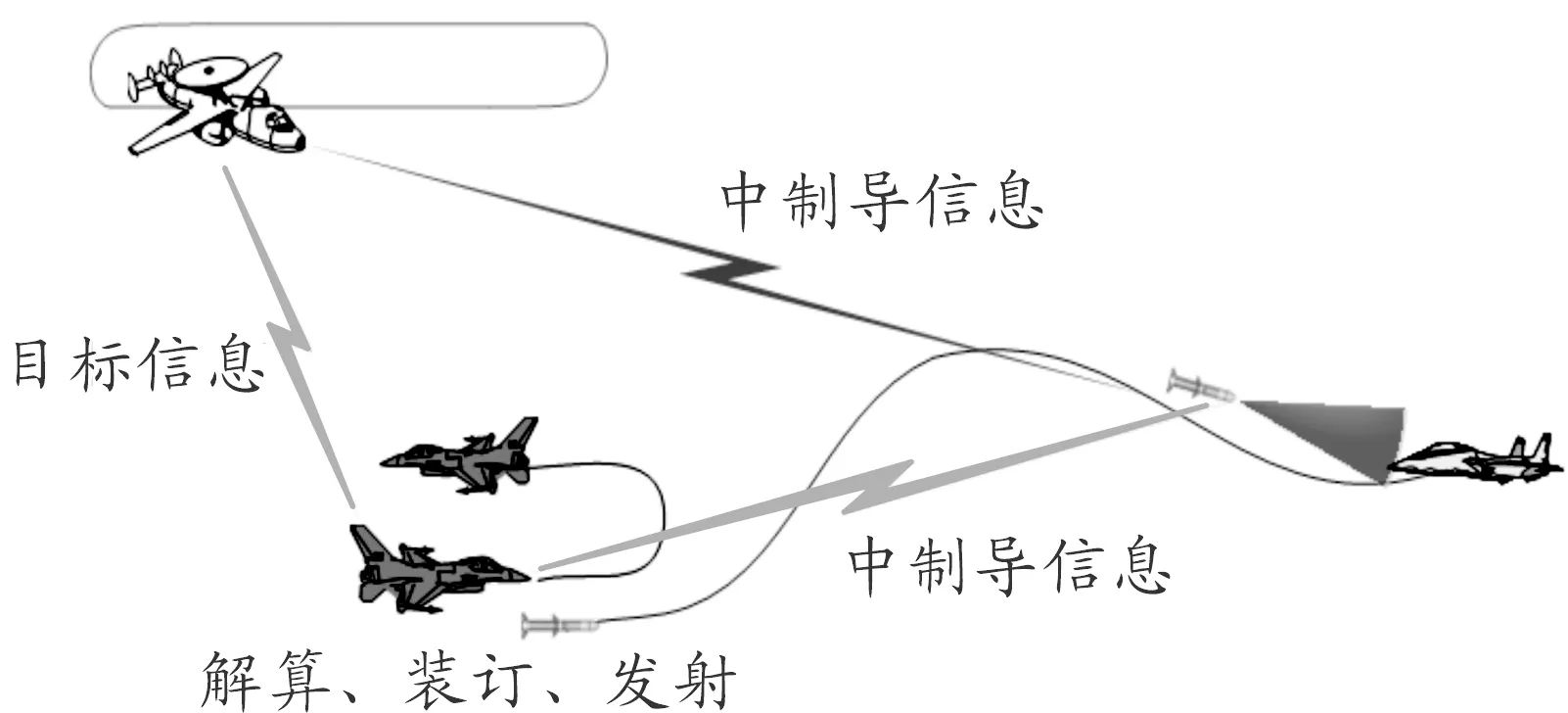
图1 预警机协同制导远程空空导弹打击链

首先，预警机对远距离目标进行探测识别，确定为敌方目标后，将计算得到的目标位置、速度、方向等信息，通过机间数据链发送给战斗机；然后，战斗机根据目标信息进行解算，满足发射条件时将目标参数装订到导弹，进入攻击区后发射导弹，并将导弹的初始信息上传到预警机。预警机继续为战斗机提供远程目标指示，或直接与导弹建立通信进行协同制导。导弹在发射后的初始段按程序控制飞行；中段根据接收到的目标信息按预定的导引律飞行，到达中末段制导交接点附近，或满足导引头最大探测距离时，导引头开机搜索，捕获目标后进入末制导，导弹按设定的制导律飞行，直到命中目标。

2 时间误差模型

预警机引导战斗机发射导弹的过程中，涉及的时间误差如图2所示。

2.1 时间同步误差

预警机与战斗机协同作战之前必须先进行时间统一，将两平台及各自分系统的信息统一到同一时间基准，以确保后续准确有效的导弹发射和协同制导。

协同作战的预警机和发射平台，通过自同步和时延测量、实时校准及高稳度时钟源等方法进行时间同步，或采用战术数据链以往返计时报文的方法进行时间同步，精度可达μs级。

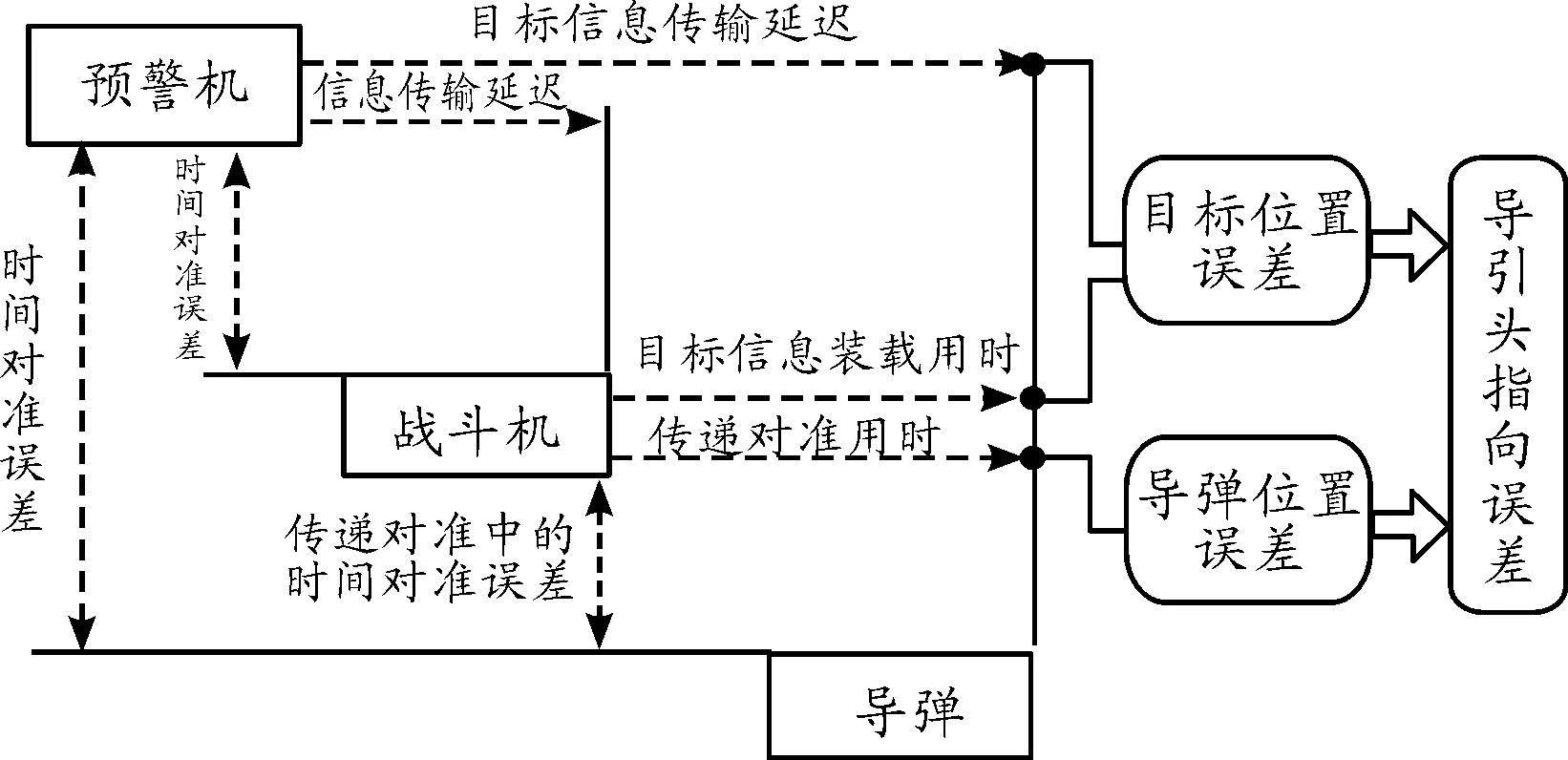
图2 打击链中的时间误差模型

导弹发射前，载机与导弹进行传递对准，其中包含时间对准项的内容，该项信息存在误差；又由于机载惯性导航系统的参数一般先传给机载火控系统进行信息处理，再传给弹载惯性导航系统，使得传递对准这一过程消耗一定的时间，进一步增大了载机与导弹的时间同步误差。

如果预警机直接制导导弹，两者需建立时空基准，但不可避免地存在一定的时间同步误差。预警机向导弹发送的目标信息包含时间戳信息，但前提是两者之间已进行时间对准，或已知两者之间的时间同步误差。

从预警机探测目标一直到导弹离机，主要的时间延迟项如表1所示，总时延为∑τi。

3 截获概率计算

3.1 导弹位置误差

弹载惯性导航系统具有一定的测量误差，其测量误差随时间积累而增大，导致导弹所测自身位置参数存在误差，中制导段末端的导弹定位误差ΔPm为：

ΔPm=(Δxm,Δym,Δzm)=Vf(ta+tIa)+tf·δm

(1)

式(1)中，Vf为飞机在传递对准时的速度；δm为弹载惯性导航系统的定位精度；tIa为初始对准中时间对准项信息的误差；ta为传递对准过程消耗的时间；tf为导弹飞行时间。

导弹位置估计误差的方差为：

(2)

3.2 目标位置误差

如果预警机为战斗机提供目标指示，可能的最大时延为表1中各时延项之和；如果预警机直接制导导弹，可能的最大时延为两者之间的时间同步误差，与信息传输周期、发送和接收时延之和。如果在信息延迟时间td内目标进行机动，将产生目标位置误差；对目标的机动估计误差，计算如下[8]：

(3)

式(2)中，nt为目标过载；vt为目标速度。目标位置估计误差的方差可表示为：

(4)

表1 时间延迟项

3.3 截获概率模型

空空导弹在中末段制导交接时，导引头截获目标包括角度截获、距离截获和速度截获，距离截获要求弹目距离小于导引头最大探测距离，角度截获要求目标实际位置处在导引头的视场角范围。导弹在中、末制导交接时，目标指示误差如图3所示，中制导结束时导弹弹体纵轴指向Ox方向，导引头轴线指向Rs(图中虚线表示导引头视场)，与弹体纵轴的夹角Φ为目标指示角。目标相对导弹的视线为Rm，则Rs与Rm的夹角Φa即为目标指示角度误差[9]。设导引头波束宽度为±λ，如果Φa<λ，则认为是导引头角度截获目标。

将目标指示误差Φa在导引头平台系的Oxsyszs内投影，得到在导引头视线坐标系上，导引头目标指示误差在Oys、Ozs轴上的分量Φey、Φez，假设随机变量Φey、Φez服从均值为零的正态分布，其概率密度函数分别为：

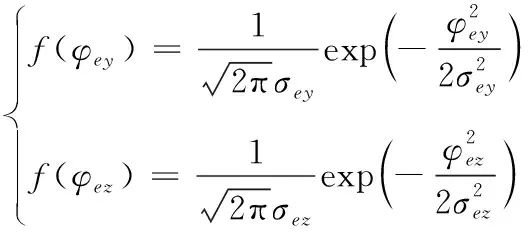
(5)

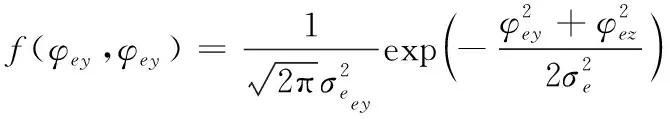
(6)

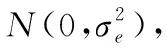
(7)

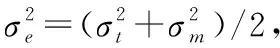
(8)

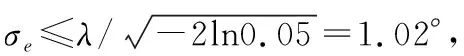
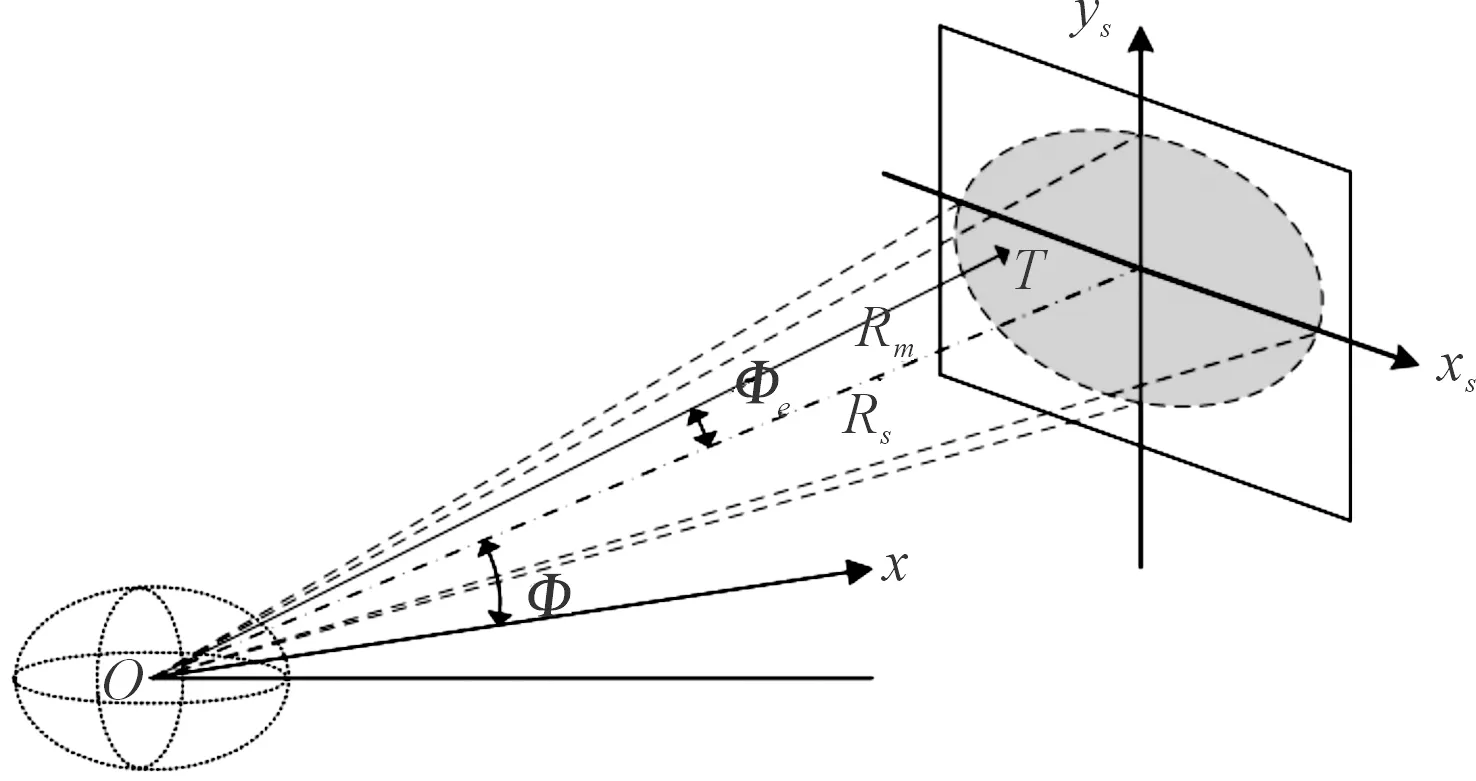
图3 导引头指示误差示意

4 仿真分析

4.1 仿真条件

设目标的初始位置为(300 km,50 km,10 km)，初始速度为(-270 m/s，0 m/s，0 m/s)，在发现威胁前作匀速直线运动；发现威胁后立即进行机动规避，目标加速度可达20 m/s2，目标飞机的最大过载为8。导弹平均速度设为400 m/s，弹道倾角为θ=0.38°，偏航角为ψ=9.5°，导弹发射离机后1～2 s后进入程序控制阶段，中段采用比例导引，比例导引系数选为3，末段采用主动雷达寻的制导，导引头波束宽度5°，探测距离为30 km。

4.2 结果分析

4.2.1 目标未发现威胁

理想情况下，假设敌机未发现威胁，保持匀速飞行。如图4所示，导弹飞行约163 km后，到达攻击区附近，敌机进入导引头最大探测范围时，导引头开机，可见目标散布范围基本落在导引头搜索区域内，满足导弹顺利转入末制导的条件。

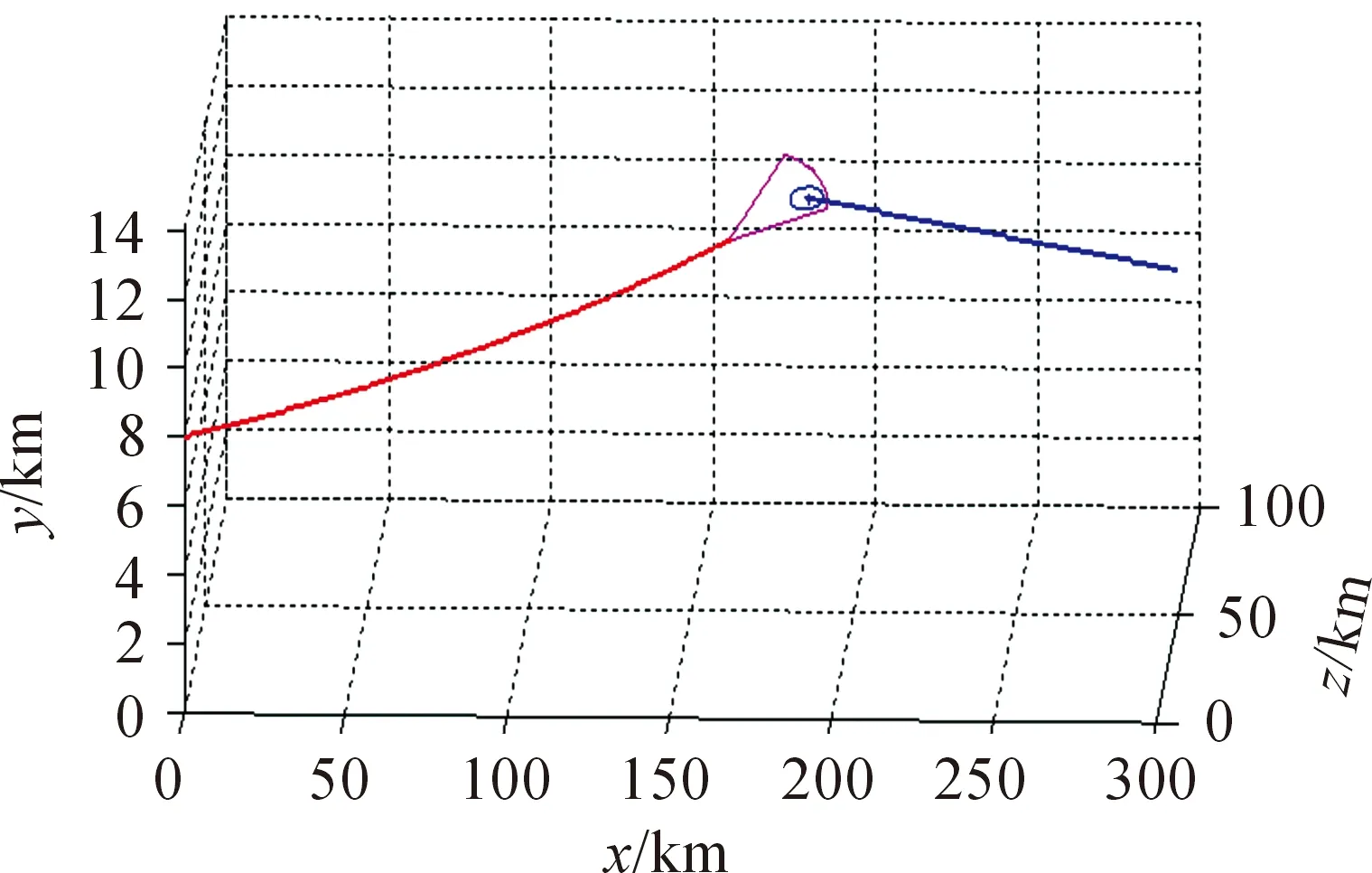
图4 目标未发现威胁时的弹道

4.2.2 目标发现威胁

假设目标在导弹距其50 km时发现威胁，立即采用横向转弯进行规避，如图5所示，可见目标位于导引头搜索区域边缘，截获概率降低，不能保证导弹顺利转入末制导。

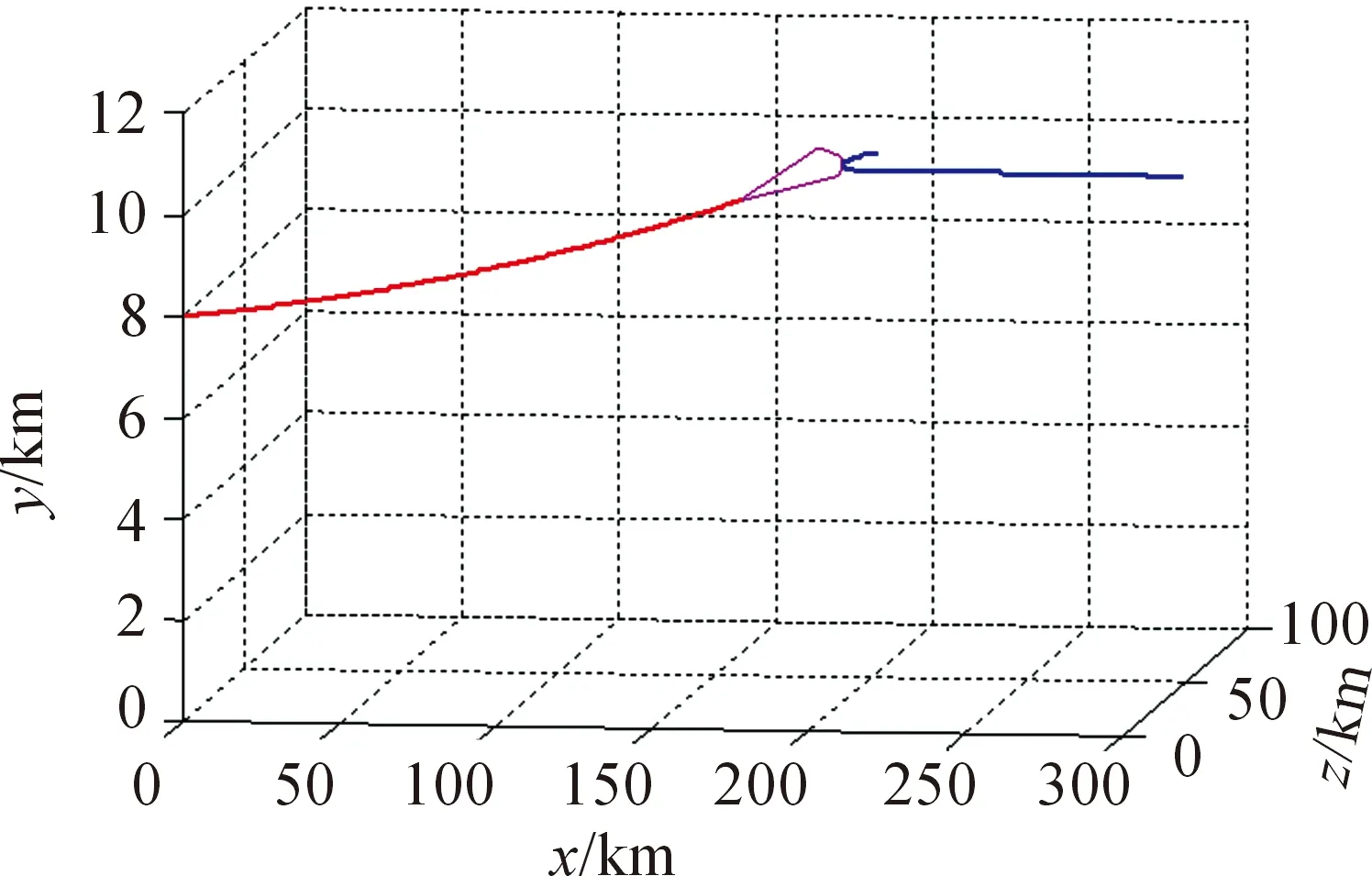
图5 目标加速转弯机动时的弹道

将初始设置参数代入公式，可得时间误差和导引头截获概率的关系，如图6所示。

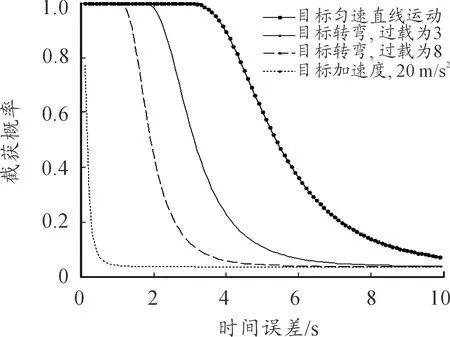
图6 时间误差对导引头截获概率的影响

由图6可见，若目标未发现来袭导弹并一直做匀速运动，无时延时导引头对目标的截获概率为99.9%；时延为3.7 s时导引头截获概率为95.4%，截获概率随时间误差增大到而降低，时延为4 s时降低到89.4%；若目标发现威胁后以8 g过载进行转弯，时延为1.4 s时导引头截获概率为90.8%，小于要求的截获概率95%；若目标通过加速并转弯进行规避，时延为0.1 s时截获概率就降低到80%以下，与图5中的弹道仿真结果吻合，可见目标做大机动时，时间误差将直接影响导弹转入末制导，降低命中概率。

5 结论

1) 如果敌机探测能力较弱，同时我方提高隐身性能，使敌机难以发现威胁，时间误差小于4 s可基本满足转入末制导的条件。2) 如果敌机的探测能力较强，发现威胁后进行转弯机动，时间误差需限制在2～3 s；目标具有很高的机动性时要求时间精度达到秒级，由于较难命中，需考虑多弹多次拦截等其他战术。3) 通过给定的初始条件，可计算时间误差对导引头截获概率的影响；同时可根据截获概率的要求，确定系统的时间精度指标。实际作战中还存在坐标转换误差，考虑时空一致性的影响以及对协同制导过程中的时间误差进行分配，将是下一步研究重点。