一类具有时变和分布时滞的神经网络系统的时滞相依全局稳定性分析

毛 凯，孙校书，杨树杰，刘 丹，宋玮玮

（1.海军航空大学，山东 烟台264001；2.烟台大学文经学院，山东 烟台264000）

由于在诸如图像处理、模式识别、联想记忆以及优化问题等方面的应用和潜在应用，近年来，神经网络系统得到了广泛的研究[1-2]。众所周知，神经网络系统的应用极大地依赖于其动力学行为，尤其是其平衡点的存在性和稳定性。同时，由于放大器转换速度的有限和信息处理速度的有限，时滞现象在神经网络系统中往往是不可避免的，时滞也常使得系统不稳定或产生振荡。因此，时滞神经网络系统的稳定性研究在理论和实践中都具有重要意义，已有不少关于时滞神经网络系统时滞相依或时滞独立的稳定性研究结果[3-6]。一般说来，时滞相依稳定性结果中包含了时滞的信息，因而通常比时滞独立的稳定性结果具有更低的保守性，尤其是对于小时滞神经网络系统来说这种现象更为明显。也正因为如此，使系统达到全局稳定的时滞最大可能取值——时滞最大允许上界（MAUB）成为学者们极其关注的研究指标，MAUB同时也是系统稳定性条件具有更低保守性的标志性指标，这方面的研究成果也不断被提出。然而，人们已经认识到，传统的Lyapunov-Krasovskii泛函的构造对系统稳定性条件保守性的降低作用甚小。因此，增广Lyapunov-Krasovskii泛函的构造就成为降低系统稳定性条件保守性的必然选择之一[7]。

近年来，时滞分割逐渐成为降低保守性的有效手段之一，例如，具有定常时滞的神经网络系统[8]，具有时变时滞的神经网络系统[9-13]，以及具有多时滞成分的连续系统[14]，离散系统[15]以和一类中立型时滞系统[16]，都利用了时滞分割技术获得系统的全局稳定性条件。文献[17]基于时滞分割技术研究了一类具有分布时滞的线性分数阶不确定性系统的稳定性及鲁棒稳定性问题，文献[18]首次将这种方法扩展至同时具有离散和分布时滞的中立型系统的稳定性研究。尽管上述文献的稳定性结果已具有较低的保守性，但通过构造恰当的增广Lyapunov-Krasovskii泛函，并使用更好的定界技巧估计泛函导数的上界，可望获得比上述文献具有更低保守性的系统稳定性结果。

基于以上分析，本文首先构造一个新的增广Lyapunov-Krasovskii泛函；再利用时滞分割技术对时变时滞函数的下界、定常分布时滞进行不同分割，并借助自由权矩阵和Jensen积分不等式等手段对泛函导数的上界进行更精细的估计、定界，获得以LMIs形式描述的具有更低保守性的系统时滞相依全局渐近稳定性判定条件；最后，以数值实例说明了方法的有效性。本文中：ℝn×m表示n×m实矩阵空间；上标T表示转置；X≥Y（X＞Y）表示X-Y半正定（正定），其中X、Y均为对称阵；In×n、0n×n分别表示n×n单位阵和零矩阵；记号∗表示对称矩阵中相应的对称块；sym(A)=A+AT；r表示分布时滞长。

1 问题描述

考虑如下同时具有时变和分布时滞的神经网络系统：

式（1）中：n为系统中神经元数目，y(t)=(y1(t),y2(t),…,yn(t))T为 神 经 元 状 态 向 量 ；g(y(t))=(g1(y1(t)),g2(y2(t)),…,gn(yn(t) ))T为神经元激励函数；C=diag(c1,c2,…,cn)为神经元自反馈系数矩阵；A,B,D∈ℝn×n分别表示神经元连接、时滞连接和分布连接矩阵；I=diag(I1,I2,…,In)为系统输入常向量；y(t)=ψ(t),-τ≤t≤0为初始条件。

一般，对激励函数和时变时滞函数作如下假设：

H2：时变时滞函数τ(t) 可微，且0＜τ1≤τ(t) ≤τ2，τ˙(t) ≤τ3＜1，其中τ1、τ2、τ3均为常数。

对于给定的初始条件，上面的假设H1保证了系统（1）平衡点y∗=(y1∗,y2∗,…,yn∗)的存在性，作平移变换xj(t)=yj(t)-yj∗，则系统（1）变为：

引理1（Jensen积分不等式）[9]：对任意的对称正定阵M=MT＞0，标量τ2＞τ1＞0及使得如下积分有定义的向量值函数ω:[0,γ]→ℝn，下面的积分不等式成立：

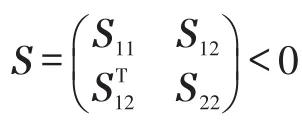
2 主要结果

本节将在一个新构造的增广Lyapunov-Krasovskii泛函的基础上，对时变时滞函数的下界和定常分布时滞同时进行时滞分割，以推导系统时滞相依全局稳定性条件。首先引入如下的记号：

定理1：对给定的τ1、τ2、τ3，正整数m,l≥1 ，若存在对称正定矩阵P∈ℝ3n×3n，Q1∈ℝmn×mn，Q2∈ℝln×ln，Q3∈ ℝ2n×2n，Z,Ri∈ ℝn×n(i=1,2,3,4 )，Si∈ ℝn×n(i=1,2)，非 负 对 角 阵W=diag(w1,w2,…,wn)，Δ=diag(δ1,δ2,…,δn)，Λi=diag(λi1,λi2,…,λin)，i=1,2 ，以及任意恰当维数的矩阵Mi、Ni、Fi、Gj（i=1,2;j=1,2,3），使如下LMIs（3）成立，则系统（2）的平衡点是全局渐近稳定的，

式中，Ξ定义为：

式（4）中：

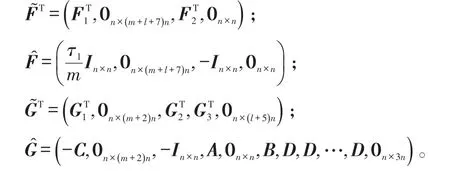
证明：由Brouwer不动点定理，不难证明系统平衡点的存在性，这里仅需证明平衡点的全局渐近稳定性。

为此，构造如下形式的增广Lyapunov-Krasovskii泛函V(t)=V1(t)+V2(t)+V3(t)+V4(t)。

式中：

现计算V(t)沿系统（2）对时间的导数，并进行适当的放大整理。

对于V˙3(t) 、V˙4(t)中如下的3个积分项，由引理1，有：

根据Newton-Leibniz公式及系统（2），对于恰当维数的矩阵Mi、Ni、Fi、Gj（i=1,2;j=1,2,3），总有如下的等式成立。

由关于激励函数的假设H1，对任意非负标量λij≥0,i=1,2;j=1,2,…,n，下面的不等式成立：

或由矩阵向量形式等价地描述为：

由式（5）～（20），经过一系列运算、整理，不难得到：

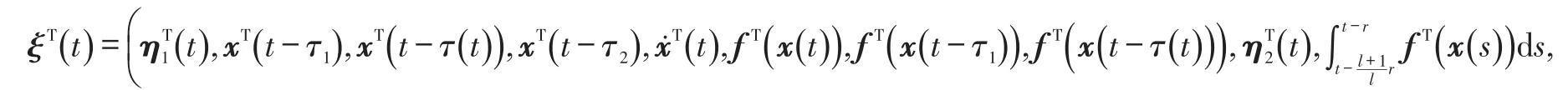
由系统（3）以及引理2易知，存在恰当的小正数ε，使得Σ＜diag(-εI,0,0,…,0 )，其中：

于是，有V˙(t)≤ξT(t)Σξ(t)＜-ε‖x(t)‖2。

这意味着时滞系统（2）的平衡点是全局渐近稳定的，证毕。

注1：正如前文所说，时滞分割技术被广泛应用于定常或时变的离散时滞系统，却很少应用于分布时滞系统。受文献[18]的启发，本文首次尝试将时滞分割技术推广应用于同时具有时变时滞和分布时滞的神经网络系统的稳定性分析。

注2：定理1中，稳定性条件保守性的降低得益于新构造的增广Lyapunov-Krasovskii泛函，其中不仅含有针对时变时滞和分布时滞的时滞分割积分项，也含有时滞分割的二重及三重积分项，如V2(t)中的前2个积分项，V3(t)中的前2个二重积分项和V4(t)中的三重积分项。

注3：在文献[20]中，Chen等通过构造含有一个Lyapunov-Krasovskii二重及三重积分项的增广泛函，未使用时滞分割技术研究了一类具有离散时滞的神经网络系统的稳定性条件。而基于时滞分割技术的新的Lyapunov-Krasovskii泛函却可以获得比已有文献结果具有更低保守性的系统稳定性条件。

注4：在文献[13]中给出了具有离散区间时滞和分布时滞的随机神经网络系统的指数稳定性条件，值得注意的是文中的分布时滞是时变的。本文虽然考虑的是定常分布时滞，但本文的方法能够推广到时变分布时滞系统上去，这也是近期将开展的工作。

下面将考虑系统（2）的2个特殊情形：

情形1：若τ(t)=τ，则经过平衡点平移变换后，相应的系统由下式给出

对上述系统构造Lyapunov-Krasovskii泛函

式中：

通过类似定理1的方法，容易得到如下推论。

推论1：对给定的τ、r，正整数m,l≥1，若存在对称 正定阵P∈ℝ3n×3n，Q1∈ℝmn×mn，Q2∈ℝln×ln，Q3∈ ℝ2n×2n，Ri∈ ℝn×n(i=1,2,3,4 )，Si∈ ℝn×n(i=1,2)，非负 对 角 阵W=diag(w1,w2,…,wn)，Δ=diag(δ1,δ2,…,δn)，Λi=diag(λi1,λi2,…,λin),i=1,2以 及 任 意 恰 当 维 数 的 矩 阵Mi、Ni、Fi、Gj（i=1,2;j=1,2,3,4）使如下的LMI成立，则系统（22）的平衡点全局渐近稳定，

式中，Σ定义为：

式（23）中：

情形2：若在系统（2）中令D=0，则经过平衡点平移变换后，相应的系统即为在很多文献中得到广泛研究的时变时滞神经网络系统：

相应地有关于系统（24）的如下推论。

推论2：对于给定的τ1、τ2、τ3，正整数m≥1，若存在对称正定阵P∈ℝ2n×2n，Q1∈ℝmn×mn，Q3∈ℝ2n×2n，Z,Ri∈ ℝn×n(i=1,2,3) ，S1∈ ℝn×n，非负对角阵W=diag(w1,w2,…,wn)，Δ=diag(δ1,δ2,…,δn)，Λi=diag(λi1,λi2,…,λin),i=1,2 ，以及任意恰当维数的矩阵Mi、Ni、Fi、Gj（i=1,2;j=1,2,3,4），使如下的LMIs成立，则系统（24）的平衡点是全局渐近稳定的，

式中，Π的定义为：

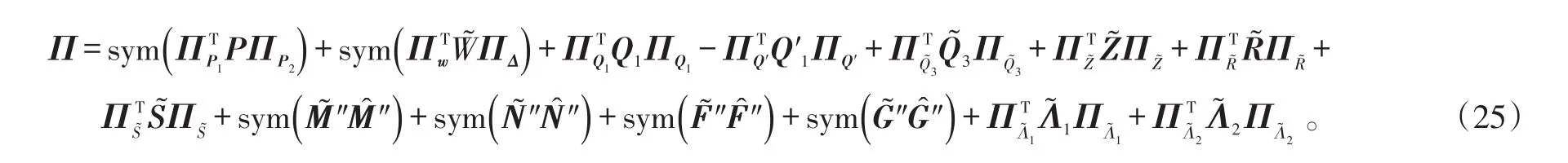
式（25）中：

3 数值实例

这里将给出2个数值实例，用本文方法计算结果，并与相关文献结果进行比较。

例1：考虑文献[18，20]给出的2阶时滞神经网络系统，相关参数如下：

根据由文献[20]稳定性判据得到的时滞最大允许上界为6.827 9；当m、l分别都取相等的1、2、3、4时，文献[18]给出的相应结果分别为5.514 7、7.236 8、8.582 6和9.724 5。而用本文推论1的结论，当m、l分别都取相等的1、2、3、4时，相应的结果则为6.846 1、7.257 9、8.697 4和9.752 3。显然，本文结果相较于文献[18，20]的结果具有更低的保守性。

例2：考虑文献[21-24]中给出的2阶时滞神经网络系统，相关参数如下：

为与已有文献结果进行比较，设τ1=0，τ3=0.6，则τ2的MAUB分别为2.921 9[24]、2.933 4[23]。而用本文推论2的结论，当时滞分割数m分别取1、2、3、4时，τ2的MAUB分别为2.965 1、2.997 4、3.011 2和3.120 7。

尽管时滞分割能降低系统稳定性条件的保守性，但必须指出的是，随着时滞分割数m或r的增加，保守性的降低将越来越不明显，而计算的复杂程度却越来越高。在实际应用中，应当兼顾保守性和计算复杂度，尽量选取适当的时滞分割数。

4 结语

本文基于时滞分割技术研究了一类同时具有时变时滞和分布时滞的神经网络系统的全局稳定性，通过对时变时滞函数的下界和定常分布时滞进行时滞分割并构造一个新的增广Lyapunov-Krasovskii泛函，获得系统一个改进的时滞相依全局渐近稳定性充分条件，时滞分割是降低稳定性条件保守性的关键因素。保守性随着时滞分割数目的增加而降低，但降低幅度越来越小。稳定性条件是以LMIs给出的，便于使用标准的数字软件包加以检验，数值实例清晰表明时滞分割技术可以有效地降低稳定性条件的保守性。