基于短时分数阶傅里叶变换的含噪信号特征提取

郝田义，薛永华，郑志刚

（1.中国飞行试验研究院，西安710089；2.海军航空大学，山东 烟台264001；3.上海久航电子有限公司，上海610092）

短时傅里叶变换作为一种较为成熟的时频分析工具，由于其运算快捷，时频分辨率较高，且无交叉项干扰而倍受研究学者的青睐[1-5]。但是短时傅里叶变换在处理调频信号时随着信号调频率变化率的增大，在时频分辨率上会变得模糊。

在信号处理中，当利用短时傅里叶变换对调频信号进行瞬时频率估计时，就有可能出现估计精度不高的问题。而将分数阶傅里叶变换（Fractional Fourier Transform，FRFT）[6-9]引入短时傅里叶变换后得到的短时分数阶傅里叶变换（STFRFT）[10]，由于将非线性调频信号进行短时截取，当窗函数选择合理时，截取后的每一段区间信号可以近似看作线性调频信号，利用分数阶傅里叶变换对线性调频信号的高度时频聚集性，可以较为容易地获得非线性调频信号的高时频分辨结果。因此，短时分数阶傅里叶变换可以起到提高非线性调频信号时频估计精度的效果[10-19]。因此，本文从噪声背景下短时分数阶傅里叶变换的时频分辨能力仿真分析入手，研究了短时分数阶傅里叶变换滑窗口方式与瞬时频率估计的关系。

1 时频分辨能力

1.1 理论

分数阶傅里叶变换定义式为[6]：

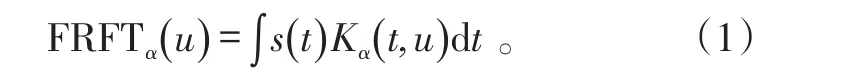
式（1）中：α为变换角度；Kα(t,u)为变换核。

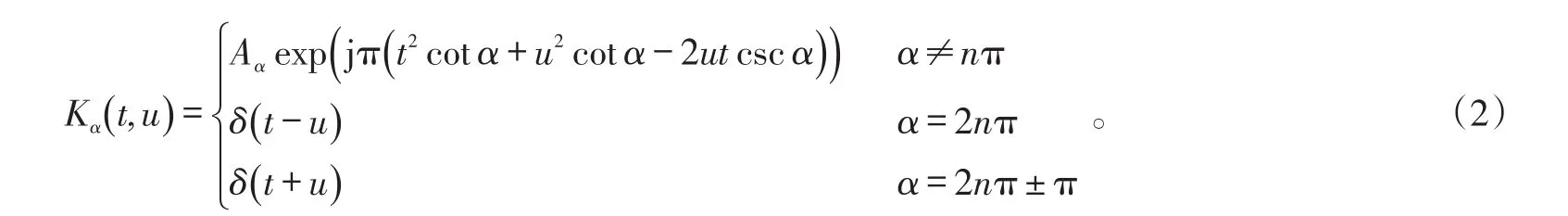
FRFT是传统傅里叶变换的广义形式。利用FRFT的这一特点，对短时傅里叶变换进行广义化，可以得到STFRFT，其定义式为[10]：

1.2 仿真

仿真信号为：

式（4）中：初始频率f0；采样时间为1 s；采样频率为1 024Hz；窗函数采用高斯窗，窗长为0.125 s；滑动步长为1个采样周期；N(t)为均值为0的高斯白噪声，信噪比为-4dB，分别对信号进行含噪情况下的短时傅里叶变换和短时分数阶傅里叶变换，提取的时频分析谱图如图1所示。

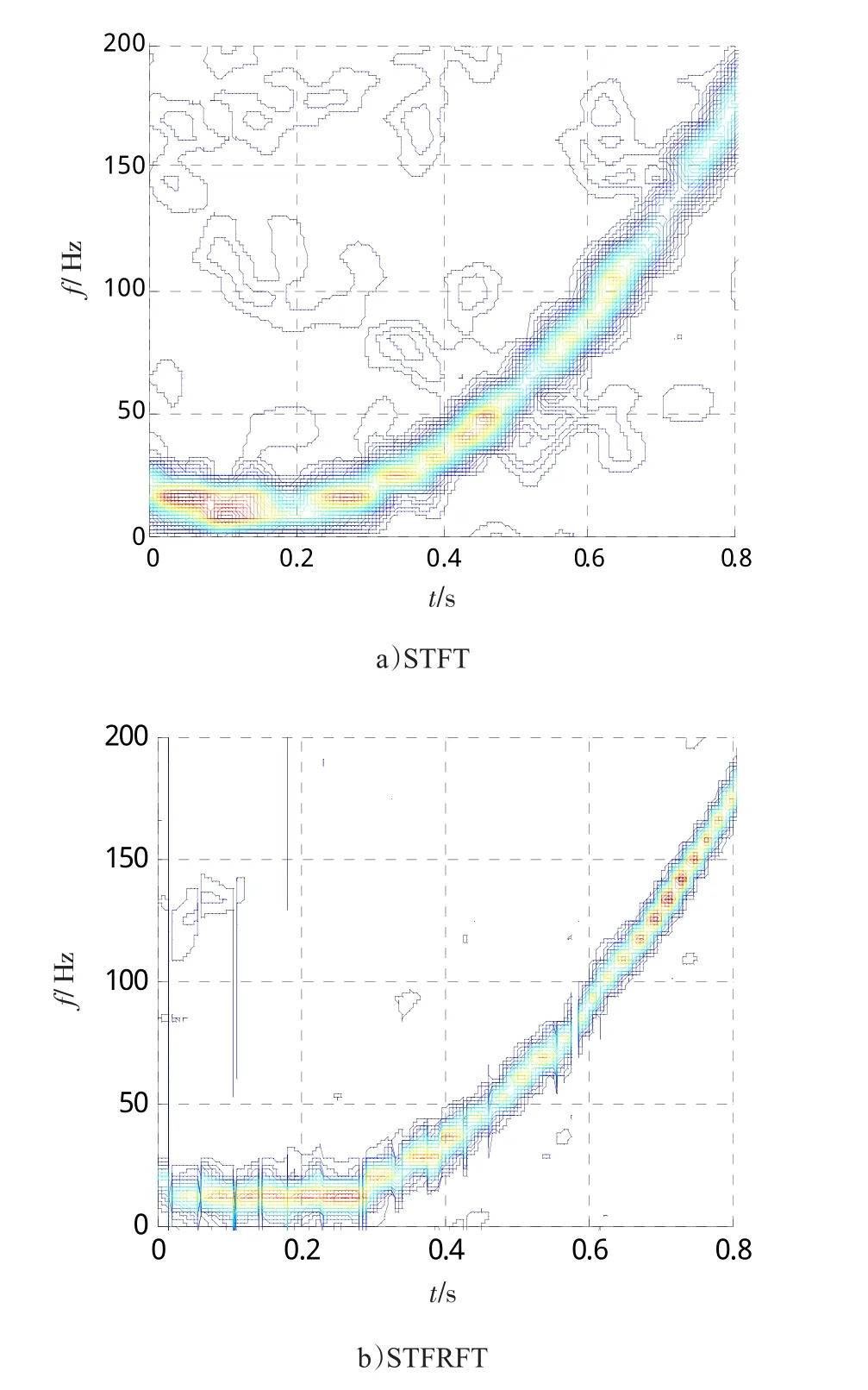
图1 SNR=-4dB条件下STFRFT与STFT的时频分辨能力对比Fig.1 Time-frequency resolution comparison between STFRFT and STFT withSNR=-4dB

从图1中可以看出，在信噪比为-4dB时，STFT和STFRFT都还能够保持良好的时频聚集性，但较高的聚集性主要体现在频率变化率较低的部分（如图1中的0～0.2 s）。在频率变化率较高的时间段（如图1中的0.6～0.8 s），STFT的能量峰值有所减弱，时频聚集性减弱，而STFRFT在频率变化率较高的时间段，时频聚集性仍然保持较好。纵观整个时频谱图，由于STFRFT的良好鲁棒性，使得待测信号在含噪声条件下仍然能够获得很好的能量聚集性，反映在时频谱图中的噪点更少。由此可知，STFRFT在抗噪声性能方面比STFT更为出色。

2 基于STFRFT的瞬时频率估计的滑窗方式分析

对于非线性调频信号在经过短时分数阶傅里叶变换时，可以认为其在短时窗内是近似线性调频信号，如图2所示，以此实现对非线性调频信号的瞬时频率估计[13]。

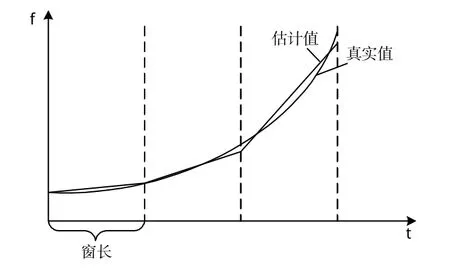
图2 STFRFT对非线性调频信号的瞬时频率估计Tab.2 Instantaneous frequency estimation of non-linear FM signal using STFRFT

2.1 滑动方式选择

在进行短时分数阶傅里叶变换的过程中，为获得某一采样时刻的瞬时频率估计值，需要将短时窗沿时间轴进行滑动。对于短时分数阶傅里叶变换，其短时窗滑动可以有以下3种不同方式。采用不同的滑动方式将会导致不同的瞬时频率估计效果。

1）无重叠滑动方式。当采用无重叠滑动的方式进行瞬时频率估计时，窗函数在整个时间段内每次滑动一个窗长，各窗长之间不发生重叠。每进行一次滑动，通过在短时窗内进行的分数阶傅里叶变换就会相应的得到该时间段内的一组瞬时频率估计值：

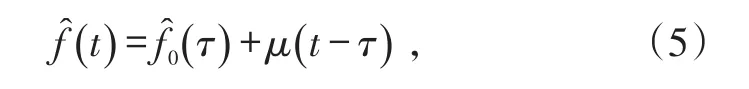
式中，τ为短时窗的初始时刻，由此可以得到每个采样时刻的瞬时频率估计值。

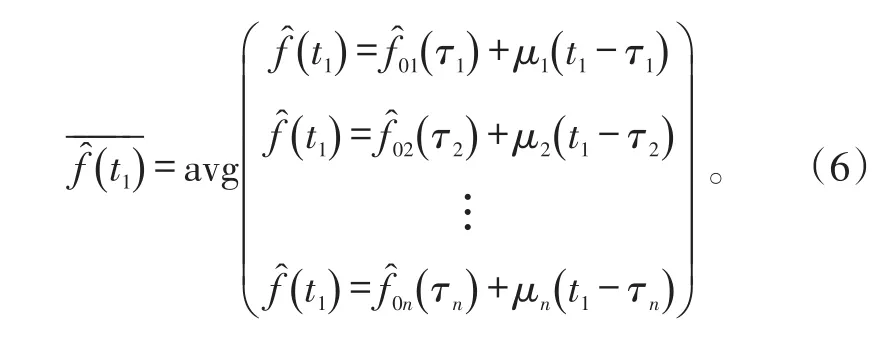
2.2 仿真

非线性调频信号各项参数与之前保持不变，仿真分别采用无重叠滑动、逐点滑动和逐点滑动取平均值3种方式进行，其中逐点滑动区分以第一采样时刻作为估计值和以中间采样时刻作为估计值2种情况，其瞬时频率估计精度如表1所示。

表1 不同滑动方式下的瞬时频率估计精度对比Tab.1 Comparison of instantaneous frequency estimation error using different moving-windows

从表1数据可以看出，采用第一采样时刻作为估计值的逐点滑动方式在众多滑动方式中对瞬时频率估计的精度最高，其次为采用中间时刻作为估计值的逐点滑动方式。无重叠滑动方式和逐点滑动取平均值的方式并不能取得预期的高瞬时频率估计精度，特别是逐点滑动取平均值的方式，在利用其对信号频率变化较剧烈的非线性调频信号进行瞬时频率估计时，可能反而会减弱瞬时频率估计精度，造成瞬时频率估计的误差。因此，并不适用于处理非线性调频信号。

3 结论

本文利用STFT作对比，首先从理论和仿真两方面分析了高斯噪声背景下的STFRFT时频分辨能力；然后，研究了STFRFT窗口滑动方式对瞬时频率估计的影响，可以发现：①STFRFT在抗噪声性能方面比STFT更为出色，尤其是在调频率较大或是变化剧烈时；②采用第一采样时刻作为估计值的逐点滑动方式在众多滑动方式中对瞬时频率估计的精度最高。因此，实际应用中，应主要采用该种滑动窗口方式。