我国一线城市房地产市场泡沫的测度研究<br/>——基于我国19个一线城市的面板数据

我国一线城市房地产市场泡沫的测度研究
——基于我国19个一线城市的面板数据

2019-08-07梁秋霞王馨平

滁州学院学报 2019年3期

梁秋霞，汪楠，王馨平

一、文献综述

从现有研究来看，我国学者在房地产泡沫的存在性及泡沫大小测度上不断探索并进行诸多尝试，取得显著成效的同时，也使我们有丰富成果可以借鉴。

当前学术界关于房地产泡沫的研究，存在两个方面：一是房地产泡沫的存在性检验；二是房地产泡沫大小的测度。主要方法有三类：第一类称为指标法，通过建立与房地产价格相关的单一指标或指标体系来反映房地产泡沫，该类方法包括简单指标法、功效系数法等。我国学者孙焱林、张攀红、王中林选取简单指标法、单位根—协整检验和市场供求法等七种方法，对上海市2003年-2011年房地产泡沫进行存在性检验和实证测度,并对七种方法进行了实证比较。[1]第二类称为统计检验法，其原理可以理解为如果房地产市场中不存在泡沫，则房价运行会表现出一定的统计规律，如果存在泡沫则统计规律不存在，该类方法常用的有方差上限检验、单位根-协整检验、设定性检验等。曾五一、李想通过房屋销售价格指数和租赁价格指数序列不同阶单整,并且二者不存在协整关系,证明在样本期间内我国35个大中城市房地产价格存在泡沫。[2]第三类称为理论价格法，也有学者称为模型法，通过建立数理模型计算房地产的理论价格，与房地产实际价格进行比较，二者的偏离程度即为房地产泡沫大小。根据建模思路的不同，该类方法可以分为收益还原法、边际收益法和市场供求法。郭熙保、吴金铎在文中定义房地产泡沫是指房地产价格偏离市场基础价格，因预期而使价格持续上涨的现象。并在此基础上建立随机效应模型，用31个省(市)1997-2009年的面板数据进行GLS回归检验我国房地产市场的泡沫程度，和各因素对泡沫的影响程度。[3]范新英、张所地、冯江茹借助A&H迭代模型求解均衡价格的基本思想，以我国35个大中城市1999-2011年的数据为研究对象，将由经济基本面决定的均衡价格与实际价格进行比较，从而测算出各个城市房价泡沫度。[4]这三类方法在实际中都有应用，也各有优劣。

但仍有值得改进的地方，一是在研究城市的选取上，大多数文献针对个别城市或全国大中城市进行研究，没有考虑城市之间的差异性；二是在使用面板模型对我国房价泡沫大小作定量判断时，鲜有严格的模型设定形式检验。本文基于上述不足，选取15个新一线城市，加上北京、上海、广州、深圳作为研究对象，建立面板模型进行泡沫测度实证研究。

二、指标数据的选取及理论模型

(一)指标和数据的选取

我国学者对房地产价格的各种影响因素进行了诸多理论分析及实证研究。赵赟飞研究结果表明人口流动推动房价上涨，两者存在高度近似的正相关关系。[5]宋连方、刘那那基于面板数据的中国房地产市场泡沫分析中对城镇居民可支配收入、银行信贷和土地交易价格对房地产市场的影响进行理论分析，并对房地产泡沫进行测度。[6]张超以长三角城市群作为研究对象，考虑到房地产泡沫受到供给和需求两个基本面的影响以及数据的可得性，文章选取收入、房地产开发投资额、金融机构5年期贷款利率等指标来测度房地产泡沫。[7]综上所述，考虑数据的可得性，本文变量选取Y为住宅商品房平均销售价格， IN为城镇居民可支配收入，XD为房地产开发贷款(国内贷款)，RK为年末总人口。所有变量以2005年为定基求出2006-2016年的增长率。

研究对象选取北京、上海、广州、深圳和2018年第一财经周刊评选的15个新一线城市共19个一线城市为横截面，以2005-2016年为时间跨度的面板数据进行实证研究，研究数据来源于国家统计局官网，历年的《中国房地产统计年鉴》和同花顺金融。所用软件为Eviews9.0。

(二)理论模型

从经济基本面来看，影响房价的因素来自供给和需求两个方面。在有效市场理论框架内，市场价格是对资产真实信息的反应，因而以可获信息为基础的房地产真实价格具有可测性。本文立足于经济基本面采用理论价格法建立如下影响房地产价格的理论模型：

Yit=αit+βitINit+βitXDit+βitXDit+εi

(1)

公式(1)中Yit为城市i在t时期的以2005年为定基的住宅商品房平均销售价格增长率，INit为城市i在t时期的以2005年为定基的城镇可支配收入增长率，XDit为城市i在t时期的以2005年为定基的房地产开发贷款(国内贷款)增长率，RKit为城市i在t时期的以2005年为定基的年末总人口增长率，εi为随机扰动项。

房地产泡沫度计算公式为：

城市i在时期t的房地产市场泡沫度

(2)

公式(2)中Yit*为城市i在时期t的内在价格增长率。(Yit-Yit*)即为面板回归方程求得的残差，是计算泡沫度的分子。

三、面板数据回归

(一)Panel Data模型概述

设有因变量yit与k×1维解释变量向量x′it=(x1,it，x2,it，…，xk,it)′，满足线性关系:

yit=αit+X′itβ′it+uit，i=1,2,…，N；

t=1,2，…，T

(3)

公式(3)为一般的线性面板数据模型。其中x′it=(x1,it，x2,it，…，xk,it)′为k维解释变量的向量形式，β′it=(β1,it，β2,it，…，βk,it)′为对应于解释变量向量x′it的k×1维系数向量，N为截面成员的个数，T为每个截面成员的观测时期总数，αit为模型的常数项，k为经济指标个数。随机扰动项uit之间相互独立，并且满足零均值、等方差。

(二)单位根检验

为了避免样本数据回归有较高的R2，但结果没有任何实际意义，即虚假回归的现象，保证面板模型回归结果的有效性，必须对面板数据的平稳性进行单位根检验。

对于面板数据，考虑如下的AR(1)过程：

yit=ρiyit-1+x′itδi+uit,i=1,2，…，N；t=1,2，…，Ti

(4)

公式(4)中：N表示N个截面成员，Ti表示第i个截面成员的T个观测时期，x′it代表外生变量。ρi是回归系数，假定随机扰动项uit之间符合独立同分布假设。如果∣ρi∣<1，则序列yi为平稳序列;如果∣ρi∣=1，则对应的序列yi包含一个单位根，即是非平稳的。

对参数ρi有两种不同的假定，一是假定其对于所有截面都是相同的，这种情况称为相同单位根过程下的检验，即假设公式(4)中的参数ρi满足ρi=ρ(i=1,2，…，N)。LLC检验(Levin，Lin，Chu检验)、Breitung检验和Hadri检验都是基于该种假设；二是假定其对于所有截面个体不同，该情况称为不相同单位根过程下的检验，即允许参数ρi跨截面变化。IPS检验(Im，Pesaran，Shin检验)、Fisher-ADF、Fisher-PP均是基于该假设。

本文选取相同单位根过程下的检验LLC(Levin-Lin-Chu)检验和不同单位根过程下的检验Fisher-ADF检验。前者零假设为各截面序列具有一个相同的单位根，后者零假设为各截面成员都有一个不相同的单位根。

所有变量的单位根检验都带有截距项，住宅商品房平均销售价格增长率Y和城镇可支配收入增长率IN除了截距项还有趋势项。变量滞后长度根据AIC准则，自动选择最大的滞后长度。

为避免繁琐，本文给出因变量Y的单位根检验。住宅商品房平均销售价格增长率Y折线图见图1。

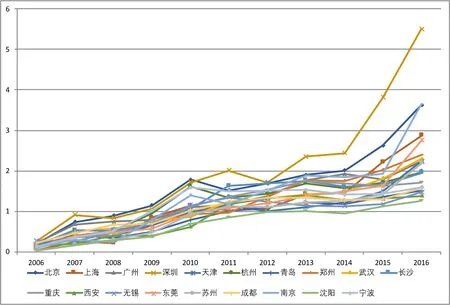
图1 住宅商品房平均销售价格增长率Y折线图

从图1可以看出住宅商品房平均销售价格增长率Y具有截距项和趋势项。住宅商品房平均销售价格增长率原始数据单位根检验见表1。

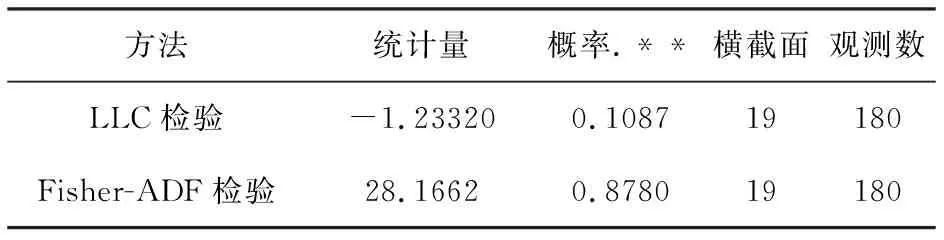
表1 住宅商品房平均销售价格增长率Y原始数据单位根检验

注：.**表示至少在10%的显著水平下显著。

从表1可以看出Y原始数据LLC检验和Fisher-ADF检验都认为有单位根，需要滞后一阶。住宅商品房平均销售价格增长率Y滞后一阶数据单位根检验见表2。

阿里偏着头，想了想，觉得阿东说得有理。于是他不等阿东开口教他怎么磕头，便使劲磕了起来。墓穴尚未封口，水泥边毛毛糙糙。等阿东制止他时，他的额头已经磕出了血，水泥边沾上他的血印。

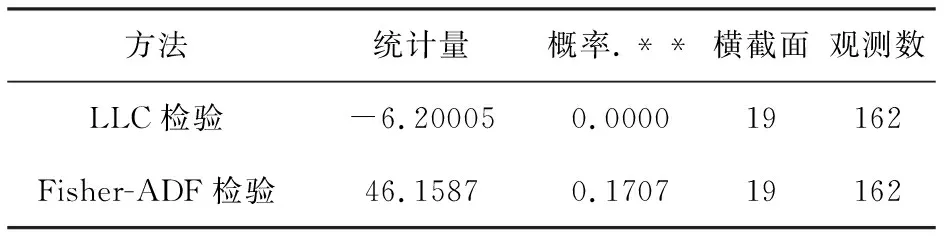
表2 住宅商品房平均销售价格增长率Y滞后一阶数据单位根检验

注：.**表示至少在10%的显著水平下显著。

表2得出Fisher-ADF检验仍认为有单位根，需要进一步检验。住宅商品房平均销售价格增长率Y滞后二阶数据单位根检验见表3。

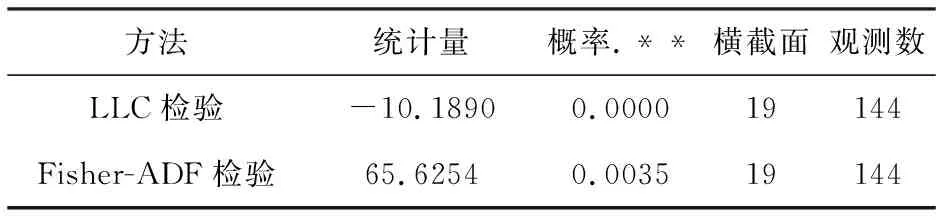
表3 住宅商品房平均销售价格增长率Y滞后二阶数据单位根检验

注：.**表示至少在10%的显著水平下显著。

从表3可以看出滞后二阶后，LLC检验和Fisher-ADF检验都认为其没有单位根，住宅商品房平均销售价格增长率Y滞后二阶数据平稳。按照类似的方法，IN、RK均为滞后二阶平稳。XD单位根检验为一阶平稳，对XD滞后一阶进行单位根检验，结果显示XD(-1)为一阶平稳。即住宅商品房平均销售价格增长率Y、城镇人均可支配收入增长率IN 、房地产开发贷款(国内贷款)增长率XD，年末总人口增长率RK均为I(2)变量。

(三)协整检验

通过协整检验，可以判断变量之间是否存在长期稳定的均衡关系。若存在，此时方程回归残差是平稳的，可以在此基础上对原方程进行回归，回归结果是较精确的。

协整检验的前提是在单位根检验的基础上进行，只有变量之间是同阶单整，才可以进行协整检验。

Eviews中面板数据的协整检验方法有Pedroni检验、Kao和Fisher面板协整检验。本文采用Kao检验。

住宅商品房平均销售价格增长率Y，城镇可支配收入增长率IN，房地产开发贷款(国内贷款)增长率XD，年末总人口增长率RK用Kao检验协整检验结果见表4。

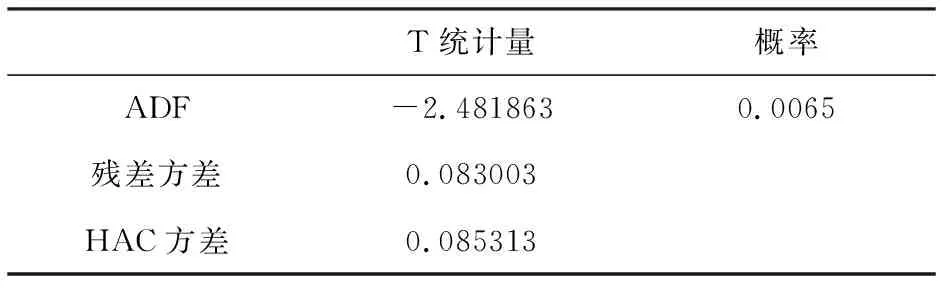
表4 Kao协整检验结果

表4结果显示住宅商品房平均销售价格增长率Y，城镇可支配收入增长率IN，房地产开发贷款(国内贷款)增长率XD，年末总人口增长率RK存在协整关系。

(四)Panel Data 模型的检验与回归

在对Panel Data模型进行回归时，样本数据中存在截面、时期和变量3个维度上的信息。模型形式的设定影响着估计结果与所模拟的经济现实的偏差。所以在对面板数据模型进行回归时需要对模型的设定形式进行检验，检验是混合回归模型、变截距模型还是变系数模型，还要检验模型的固定效应和随机效应，从而避免模型设定的偏差，改进参数估计的有效性。

1.固定效应还是随机效应。Hausman检验的用途很广。比如模型丢失变量的检验、变量内生性检验、模型嵌套检验、建模顺序检验可以通过H检验来做。通过Hausman检验还可以确定模型形式的检验。

原假设与备择假设是：

H0:个体效应αi与解释变量Xit无关(个体随机效应模型)

H1:个体效应αi与解释变量Xit相关(个体固定效应模型)

个体随机效应模型下H检验结果见表5。

表5 个体随机效应模型Hausman检验

从表5可以看出Hausman检验的值对应的概率小于5%，因此拒绝个体变量与回归无关的假设，建立个体固定效应模型。

2.变系数还是变截距。假设1：解释变量的斜率在不同个体或时期上相同，但截距不同。则该模型形式为变截距模型：

H1:Yit=αit+β1IN1it+β2XD2it+β3RK3it+uit

(5)

检验结果接受了假设1即为变截距模型，拒绝假设1则为变斜率模型，即采用变系数模型：

H2:Yit=α+β1iIN1it+β2iXD2it+β3iRK3it+uit

(6)

检验假设1的F统计量为：

其中，模型中α为常数，β为系数，检验公式中，S1、S2分别为采用公式(6)、(5)时估计的残差平方和，n为截面个数，T为时期数，K为非常数项解释变量个数。得到F1=3.223349111，在Eviews中求出F0.05(72,114)=1.410634705。即：

F1>F0.05(72,114)，拒绝假设1，采用变系数模型。

3.回归结果。在固定效应变系数模型下回归效果显著性结果见表6。

表6 固定效应变系数回归结果

从表6得出R2=0.93,DW=1.65,回归效果比较显著。

四、泡沫度测算及分析

在Eviews 9.0中生成回归残差，利用残差求得泡沫度值见表7。

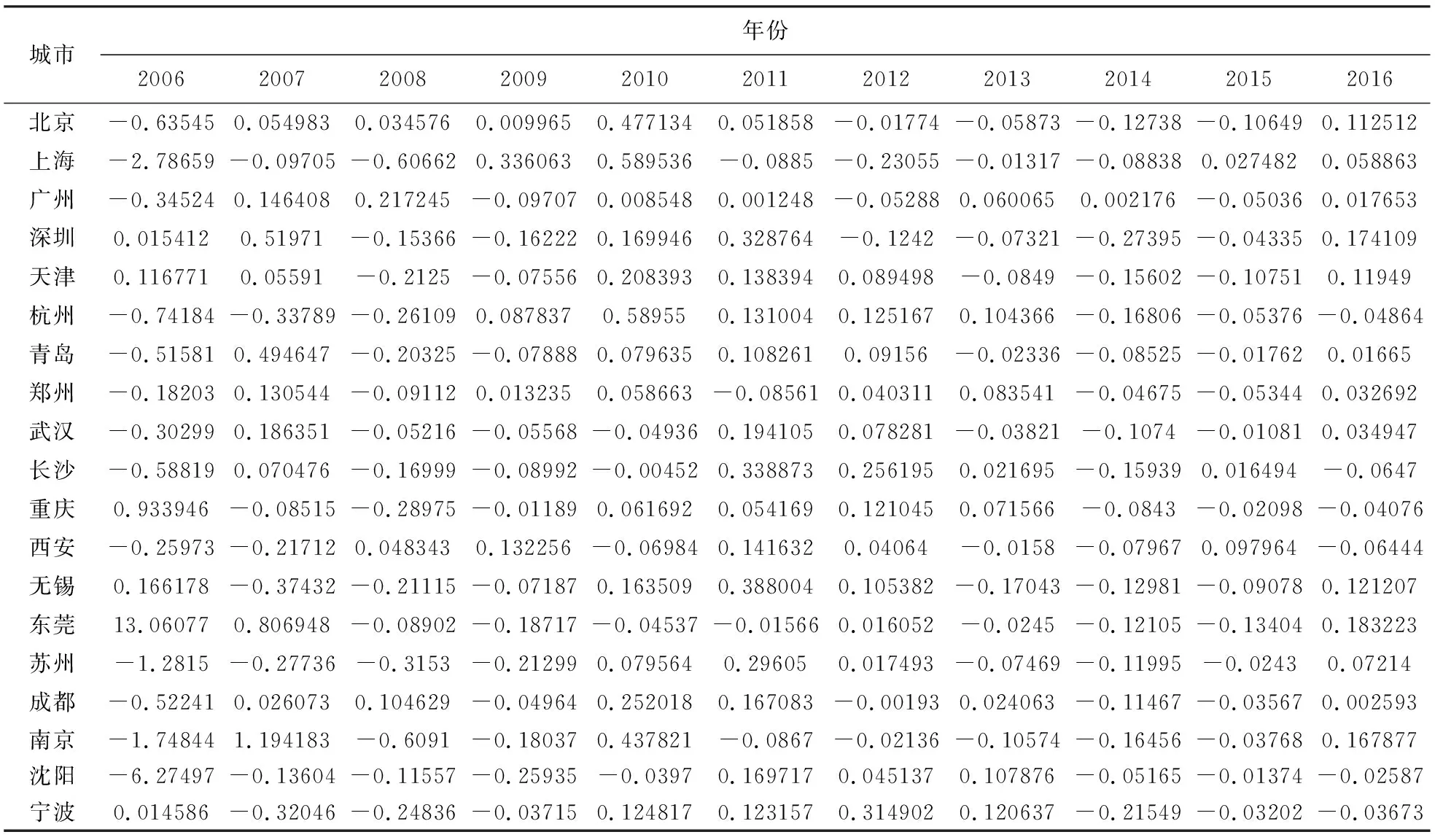
表7 泡沫度值

北京上海广州深圳和2018年第一财经周刊评选的15个新一线城市泡沫度折线图见图2。

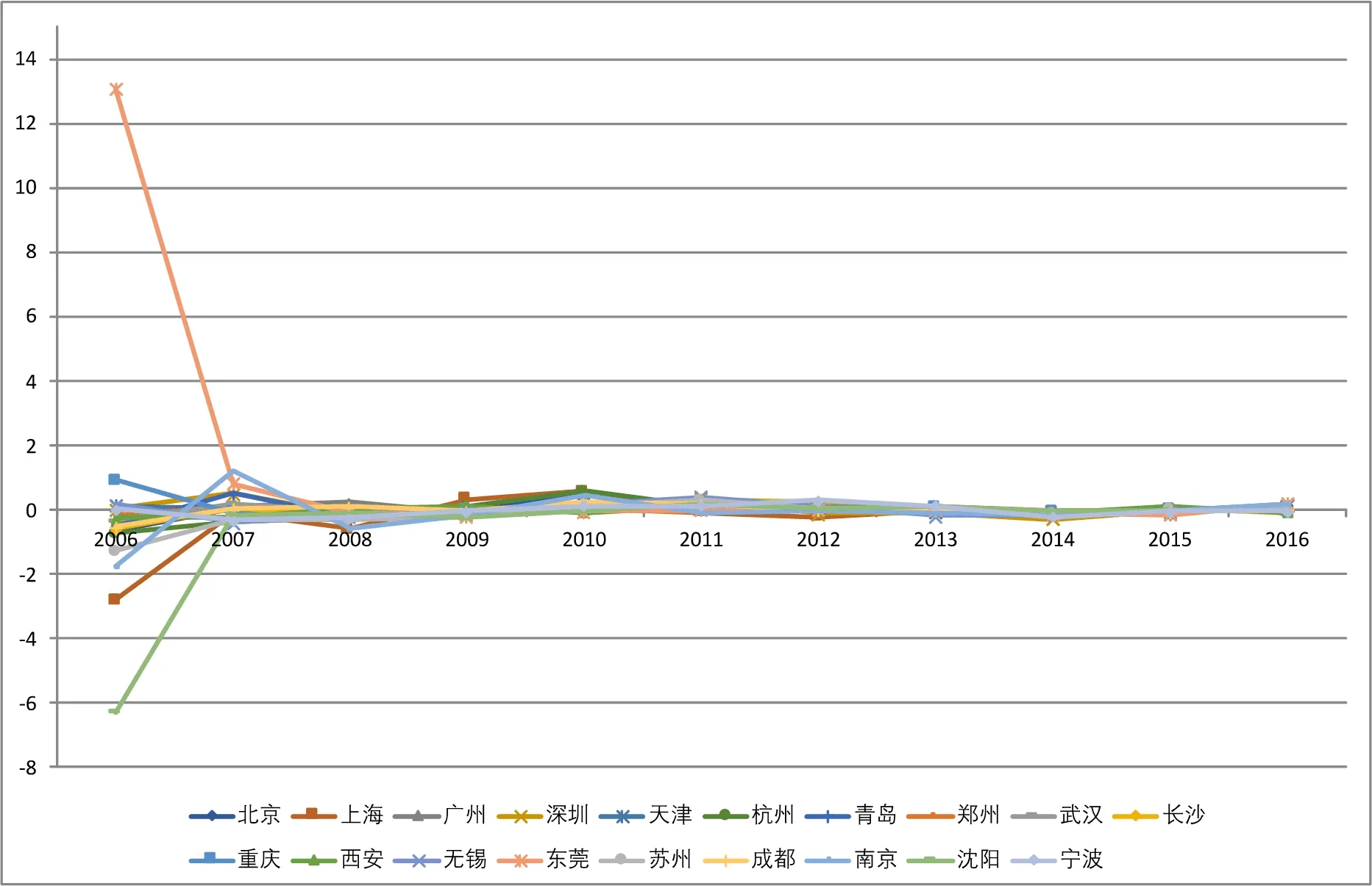
图2 十九个城市泡沫度折线图

从上表可以看出总体房地产泡沫最大的年份是2006年，其次是2007年和2008年，最后是2010年。总体泡沫十分明显的2006中年泡沫度最大的是重庆和东莞，而不是北京和上海。北京房地产泡沫度最大的年份是2010年，上海泡沫度最大的年份是2009年和2010年。

五、对策建议

(一)建立控制房价上涨的长效机制

从实证结果来看，一线城市泡沫度整体呈下降趋势。我国针对房地产市场宏观调控政策的不断出台，对房地产市场起到一定降温作用。但政府对房地产市场的宏观调控政策本身根据市场相机抉择，虽对房地产泡沫抑制作用明显，但从长远来看，房地产泡沫得不到长效的解决。由于房地产业牵引诸多行业，对消费者居住买房造成困扰的同时，也不利于国民经济的稳定发展。政府应建立起可持续稳定发展的中国住房租赁市场，商品住房销售和住房租赁市场并举发展的市场。同时合理引导一部分房地产投资需求，如推出一些房地产性质的投资产品等。