基于构件模态失谐模型的涂层整体叶盘失谐辨识

徐昆鹏， 孙 伟， 高俊男， 梅雪峰

(1. 东北大学 机械工程与自动化学院，沈阳 110819； 2. 东北大学 航空动力装备振动及控制教育部重点实验室，沈阳 110819； 3. 辽宁轨道交通学院，沈阳 110027)

整体叶盘作为航空发动机的重要核心部件之一，是提高发动机性能、简化结构、降低重量、提高耐久性与可靠性的重要结构，其品质优劣直接决定了航空发动机的寿命与性能。由于缺少榫头-榫槽的摩擦阻尼减振环节，整体叶盘在气动、机械、温度场等载荷的共同作用下很容易产生共振而使叶盘结构发生疲劳失效。因而抑制整体叶盘过大的振动、减少疲劳损伤等已成为整体叶盘设计研发过程中必须解决的一个关键环节。

目前，面向整体叶盘减振的方法通常有以下几类：在轮盘或叶根处增加阻尼结构[1]、叶片涂层[2]及摩擦阻尼器[3]等。其中叶盘涂层减振是在整体叶盘叶片部位涂敷涂层材料以增加系统的阻尼能力，以达到减振的目的。可用的涂层材料主要有黏弹性有机高分子类材料和硬涂层阻尼材料两类[4]，而由金属基、陶瓷基或两者的混合制成的硬涂层材料具有足够的强度、韧性的同时，具有在高温、高腐蚀环境下保持较高阻尼能力的特点[5-6]，因而这里研究整体叶盘硬涂层阻尼减振。硬涂层减振是一种新兴的被动阻尼减振技术，其主要利用涂层颗粒的内摩擦产生阻尼耗能。目前，研究者以针对硬涂层阻尼材料制备[7]、材料参数辨识[8]、复合结构建模[9-10]等开展了大量研究，这些都可作为本文整体叶盘硬涂层减振研究的基础。

理论上，整体叶盘应为周期对称结构，但由于制造误差、材质不均、使用磨损及人为设计等因素，实际每个扇区间会存在小量差别，这些小量差别称之为失谐[11]。涂敷涂层后整体叶盘更有可能存在失谐现象，因此，需要开展涂层后整体叶盘失谐辨识研究，对加装涂层的整体叶盘失谐程度进行科学地判定，这对于整体叶盘涂层减振设计具有重要意义。

关于整体叶盘的失谐辨识，学者们已做了大量研究。Feiner等[12-13]基于FMM(Fundamental Model of Mistuning)减缩模型提出以系统响应进行失谐辨识的方法，该方法只适用于孤立模态族，可以对叶盘的叶片和扇区进行失谐辨识，并通过试验进行了验证。Lim[14]对CMM(Component Mode Mistuning)减缩建模的辨识方法进行了发展，使得不需要外力数据，只需要实测的强迫响应数据，甚至只有固有频率和振型为初始数据，就可以进行失谐辨识。Nyssen等[15-16]基于CMM减缩建模提出了实验分析方法来辨识整体叶盘的失谐，并通过对单级和多级叶盘进行实验研究分析，验证了方法的有效性。王帅等[17-18]基于公称模态子集(Subset of Nominal Modes,SNM)降阶技术，以谐调叶盘有限元模型解析模态和真实失谐结构的稳态响应作为基础信息，提出一种整体叶盘结构失谐辨识方法。

总览以上辨识方法和辨识对象，涉及的整体叶盘材质均为单一材料，而涂层整体叶盘是由两种材料组成的复合结构。因此，原有的整体叶盘建模及失谐辨识方法均需要重新修正。目前，针对涂层整体叶盘建模研究已经初步开展[19-20]，但还没有涂层整体叶盘失谐辨识的研究。

本文基于构件模态失谐建模方法，提出一种面向涂层整体叶盘涂层的失谐辨识办法。进行了基础理论和辨识公式的推导，给出了辨识流程，并以一个简化涂层整体叶盘为例进行了失谐辨识研究。进一步，基于辨识结果构建了失谐整体叶盘新的分析模型，通过对比新模型与原模型获得的涂层整体叶盘固有特性，证明了本文方法的合理性。

1 构件模态失谐模型概述

构件模态失谐建模方法采用了一种特殊的子结构分解原理见图1，将失谐整体叶盘的谐调部分作为一个子结构，称为谐调子结构见图1(b)；将失谐结构和谐调结构之差所确定的质量矩阵和刚度矩阵来确定的部分作为另一个子结构，称为失谐子结构。图1(c)仅为叶片失谐时的情况。

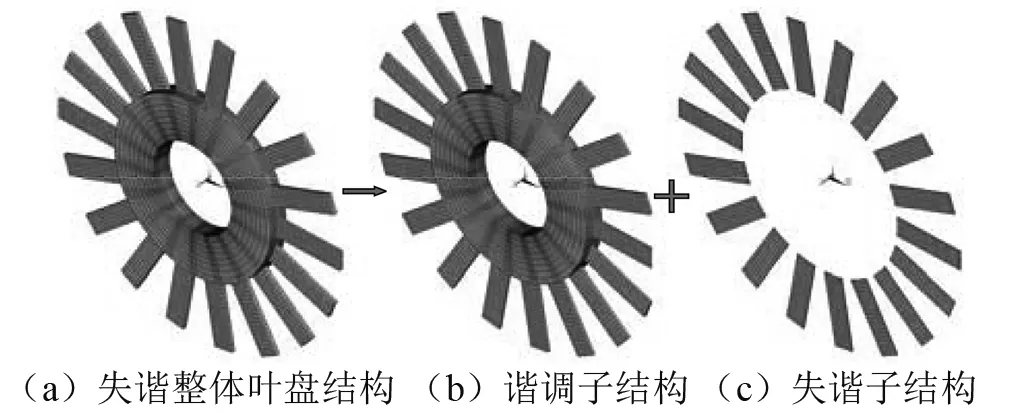
图1 失谐整体叶盘分解方式Fig.1 Decomposition of mistuned blisk

由于整体叶盘的响应对叶片失谐的灵敏度比对轮盘的要大得多，因而大多涂层减振主要是针对叶片，叶片涂层整体叶盘结构见图2。在未涂敷涂层时，叶盘基体由于制造、使用磨损等因素导致的各扇区之间存在的微小失谐量远小于涂层产生的失谐量，因此，对于涂层整体叶盘可以将涂层前的结构视为谐调结构，将涂层结构部分作为失谐结构进行研究。这种分解方法与CMM法分解原理较吻合，因此，通过该方式辨识的失谐量是涂层部分相对于未涂层叶盘所产生的失谐。

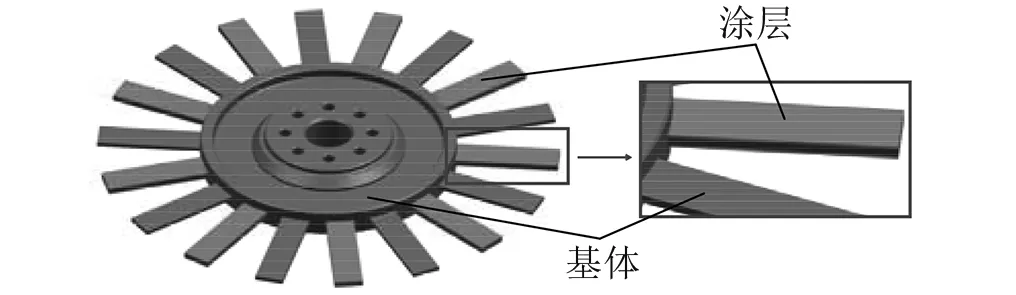
图2 涂层整体叶盘结构Fig.2 Structure of coating blisk

2 失谐辨识理论推导

考虑涂层失谐的整体叶盘的频域自由振动方程可表达为

-ω2(M0+ΔM)X+(K0+ΔK)X=0

(1)

式中：X为涂层整体叶盘自由振动响应向量；ω为涂层整体叶盘自由振动圆频率；M0，K0分别为无涂层整体叶盘(谐调叶盘，即叶盘基体)的质量和刚度矩阵； ΔM，ΔK分别为涂层整体叶盘失谐结构(即涂层部分)的质量和刚度矩阵。

令

X=ΦP

(2)

式中：Φ为无涂层整体叶盘(谐调叶盘)的正则振型矩阵；P为正则坐标向量。

将式(2)代入式(1)，并对公式等号左右两侧同时左乘ΦT可得到

-ω2(ΦTM0Φ+ΦTΔMΦ)P+
(ΦTK0Φ+ΦTΔKΦ)P=0

(3)

式中：ΦTM0Φ=I(I为单位矩阵)；ΦTK0Φ=Λ0， 其中Λ0为无涂层整体叶盘(谐调叶盘)的正则刚度矩阵，因此式(3)可变换为

-ω2(I+ΦTΔMΦ)P+(Λ0+ΦTΔKΦ)P=0

(4)

式中：ΦTΔMΦ与ΦTΔKΦ分别为涂层整体叶盘的模态失谐质量和刚度矩阵。

对于涂层整体叶盘，可认为叶片间的质量失谐是由于在叶片上涂敷涂层材料的质量差异引起的(忽略基体微小质量失谐)。由于涂层的质量与涂层的几何尺寸(对于叶片全涂敷情况)成正比，可定义质量差异系数矩阵hj(整体叶盘未加涂层时的叶片质量和该叶片上涂敷涂层材料时的质量比)来近似描述涂层整体叶盘叶片间的质量失谐程度。质量差异系数矩阵hj的求解式为

hj=ΔMj(MCB)-1=diag(hj)

(5)

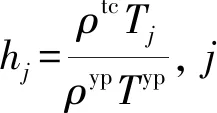
根据构件模态失谐模型，进一步对式(4)中模态失谐刚度矩阵ΦTΔKΦ进行减缩处理得到

(6)

式中： ΔKj为涂层整体叶盘第j个叶片的失谐刚度矩阵；Φj为无涂层整体叶盘(谐调叶盘)第j个叶片的振型矩阵。

令

(7)

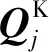
(8)

式中：ΛCB为理想悬臂叶片固有圆频率平方的对角矩阵；KCB为理想悬臂叶片刚度矩阵。将式(7)代入式(6)得到

(9)

式中： (ΦCB)TΔKjΦCB为每个叶片的模态失谐刚度矩阵。由于仅有对角项在减缩矩阵中起主导作用，失谐引起的悬臂叶片模态间耦合的非对角元素可以忽略，因此，(ΦCB)TΔKjΦCB可以进一步简化为

(ΦCB)TΔKjΦCB≈diagr∈R(kj.r)

(10)

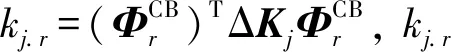
将式(10)代入式(9)得到

(11)

类似的，对式(4)中的模态失谐质量矩阵ΦTΔMΦ进行减缩处理得到

(12)

令

(13)

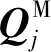
(14)

将式(13)代入式(12)得到

(15)

由式(5)可得

ΔMj=hjMCB

(16)

将式(16)代入式(15)得到

(17)

将式(11)和式(17)代入式(4)得到

(18)

令

(19)

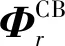
向量k即为需要辨识的刚度失谐参数向量，其反应的是失谐对涂层整体叶盘的叶片相对于理想悬臂叶片在频率上的影响。在实际进行刚度失谐参数辨识时，需要将式(18)具体化为

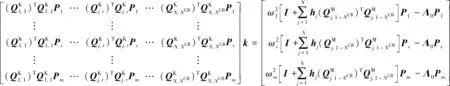
(20)

可见，通过式(5)和式(20)就可实现对涂层整体叶盘质量和刚度失谐的辨识。

3 失谐辨识流程

按照第2部分推导的辨识原理，涂层整体叶盘失谐的辨识可参照以下4步进行，这里有限元分析部分使用的软件为ANSYS。

(2) 质量失谐辨识计算

根据叶片涂层方案获得涂层材料密度ρtc和每个叶片涂层厚度Tj， 以及基体材料密度ρyp和叶片基体厚度Typ， 按照式(5)计算质量差异系数hj(质量失谐参数)。

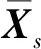
(21)

(4) 刚度失谐辨识计算

将以上三步计算结果代入式(20)进行刚度失谐辨识计算，得到刚度失谐参数k。

4 实例研究

4.1 问题描述

这里，以具有18个叶片的硬涂层整体叶盘作为研究对象来实践本文研发的失谐辨识方法。涂层整体叶盘的有限元模型及各叶片编号见图3，其中，未涂层的叶片厚度为3 mm，在偶数叶片上下双面涂敷不同厚度涂层以构造由涂层引起的失谐，具体涂层厚度见表1。在该有限元模型中，叶盘基体及涂层部分均采用SOLIDE54实体单元，整个模型中共有32 400个单元，81 184个节点。叶盘基体材料为45钢，涂层材料为NiCoCrAlY+YSZ，这两种材料的相关参数见表2。

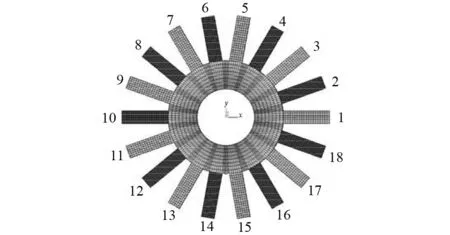
图3 涂层整体叶盘有限元模型Fig.3 Finite element model of coating blisk

叶片编号2/4/148/12/166/10/18奇数单面涂层厚度/mm0.10.20.30

表2 涂层整体叶盘材料参数

4.2 失谐辨识

按照推导的辨识算法及提出的辨识流程对图3所示的涂层整体叶盘进行失谐辨识。

图4 理想悬臂叶片有限元模型Fig.4 Finite element model of nominal cantilever blade

图5 整体叶盘谐调部分有限元模型Fig.5 Finite element model for tuned part of coating blisk

根据表1数据及式(5)计算质量差异系数hj(即质量失谐)，计算结果见图6。

图6 质量差异系数Fig.6 Mass discrepancy coefficient

图7 涂层整体叶盘有限元模型Fig.7 Finite element model of coating blisk

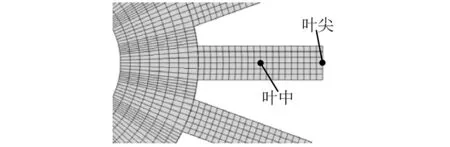
图8 叶片上取样点位置Fig.8 The positions of the sampling points on the blades

最后，通过式(20)求解刚度失谐参数k，计算结果见表3。进一步，通过刚度失谐参数k得到涂层整体叶盘叶片频率失谐率，图9给出了叶片频率失谐率与叶片涂层厚度的对比。可以看出叶片频率失谐率的趋势与涂层厚度变化基本一致，这客观上也说明了辨识结果的正确性。综上，就实现了对由涂层引起的失谐整体叶盘质量及刚度失效的辨识。

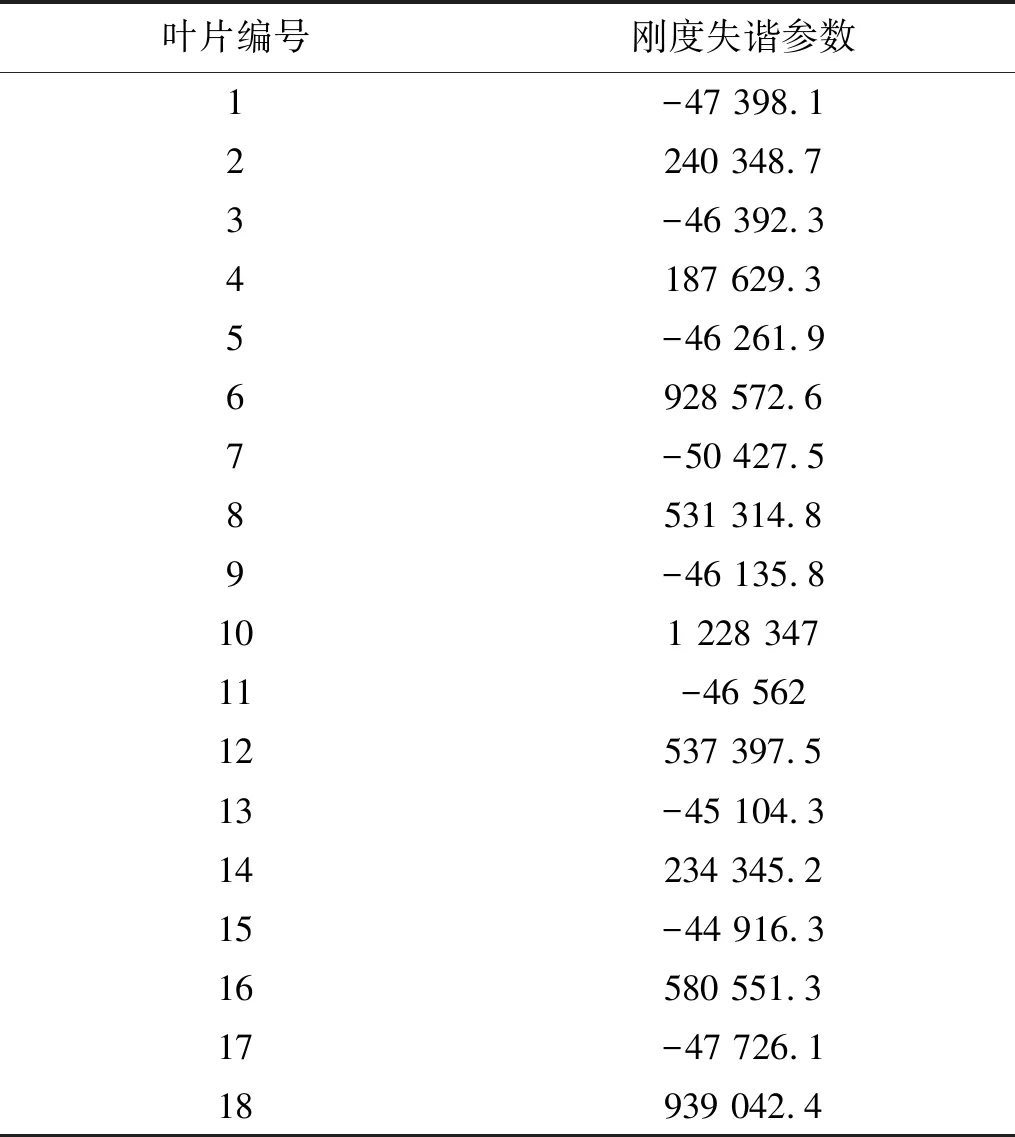
表3 刚度失谐参数k计算结果

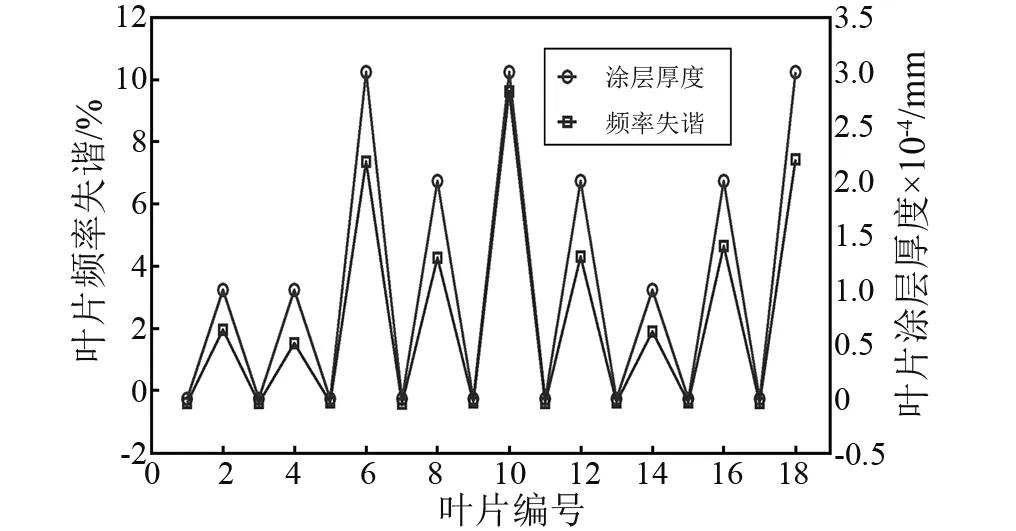
图9 叶片频率失谐率与涂层厚度变化趋势对比Fig.9 Comparison between the frequency mistuning rate of the blades and the thicknesses of coatings

4.3 辨识结果正确性校验

为了校验辨识结果的正确性，这里建立了一个新的失谐整体叶盘简化有限元模型。此模型是在无涂层整体叶盘结构的基础上，根据辨识得到的质量失谐参数hj和刚度失谐参数k对每个叶片的密度和弹性模量进行修正得到的，通过对比新建失谐整体叶盘模型(简称“新失谐模型”)与原涂层整体叶盘有限元模型(简称“原失谐模型”)的固有特性(即固有频率和对应点振型)是否一致，来验证辨识结果的正确性。具体验证过程与结果分析如下：

4.3.1 固有频率对比

分别提取由新失谐模型与原失谐模型获得的涂层整体叶盘前35阶固有频率，并计算频率偏差，相关结果见图10。由图10可知，两个模型的固有频率基本一致，最大偏差为-1.55%(第16阶)，最小偏差为接近0(第4阶)，频率偏差在-1.55%～1.01%。

图10 第1～35阶频率对比Fig.10 1—35 order frequency

4.3.2 模态振型对比

按照图8所示的两个点，分别提取新失谐模型与原失谐模型前35阶振型，并利用模态置信因子(Modal Assurance Criterion,MAC)比较获得的各阶振型的一致性。从获得的结果(见图11)可知，由两种模型获得的绝大多数阶次的振型向量相似度较高。

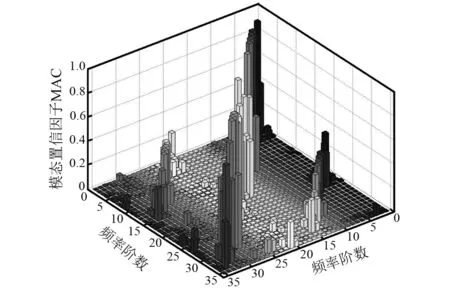
图11 第1～35阶模态置信因子值Fig.11 Modal assurance criterion of 1—35 order

可见，由两种模型获得的固有频率及振型均有很好的一致性，因而可以证明所辨识出的刚度及质量失谐是正确的。

5 结 论

涂层整体叶盘的失谐辨识是整体叶盘涂层减振研究的基础。本文基于构件模态失谐模型提出了一种适用于涂层整体叶盘失谐辨识的方法，得到以下结论：

(1) 涂层整体叶盘的复合结构包含谐调的叶盘基体以及涂层引起的失谐，这与构件模态失谐模型分解原理基本一致，因而可用CMM模型对涂层整体叶盘进行失谐辨识。

(2) 在推导涂层整体叶盘失谐辨识原理时，根据涂层叶盘的结构特点，将质量失谐辨识进行了近似处理，使得刚度失谐辨识结果能够兼顾到质量失谐的因素。实践表明这种处理方式可显著提高辨识效率，并使辨识结果更加全面。

(3) 基于所推导的辨识原理，提出了面向涂层整体叶盘失谐辨识的基本流程，包括质量及刚度失谐模态参因子计算、质量失谐辨识、求解正则坐标向量和刚度失谐辨识等4个步骤。该流程需要输入参数较少且容易获取，因而使涂层整体叶盘失谐辨识简便且易行。

(4) 以一个简化的涂层整体叶盘为例，实践了所研发的失谐辨识方法及流程。结果表明辨识结果与预设的涂层厚度变化基本一致。另外，还由辨识得到的质量失谐参数hj和刚度失谐参数k构建了一个新的失谐整体叶盘分析模型，通过对比由新模型与原模型获得的固有频率及振型，发现两者基本一致，从而进一步证明了辨识结果的合理性。