双馈感应风力发电机组鲁棒自适应协同镇定控制研究

吴忠强， 李 峰， 杜春奇, 张 伟

(燕山大学 电气工程学院 工业计算机控制工程河北省重点实验室, 河北 秦皇岛 066004)

能源是人类生存和发展重要的物质基础，随着人类社会的发展进步，能源对于人类经济社会发展的制约和对环境的影响越来越大[1]。常规能源，如煤、石油、天然气等资源有限，并且存在严重的污染问题。因此，对可再生能源的开发具有重大的研究意义，尤其是风能的开发利用在近些年来备受关注。面对风能的大规模开发利用，对于风力发电机组的控制问题也显得尤为重要。近几年，风力发电及其控制技术得到了快速的发展，并取得了丰硕的成果[2-4]。

发电机组是风力发电系统中重要的装置，它将风能转化为电能，直接影响输出电能的质量和效率[5-9]。因此，发电机组的控制技术是风电机组以及风力发电系统推广的关键。面对风力资源的大规模开发利用，对于风力发电机组的控制问题，专家和学者们进行了大量的研究探索，其中既有传统的线性控制方法，也有新的非线性领域的研究成果。文献[10]利用微分几何理论中的坐标变换对双馈感应发电机的三阶模型进行了精确的线性化。将线性模型转化为Bronovsky标准形。然后将线性二次型调节器的设计方法引入，得到了此线性系统的最优控制器。该控制方法可以提高电力系统的暂态稳定性，提高系统的阻尼。但控制的鲁棒性不高，适用范围略窄。文献[11]利用模糊控制技术提出了一种不依赖交流励磁发电机精确数学模型的励磁控制方案，建立了交流励磁发电机全模糊解耦控制模型，并对其进行了分析。该控制器动态性能优良，但需要在控制过程中精确测量定子电压、电流，转子位置角及转速，实现比较繁琐。文献[12]提出了发电机侧变流器的最大功率提取控制策略。当偏远地区的电力网络连接不可行时，利用本地资源，使用当地小型独立式分布发电系统控制一个独立模式的负载，使得输出电压的振幅和频率等控制在可处理可变换的状态，控制器可提取最大功率，并在不同的风和负载条件下实现电压和频率的调节。文献[13]提出基于径向基函数神经网络的发电机模型，对发电机组进行数据训练并且测试径向基函数网络，探讨了径向基函数宽度、神经元数对径向基函数收敛精度的影响。该方案有自适应控制的优点，但并没有对实时性做出讨论分析。文献[14]将自抗扰控制技术和BP神经网络相结合，应用到双馈风力发电机并网运行控制中，提出了一种新的双馈风力发电机并网运行控制方案。该方案具有优良的动态性能，对内外扰动也具有较强的鲁棒性，但该控制策略略显复杂。

Hamilton系统来源于经典力学中的一类保守非线性系统，是非线性科学研究中的重要领域之一，刻画了大部分保守物理系统的动态行为。然而，随着人们不断的探索使用，发现经典的Hamilton系统具有很大的局限性，于是对其不断地进行扩展，形成了当前的广义Hamilton系统。广义Hamilton系统在风电机组等非线性控制领域的研究正在蓬勃发展[15-18]。 高勇等从能量的角度对单台双馈电机的无源控制方法进行了研究，所设计出的控制器对参数摄动和负载转矩变化具有较强的鲁棒性，但是没有考虑外界扰动的影响。王冰等针对海上风力发电机群，基于Hamilton函数给出了一种分布式的控制策略，但该研究未考虑系统中结构参数的不确定性，具有一定的局限性。本文运用预反馈控制将双馈感应电机非线性系统转换为端口受控的耗散Hamilton系统，针对系统含有外部干扰和结构参数不确定的情况，设计一种输出反馈+自适应干扰抑制的多机同步控制器，使风电机组能够实现协同镇定，并有较强的鲁棒性和自适应性。

1 双馈感应发电机模型及其Hamilton模型建立

典型的双馈感应风力发电机组由变速箱和双馈感应发电机组成，变速箱可以表示为一阶模型，双馈感应发电机忽略定子的电磁瞬态时，可表示为二阶模型，则采用的第i台双馈感应发电机三阶模型如下

(1)

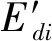
选取系统的Hamilton函数为

(2)

采用如下控制律

ui0=Ki+ui

(3)

式中：Ki为预控制器[19]；ui为控制分量。

(4)

式(1)可表示为

(5)

其中，

输出函数设计为

(6)

2 双馈感应发电机组的鲁棒自适应协同镇定

考虑双馈感应发电机模型式(1)中的定转子自感，互感，转动惯量和定子电流的不确定性，以及风速的波动性，将双馈感应发电机模型表示成既有外部干扰又有结构参数不确定的形式

(7)

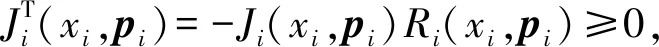
现需设计一种自适应L2干扰抑制控制器，使得在该控制器的作用下满足：当w=0时，由式(10)给出的N个双馈感应发电机同时渐近稳定。相应闭环系统的L2增益(从w～z)不大于给定的γ>0[20-21]。

假设(i1,i2,...,iN)是{1,2,…,N}的一个N级排列，L是一整数且满足1≤L≤N-1。

将上述N个双馈感应发电机分为两组：{∑i1, ..., ∑iL}和{∑iL+1,...,∑iN}，则有

(8)

(9)

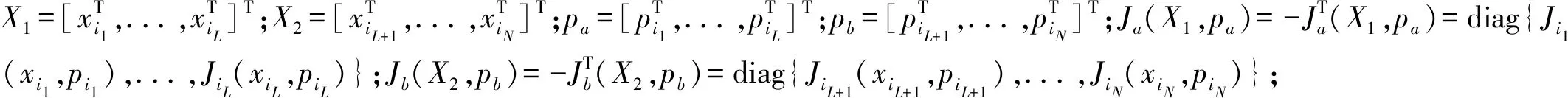
为了设计控制器，给出以下假设：

假设1 存在一个对称矩阵Q、一个N级排列(i1,i2,...,iN)和一个正整数L(1≤L≤N-1)，使得

(10)

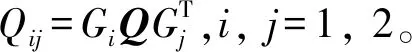
假设2 存在矩阵ψ，使得

[Ji(xi,pi)-Ri(xi,pi)]ΔHi(xi,pi)=giψθ

(11)

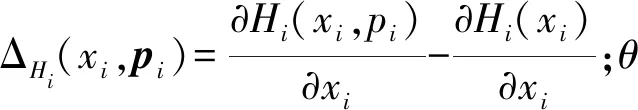
假设3di=gi，i=1,2,...,N。

在以上三个假设均成立的情况下，设计如下输出反馈+自适应L2干扰抑制控制器

(12)

下面证明控制器能使系统自适应镇定且满足L2干扰抑制性能。

u2可改写成

(13)

根据假设1和假设2易知式(8)与式(9)可由u1反馈扩展为式(14)

(14)

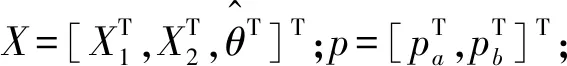
取

罚信号可写为

(15)

假设4 给定干扰抑制水平γ，式(16)成立

(16)

根据假设1和假设3可得出

(17)

将控制器式(13)代入式(14)，可计算得到

(18)

所以

(19)

又根据假设4有

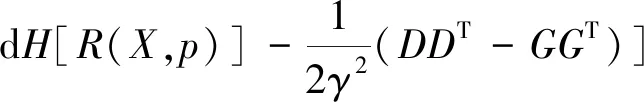
(20)

由式(19)得下列耗散不等式

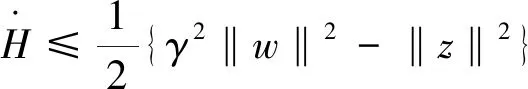
(21)

沿着由式(14)和式(12)组成的闭环系统轨线成立。

3 仿真研究

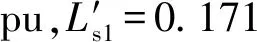
给出两DFIG协同控制系统结构图如图1所示。

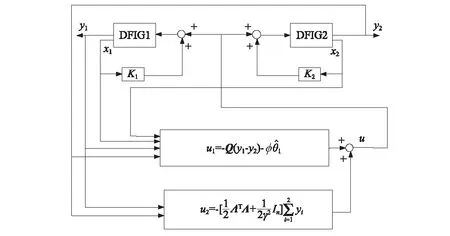
图1 DFIG 控制系统结构图Fig.1 DFIG control system structure diagram

仿真中考虑常值风速的情况，利于比较控制器的控制效果，取两风力机捕获的风能为：Pm1=Pm2=1.5 pu，仿真结果如图2～图7所示。

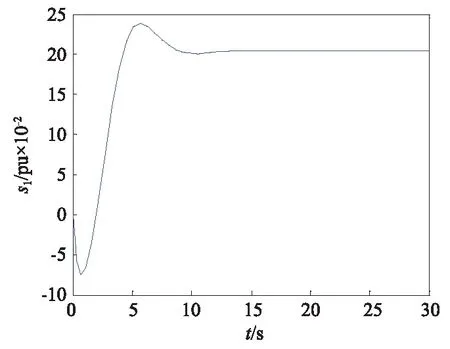
图2 1号发电机转子滑差s1的响应曲线Fig.2 The rotor slip response curveof the first generator

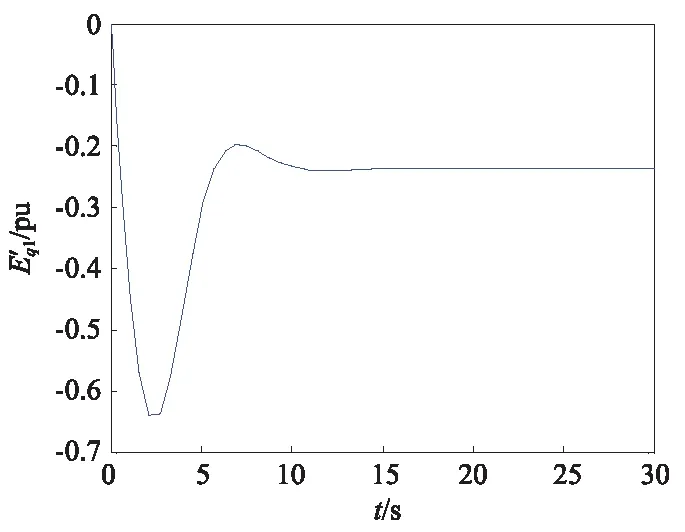
图3 1号发电机q轴电压的响应曲线Fig.3 The transient potential response curve of the first generator in q-axis

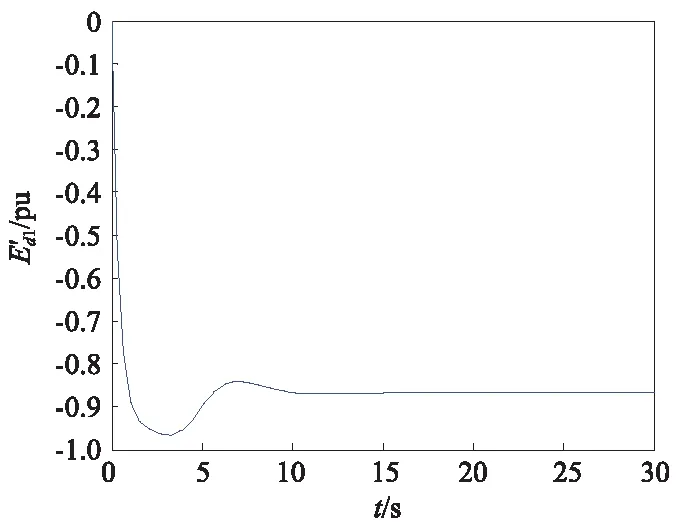
图4 1号发电机d轴电压的响应曲线Fig.4 The transient potential response curve of the first generator in d-axis

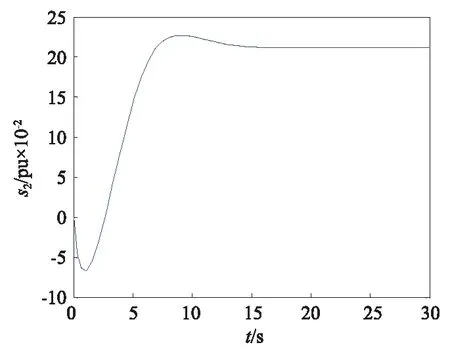
图5 2号发电机转子滑差s2的响应曲线Fig.5 The rotor slip response curve of the second generator

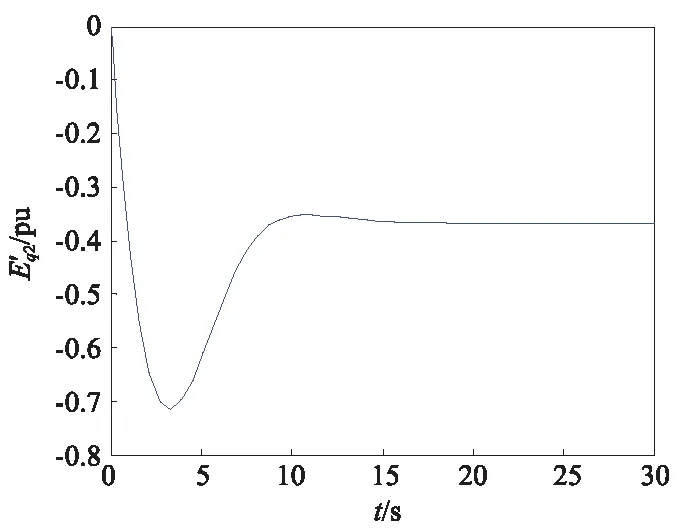
图6 2号发电机q轴电压的响应曲线Fig.6 The transient potential response curve of the second generator in q-axis

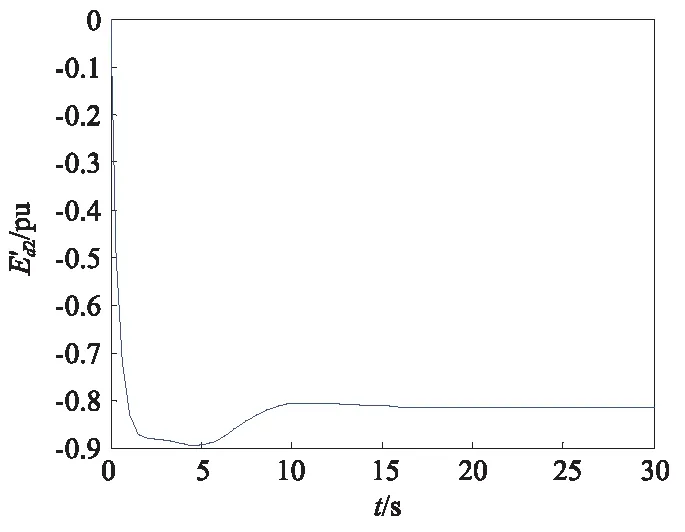
图7 2号发电机d轴电压的响应曲线Fig.7 The transient potential response curve of the second generator in d-axis

由图2～图7可看出所设计的控制器可使各个发电机的转子滑差稳定在理想的数值上，各个发电机的q轴电压和d轴电压也能快速达到稳定状态，响应时间快，超调量小，具有良好的控制效果。

为了验证各个电机是否达到同步运行状态，对式(7)的输出同步进行研究。不考虑扰动和系统的不确定性，则Hamilton能量函数为

(22)

对H求导可得

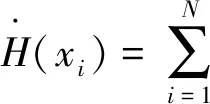
(23)

仅考虑协同控制，控制律式(12)可写成

u=-Q(Y1-Y2)

(24)

(25)

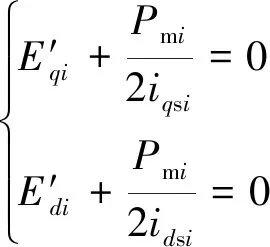
(26)

(27)

则当每台风电机组输出同步时，Psi=Pmi，即各发电机组输入的机械功率相同时，输出的有功功率便相同。双馈风力发电机组在运行状态下，同一区域内容易满足各台发电机组吸收的风能基本相同，因此保证了各台发电机组输出了相同的有功功率。

对各台发电机的输出有功功率进行仿真，如图8和图9所示。

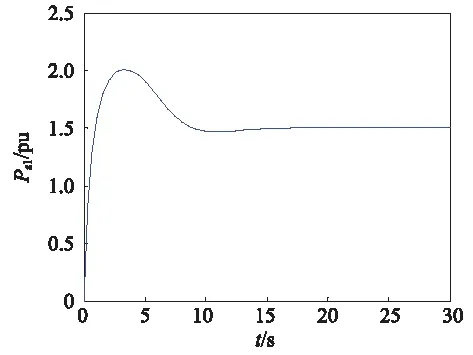
图8 1号发电机输出有功功率的响应曲线Fig.8 The output active power response curve of the first generator

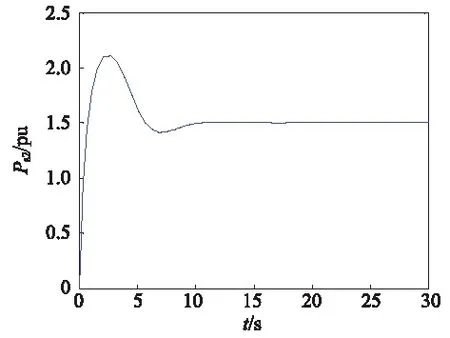
图9 2号发电机输出有功功率的响应曲线Fig.9 The output active power response curve of the second generator

由图8和图9可看出两台发电机输出的有功功率是相同的，证明了所设计的控制器可以使多机系统保持协同稳定运行。

为验证控制器的自适应能力，改变系统参数如下：Htot1=4 s，Htot2=5 s，iqs11.8 pu，ids1=1.6 pu，iqs2=1.6 pu，ids2=1.4 pu，Pm1=Pm2=1.5 pu，对系统再次进行仿真，仿真结果如图10～图17所示。

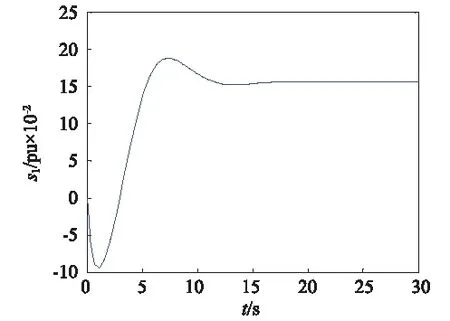
图10 1号发电机转子滑差s1的响应曲线Fig.10 The rotor slip response curve of the first generator

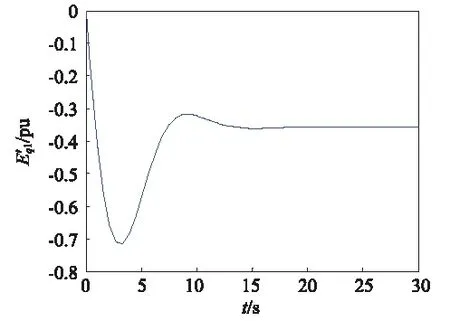
图11 1号发电机q轴电压的响应曲线Fig.11 The transient potential response curve of the first generator in q-axis

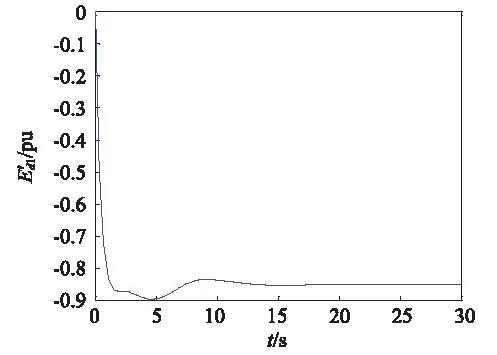
图12 1号发电机d轴电压的响应曲线Fig.12 The transient potential response curve of the first generator in d-axis

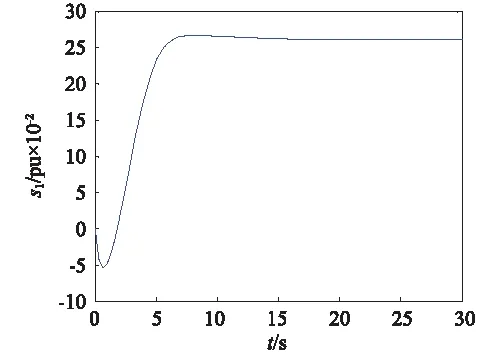
图13 2号发电机转子滑差s2的响应曲线Fig.13 The rotor slip response curve of the second generator

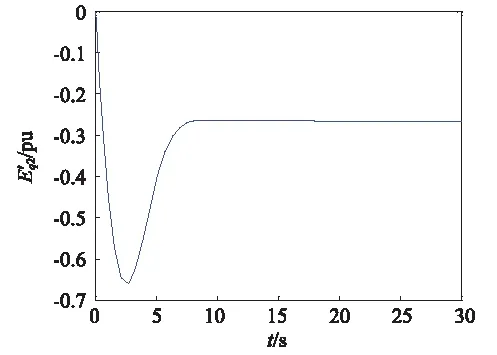
图14 2号发电机q轴电压的响应曲线Fig.14 The transient potential response curve of the second generator in q-axis

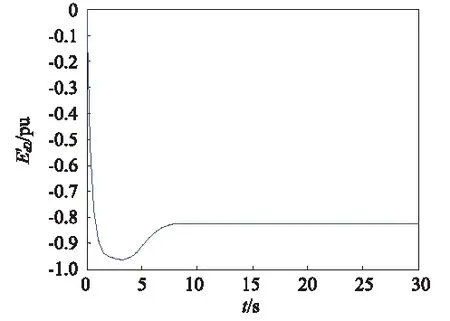
图15 2号发电机d轴电压的响应曲线Fig.15 The transient potential response curve of the second generator in d-axis

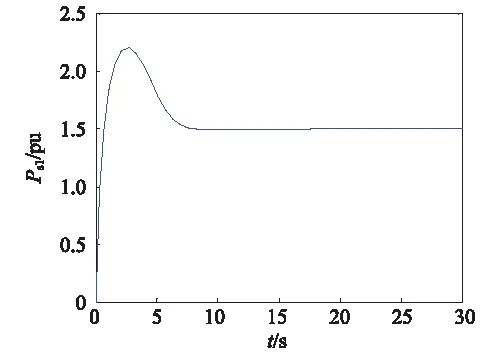
图16 1号发电机输出有功功率Ps1的响应曲线Fig.16 The output active power response curve of the first generator

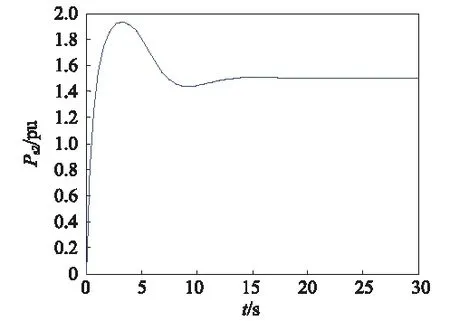
图17 2号发电机输出有功功率Ps2的响应曲线Fig.17 The output active power response curve of the second generator

图10～图17可看出改变参数后，两台发电机组仍能保持稳定运行，并且两台发电机输出的有功功率仍然相同，并未随参数的变化而变化，验证了控制器的自适应能力，可使多发电机组保持协同稳定运行状态。

4 结 论

研究了双馈感应发电机组在既有外部干扰又有结构参数不确定的情况下，基于Hamilton函数的自适应H∞控制问题，使多机系统能够保持协同镇定。首先考虑了多机系统模型Hamilton实现，基于Hamilton能量函数，通过预反馈控制将其表示为端口受控耗散Hamilton系统。随后考虑既有外部干扰又有结构参数不确定的情况，设计一种输出反馈+自适应干扰抑制的同步控制器，使其能够保持多机协同控制，所设计出的控制器具有鲁棒自适应控制性能。仿真结果表明，当存在的外部干扰和参数不确定时，所设计的控制器能够使双馈感应发电机组趋于协同稳定运行状态，有效地提高了电机系统的稳定性，得到了满意的控制效果。