爆炸荷载下锚固洞室拱脚的变形破坏规律研究

2019-08-06杨自友杨本水顾金才

振动与冲击 2019年14期

杨自友，杨本水，顾金才

(1. 安徽建筑大学土木工程学院，合肥 230601； 2. 总参工程兵科研三所，河南洛阳 471023)

地下工程中的洞室的断面形状是多种多样的，如有马蹄形的、半圆拱形的和直墙拱顶形的，等等。这些洞室中往往会存在凸出或凹进的部位，尤其是直墙拱顶形的，直墙与拱顶间的连接之处易形成凹进岩体的棱角，称之为拱脚。拱脚处由于容易产生大变形，再加上岩土体所处的外部环境条件的变化，尤其是受到震动冲击载荷时，常常会发生破坏。学者们对此进行了研究，如信春雷等[1]通过研究显示跨走向滑动断层隧道在地震时，其拱脚处易产生拉应力集中而破坏。施有志等[2]利用数值模拟发现地震力作用下，南、北两线隧道的左拱肩和左拱脚的位移、加速度响应差都比别处的大。胡鸿运等[3]应用波动方法研究顺层隧道的地震响应得知，qP波引起的环向弯矩极值位于拱脚。汪精河等[4]通过研究隧道衬砌与斜入射地震波的相互作用，发现拱顶、拱脚是抗震的薄弱部位。曲宏略等[5]通过能量分析法研究指出，跨断层隧道在断层错动与地震的耦合作用下，拱肩、拱脚的动态响应最大。徐景茂等[6-7]研究了在平面装药爆炸条件下的锚杆加固洞室围岩的应力、拱脚处的变形特征等问题。Mussa等[8]以地表车载炸药爆炸为例，对地下箱形隧洞的破坏情况进行了数值实验研究，并导出了计算每个爆炸箱的大气压峰值压力的公式。Mobaraki等[9]进行了地表爆炸条件下，隧道深度和断面形状的数值分析研究，指出圆形和马蹄形隧道抗破坏能力不及箱形隧道，但半椭圆形隧道比箱型隧道更具抵抗力。Verma等[10]调研了喜马拉雅印度一侧5个隧洞的爆破损伤情况，收集了113个试验爆炸数据，并得到了爆破围岩损伤的经验公式。Yan等[11]应用突变理论对地下洞室群受爆破振动的影响进行了失稳分析，得到了失稳条件并确定了洞室顶底板的临界安全厚度。

总结上述，关于在集中装药条件下，研究洞室拱脚的变形与破坏的成果较为少见。由于拱脚部位较为特殊，受动载作用后，易产生较大的变形破坏，因此，本文将对在集中装药爆炸荷载作用下，锚杆加固洞室的拱脚变形特征及其变化规律、拱脚应变波形进行专门研究，为爆炸条件下的地下洞室拱脚加固措施的改进提供参考依据。

1 模型试验概况

模型试验的原型是处于Ⅲ类岩体中的直墙拱顶形洞室，跨度5 m，埋深20 m，采用φ18螺纹钢筋作为加固锚杆，集中装药当量为500 kg。模型试验中，按照Froude比例法，经过计算，分别选取应力、长度和密度相似比例为Kσ=0.06，KL=0.09，Kρ= 0.67。模型尺寸长×宽×高=2.4 m×1.5 m×2.3 m，洞室跨度60 cm，高度42 cm。洞室沿轴向分为两个试验段，各1.2 m，采用2种锚杆加固方式，加固段长度为600 mm。围岩材料是水泥砂浆，材料及其重量比为∶砂∶水泥∶水∶速凝剂=15∶1∶1.6∶0.016 6，加固锚杆采用铝棒模拟，直径2.1 mm。模型尺寸见图1(a)，Ⅲ类岩体参数及模型材料的物理力学参数见表1。

表1 III类围岩和模型材料物理力学参数 Tab.1 Physico-mechanical parameters of rock III and models materials

图1 模型、洞室加固方式及应变测点布置Fig.1 Model，tunnel reinforcement pattern and strain measuring points configuration

本文研究的洞室较多，因各个洞室都是沿着其纵向轴对称的，故这里仅给出6个洞室横截面的右半部分的锚杆布置平面图，如图1(b)所示。每个洞室每次放炮的集中装药量均为100 gTNT。洞室D1～D3锚杆间距分别是9 cm，6 cm和3 cm，长度都是18 cm，主要研究锚杆间距变化对拱脚变形的影响(称作锚杆间距影响洞室，下同)，而D4～D6锚杆长度分别是6 cm，6～18 cm间隔布置和18～30 cm拱脚局部加长布置，间距都是3 cm，主要研究锚杆长度变化对拱脚变形的影响(称作锚杆长度影响洞室，下同)。

模型试验测试系统如图2所示，由前置传感器、电荷放大器、动态应变仪、数据记录及处理、回放系统等组成。

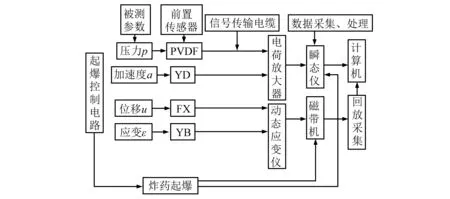
图2 测试系统示意图Fig.2 Schematic diagram of testing system

测量洞室围岩应力使用压电式传感器(PVDF)，洞室顶底板相对位移用差动变压器式位移计，拱顶、底板及侧墙加速度用压电式加速度传感器，压电式传感器信号用电荷放大器进行放大。测量洞壁动应变的传感器为1 mm×2 mm应变片，其信号由动态应变仪进行放大。数据的测试采集采用多通道磁带记录机和瞬态记录仪，回放和处理采用瞬态记录仪。因本文仅研究洞壁变形规律，为简单起见，这里仅给出动态应变仪的基本性能参数，见表2。

表2 动态应变仪性能指标 Tab.2 Performance index of dynamic strain gauge

试验过程是先制作如图1(a)所示的模型，然后开挖洞室，接着布置加固锚杆及各种测量设备，然后进行集中装药爆炸试验与结果分析。

2 试验结果分析

本文的研究思路是先比较第1炮(装药量100 gTNT，埋深50 cm)，典型洞室(选取D1洞室)内部拱脚测点应变与其他部位测点应变的差异性，因此，图1(b)中D1洞室给出了第1、第2炮集中装药与全部6个洞壁应变测点的位置，测点编号为e1～e6，其中e1,e2分别在拱顶、拱腰，e3，e4在拱脚，e5，e6在直墙。然后再比较第2炮(装药量100 gTNT，埋深70 cm)，6个洞室加固锚杆的间距、长度变化对拱脚变形破坏的影响，除了D1洞室，另5个洞室D2～D6仅给出拱脚2个应变测点的位置。需强调的是，拱脚布置了靠得很近的e3，e4两个测点，因e3在拱部，称为拱部测点，e4在直墙部位，称为直墙测点。最后分析6个洞室拱脚最终破坏形态。

对于6个洞室大部分应变测点来说，在40 ms后，应变波形基本保持稳定了，故文中仅给出了时长40 ms的测点应变波形。

2.1 同一洞室拱脚应变与其他部位应变的比较

为了比较拱脚测点与本洞室其它部位测点变形的差异性，避免重复使用数据，这里选取D1作为典型洞室，给出其内部6个测点第1炮时的围岩表面应变波形曲线、应变峰值及其残余值，如图3和表3所示，分析其中6个测点应变波形的变化特征及其规律，由于其它洞室测点的应变变化规律大致与D1洞室类似，故不再赘述。

图3 洞室D1测点应变波形Fig.3 Strain waveform of D1

由图3可看出，D1拱顶测点e1应变波形先急剧上升到正峰值约963(峰值正负仅表示围岩受力状态，正值表示受拉，负值表示受压，大小取其绝对值，下同)，约3.5 ms衰减至0，此过程为拉应变，即拱顶处于受拉状态；然后波形变化到反方向，表示拱顶产生压应变，持续时间稍长，但此过程的压应变值均不大，直到拱顶留下残余应变为止。

除了e1测点外，e2～e6测点的波形基本上反映了在达到压应变峰值以后，随时间推移而逐渐衰减，只是衰减程度各有差别。其中e5,e6测点在6～13 ms还产生了拉应变；e2,e3和e4测点在40 ms内，波形全程是压应变。由图2还可看出，拱脚测点e3，e4波形的应变峰值和残余值均比其余4个测点的大，说明拱脚的变形较其他部位的大。

表3 D1测点应变峰值及其残余值 Tab.3 Strain peak and residual values of measuring points in D1

从表3可看出，在应变峰值方面，测点e1在拱顶部位，其峰值为正，如前所述，说明该处受拉而产生拉应变，由于爆炸应力波向洞室两侧传播，两侧围岩有向两边变形的趋势，从而使得拱顶产生拉伸变形，若能够抵抗这样大小的变形，则拱顶就不会产生破坏；测点e2～e6的应变峰值均为负值，表明洞室中这些部位在与应力波的波峰相互作用过程中产生压应变；6个测点中，由于e6位于洞室直墙的最下端处，应力波强度到达此处已经衰减的很多了，故其应变峰值最小。

由表3可明显看出，拱脚测点e3，e4应变峰值均比其余测点的大，分别是e6应变峰值的近5.9倍、5.6倍，尽管这两个测点都产生压应变，但该处是拱脚部位，是直墙与拱部的交叉点，在爆炸荷载作用下，此处会产生不均匀变形现象，一旦该处的应变峰值超过其所能承受的抵抗变形的能力，那么，拱脚处很容易产生破坏，因此相对于其它位置，拱脚部位应该是整个洞室较容易产生变形破坏的地方。

需要说明的是，表2中所列为模型试验第1炮时的6个洞室洞壁应变，而实际观测未发现拱脚处出现压裂破坏等现象，说明表中应变均未超过各个洞室拱脚所能承受的变形量。

在残余应变值方面，仅测点e5显示出受拉，且其值在6个测点中是最小的，其余测点的残余应变均为压应变；由表1可知，测点e3，e4的残余应变值与其峰值应变相对应，也均比其它测点的大；在残余值大小方面，测点e3，e4比测点e5的大2～3个数量级，这也再次说明拱脚测点处抗变形能力稍差，变形大，且其附近容易产生破坏裂纹。

2.2 不同洞室拱脚测点应变的比较

图4～图7分别给出了6个洞室第2炮拱脚处的拱部测点e3、直墙测点e4的应变波形，并对其进行分析。

图4 锚杆间距影响洞室拱脚拱部测点应变波形Fig.4 Strain waveforms of arch measuring points influenced by rockbolts’ spacing at arch springings in 3 tunnels

图4所示3个洞室D1～D3的拱脚的拱部测点应变波形在快速达到峰值以后，拱脚拱部测点波形距离时间坐标轴(横轴)由远及近的依次是D1e3，D2e3，D3e3，而3洞室锚杆间距的大小顺序依次是D1>D2>D3，即随着锚杆间距的减小，拱脚的变形在减小，表明锚杆间距变化规律与拱脚拱部的变形规律具有一致性。

这3个波形在0～3 ms内达到了应变峰值，峰值大小相差较大，且从大到小的测点顺序依次是D1e3>D2e3>D3e3。各波形随后发生了衰减，D2e3波形衰减的稍快一点，D1e3经历了应变2次增大与减小的变化，达40 ms波形基本稳定了，D1，D2洞室拱脚的拱部在与应力波相互作用的过程中，全部表现为受压变形。

而D3e3在衰减到0后，继续朝着受拉的方向前进，后又转变为受压变形，如此反复下去，40 ms后仍然在继续这种变化，但均在横轴附近震荡且峰值较小。

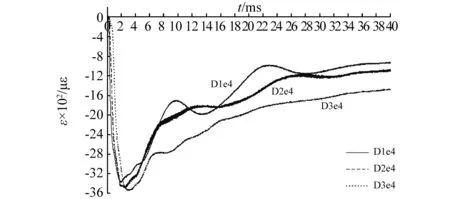
图5 锚杆间距影响洞室拱脚直墙测点应变波形Fig.5 Strain waveforms of sidewall measuring points influenced by rockbolts’ spacing at arch springings in 3 tunnels

由图5可看出，3洞室拱脚直墙部位测点的应变波形与图4所示拱部测点的有较大差别，即随着锚杆间距的减小，3个波形不再是依次向横轴靠近，而是在达到峰值后，均距离横轴较远。约15 ms后，D1e4波形距离横轴比其它2测点的稍近一些，也经历了2次增大～减小的过程，而其他两个波形基本一直在衰减。在1～4 ms内，3测点应变达到峰值，且由图可知，3个峰值大小较为接近，相差不大，说明锚杆间距变化规律与洞室拱脚的直墙部位变形规律不具有一致性。

图6所示3洞室拱脚拱部3个测点波形在快速达到峰值应变后，便产生了衰减，D4e3的波形存在小幅的振荡，D5e3和D6e3波形较为光滑，其中由于D6洞室的加固锚杆最长，采用了拱脚局部加长的布置方式，故D6e3测点的衰减最快，波形距离横轴也最近，说明该处变形比其它2测点都小；3测点波形在0～5 ms内达到峰值，其大小顺序依次是D5e3>D4e3>D6e3，而3洞室的加固锚杆的长度大小依次是D6>D5>D4，说明锚杆长度变化规律与洞室拱脚拱部的变形规律没有一致性，但D6洞室锚杆长度比另2洞室的大，故其拱脚拱部应变峰值比另2洞室小，表明增大锚杆长度能减小洞室拱脚拱部变形。

当加固锚杆间距一定，长度较大时，洞室的拱脚的变形就应该较小一些，图7所示的拱脚直墙部位的3洞室拱脚的测点应变变化规律即是如此。随着加固锚杆长度的增大，3个测点的应变波形在依次向着横轴靠拢，峰值依次减小，其由大到小的顺序是D4e4>D5e4>D6e4，说明锚杆长度变化规律与洞室拱脚直墙部位的变形规律具有相反性。3测点波形在达到峰值应变后，也产生了衰减，在局部发生微小变化后，最终变形减小到残余值。

图7 锚杆长度影响洞室拱脚直墙测点应变波形Fig.7 Strain waveforms of sidewall measuring points influenced byrockbolts’ length at arch springing in 3 tunnels

表4中给出了各个洞室拱脚的两个测点应变峰值及其残余值的平均值。

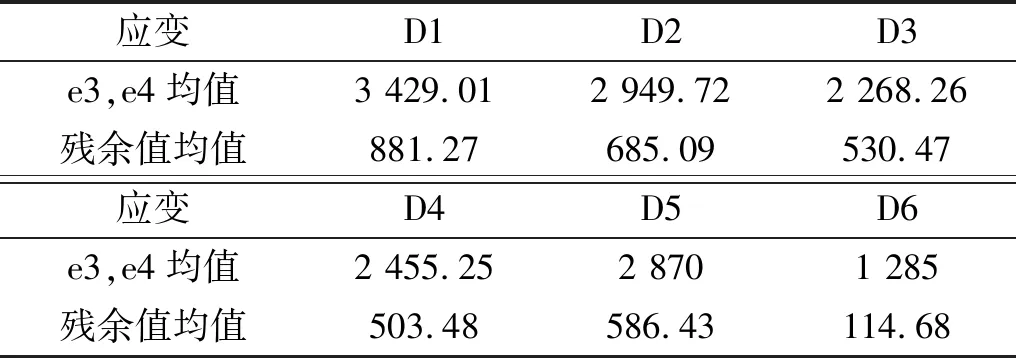
表4 各洞室拱脚应变峰值及残余值的均值 Tab.4 The mean values of strain peak and residual values of arch springings in every tunnel

从表4中容易看出，对于锚杆间距影响洞室D1～D3来说，随着加固锚杆间距的减小，拱脚应变峰值及其残余值的均值也依次减小，说明当锚杆的长度一定时，减小锚杆间距能有效减小洞室拱脚变形，且D3洞室拱脚应变峰值均值分别比D1，D2洞室应变峰值均值小51.2%，30%。而从锚杆长度影响洞室拱脚应变及其残余值的均值来看，拱脚应变峰值及其残余值均值都是先增大后减小，且D4，D5洞室的拱脚应变均值分别是D6洞室拱脚应变均值的1.9倍、2.2倍。由此可知，锚杆间距一定时，D6洞室增加了锚杆长度，其拱脚变形减小的很显著。

2.3 洞室拱脚破坏形态比较

图8所示为6个洞室拱脚的破坏形态，拱脚附近岩体均分布有裂纹，只是分布情况各有不同。

由图8(a)～图8(c)易知，随着加固锚杆间距的减小，3个洞室拱脚部位附近均有破坏裂纹，但分布的位置不同，前两图中的破坏裂纹直接穿过锚杆加固区域向拱脚延伸过来，图8(b)拱脚还产生了较大的断裂，图8(c)的裂纹仅仅位于拱脚锚杆加固区域以外，未穿过加固区域。由此可知，随着间距的减小，锚杆间距影响洞室拱脚部位的破坏程度也在减小，说明锚杆间距对拱脚围岩的破坏范围有影响。

图8 各洞室拱脚破坏形态Fig.8 Failure forms of six arch springings

由图8(d)、图8(e)可看出，由于拱脚的变形较大，洞室上方的破坏裂纹传播到了拱脚附近，由于都采用了短密锚杆加固，裂纹没有穿过加固区域，但由于图8(d)加固锚杆长度过小以及图8(e)中的较长锚杆过于稀疏，使得破坏裂纹距离两洞室太过接近了，所以这两种锚杆加固方式不可取；图8(f)所示为拱脚局部加长的密锚杆加固方式，洞室上方延伸过来的裂纹刚刚到达拱脚第一根加长的锚杆顶端就停止“前进”，没有再向拱脚下方传播了。实际上，图8(c)和图8(f)的长密锚杆加固方式相当于在洞室周围形成了“加固拱”结构，使得拱内部的岩体强度增大了，从而阻止了爆炸能量向“加固拱”内部的传播，提高了洞室拱脚的抗变形能力。

由上分析知，虽然D1，D2洞室的锚杆长度和间距总体上比D4，D5的大，但拱脚破坏裂纹均穿过了前2洞室的加固区域，只有当锚杆间距减小到3 cm时，由图8(c)～图8(f)知，破坏裂纹均未穿过锚杆加固的区域。将D4，D5洞室与D3，D6相比较易知，仅3 cm的锚杆间距而长度过小也存在弊端，即破坏裂纹距离洞室的边缘太近，也不利于洞室的稳定。那么，只有当加固锚杆的间距和长度参数彼此之间“协调一致”时，本文条件是至少要符合D3洞室锚杆布置参数的要求，才能使破坏裂纹远离洞壁产生，若能达到D6洞室的状态则更理想。