长期循环荷载作用下泥炭质土累积变形简化计算方法研究
2019-08-06周正明张先伟
陈 成, 周正明, 张先伟
(中国科学院 武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071)
交通荷载作用下软土地基的长期服役性能是软土工程中的一个重要问题。 长期循环荷载作用下地基土的沉降变形随时间逐渐累加,残余变形受诸多因素影响,如循环荷载水平,频率以及地基土的排水条件等[1]。
目前,计算循环荷载作用下土体累积残余变形的模型可以分为两种。一种是建立较为复杂的本构模型,其大致可分为两类,一类是黏弹性模型,如Hardin-Drnevich 模型[2]和Iwan模型[3]等;一类是弹塑性模型,如运动硬化嵌套面本构模型[4]以及边界面模型[5]等。黏弹性模型数学表述相对简单便于程序化,且计算量较小,在工程实践中应用较多。但此类模型不能反映应变软化、应力路径的影响。弹塑性模型由于其理论严密,可较真实地反映土体在振动荷载作用下每一个循环内的变形特征以及考虑应变软化、应力路径等。但模型计算中一般采用传统的小步长积分方法,因而会产生巨大的计算量,计算效率方面有待进一步的研究。另外一种计算方法是首先在试验或实测资料基础上建立土体累积应变与初始固结状态、静应力状态、动应力及循环次数的关系的拟合曲线,再结合分层总和法等方法来预测土体在动荷载作用下的沉降。如Monismith等[6]建立的累积塑性应变与循环次数间的指数模型,以及在其基础上考虑静强度参数、初始静偏应力等因素建立的修正模型[7]。黄茂松等[8-9]基于临界状态理论,提出了“动偏应力水平”、“相对偏应力水平”概念,归一化地考虑了围压、静偏应力以及动应力等因素的影响,建立了累积塑性应变与累积孔压经验模型。这类方法的好处是无需建立复杂的数学模型,模型参数较少且计算过程简单,工程实用性较强。
不同于地震荷载,交通荷载引起的地层应力幅值较小,但振动持续时间长,累计振动次数非常高,其引起的微振动不像地震那样强烈,一般不会造成地面建筑物的直接坍塌和破坏。但是,这种振动是长期存在和反复发生的,会导致地基沉降或不均匀下沉,影响地面建筑物的安全和使用寿命。因此,对于长期循环荷载作用下土体累积变形的计算,关键不是计算每一次循环荷载作用过程中的变形情况,而是计算长期累积变形量。为此,本文基于前期开展的泥炭质土不排水循环三轴压缩试验结果[10],采用分离型非线性蠕变有限元法对泥炭质土循环累积残余变形简化计算方法进行了研究。根据长期循环荷载作用下泥炭质土累积残余变形发展规律与静荷载下的蠕变趋势相类似的特点,将土体的循环累积残余变形等效为蠕变,基于静力学蠕变有限元求解方法,建立土体循环累积残余变形的有限元计算模型。最后,通过对泥炭质土室内不排水循环三轴压缩试验结果以及地铁荷载下泥炭质土地基的长期变形的数值模拟,验证了该方法的有效性。
1 循环累积变形简化计算方法
1.1 基本假定
目前,静力学蠕变模型(如过应力模型、非稳态流动面模型等)中通常将总应变拆分为可恢复的弹性应变和不可恢复的黏塑性应变。其中,将率相关的蠕变变形与率无关的塑性变形耦合在一起视为不可恢复的应变,虽然一定程度上简化了模型在算法实现上的难度,但物理本质上有待商榷。如Dafalias[11]通过试验研究认为将土体不可恢复应变拆分为率相关部分和率无关部分更加合理。鉴于此,本研究中总应变采用分离型拆分方式,即
(1)
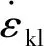
(2)

1.2 弹塑性变形
本研究中,采用临界状态理论计算与时间无关的弹塑性变形。对于弹性变形,其刚度常数为
(3)

对于塑性变形,采用遵循修正剑桥模型的屈服准则以及相关联流动法则,塑性势函数与屈服面函数相同,即
(4)
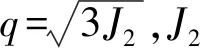
1.3 循环累积变形
根据长期循环荷载作用下土体累积残余变形发展规律与静荷载下土体蠕变趋势相类似的特点[12-14],将土体的循环累积残余变形等效为静荷载下的蠕变。在这一等效方法基础上,通过引入蠕变势函数来描述土体的三维循环累积变形性质,即
(5)
式中:φ为蠕变乘子;f为蠕变势函数。可以看出,在蠕变乘子和蠕变势函数已知的条件下就可以确定土体的循环累积应变速率张量,进而可以确定每一增量步的循环累积变形。
对于蠕变势函数的确定,可取的方法是采用或改进经典弹塑性模型的势函数。目前在黏弹塑性本构模型研究中,普遍将蠕变势函数设置为与塑性势函数相同的形式[15-16]。本文同样采用这一方法,蠕变势函数取为
(6)

(7)

图1 不排水蠕变试验应力路径示意图Fig.1 Stress path in undrained triaxial creep test
上述蠕变势函数确定后,各循环累积应变速率的方向也就随之确定了。若再能确定应变速率的大小,即蠕变乘子,则循环累积应变速率分量的求解将得以解决。一般而言,蠕变乘子的确定方法有多种,如王者超等[17-18]借用等效应力和等效应变概念,建立了等效蠕变速率与等效蠕变应力间的关系,此时蠕变乘子即等于等效蠕变速率的大小。Borja等[19]分别提出了两种方法确定蠕变乘子的大小,一种是基于体积蠕变公式计算体积蠕变率,而后通过式(7)确定出蠕变乘子大小,进而反求出偏蠕变速率。另一种方法恰好相反,先基于不排水偏蠕变公式计算偏蠕变速率,在利用式(7)确定出蠕变乘子大小,进而反求出体积蠕变速率。李兴照等[20]提出的模型中采用了第一种方法,并取得了较好的模拟结果。结合前期开展的泥炭土不排水三轴循环加载试验,同时考虑到长期循环荷载作用下土中存在一定的累积超孔隙水压力导致很难建立准确描述土体累积塑性体积应变的经验公式,本文采用上述Borja等提出的第二种方法,具体方法如下。首先,利用式(5)将偏应变速率张量表述为
(8)
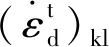
(9)
(10)
此时,有
(11)

由式(9)和式(11)可求出蠕变乘子φ,即
(12)
结合式(5)和式(12),则土体的三维循环累积应变速率张量可表述为
(13)
1.4 硬化规律

(14)
式中:θ=(1+e)/(λ-k),λ为e-lnp空间中压缩线斜率。
对于不排水循环三轴试验,可将动偏应力qd等价为静力不排水三轴蠕变试验中的偏应力q,其应力路径可采用图1 中OAB表示,其中OA段表示第一次循环中的加载过程,并将这一过程视为率无关的弹塑性变形过程,而AB段表示率相关的循环加载过程。土体状态由O点变化到A点时,土体发生塑性硬化,前期固结压力由pcO发展到pcA;随后,当土体状态由A点变化到B点时,这一过程中平均有效应力逐渐减小,应力状态点均位于屈服面内部,土体只发生时间硬化,前期固结压力由pcA发展到pcB。
2 数值实现
与经典弹塑性问题不同,率相关问题的数值分析需对时间项进行离散化, 即在离散的时刻上进行各种力学参量的计算。
2.1 应力积分算法
率相关问题中,土体的应力应变关系可表述为
(15)

(16)

(17)
对于这一典型的弹塑性问题,本文采用隐式图形返回算法进行积分点的本构积分[21],并给出一致性切线刚度张量。主要思路为:

(18)

步骤2利用试探应力速率张量,并结合前一增量步结束时的应力应变状态,检查土体是否发生屈服。若F≤0,土体没有进入屈服状态,试探应力即为最终应力,一致性切线刚度张量就是弹性刚度张量。返回步骤1,进行下一步长的计算;若F>0,表明土体发生屈服,进入下一步骤;
步骤3根据隐式图形返回算法,通过推导可得
(19)
(20)
式中:Δt为增量步的时间增量;dφ为增量塑性乘子,可通过塑性一致性条件求取,即将式(19)~(21)代入式(4),有
(22)
随后,利用 Newton-Raphson 迭代方法求出dφ大小。据此,可更新应力张量和一致性切线刚度张量。返回步骤1,进行下一步长的计算。
2.2 程序实现
借助大型商业软件Abaqus提供的用户子程序接口,将上述应力积分算法编写成UMAT子程序。UMAT子程序主要任务是根据Abaqus主程序导入的应变增量确定出应力增量,并更新相应的状态变量,同时给出材料的雅克比矩阵。基本流程为:首先,计算出时间增量步Δt内的循环累积应变,并将循环累积应变从总应变增量中去除,将率相关问题转化为率无关问题;随后,利用隐式应力积分算法确定积分点应力状态,并更新弹、塑性应变等状态变量;最后,将更新后的应力状态下的一致性切线刚度矩阵赋值给雅克比矩阵数组。
3 方法验证
为了验证上述基于静力学蠕变理论的土体循环累积变形简化计算方法的适用性与稳定性,本文对昆明泥炭质土不排水循环三轴试验结果以及地铁循环荷载作用下泥炭质土的长期变形进行数值模拟。
3.1 泥炭质土累积塑性应变速率
泥炭(质)土是由古生物残体在缺少空气的条件下经过复杂生物化学过程以及数万年的地质作用形成的特殊类软土,是昆明市区广泛分布的软土地层,具有高有机质含量、大孔隙比、高天然含水量、低承载力、高压缩性等较差的工程地质特性。作者曾对昆明泥炭质土开展了系统的循环三轴压缩试验,其中不同围压下循环荷载引起的累积塑性应变与循环周次曲线如图2所示。图中ηd为循环应力比,定义为循环偏应力幅值与土样固结压力之比。基于双对数坐标下累积应变速率与循环周次间的线性关系,陈成等研究中建立了试样轴向累积塑性应变与动荷载循环周次间的经验关系,即
(23)
式中:a,b,m和n1为模型参数;N为循环周次;qd为循环偏应力幅值;qf为静破坏偏应力;qs为循环偏应力基准值,用于描述非双向正弦模式的单向循环加载。它与天然地基土中非等向固结引起的静偏应力不同,前者属于循环荷载的一部分。为了描述静偏应力的影响效应,借鉴Chai等的模型,将式(23)进一步扩展为
(24)
式中:qs0为静偏应力,反映了土体的固结偏应力状态;n2为模型参数,Chai等的模型中建议n2=1。
此外,对于静破坏偏应力qf,有
(25)

将式(24)中的循环荷载作用次数看作时间度量单位,求导后可得出轴向循环累积应变速率,将其代入式(13)即可利用上述UMAT子程序进行计算。实际计算中,循环荷载引起的累积变形计算分为三步。第一步是地基土初始应力的确定,包括地基土的围压水平、固结偏应力状态以及静抗剪强度等;第二步是只施加一次循环荷载,用于获取地基土中循环应力幅值的分布情况。在前两步的基础上,第三步进行地基土累积变形的计算。
3.2 单元试验模拟
有限元分析中,采用 1/4 土样尺寸(直径39.1 mm、高度80 mm)的几何模型,单元类型为二阶20节点三维实体单元(C3D20)。按照荷载控制方式进行加载。首先,建立初始的自平衡应力状态;然后在试样顶部按静力方式施加与动偏应力相等的荷载,最后进行循环累积变形计算。
模型计算参数包括率无关的修正剑桥模型参数以及循环累积应变经验模型中的拟合参数。针对昆明泥炭质土,模型计算参数如表1所示(修正剑桥模型参数λ和κ通过一维压缩试验,参数M通过不排水三轴压缩试验确定)。
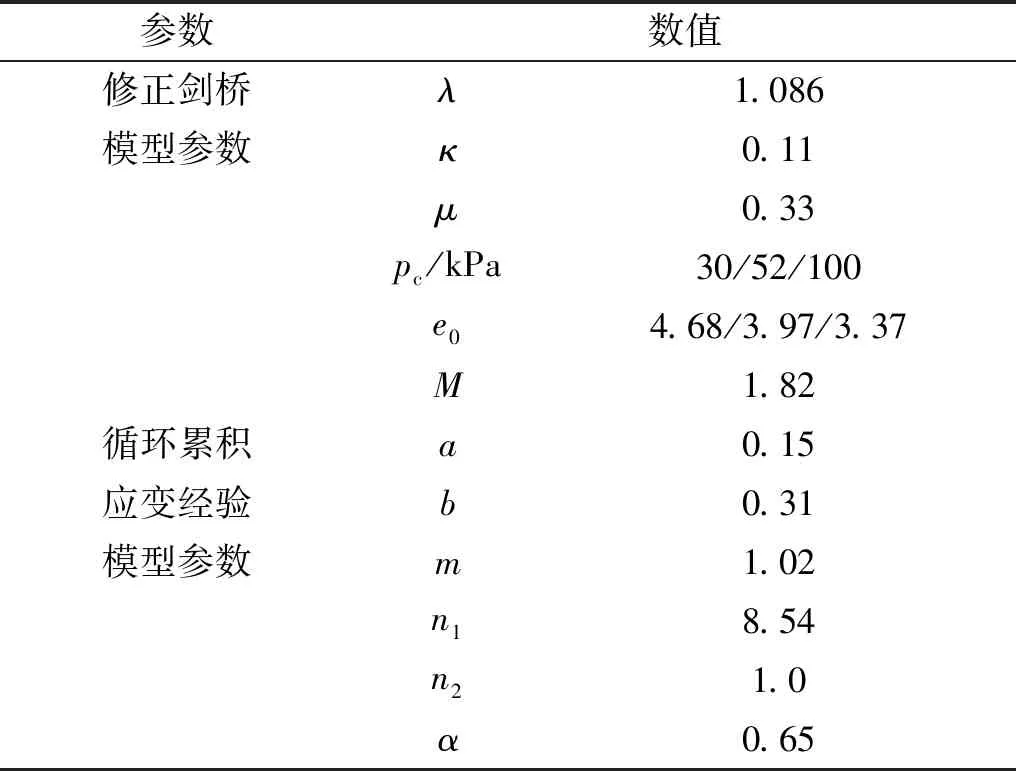
表1 模型参数汇总 Tab.1 Summary of model parameters
数值计算结果与实测结果对比同样见图2。可以看出,不同围压和动偏应力水平组合试验条件下,有限元计算结果与实测值相对吻合,表明本文提出的基于静力学蠕变理论的土体循环累积变形简化计算方法可以很好地描述循环偏应力水平以及围压水平对泥炭质土试样循环累积变形特性的影响规律。

图2 循环累积应变与循环次数关系Fig.2 Accumulated strain versus number of cycles
3.3 地铁荷载下泥炭质土的长期变形模拟
采用平面应变模型模拟地铁循环荷载作用下泥炭质土地基的长期变形。考虑隧道结构对称性,取一半隧道以及土体进行计算。计算几何模型和网格划分如图3所示,包括地基土,隧道衬砌以及泥浆等代层。其中,隧道埋深8.8 m,隧洞直径6.2 m,衬砌和等代层的厚度分别为0.35 m和0.1 m。模型水平方向长度为5倍的洞径,即31 m。竖向为30 m,包含三层地基土,分别是7 m厚黏土层,13 m厚的泥炭质土层以及10 m厚的粉砂下卧层。有限元模型共包括1 655个4节点完全积分平面应变单元(CPE4)。土体的边界条件为左右两边水平方向位移约束,底部为竖向位移约束。同时在泥炭质土层与粉砂层间设置透水边界条件。计算过程中,只考虑泥炭质土层的循环累积变形特性,计算参数如表1所示,其中e0取为4.68。黏土层采用修正剑桥模型,计算参数分别为:λ=0.173,κ=0.034,μ=0.33,e0=1.40以及M=1.22。粉砂层采用摩尔库伦模型,计算参数分别为:压缩模量E=13.5 MPa,μ=0.29,c=5 kPa以及φ=28°。
整个计算过程共分为4个步骤,即:①地应力平衡,确定地基土初始围压、静偏应力水平以及土体的静力强度等;②隧道开挖与支护;③施加一次地铁运行引起的动荷载,获取地基土中循环应力幅值;④地铁荷载下地基土累积变形计算。对于地铁运行引起的动荷载,按行驶速度80 km/h计取为69 kPa,作用于宽度为1.44 m的轨道上[25]。

图3 有限元网格划分Fig.3 Finite element mesh
图4 给出了泥炭质土层中循环偏应力幅值的分布云图。可以看出,隧道底部地基土所受到的循环应力幅值最大。随与隧道距离的增加,循环应力逐渐减小。
隧道上方以及远场地基土所受到的循环应力均趋于0。图5给出了地铁运行2 000 000引起的地基土竖向位移分布(不包括隧道开挖引起的竖向位移)。图6给出了隧道底部以及隧道正上方地表的沉降历时曲线。其中,地铁运行按年平均20 万次计。可以看出,隧道底部的沉降量大于隧道上方地表的沉降量。随着运行时间的增长,两者的沉降量均逐渐增加,且增长速率逐渐减小。在运行2年、4年、6年、8年、10年情况下,隧道正上方地表的沉降量分别为1.14 cm,1.73 cm,2.19 cm,2.58 cm,2.92 cm。此外,列车运营荷载引起隧道结构发生下沉,进而使隧道上部土体产生变形,包括竖向沉降和朝隧道结构方向的水平向位移,浅层土体朝隧道结构方向的水平向位移一定程度上阻碍了其沉降的趋势,因而导致隧道底部沉降略大于隧道正上方地表沉降。高静连[26]也得出了类似的计算成果。
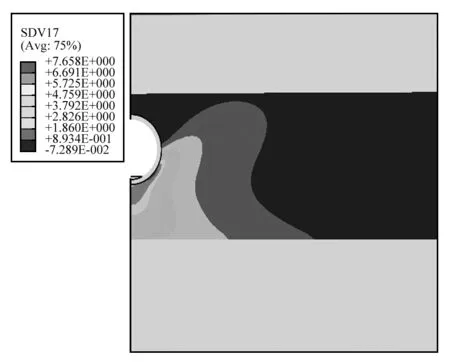
图4 循环应力分布Fig.4 Distribution of cyclic stress
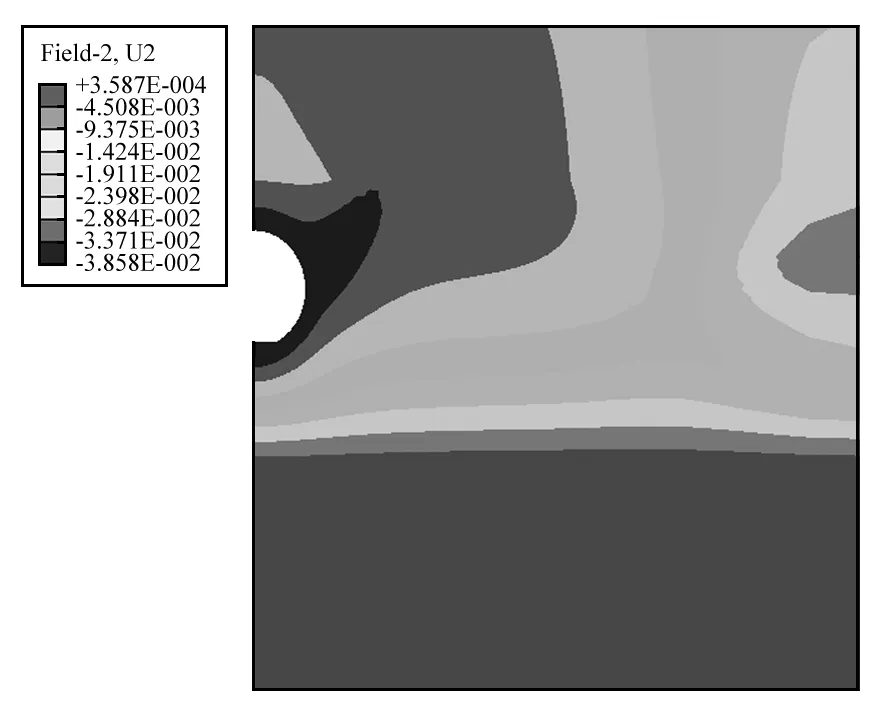
图5 地铁运营引起的沉降分布Fig.5 Distribution of settlements induced by subway operation

图6 沉降时间曲线Fig.6 Settlements versus time
4 结 论
基于长期循环荷载作用下土体累积残余变形发展规律与静荷载下土体蠕变变形规律相似的特点,提出了长期循环荷载作用下土体累积变形简化计算方法,得出如下结论:
(1) 基于临界状态理论,将土体循环累积残余变形等效为静荷载下的蠕变,同时将循环荷载作用次数看作时间度量单位,通过引入与修正建桥模型屈服面一致的蠕变势,结合不排水条件下土体偏循环累积应变经验模型,建立了可描述土体三维循环累积变形的简化方法。
(2) 分项考虑率相关循环累积应变与率无关弹塑性应变,并利用隐式图形返回算法进行本构积分。在此基础上,基于Abaqus二次开发接口,编制了UMAT子程序。
(3) 采用提出的循环累积变形简化计算方法对昆明泥炭质土不排水循环三轴试验结果以及地铁荷载下泥炭质土地基的长期变形特性进行了数值模拟,验证了该方法的适用性与稳定性。
循环荷载作用下地基土的变形增长与所受临界动应力水平、循环速率频率等因素密切相关,本文后续研究将进一步探讨这些因素对昆明泥炭质土的循环累积变形的影响,并将其量化扩展至式(24)中,进而使本文提出的计算方法在实际应用中可反映这些因素的影响。
