大跨桥梁台风风场全过程动态数值模拟
2019-08-06刘焕举黄平明韩万水刘晓东
武 隽, 刘焕举, 黄平明, 韩万水, 刘晓东
(1. 长安大学 公路学院,西安 710064; 2. 河北工程大学 土木工程学院,河北 邯郸 056038)
当前桥梁呈现大跨化、轻型化的发展趋势,对风作用越来越敏感。沿海地区台风灾害频发,风速较大且变化较快,风向瞬时变化,台风作用下的大跨桥梁安全评估势在必行,台风风场的合理模拟是关键。对桥梁来说,台风风场模拟与良态风的区别主要表现在三个方面:风向时变性、风场的衰减和风速的非平稳性。已有台风风向模拟主要沿用良态风模式,即假设风向垂直于桥跨方向不变[1-3],忽略台风风向的时变性。但台风是圆形或近圆形的热带气旋,台风经过桥梁时,随着台风移动,桥梁各节点风向不断变化,且随着桥梁跨径的增大,节点间风向差别也越来越大,这与已有的桥梁所有节点风向固定且均垂直于桥跨的假设存在根本差异。且随着千米级大跨径桥梁的建设,台风经过桥梁时段明显变长,台风衰减亦需进行充分考虑。
台风风速模拟方面,目前主要是通过改变经典风谱中的参数[4]或是基于进化谱进行模拟[5-9]。改变经典风谱中的参数方法,操作便捷,但经典功率谱是通过实测分析大量具有平稳特性的良态风数据得到,而台风风速具有明显的非平稳特性,因此模拟结果与实际风场偏差较大。进化谱模拟方法,虽然可考虑台风非平稳特性,但该方法中的时变平均风速的获取主要基于实测或假设服从某三角函数分布。实测方法操作繁琐,不可控因素较多且主要用于灾后分析,不能用于风场预估。假设服从某三角函数分布的方法主要用于理论方法探索,适用性较小,且台风运动过程中,由于能量耗散,强度不断衰减,而三角函数无法考虑台风衰减。因此建立考虑风向时变、台风衰减和风速非平稳的大跨桥梁三维风场全过程系统模拟方法亟待进行。
本文首先建立桥梁节点台风风速模拟方法,基于Batts风场模型、台风衰减模型和平均风剖面模型,对时变平均风速进行模拟,采用进化谱理念改进谐波合成法,模拟台风脉动部分。其次采用几何方法,建立了分阶段确定桥梁节点台风时变平均风向方法,并集成风速、风向模拟方法构建大跨桥梁三维台风风场动态模拟框架。最后选取典型大跨斜拉桥为例,进行了台风三维风场模拟方法的适用性研究。
1 桥梁节点台风风速模拟
台风风速是一个源于时变均值、时变方差的极端事件,具有明显的非平稳特性。台风风速模拟研究中,台风风速可表示为时变平均风速模拟和脉动风速两部分之和
U0(t)=U(t)+u(t)
(1)
式中:U0(t)为t时刻台风风速;U(t)为时变平均风速;u(t)为脉动风速。
因此台风风速模拟过程也可划分为时变平均风速模拟和脉动风速模拟两个部分。
1.1 时变平均风速模拟
Batts模型是目前发展较为成熟的风场模型,在平均风速模拟方面,具有较高的准确性[10]。采用Batts模型,考虑台风衰减和风剖面风速变化对时变平均风速进行模拟,依据台风中心与桥梁节点的时变位置关系确定台风经过桥梁全过程的桥梁各节点的时变平均风速时程。
气象学中,常把台风风场看作轴对称的圆形漩涡来进行分析,台风的等温线和等压线近似于一组围绕中心的同心圆,因此在模拟过程中,假定台风风场范围为轴对称的圆。确定风场内各点时变平均风速,首先需建立风场能量衰减模型,确定风场中心气压差的衰减规律;其次可通过确定最大梯度风速Vgri和最大风速半径Rmax,依据各点与台风中心的距离求得风场内各点时变平均风速,该时变平均风速为海平面10 m高度处的时变平均风速;最后进一步采用海平面与地面的风速转化关系和风剖面模型,确定各高度处的桥梁节点时变平均风速。
1.1.1 风场能量衰减模型[11]
台风登陆后在运动过程中能量不断耗散,强度不断衰减,中心气压差不断减小,登陆t时刻后的中心气压差为Δp(t)
Δp(t)=Δp0-0.675(1+sinφ)t
(2)
式中:Δp0为台风登录前中心气压差;φ为登陆海岸线与台风运动方向夹角;t为登陆时间。
1.1.2 风场内各点时变平均风速
台风最大风速半径Rmax是气旋中心到其最强烈风带之间的距离,由于台风衰减,中心气压差不断减小,最大风速半径具有时变性,表达式为[12]
Rmax(t)=exp(-0.123 9Δp(t)0.600 3+5.103 4)
(3)
式中:VRmax(t)为时变平均最大风速,一般出现于时变最大风速半径处,为
VRmax(t)=0.865Vgri(t)+0.5VT
(4)
式中:VT为台风整体移动速度;Vgri(t)为时变最大梯度风速。
梯度风速为气压梯度力造成的空气流动速度,时变最大梯度风速Vgri(t)为
(5)
式中:K为常系数,通常取为6.72;f=2ωsinφ,为地球自转科氏力系数,ω为地球自转角速度,φ为地理纬度。
则风场内与台风中心距离为r(t)的节点风速为
(6)
式中:Vr,in(t),Vr,out(t)分别为桥梁节点与台风中心的距离r(t)小于和大于Rmax(t)的风速;x为与台风沿径向强度衰减有关的参数,在0.5~0.7的变化。
1.1.3 地面与海面平均风速转化关系
台风登陆后,受地表障碍物的影响强度不断减弱,地面10 m高度处平均风速与海面10 m高度处平均风速转化关系为[13]
(7)
式中:Vert(10)为地面10 m高度处10 min内的平均风速;Vr(10)为海面10 m高度处10 min内的平均风速;C为障碍因子;z0为地面粗糙长度。
1.1.4 风剖面模型
不同高度处的台风平均风速计算,可采用指数律风剖面经验模型[14]
(8)
式中:Vert,z为z高度处的平均风速;Vert,z1为z1高度处的平均风速;α为路面粗糙度参数。
1.2 脉动风速模拟
对于良态风一般将平均风速视为常数,采用谐波合成等方法对其脉动风速进行模拟。台风风速变化较快,平均风速具有明显的时变性,在整个模拟时长内,不能再视为常数,因此在台风脉动风速模拟时,基于进化谱理念,对谐波合成法进行改进,随着时变平均风速变化更新风功率谱,实现对台风非平稳特性的模拟。
把风场模拟时长T离散成p个足够短时间间隔Δt,T=pΔt,因为Δt足够短,每个Δt内的风速均可近似视为零均值平稳随机过程,每个Δt内任意时间点的平均风速均可视为该时间间隔内的平均风速,即为时变平均风速,例如在t~t+Δt内,时变平均风速可表示为U(t)。因此台风脉动风速模拟分为两步:①在每个时间间隔Δt内,采用谐波合成法模拟零均值稳态脉动风速,实现每个时间间隔Δt内的脉动风模拟;②在不同时间间隔中,随着时变平均风速变化更新风功率谱,实现不同时间间隔内的脉动风速模拟。
1.2.1 时间间隔Δt内的脉动风速模拟
由于时间间隔足够短,时间间隔内的脉动风速视为零均值平稳高斯随机过程,因此每个时间间隔内的脉动风速可基于经典风谱,直接采用谐波合成法进行模拟。
以z高度处的节点i为例,t~t+Δt内的脉动风速为
(9)
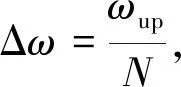
在模拟过程中,水平顺风向风功率谱和横风向风功率谱常采用Simiu谱,竖向风功率谱采用Lumley-Panofsky谱[15],不同方向风场模拟时,只需替换成相应方向风谱即可。由于篇幅限制,下面只对水平顺风向进行说明,则该时间间隔t~t+Δt内的风功率谱为
(10)
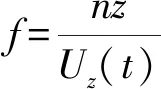
1.2.2 不同时间间隔内的脉动风速模拟
在不同时间间隔,通过实时更新式(10)风谱中时变平均风速,得到每个时间间隔内的时变风功率谱,进而获取不同时间间隔内的脉动风速。
在分别实现台风时变平均风速和脉动风速的模拟的基础上,取台风时变平均风速与相应时间间隔内的脉动风速之和,即实现了台风风速的模拟。
2 桥梁节点时变台风风向确定
由于台风与桥梁位置的相对移动,在台风经过桥梁的时间段内,桥梁各节点的风向随台风移动在不断变化。确定台风经过桥梁时段桥梁节点的时变风向时,做出如下假定:①台风风向规律变化;②该时段内台风保持匀速直线运动。下面以台风中心经过桥跨典型工况为例,建立台风经过桥梁全过程的桥梁节点时变风向确定方法。
2.1 阶段划分
线段AB为桥梁主梁纵向中线,点G为台风眼运动路径与桥跨交点,简称“运交点”,圆为台风风场范围,忽略圆外风场,如图1所示。为便于分析,设沿桥梁轴线右向为正方向,依据桥梁节点来流风向的不同,把台风经过桥梁时段分为4个阶段:第一阶段,桥梁全跨受来流方向为主梁右侧的风作用,桥梁全跨节点逐渐进入风场;第二阶段,AG内的节点风向逐渐由右侧变为左侧;第三阶段,GB内的节点风向逐渐由右侧变为左侧;第四阶段,桥梁全跨受来流方向为主梁左侧的风作用,桥梁全跨节点逐渐移出风场。
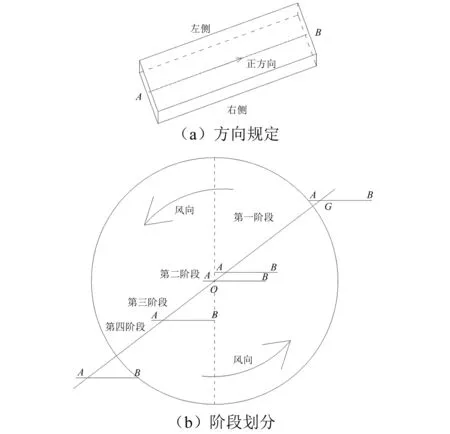
图1 台风经过桥梁区域全过程阶段划分Fig.1 Stage division during typhoon passing through bridge area
2.2 参数定义
m(t)为t时刻台风中心到运交点的距离,α为台风运动方向与桥梁轴线的夹角,γ为台风中心与桥梁最左端节点连线和桥梁轴线的夹角,台风运动速度为v。θi,j,k为所求风向节点与台风中心的连线与桥梁轴线的夹角,设桥梁轴线向右为正,βi,j,k节点风向与桥梁轴线正方向之间的夹角,i=1,2,3表示阶段编号,j=z,y表示在运交点左侧和右侧,k=l,r表示在垂足F左侧和右侧,如图2和图3所示。
2.3 节点风向确定
当台风风场范围与桥梁最左侧节点接触,即桥梁将要进入台风风场范围时,如图2所示,图中
(11)
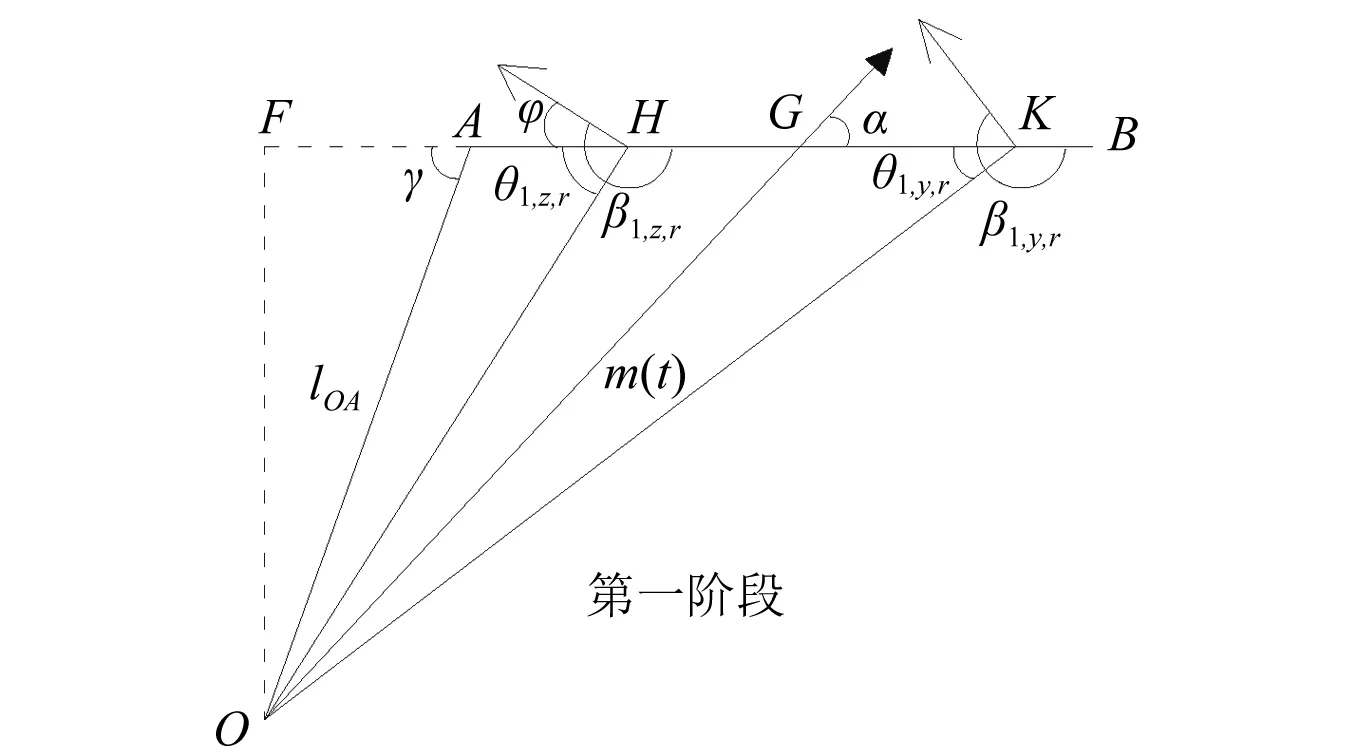
图2 第一阶段风向确定Fig.2 Determination of wind direction in the first stage
此时台风中心距离运交点的距离为
(12)
在台风运动时间t时,台风中心距离运交点距离为
m(t)=m(0)-vt
(13)
2.3.1 第一阶段
(14)
(a)运交点G左侧桥梁节点H
(15)
(b)运交点G右侧的桥梁节点K
(17)
(18)
2.3.2 第二阶段
(19)
(a)运交点G左侧
①垂足点F左侧节点H风向
(20)
(21)
②垂足点F至运交点G之间的节点H’风向可采用式(16)计算。
(b)运交点G右侧桥梁节点K风向可采用式(18)计算。
2.3.3 第三阶段
(22)
(a)运交点G左侧节点H风向
(23)
(24)
(b)运交点G右侧
①运交点G至垂点F的节点K风向
(25)
(26)
②垂点F右侧节点N风向
(27)
(28)
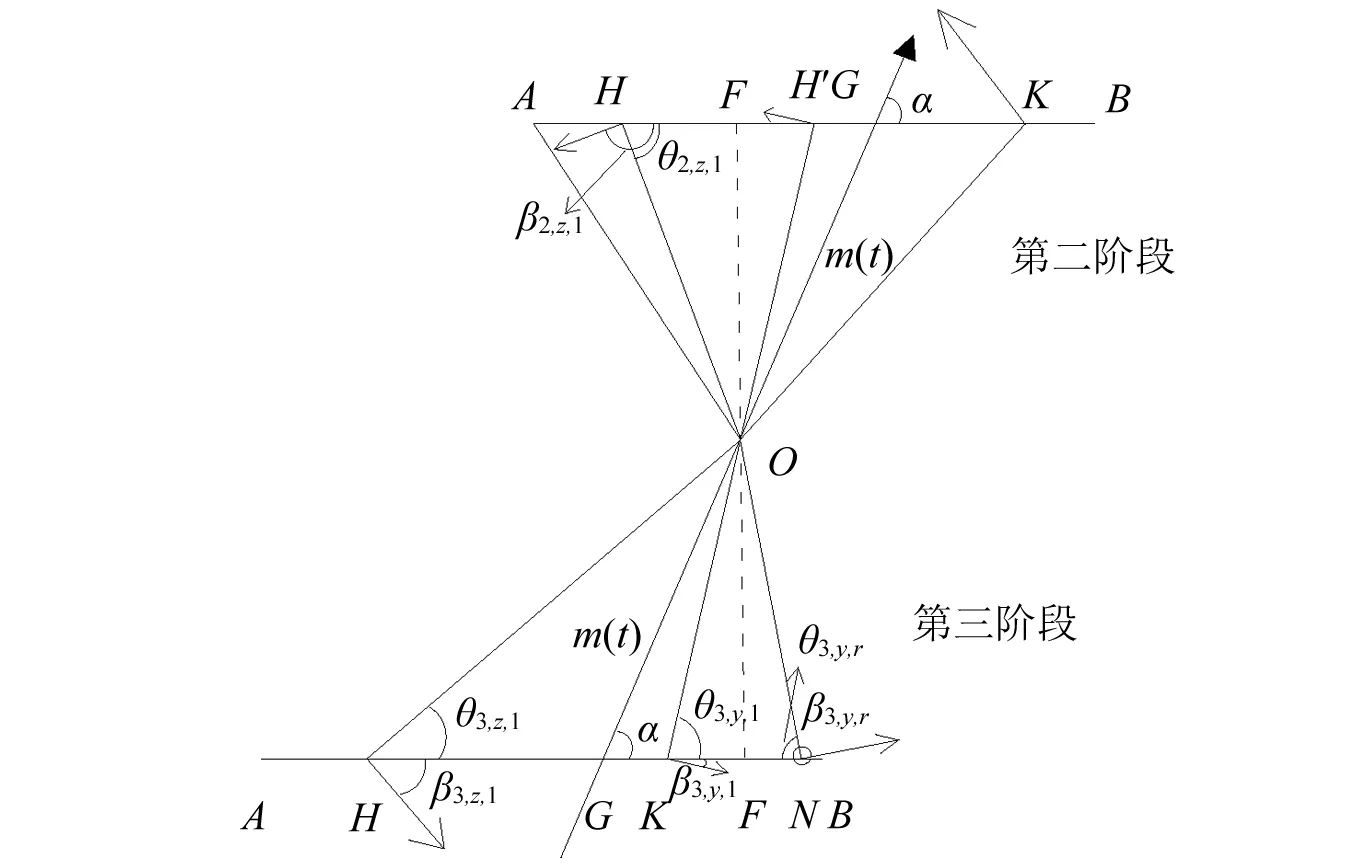
图3 第二、第三阶段风向确定Fig.3 Determination of wind direction in the second and third stage
2.3.4 第四阶段
(a)运交点G左侧节点风向采用式(24)计算。
(b)运交点G右侧节点风向采用式(26)计算。
当台风中心运动路径不经过桥梁跨径时,包括桥梁跨径在路径左侧和右侧两种情况,桥梁节点时变风向可分别参照运交点左侧、右侧节点风向的确定公式进行确定。
3 大跨桥梁台风全过程风场模拟
3.1 桥梁基本资料
选取桥址位于台风频发沿海地区的典型大跨斜拉桥为工程实例,对该桥台风全过程三维风场进行模拟。该斜拉桥为设计跨径908 m的钻石型双塔空间双索面五跨连续钢箱梁斜拉桥,如图4所示。气象调查显示该桥桥位处气象条件复杂多变,台风、雷暴等突发性灾害天气时有发生,仅2016年就遭受了“莫兰蒂”、“马勒卡”等一系列台风侵袭。
3.2 参数确定
对全桥三维风场的模拟,选取了14个典型的模拟点:其中沿跨度方向选取了10个点,各模拟点间距为D=[101,101,101,101,100,101,101,101,101]m;每个桥塔沿塔的高度方向各选取了两个点,具体位置为桥塔顶点及桥塔顶点与主梁中心线连线的中点,模拟点布置如图4所示。
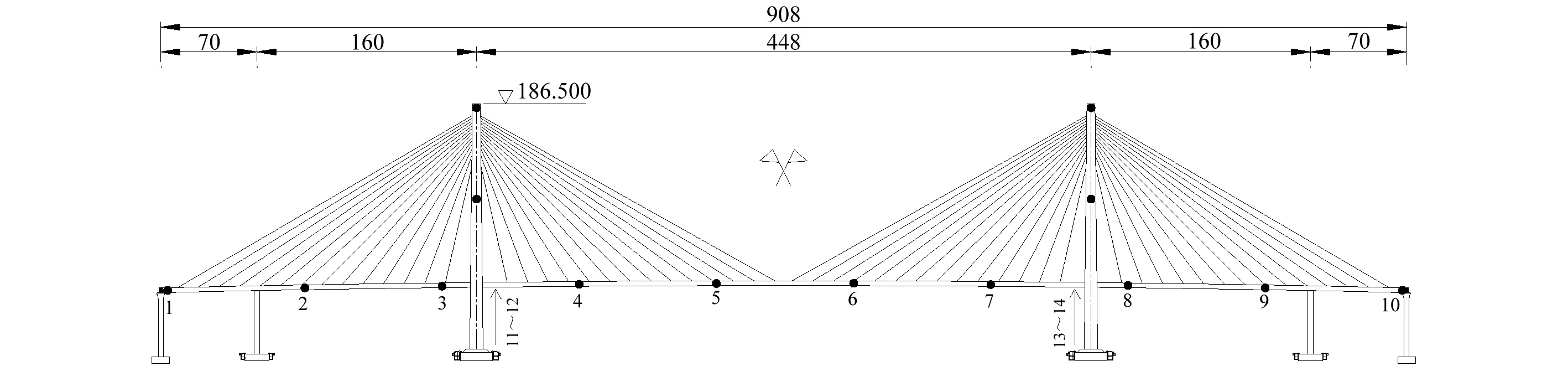
图4 实例桥梁立面图及台风模拟点布置(m)Fig.4 Elevation and arrangement of typhoon simulation points of the bridge example (m)
模拟计算的主要参数如下:跨度L=908 m;主梁离地高度z=54 m;地面粗糙度z0=0.03;模拟点数m=14;截止频率ωup=4π rad/s;频率等分数N=1 024;模拟采样时距dt=0.5 s;风剖面采用指数律模型,指数α取0.03。不同节点处的台风相干函数采用Davenport形式,λ为衰减系数,取7[16]。中心气压差Δp=10 hPa;登陆海岸线与台风运动方向夹角φ=π/4;台风登陆时间t=2 h;地理纬度φ=30°;与台风沿径向强度衰减有关的参数x=0.7;障碍因子C=0.85;台风运动方向与桥梁轴线的夹角α=π/4;
3.3 桥梁典型节点风场模拟分析
基于提出的台风经过桥梁全过程的大跨桥梁台风三维风场动态模拟系统方法,对桥梁风场进行模拟,选取典型节点模拟结果进行分析。
3.3.1 风速模拟
(a)时变平均风速
采用第1.1节中的时变平均风速模拟方法,考虑台风衰减和风速沿风剖面的变化规律,对桥梁节点的台风时变平均风速进行模拟,限于篇幅,选取第2、第9、第11三个典型点进行分析。
由图5可知,时变平均风速总体呈对称“M”型,但并不是完全对称,由于台风在运动过程中的衰减,后半部分值略小;两个极大值出现于各自对应的最大风速半径处;模拟时变平均风速规律与台风结构和实测台风风速规律相同。由于台风在运动过程中能量不断衰减,台风眼与最大风速之间的时变平均风速随时间呈凹曲线变化。由于各节点空间位置的不同,最大平均风速通过各节点的时间不同,但台风尺寸相对于桥梁跨径太大,因此最大平均风速通过各节点的时间差异不明显。风速沿竖向高程的变化较为明显,高程越大,风速越大。
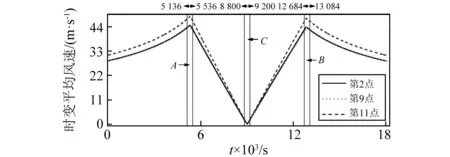
图5 典型点时变平均风速Fig.5 Time-varying mean speed of typical points
(b)脉动风速
采用提出的改进的谐波合成法,基于模拟的各节点时变平均风速,考虑节点间风速的相干性,对大跨桥梁三维风场进行模拟。限于篇幅,选取典型节点(图4中第2、第9点)及典型时间段(图5中A和C时间段)的风场模拟结果进行分析。
由图6可知,各时间区段台风风速总体趋势与时变平均风速趋势相同,风速时程曲线围绕时变平均风速上下波动,时变平均风速越大,振幅越大,反之亦然。
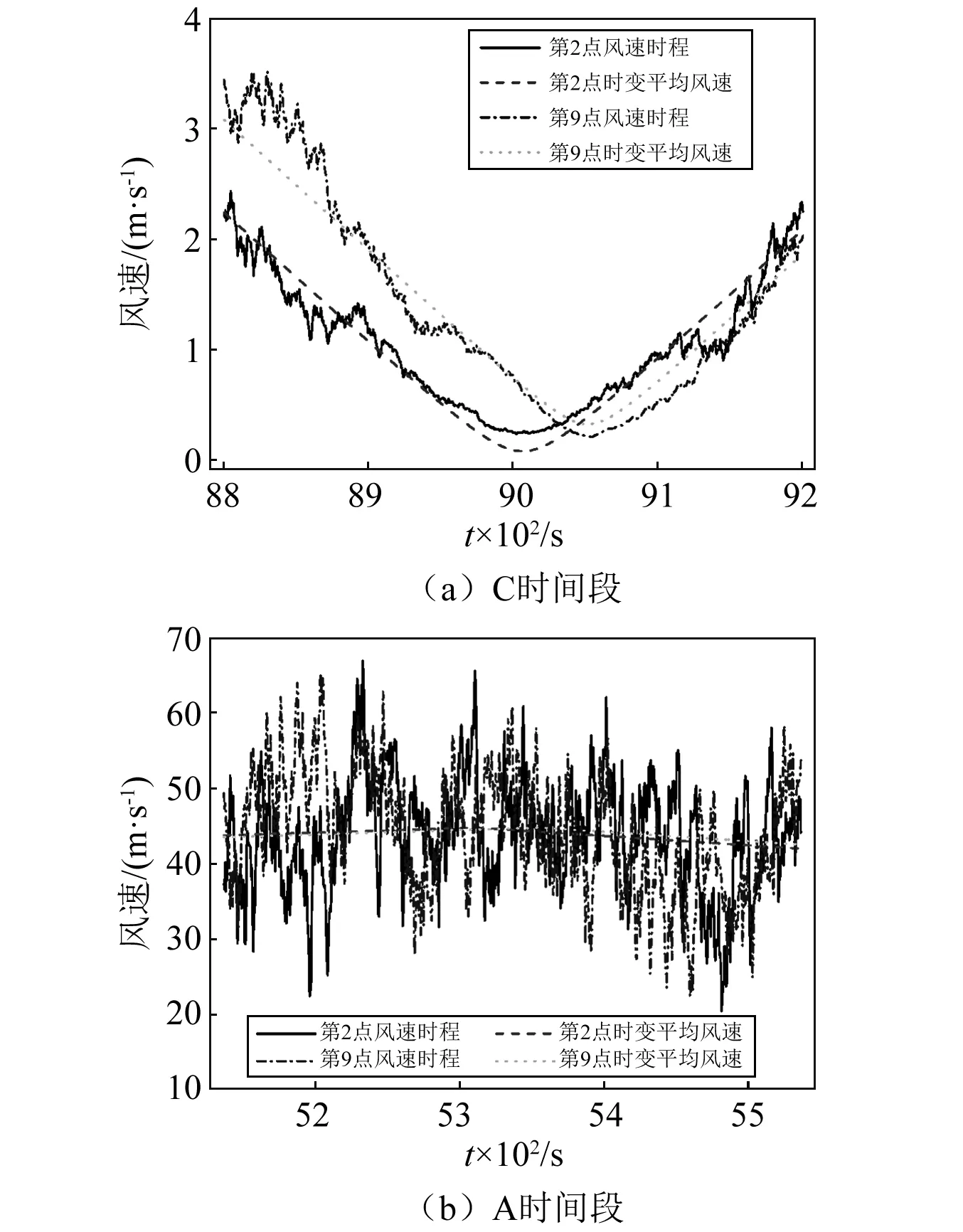
图6 第2、第9点台风风速Fig.6 Typhoon speed at point 2 and 9
3.3.2 风向模拟
基于提出的桥梁节点风向角确定方法,可获取台风经过桥梁整个时段的各个节点风向变化时程,限于篇幅,选取运交点G左侧节点第2点和右侧节点第9点进行分析。
由图7可知,运交点左侧和右侧节点的时变风偏角变化规律不同,主要表现在台风中心通过桥梁区域时段。运交点左侧节点时变风偏角在整个台风经过时段内随时间逐渐减小,在台风中心通过桥梁区域时减小迅速。运交点右侧节点风向角在台风中心经过时发生突变,风向角在节点经过台风中心区域时刻的前后两个阶段均呈增大趋势。
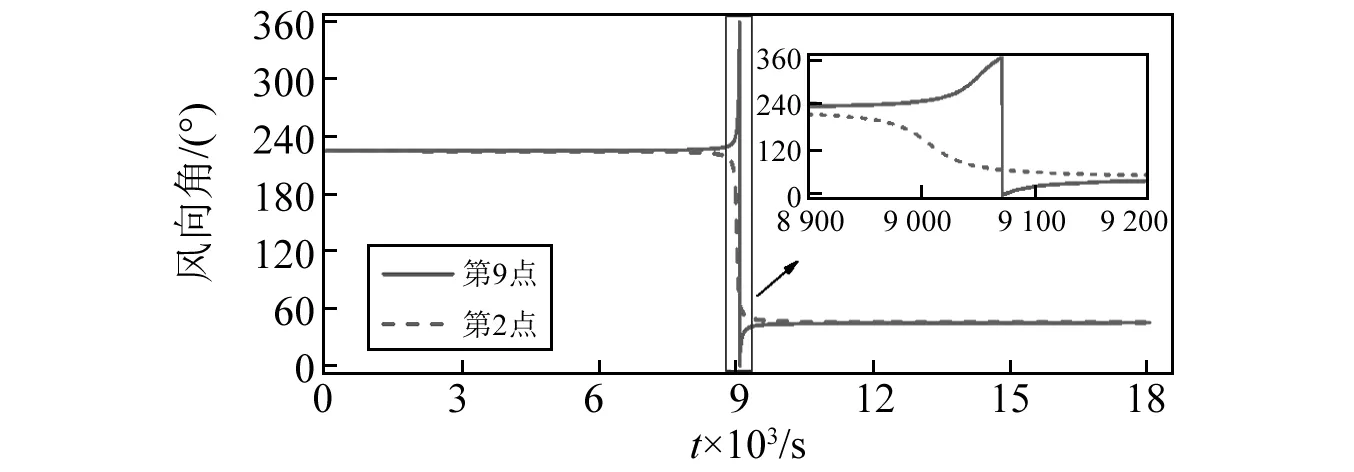
图7 第2和第9点的时变风向Fig.7 Time-varying wind direction at point 2 and 9
3.3.3 桥梁作用风速
在桥梁响应分析时,水平面上桥梁的作用风速为横桥向的风速分量。基于建立的风场模拟方法,在确定桥梁各节点风速时程和风向时程的基础上,求取横桥向风速分量,对桥梁作用风速进行分析。
在已有的桥梁风场模拟时,大部分研究仅对风场的风速进行模拟,对风向变化的考虑较少,在进行桥梁分析时,风来流方向集中于桥梁一侧。由图8可知,在整个台风时段内,第一阶段,风来流方向集中在桥梁一侧变化,第四阶段,风来流方向集中在桥梁另一侧。第二、第三阶段为风来流方向由一侧变换至另一侧阶段,定义为“异风向阶段”。在台风经过时,风来流方向由桥梁一侧变化至另一侧,且桥梁风向在时时变化,与以往的桥梁分析时单侧定风向的风场假定有根本性差异,会对桥梁的响应、疲劳等结果产生影响。尤其是在异风向阶段,桥梁各节点会依次出现风来流方向由主梁一侧变换至另一侧,在这个过程中,桥梁受圆心移动的逆时针环流风向作用,会对桥梁响应尤其是扭转响应产生影响,虽然风速较小,但需进行特别关注。
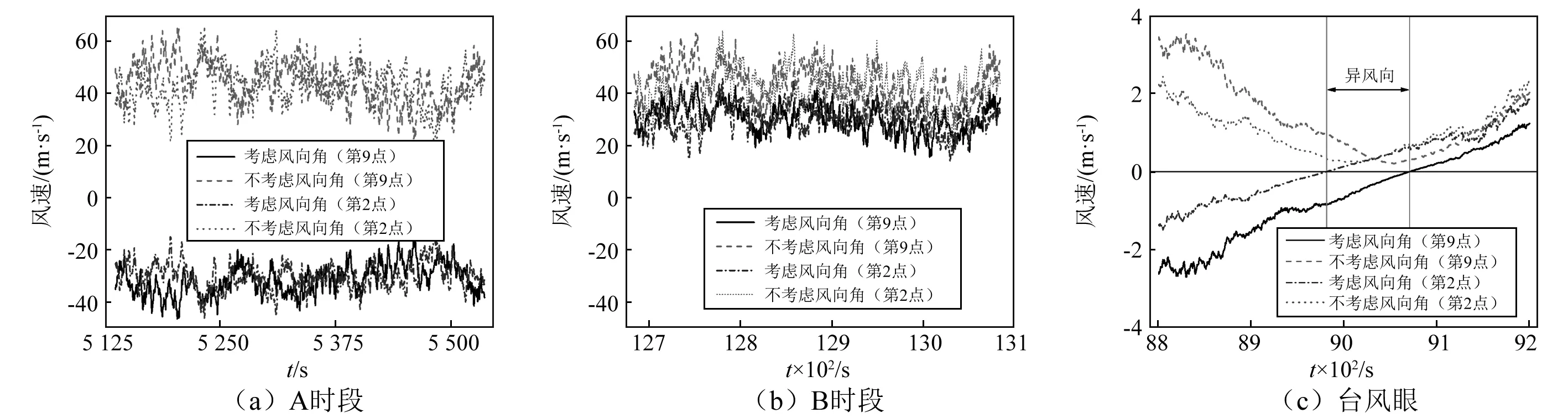
图8 第2、第9点考虑和不考虑风偏角风速对比Fig.8 Comparison of speed atpoint 2 and 9 considering and not considering wind yaw angle
4 结 论
(1)首次构建了大跨桥梁全过程台风三维风场系统模拟方法。该系统方法可考虑台风非平稳特性、时变风向、台风衰减、风剖面及桥梁各节点风速的空间相关性等,为大跨桥梁台风风场模拟提供有效途径。
(2)台风经过桥梁时,桥梁各节点的风向不同,且均具有时变性,导致桥梁各节点风速横桥向分量不同且均具有时变性,台风作用下的桥梁响应进行分析时,风向须纳入考虑。
(3)台风中心区域经过桥梁时,桥梁受圆心移动的逆时针环流风向作用,会对桥梁响应尤其是扭转响应产生影响,虽然风速较小,但环流风效应须特别关注。
(4)台风经过桥梁时段,风作用方向整体会由桥梁一侧变化至桥梁另一侧,这对桥梁响应、疲劳等的影响须引起关注。
(5)文中对台风登陆后运动规律做了服从匀速直线运动的假设,后期将对台风登陆后的运动规律进行研究并融入至风场模拟方法中。
