火炮后效期内弹底压力预估理论模型研究

周梦笛， 曹从咏， 钱林方

(1.南京理工大学 自动化学院， 江苏 南京 210094； 2.南京理工大学 机械工程学院， 江苏 南京 210094)

0 引言

在火炮射击过程中，弹丸运动经历内弹道、中间弹道(后效期)和外弹道3个阶段。在后效期，弹丸穿越火炮膛口流场时继续受到火药燃气的作用，将对弹丸受力及运动规律产生影响，这种影响包括弹丸获得的增速及受到的扰动[1]。

针对后效期的弹道研究兴起于第二次世界大战结束时，早期研究主要针对膛口流场，采用理论方法和各种实验方法进行气流特征和机理的分析[2-4]。Erdos等[4]根据二维定常射流理论，利用激波装配法建立了后效期冲击波波面和马赫盘的数值计算模型，该模型未考虑弹丸和膛口之间的相互作用以及弹丸对流场的影响，具有一定的局限性。随着计算机性能的大幅度提高，数值仿真发展迅速，国内外学者开始采用计算流体力学(CFD)方法对后效期流场进行仿真研究。苏晓鹏等[5]利用混合网格技术对带炮口装置的某火炮膛口流场进行了数值仿真，得到了弹丸出膛口后弹底合力的变化曲线。采用国际通用的大型流场仿真软件Fluent CFD，可以较精准地模拟后效期膛口流场及弹丸运动情况[6-8]，但CFD方法需要较长的计算时间，不适用于实际工程火控系统中。因此必须建立一种耗时小的快速计算模型方法，以预估弹丸弹底压力的波动情况。

根据已有研究可知，后效期内膛口附近的火药燃气流动主要是普朗特- 迈耶膨胀波及沿轴线的反射波起主导作用。本文采用完全不同于CFD的方法来模拟后效期弹底的压力变化，基于平面普朗特- 迈耶膨胀流动[9]，提出一种近似的中间弹道弹底压力半分析模型，以期迅速且较精确地给定外弹道的初始条件，从而为射表编制和弹丸合理设计提供理论参考依据。

1 后效期弹底压力预估理论模型

根据普朗特- 迈耶膨胀波关系及等熵流动，有下述关系：

uφ=c，

(1)

(2)

(3)

(4)

(5)

(6)

式中：uφ为流动速度u的切向分量；c为声速；ur为流动速度u的法向分量；Δh为比焓增量；um为炮口速度；φ为特征线倾角；φm为炮口马赫角；ρ为燃气密度；ρm为炮口燃气密度；cm为炮口声速；p为某一特征线对应的静压值；pm为炮口压力；Mm为炮口马赫数。炮口马赫角示意图如图1所示。

图1 炮口马赫角示意图Fig.1 Schematic diagram of Mach angle

将火药燃气看成是比热比为k的完全燃气，可以导出p与φ的关系式为

p=pm{cos[w2(φ-φm)]-

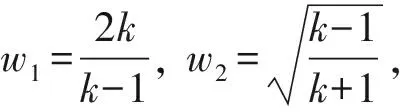
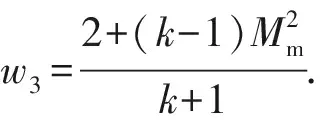
(7)

根据(7)式，可以算出倾角为φ的特征线到达弹底点处的静压值。为了求该点处的动压值，可利用流动速度的轴向分量ux，即

(8)

利用(9)式计算动压Δp的近似值：

(9)

在(9)式中，将弹丸速度近似处理为um，主要是考虑到在后效期内弹丸速度增加不多[10]，则将p+Δp看成是倾角为φ的特征线到达弹丸底部的作用力。由于该近似处理并没有考虑反射波达到该点处的作用力，需要综合考虑入射马赫波和反射波的共同作用，近似认为是两种波的叠加，为了考虑反射波的影响，采用声学近似方法处理。

根据图2所示的对称平面反射波性质，对于一给定的特征线，反射波压力和轴向速度相同，径向速度分量大小相等、符号相反，因此可以用(7)式、(8)式和(9)式计算反射波静压pr、反射波轴向速度uxr和反射波动压Δpr，即

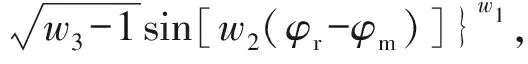
(10)

(11)

uxr=

(12)

式中：φr为反射波倾角。

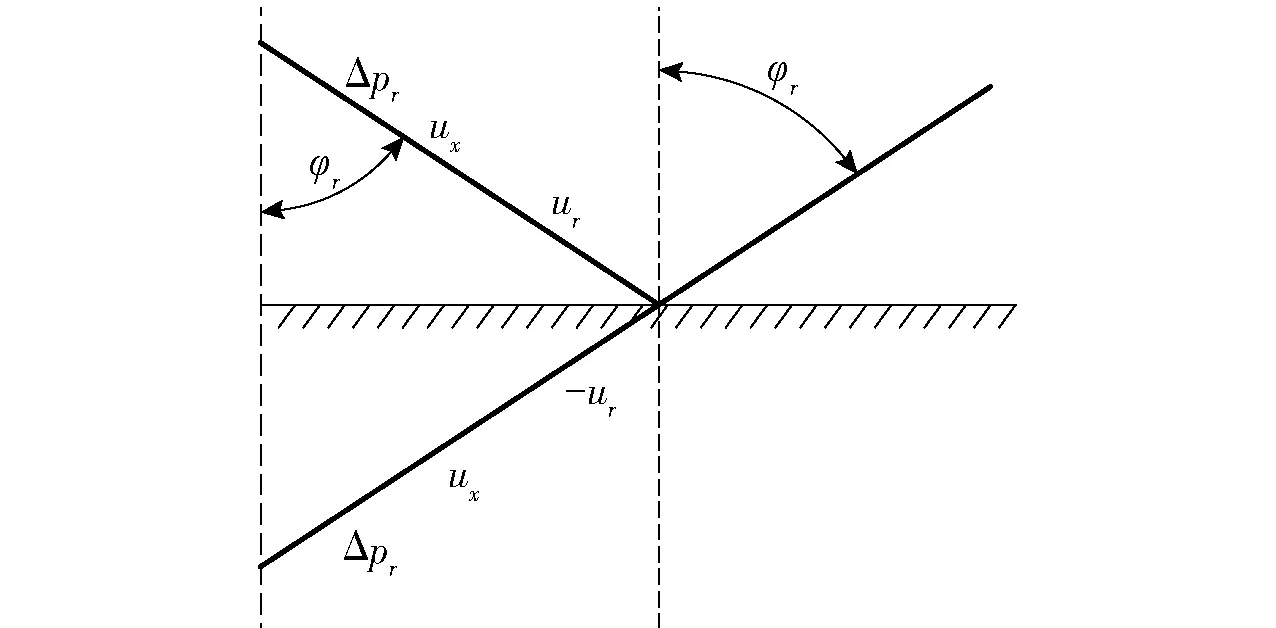
图2 对称平面反射波性质示意图Fig.2 Property of reflected wave on symmetry plane

然后进行平均压力的预估，如图3所示，对给定的弹丸运动位置x(t)，沿径向均分为n等分，节点数i为1，2，…，n+1. 则任意点的径向坐标为ri=rm(i-1)/n. 对每一点而言，若假定特征线为直线，则特征线入射波和反射波的倾角由(13)式和(14)式求出：

(13)

(14)

图3 弹丸底部径向分割示意图Fig.3 Schematic diagram of radial segmenting

对于给定的φ，由(7)式和(9)式计算p和Δp；对于给定的φr，由(10)式和(11)式计算pr和Δpr. 假定波的干涉呈线性，则第i个节点的合压力pi为

pi=p+pr-pm+Δp+Δpr，

(15)

进而有作用于弹底的平均压力为

(16)

2 弹底压力预估值边界估计

2.1 上界预估

第1节模型中仅考虑了平面对称性，没有考虑实际的圆柱轴对称流动问题。在轴对称模型中，普朗特- 迈耶流动的压力下降要比平面对称快得多，因此应该在近似模型中考虑弹底压力的上界预估。本文采用近似方法考虑轴对称问题，连续性方程为

(17)

式中：t为后效期时间；r为径向坐标。

对于等熵流动，p可由ρ计算得到，有如下性质：

p=p(ρ)，

(18)

(19)

(20)

将(18)式、(19)式和(20)式代入(17)式中，则(17)式为

(21)

式中：右端第1个和项表示平面对称流动的压力偏导数项。因此，沿着弹丸轨迹对(21)式进行积分，得

(22)

式中：τ为时间微元；Δpp为弹底动压，右端的积分项可以处理成平面对称流动的解的修正项，从而可以用前述方法计算Δpp并进行修正，该积分项可以通过连续时间间隔内的pi和uri求出。对于平面对称流动，径向速度分量ur预估值ur(φ)为

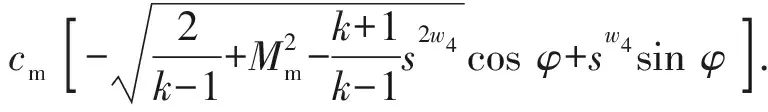
(23)

如果入射波与反射波存在相互作用，则ur可由(24)式计算：

ur=ur(φ)-ur(φr).

(24)

2.2 下界预估

与2.1节同样，通过近似处理方法也可以得到压力预估值的下界。由于将特征线处理成直线，造成所给出的特征线到达弹尾的时间早于实际特征线(见图4)，导致直线特征线比实际特征线的压力下降更快。在这种情况下，在后效期开始时刻，火药燃气速度为亚音速时需要采用基于一些修正的近似模型。此时，膨胀波进入炮口、导致燃气加速，使炮口处的流动变为音速流。这意味着普朗特- 迈耶流的第1条特征线位于炮口处，因此可以用第1节中的近似模型计算作用于弹体尾部的平均压力。前提是需要已知炮口处新的流动参数，这些参数不同于内弹道计算结果，为此本文提出如下近似方法。

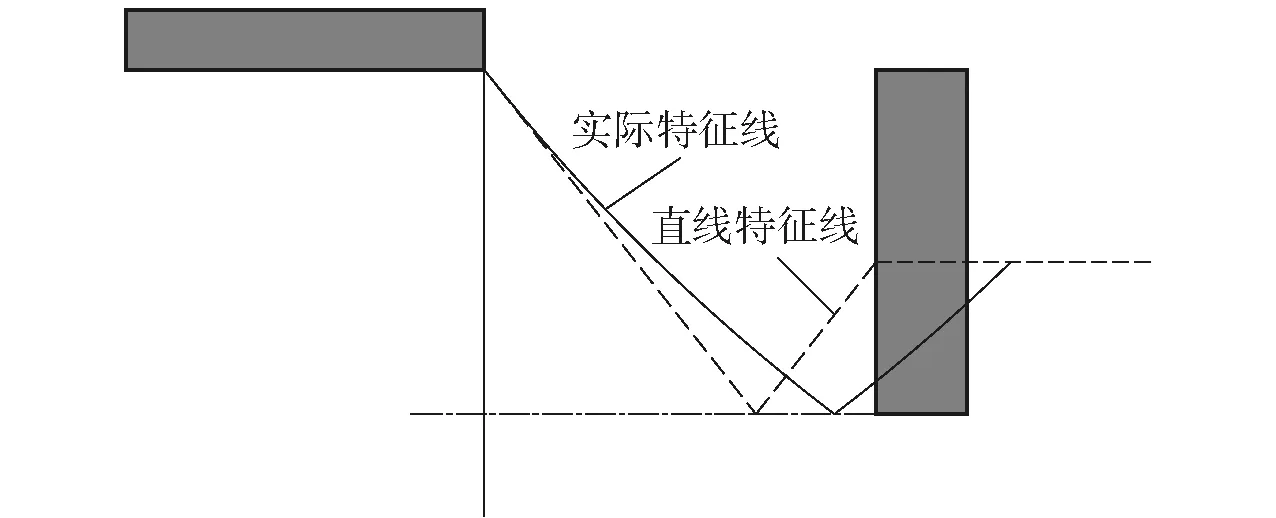
图4 直线特征线与实际特征线关系示意图Fig.4 Relationship between linear and real characteristic lines

如图5所示，假定在初始时刻中心膨胀波扇在炮管内产生，则可以通过中心膨胀波关系计算炮口处的速度和压力。

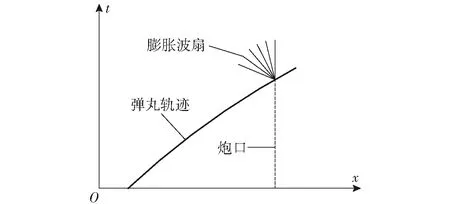
图5 初始时刻膨胀波扇示意图Fig.5 Schematic diagram of initial expansion wave

沿炮口处特征线，黎曼不变量关系式为

(25)

式中：u0、c0为内弹道终止时刻的流动速度和声速。

由于在炮口处um=cm，代入(25)式，得

(26)

(27)

本文认为火药燃气是完全燃气，利用等熵关系计算炮口处其他参量，并消去压力项，得

(28)

(29)

Mm=1.

(30)

3 仿真对比分析

以口径155 m某型火炮实弹射击试验中测得的膛口数据为例，将本文模型的计算结果与CFD三维仿真结果进行对比。

3.1 仿真参数设置

实弹射击试验测得3种不同出膛速度工况的后效期初始时刻膛口参数如表1所示，模型所需初始条件中的参数pm、ρm、um取表1中的数据，k取1.3，rm取0.077 5，用MATLAB编程实现本文模型的计算。

表1 计算工况表

CFD仿真时设置计算域为10 m×5 m×5 m的长方体，计算网格数约为110万。根据经典内弹道理论，假设膛口压力、温度、密度随时间呈指数衰减规律[11-12]，并编写用户自定义函数(UDF)实现膛口火药燃气的排空过程，采用密度基瞬态求解器进行求解。

3.2 对比分析

考虑到CFD仿真耗时较长，本文仅对距离膛口20 cm内弹底压力的波动情况进行仿真，所得结果如图6以及表2～表4所示。由如图6以及表2～表4可以看出：不同工况下本文模型计算得到的弹底压力曲线与CFD三维仿真结果都较接近，表明本文模型与CFD模型仿真结果相差很小；每个工况本文模型的计算耗时不到1 s，CFD计算耗时约1.5 h左右，表明本文模型计算耗时比CFD模型显著减小。

图6 弹底压力变化曲线图Fig.6 Curves of pressure on the bottom of projectile

表2 工况1下CFD模型与本文模型计算结果对比

Tab.2 Comparison of calculated results of CFD model and the proposed model in Case 1

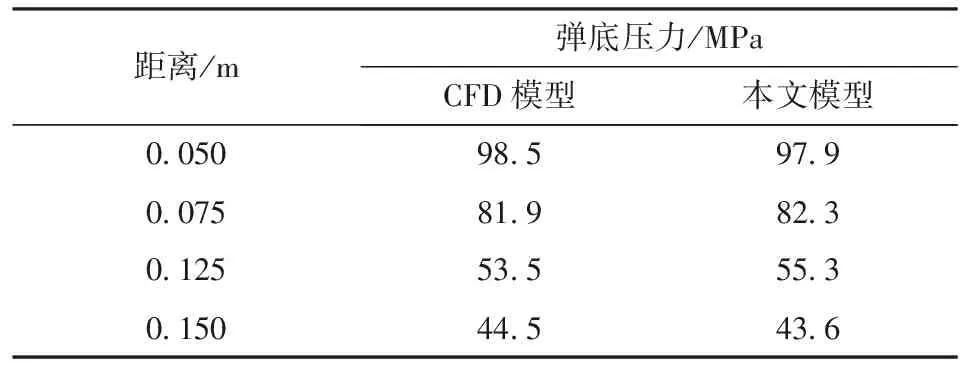
距离/m弹底压力/MPaCFD模型本文模型0.05098.597.90.07581.982.30.12553.555.30.15044.543.6

表3 工况2下CFD模型与本文模型计算结果对比

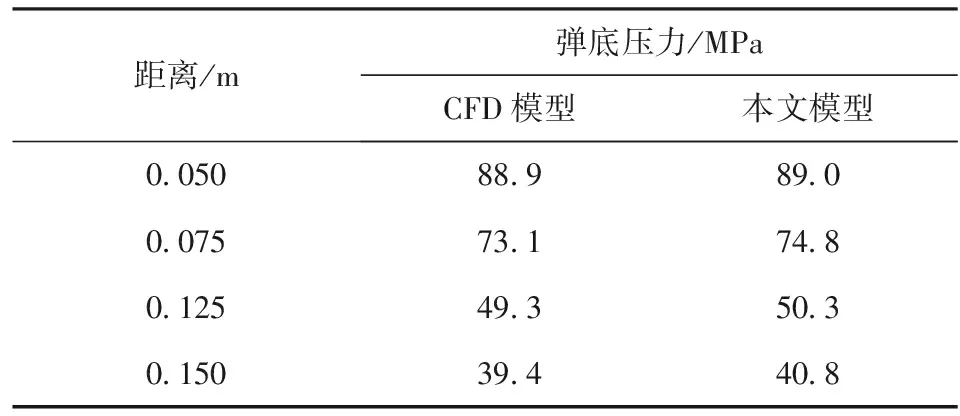
表4 工况3下CFD模型与本文模型计算结果对比

4 结论

本文对后效期弹底压力的波动进行了研究，基于普朗特- 迈耶膨胀波和等熵流动，建立了后效期弹底压力预估理论模型。以某弹丸为例，将该模型计算结果与常用的CFD三维仿真模型计算结果进行了算例对比。结果表明：本文提出的弹底压力预估分析模型能够合理地反映后效期弹底压力的变化规律，所采用的数值计算方法与CFD方法相比计算精度相当，但计算耗时显著减少。本文研究成果可为火控系统所需外弹道参数提供一种快速的计算方法，并可为射表编制和弹丸合理设计提供理论参考依据。