弹载探测器自适应高分辨前视成像策略研究

程呈， 高敏， 周晓东， 李超旺， 于波， 刘永鹏

(1.陆军工程大学石家庄校区 导弹工程系， 河北 石家庄 050003；2.陆军工程大学石家庄校区 弹药工程系， 河北 石家庄 050003；3.北方自动控制技术研究所， 山西 太原 030006)

0 引言

新型箱式远程火箭弹需要根据预设任务要求，在不同炸高条件下执行不同的作战任务[1-2]。新型火箭弹上搭载了炸高可选择近炸引信，通过弹载相控阵探测器对弹药前视区域地表进行探测，可以获得高分辨的前视图像，从而保证其能够顺利完成预设高度下的作战任务。

前视成像技术研究已经开展多年，相关研究成果层出不穷，主要集中于合成孔径雷达(SAR)成像技术、实波束扫描成像技术与单脉冲成像技术三方面。温晓杨等[3]根据相控阵原理设计了同时多波束天线方向图，推导了方向图各波束指向、波束宽度与阵列结构相关参数的关系；在对回波信号特性分析基础上，利用方位向上的非线性调频变标算法分别进行SAR成像。周松等[4]针对俯冲下降阶段的弹载SAR成像问题，建立了调频连续波(FMCW)-SAR回波模型，通过在二维频域构造相应的剩余二次相位补偿函数，较好地改善了弹载距离向的聚焦质量和成像效果，该算法运算效率较高，适用于弹载平台。周鹏等[5]提出了一种新的弹载SAR成像方法，将目标斜距方程近似为慢时间的4阶近似式，再利用卡尔丹方程解算获得驻相点的精确解，从而获得信号的二维频谱表达式，进而获取前视距离像。

弹载SAR成像技术因其固有的成像特点，只能成斜前视或侧视图像，并且前视SAR成像时需要对探测器本身的航迹提出严格要求，与本文所涉及的背景不符。ZHANG等[6]建立了机载前视扫描成像模型，同时优化了目标与传感器之间的距离向解算方程，并通过反解混合矩阵得到探测范围内的目标距离像，该方法的重点在于反解混合矩阵是一个欠定条件下的矩阵估计问题，因此天线阵列的规模成为制约估计精度的重要因素，规模越大，估计精度越高。YANG等[7]针对地杂波环境下的前视多输入多输出(MIMO)雷达成像问题，提出基于压缩感知的成像方法，主要解决了不同环境下的成像，通过设置自适应参数实现不同杂波环境下的稳定成像。温晓杨等[8]提出了一种基于实波束扫描的相控阵雷达前视成像方法，对当前广泛研究的解卷积前视成像方法的优势和劣势进行了深入分析，指出未能有效提高方位分辨力的原因，并在此基础上提出了基于压缩感知理论的扫描雷达前视成像方法；通过对大时宽带宽积信号的脉冲压缩获得径向高分辨，并基于场景中的强散射中心分布具有稀疏性(可压缩)这一事实，利用压缩感知最优化方法获得高的方位分辨力。CHEN等[9]利用单脉冲测角技术，有效提高了探测波束范围内的成像分辨率，通过简单仿真反映出该方案的可行性与有效性。OJOWU等[10]针对前视探地雷达(FLGPR)探地成像问题进行了研究，利用高稀疏迭代协方差估计(SPICE)对观测矩阵进行近似估计，通过多次迭代算法提高估计结果、保证方位向的分辨率，最终通过实验结果表明了方法的可行性与优越性。但是多重迭代算法导致成像周期较长，不利于弹载探测器的应用。实波束扫描前视成像的方位分辨率完全受限于发射波束宽度，为提高其分辨能力，探测器往往相对复杂，弹载平台很难为探测器提供较大的空间。

单脉冲成像技术将天线扫描与单脉冲测角技术相结合，利用高精度测角提升成像质量，现已应用于多种前视高分辨处理过程中。何松华等[11]针对弹载宽带相控阵单脉冲雷达体制以及强海杂波背景，提出了一种基于通道级空时自适应处理(STAP)技术与自适应发射波束形成(ATBF)的杂波已知、目标检测与角度测量方法，在实验测量过程中，有效提高了目标角度的测量精度和角度分辨率。吴迪等[12]针对单脉冲成像技术的实际处理问题，提出一种用于单脉冲成像的自聚焦算法，利用迭代方式自动从雷达接收数据中挑选孤立强散射点回波信号精确估计实际鉴角曲线，用于单脉冲成像，实现图像方位自聚焦，并通过仿真实验证明了该算法的鲁棒性与可行性。国外相关学者HENRY等[13]和HYUKJUNG等[14]利用单脉冲测角技术进行前视成像并运用于不同领域，利用神经网络提升了方位向角度识别的精度，使成像分辨率提升约为传统实波束扫描的8倍以上，运用到前视目标探测也取得了较好的效果。但其神经网络训练耗时较长，且整个网络的复杂程度较高，不利于弹载探测器。

单脉冲成像具备系统结构复杂度低、实时性强、对探测器航迹无特殊要求等优点，能够应用于弹载平台。基于此，本文针对弹载探测器前视对地成像问题，提出一种有效的前视高分辨成像策略。结合目标区域回波数据，自适应地优化鉴角曲线，利用单脉冲测角技术提高角度分辨率，使其满足高分辨成像要求；对相应角度下的目标区域纵向到达角DOA进行估计，解算得到目标区域内的高程信息。

1 问题描述

新一代箱式远程制导火箭弹搭载新型炸高可选择近炸引信，用于在末端(下降段)进行精确的载弹高程解算，满足作战任务需求。弹载探测器在预设测量区域开启工作，如图1所示。

图1 弹载探测器炸高测量示意图Fig.1 Burst height measurement by missile-borne detector

由图1可见，弹载探测器为平台式相控阵探测器，位于引信前端，并与弹轴垂直，信号处理电路位于其后。根据预设作战任务的要求，在下降端某处探测器开始工作，向弹丸速度的下视方向发射探测波束，对探测区域内的地面物体进行测量并成像。图1(b)显示了同一距离维的回波截获过程，由于图1(b)为示意图，距离方向上的弧度忽略不计。由图1还可以看出，在一定探测范围内，同一距离维的角度分辨率决定了最小分辨单元的宽度，即探测分辨率。

单脉冲成像具备系统结构复杂度低、实时性强、对载弹航迹无特殊要求等优点，能够用于弹载探测器前视成像过程。但在实际应用过程中，弹载探测器测量前视范围内的有效高程时，总会遇到某些特殊地形、地貌，例如高耸的尖峰、大幅的凹陷等。图2所示为根据高程地形图提取出的某一块地形，其海拔高度在200～1 400 m范围内，但是地形起伏较大。若载弹在此类地形上空飞行(探测区域如图中红色方形所示)，则传统的像测高方法势必会降低探测区域内地貌信息，导致测不准、打得偏。

图2 实际地貌示意图Fig.2 Actual terrain map

上述地形真实存在，并且会对弹载探测器测高带来巨大的测量误差。为避免上述情况，大幅度提升探测区域的角度分辨是高分辨前视成像研究的重点。

2 自适应高分辨方位向测角

结合单脉冲测角技术，对探测区域内同一距离维下的不同方位向单元实施自适应高分辨测角(AHR-AMA)。测角过程中，通常利用比相模式进行角度解算，令Σ(θ)、Δ(θ)分别表示和、差天线方向图，理想条件下，Σ(θ)、Δ(θ)的关系可以表示为

Δ(θ)=Σ(θ)·tan(kπθ)j，

(1)

式中：θ为目标偏离探测波束中心的角度；k为常数。因此，将tan(kπθ)视为和、差比的虚部，则θ可以表示为

(2)

式中：[]imag为取虚部函数。传统意义上的单脉冲测角，将探测范围内的全部回波数据用于形成和波束、差波束，从而进行角度解算，使方位向角度分辨率较低，难以实现高分辨测量。究其原因，是tan(kπθ)曲线的尖锐程度直接影响了角度分辨率。为此，寻找最优的鉴角曲线成为实现方位向高分辨测角的关键。

仅考虑方位向，设探测波束以角速度ωθ进行方位向扫描，且在t时刻发现波束覆盖范围内的点目标。由于雷达回波数据可视为目标表面散射系数与天线方向图的卷积，和波束、差波束可以表示为

(3)

式中：A为目标表面散射系数；θt为t时刻点目标与波束轴线夹角；r表示第r个距离维。则由目标回波数据之比得到实际鉴角曲线为

(4)

在探测过程中，最强散射点所反映的回波强度最大，当方位向测角分辨率达到最优时，该点处的回波响应应该无限趋于冲激响应函数。受此启发，将同一距离维下最强散射点相邻范围内的回波数据作为参考数据，设定评估阈值，通过不断迭代计算、修正并缩小相邻数据范围，从而获得最强散射点范围内的鉴角曲线，该曲线即是该距离维下的最优鉴角曲线。用该曲线数据进行同一距离维下的方位向测角，必然能够提升测角精度。AHR-AMA具体步骤可以归纳如下：

步骤1获取回波数据。

设回波经脉压后的和、差通道回波信号分别为Sum(r,t)、Diff(r,t)。进行方位向测角时，设测角结果中最大幅度对应的时间为tmax，则认为该时刻对应的是r距离维内的最大散射目标点。由于此时获得的目标角度信息应用的是(4)式所示的鉴角曲线，测量时间与实际对应时间存在误差，记为Δtmax.

步骤2设定数据范围。

取tmax相邻时间范围，记为Tn，其中n表示迭代次数，则Tn可以表示为

Tn={t|tmax-tδn≤t≤tmax+tδn}，

(5)

式中：tδn为第n次迭代时所取的时间范围，Tn的宽度为2tδn，且tδn的取值范围不超过天线扫过单个波束主瓣宽度的时间。则更新后的区域回波和波束、差波束可以表示为

(6)

式中：当n=1时，所得和波束、差波束数据称为初始数据。

步骤3解鉴角曲线。

每一次迭代时的方位向鉴角曲线可表示为

(7)

步骤4更新迭代条件。

最优的鉴角曲线在距离维最强散射点处呈现出类似冲激响应的图形，因此利用能量占比确定其是否达到最优。设最强散射点处的能量为P(r,Tn)，其他区域能量为Pr(r,Tn)，阈值为T(r)，则有

(8)

当且仅当H1事件(能量比大于或等于预设阈值)发生时，认为tanr(kπθ)是距离维r下的最优鉴角曲线；当H0事件(能量比小于预设阈值)发生时，需要更新时间范围tδn，并进行第n+1次迭代。迭代的约束条件应该以满足预设分辨率为宜，过多追求分辨率精度会导致冗余计算。因此增加约束条件，当tδn/tδ1≤λ时(λ为预设分辨率)，即可停止迭代计算，并认为此时鉴角曲线最优、迭代次数最少。

步骤5修正中心位置。

(9)

在进入下一次迭代计算时，需要修正最强散射点回波的中心时间，利用tmax,r代替tmax，进行新一轮迭代计算。

步骤6测量方位角度。

设经迭代计算，距离维r下的最优鉴角曲线为tanr(koπθ)，其中ko表示最优k值。利用tanr(koπθ)对距离维r内的目标散射点进行角度估计以及幅度和相位检测。获取该距离内的所有目标角度集合θr后，即可根据(r,θr)确定目标位置，为后续的载弹高程解算提供支持。

3 载弹高程解算策略

载弹高程解算基于确定目标位置后进行，利用弹载探测器俯仰差通道的回波数据进行角度估计，从而获取载弹高程信息。弹载探测器的高频波导口定义如图3所示。

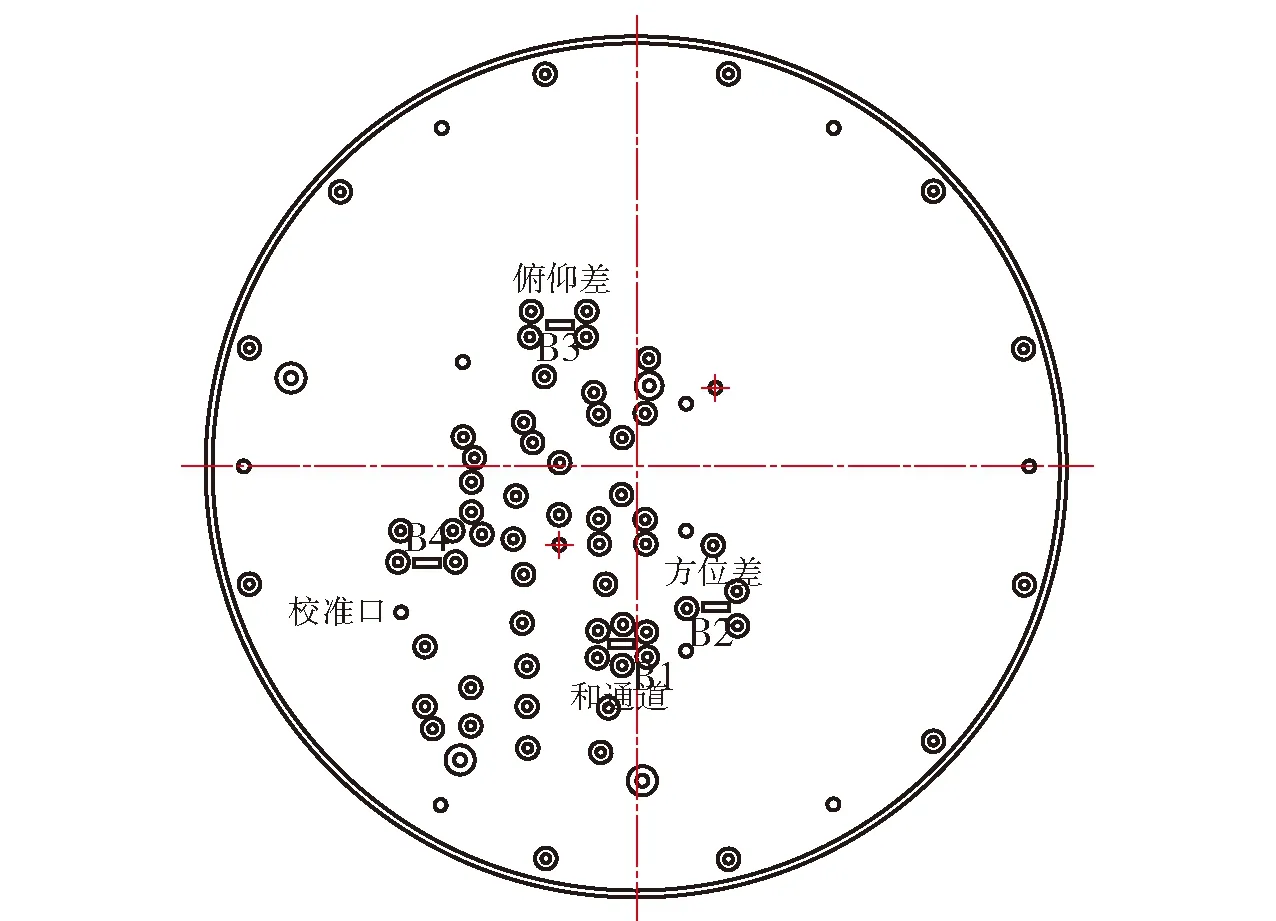
图3 高频波导口定义示意图Fig.3 Schematic diagram of high frequency waveguides

收发信道(射频前端)由1个收发共用通道、3个接收通道和1个校准通道组成。其中，发射通道包括上变频模块、功率放大器、环行器等，中频激励信号经发射通道变频放大，由天线辐射出去。天线接收目标信号，并经3个单通道接收模块输出中频信号，其中和通道接收与发射通道共用环行器前端部分，其他方位差和俯仰差通道的接收模块与和通道组成一致。

设(r,θr)处存在目标，目标高度为Ht，弹载探测器高度为Hd，探测波束经过目标反射后所成角度为β. 对θr单元进行切片处理，得到载弹高程解算模型如图4所示。

图4 弹载探测器对(r,θr)目标测高模型Fig.4 Height measurement model of missile-borne detector for (r,θr) target

以(r,θr)的高度目标为例，设发射信号为S(r,θr)，目标直接回波为Sd(r,θr)，二次回波为St(r,θr)，则

(10)

式中：f1为直接回波角度函数；f2为二次回波角度函数；K1为直接回波幅度参数；K2为二次回波幅度参数；g为时间延迟函数；τs-d为探测波束与直接回波之间的时间延迟；τd-t为直接回波与二次回波之间的时间延迟。

利用单脉冲测角技术，对θr方向的回波信号进行角度估计。但是由于探测目标基本为地面低矮物体，距离地面较近，二次回波信号受地杂波影响较大，在单脉冲测角过程中会出现严重的角闪烁现象，仅能够从回波中准确获得直接回波到达角κDOA，对于二次甚至更高次回波数据角度估计会产生较大的误差。

如图4所示，由于弹载探测器的飞行高度相对于地面目标为较大值，a、b、c向量之间的关系为

当Hd≫Ht时，
有|a|≈|c|,|b|≈Ht，

(11)

且认为β很小，则造成二次回波与直接回波之间时间延迟的波程差仅为|b|，因此可得

(12)

式中：c为电磁波传播速度。由此可见，上述两回波之间时间间隔的获取显得尤为重要，获得的时间延迟精确程度也会制约载弹自身高程解算能力。

综上所述，可得整体的前视成像策略流程如图5所示。

图5 探测区域成像流程Fig.5 Flow chart of forward-looking imaging strategy in the detection zone

由图5可知，本文提出的高分辨前视成像流程可分为3个阶段：

1)获取目标初始回波数据。弹载探测器截获得到目标回波信号后，将方位差通道、俯仰差通道以及和通道中的信号数据进行数据筛选。

2)迭代获取最优鉴角曲线。主要通过第2节所述算法，首先经过回波数据估计得到每一距离维上的强散射点；然后求解同一距离维的最优鉴角曲线，若符合判别要求即停止计算，则认为此时求解得到的鉴角曲线为此距离维内最优，若不符合判别要求，则需更新迭代参数、数据范围，同时修正中心位置，重新求解鉴角曲线，直至符合判别条件。

3)求解目标区域信息并成像。根据上述步骤获取探测区域目标区域的角度信息，同时利用本节的载弹高程测量模型，对载弹高程进行解算，最终将角度与高度数据通过数据融合处理得到前视探测区域成像。

该策略可在鉴角曲线完全未知情况下仅由回波数据自适应估计，并不断迭代形成距离维内的最优鉴角曲线，实现前视高分辨单脉冲成像，且对不同数据具备较强的鲁棒性，能够适用于弹载平台。

4 仿真实验和测试试验验证

为验证本文所提前视高分辨成目标像策略的可行性与优越性，进行一系列仿真实验与实测试验。

4.1 仿真实验1：鉴角曲线误差影响单一目标成像

由第2节所述，鉴角曲线tan(kπθ)对于方位向的测角会产生较大的影响。仿真过程中，设发射方向图半波宽度为1 rad，目标偏移中轴线0.3 rad，地面散射系数为1. 和波束、差波束方向图如图6所示。

图6 和波束、差波束方向图Fig.6 Patterns of sum beam and difference beam

为分析鉴角曲线的精确程度与最终目标方位向角度分辨率的关系，将探测前提简化。设探测波束静止(无方位向运动)，利用单脉冲测角技术，得出不同k值条件下的鉴角曲线与理想鉴角曲线对比结果，如图7所示。对单一目标进行成像的结果如图8所示。

图7 不同k值条件下鉴角曲线与理想鉴角曲线对比Fig.7 Comparison among different resolution angle curves in different k and ideal resolution angle curve

图8 不同k值条件下角分辨结果Fig.8 Angle-distinguished result under different k conditions

由图8可以看出，不同鉴角曲线确实会影响最终方位向角度的分辨结果，主要体现在对于角度分辨的聚焦程度方面。更优的鉴角曲线呈现出更接近冲激响应的测角结果，与第3节理论推导结果相符，因此在实际的成像过程中，鉴角曲线的准确程度势必会影响最终的成像结果。

4.2 仿真实验2：高分辨方位向成像

将本文成像策略与传统实波束扫描成像算法进行对比，以体现本文成像策略的优越性。

与理论推导有所不同，为满足弹载毫米波探测器的成像精度要求(≯2.5 m)，在仿真过程中，将(7)式、(8)式推广到一般情况，则有

(13)

(14)

其中：(13)式用于求解r至r+n距离维内的最优鉴角曲线，(14)式表示tanr,r+n,o(kπθ)的判决条件。利用每一距离维内的最优鉴角曲线均值确定迭代停止次数，仿真参数如表1所示。

分别利用两种不同的成像策略对前视目标进行成像，得到的成像结果如图9所示。

表1 仿真参数

图9 两种成像算法的成像结果Fig.9 Imaging results of two imaging algorithms

由图9中的方框放大部分可以看出，两种成像算法得到的成像结果分辨率有较大区别，本文所提策略具有更优的角度分辨率。成像中心的方位剖面如图10所示。

图10 单脉冲成像中心点方位剖面图Fig.10 Azimuth profile of the center of monopulse imaging

由图10可以看出，本文单脉冲前视成像策略能够大幅度提升方位向分辨率，且成像品质更加优越，可满足弹载探测器高分辨成像的要求。

4.3 测试试验3：利用实测方向图数据进行高分辨成像精度分析

图11 现场环境及测试过程Fig.11 Test environment and process

测试的暗室环境如图11(a)所示，其方位、俯仰方向图在紧缩场暗室中测试，方向图测试现场如图11(b)所示，探测器收发天线测试现场如图11(c)所示。

利用暗室得到的和通道、方位差通道和俯仰差通道的方向图结果如图12所示。

图12 不同探测角度下和通道、差通道实测结果Fig.12 Actual test results of sum and difference channelsat different test angles

通过不断缩小数据范围，最终得到同一距离维下角度分辨率的变化如图13所示。

由图13可见，随着迭代次数的增加，同一距离维下的角度分辨能力得到了有效提高，反映出本文提出高分辨成像策略的有效性。迭代的精度可根据不同作战任务的需要进行改变，从而使引信能够利用回波数据自适应地提升方位向测角精度，测角精度一旦提升，即能实现探测区域的高分辨成像。

5 结论

针对新型远程制导火箭弹的作战任务需求，本文提出一种弹载探测器的自适应高分辨前视成像策略；通过三通道回波数据的迭代与优化，不断提升方位向的角度分辨能力，进而利用单脉冲成像技术对前视探测区域进行成像。所得主要结论如下：

1) 本文所提策略相对于传统实波束扫描成像技术，在成像精度方面有了明显提升。

2) 提升的方位向分辨率约为传统实波束扫描成像算法的10倍，算法复杂度较低，在迭代到第8次时即可达到预设的分辨率要求。

3) 单脉冲成像模块具备系统结构复杂度低、实时性强、对探测器航迹无特殊要求等优点，能够应用于弹载平台，具有一定的军事应用前景。

本文策略存在的问题主要是算法对于迭代次数的控制，下一步主要将重点集中于阈值函数((8)式)的优化，以确保迭代过程中不会出现冗余迭代计算。