2,4-二硝基苯甲醚基熔铸炸药慢速烤燃过程传热特征分析

2019-08-06周捷智小琦刘子德王雪王帅

兵工学报 2019年6期

周捷，智小琦，刘子德，王雪，王帅

(中北大学机电工程学院，山西太原 030051)

0 引言

2,4-二硝基苯甲醚(DNAN)作为炸药，最早出现于第二次世界大战时期，其密度与能量均低于梯恩梯(TNT)，仅被作为TNT的廉价替代品。20世纪下半叶，西方国家发现DNAN比TNT具有更低的感度与毒性，且能与高氯酸铵(AP)相容，改善氧平衡，弥补其能量不足的缺点[1-2]。美国于1960年首先研制出一系列以DNAN为载体的塑性钝感炸药并投入生产[3]，近些年来国内关于DNAN的研究也从未间断。高杰等[4]研究发现，当铝粉质量分数小于20%时，适量添加铝粉能显著提高DNAN基复合炸药的爆轰威力。王春光等[5]认为合理的配方再加上适当的装药工艺，能使DNAN熔铸炸药的能量达到2倍TNT当量。罗一鸣等[6]和蒙君煚等[7]分别研究了DNAN单质与混合炸药的凝固特性，发现DNAN的凝固收缩率虽略高于TNT，但通过优化铸药工艺能有效地减少炸药的内部疵病。王红星等[8]和陈朗等[9]先后都对DNAN的烤燃特性做了研究，分析了DNAN单质炸药的热刺激响应特征。目前很少看到国内关于DNAN基混合熔铸炸药热刺激响应特征分析方面的报道。

相变炸药在热刺激下的内部变化过程完全不同于非相变炸药。药柱在受热时发生相变，非均匀温度场中液态炸药在浮升力驱动下形成自然对流，对流的存在使相变炸药与非相变炸药的温度场分布有明显区别，导致点火响应区域和响应等级有很大差异[10]。

为了研究相变炸药的传热特征，本文以DNAN基熔铸炸药为对象，通过实际烤燃试验结合数值模拟，分析整个烤燃过程中炸药内部的温度变化与质量流动，得出影响其响应特征的因素，以期为DNAN熔铸炸药的工程应用与热刺激防护提供参考。

1 烤燃试验

1.1 试验准备

采用传统方法进行慢速烤燃试验，烤燃系统如图1所示，该系统主要分为炉体、烤燃弹与日本岛电公司生产的MR13温控仪3大部分，通过普通K型热电偶将弹体外壁的温度反馈到温控仪内，温控仪将反馈回的数据与设定值对比，利用比例- 积分- 微分(PID)控制算法自动控制加热炉内的功率，保证升温速率稳定，温度误差小于0.5 ℃.

图1 烤燃系统示意图Fig.1 Schematic diagram of cook-off system

为了尽量减小热电偶探针对相变后炸药内部对流场的影响，选用微型热电偶。将热电偶探针固定在弹体内，然后注入炸药冷却成型，从而避免接触热阻对烤燃前期热传导的影响，也更接近铸装药战斗部的真实内部情况。

壳体材料选用45号钢，壁厚3 mm，上下端盖厚1 mm，内装DNAN基熔铸炸药(31.6%DNAN、41%黑索今、25%铝粉、2.4%添加剂)，密度1.8 g/cm3. 药柱尺寸为φ19 mm×38 mm. 在药柱内部预设2个测点，A点在药柱的几何中心，B点在水平方向偏离几何中心6 mm处，W点为弹体壁面温度测点，如图2所示。

图2 烤燃弹布置Fig.2 Cook-off bomb layout

将普通K型热电偶固定在烤燃弹外壁后，将弹体竖直吊放到炉体中央，如图3所示。

图3 烤燃弹试验状态图Fig.3 Ready for test

1.2 试验方案

采用上述方法对3发弹体进行慢速烤燃试验。弹体在烤燃炉内以1 K/min速率从室温开始加热，MR13温控仪以1 s为采样周期记录每个通道的实时温度数据，直至发生响应。待炉内温度冷却至室温后，回收弹体并观察分析。

1.3 试验结果及分析

响应后回收的弹体如图4所示。

图4 响应后回收的弹体Fig.4 Bombs after ignition

观察回收的弹体发现：3发弹体外形均大致完整，并未发生太大的形变，端盖发生剪切破坏并与弹体分离。第1发弹体上下端盖均发生了剪切破坏，上部端盖有大量黑色糊状物与少量白色炸药残留物，下部端盖有大量炸药残留物，未发现有燃烧痕迹；第2发弹体两端盖均脱离弹体，且上部端盖螺纹连接段发生了剪切破坏，下端盖螺纹段完整；第3发弹体仅上端盖被破坏，下端盖出现突起但未被破坏。

综合3发回收弹体的外形变化判断，尺寸为φ19 mm×38 mm的DNAN基熔铸炸药药柱在1 K/min热刺激作用下最终均发生燃烧反应，且上半部反应程度更为剧烈。

3发试验获得的响应温度曲线大致相同，取第1发试验中测点的温度曲线进行分析，结果如图5所示。

图5 测点温度变化曲线Fig.5 Temperature curves of measuring points

由图5可以清晰地看出：升温开始后，炸药内部2个测点的温度曲线经过一个短暂的温度滞后过程，然后达到与外壁一致的升温速率；当温度升至73 ℃左右时，炸药内两测点的升温速率开始减慢，出现一个明显的吸热过程，表明此时炸药已开始熔化；当外壁温度升至80 ℃左右时，两测点的升温速率同时开始加快，表明此时炸药已完全熔化为液态；当外壁温度升至175 ℃左右时，由于炸药分解产生的热积累效应开始加剧，炸药内部温度快速上升；当外壁温度升至193.5 ℃时，炸药内部的温度高于外壁，受其影响外壁温度上升速率加快；当炸药内部温度升至205 ℃左右时，3个测点的温度曲线同时出现阶跃，此时炸药发生了响应。

通过以上分析可知，试验所用DNAN基熔铸炸药的相变温度约为73 ℃，低于DNAN单质炸药的相变温度[9]，相变时间持续约8 min，实际响应温度约为205 ℃.

图6为整个烤燃过程中壁面温度与测点A的差值曲线。从图6可知，当炸药内部升温速率开始稳定至炸药发生相变前这段时间内，壁面温度与测点A的温差基本稳定。相变开始阶段温差急剧增大，相变结束后温差先减小、后小幅增大，然后急剧减小，最后趋于稳定直至响应，温差总体趋势趋于减小。McClelland等[11]曾在B炸药的烤燃试验中也观察到了类似的现象，但未做出解释。

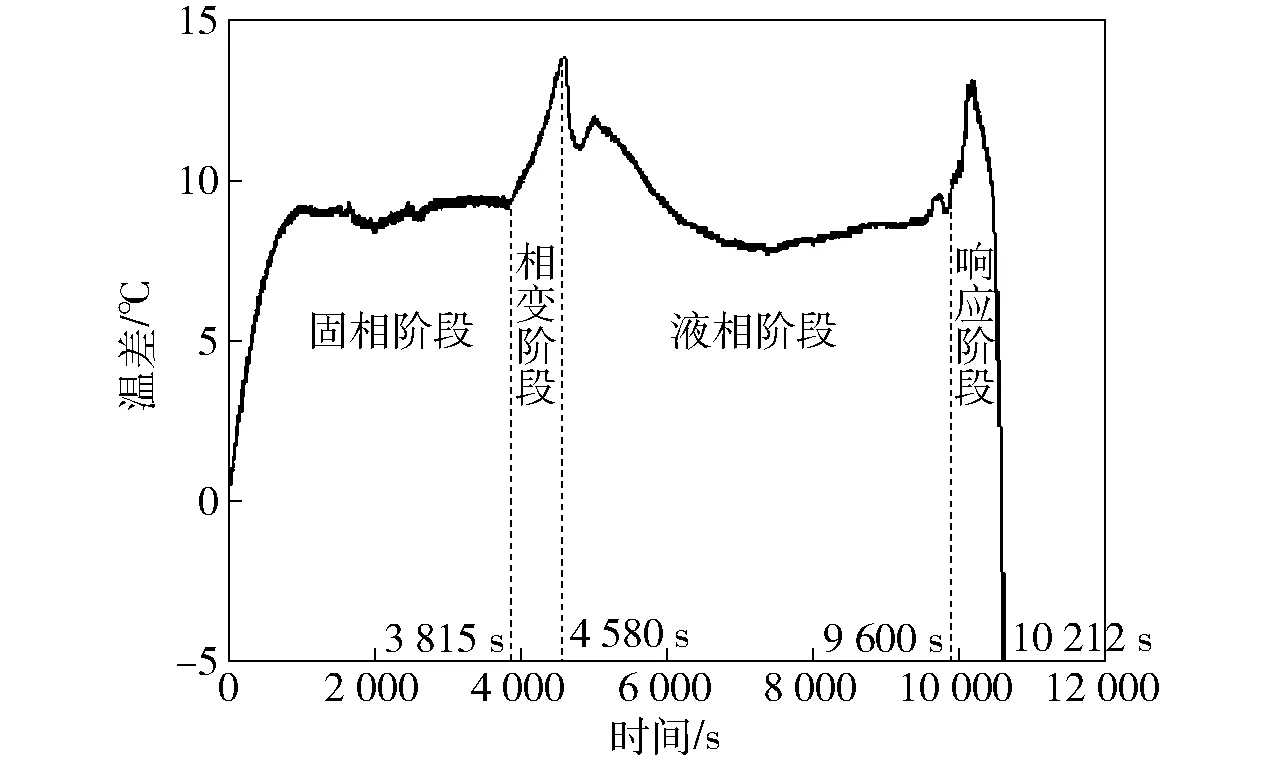
图6 壁面与测点A的温差曲线Fig.6 Temperature difference of wall and measuring point A

升温开始后，炸药外部温度升高，但由于炸药是热的不良导体，热量无法迅速传递到炸药中心，导致外壁和中心的温差开始增大；当热量传递到炸药中心后，温差逐渐稳定。

当温度升至炸药的熔点时，靠近外壁的炸药首先开始发生相变；相变是一个吸热过程，导致外壁与中心的温差再一次增大，直至相变结束。

相变结束后，炸药内部的传热方式有辐射、热传导与对流传热，瑞利数Ra是描述对流传热强度的无量纲数[12],具体表达式为

(1)

式中：Pr为普朗特数；Gr为格拉晓夫数；ν为运动黏度；α为热扩散系数；g为重力加速度；β为体积膨胀系数；L为特征长度；ΔT为对流两端温差。试验中这些参量只有ΔT是变量。

由图6可知：当相变结束后，炸药内部与外壁的温差处于最大值，此时对流场的瑞利数也处于最大值，对流传热强度很高，炸药内部的温度迅速趋于均匀。温度趋于均匀后导致ΔT减小，瑞利数也随之减小，对流传热的强度降低，主要传热方式变为热传导；热传导的传热效率低于对流传热，又导致ΔT增大，对流传热强度增大，形成一个循环过程，导致温差曲线出现波动。因此，液态炸药的传热过程并非稳态，传热效率一直在变化，但总体上高于固态炸药的传热效率。

药柱响应阶段开始时，温差曲线出现一个短暂的峰值，再急剧下降直至最终响应。在炸药发生剧烈热分解反应之前，需要吸收热量以使分子达到活化状态，正是这种吸热现象导致响应发生前壁面与中心点的温差出现一个短暂的上升过程。

通过烤燃试验仅能反映出弹体内有限个观测点的温度变化曲线，且实际试验无法观察弹体内各物理场的变化情况，对试验进行数值模拟分析能弥补这一缺陷。

2 数值模拟

熔铸炸药在烤燃过程中需要考虑的物理场主要有重力场、温度场与对流场，流体力学分析软件Fluent能对这些耦合物理场进行联合仿真计算。

2.1 模型建立

参照试验中烤燃弹的实际尺寸建立等比例三维全模型并划分网格，主要网格尺寸为0.5 mm. 完全相变后炸药内部存在流场作用，McClelland等[11]在B炸药的烤燃数值模拟中发现，边界层网格的质量对温度场与流场的计算精度有很大影响，划分网格时应对边界层做加密处理，边界层网格尺寸为0.05～0.20 mm. 网格模型如图7所示。

图7 网格模型Fig.7 Mesh model

在模型中设置2个与试验时炸药内部微型热电偶测点位置相同的温度测点，取OYZ平面(见图7)为研究平面，模型关于Z轴对称。

2.2 参数设置

试验中所用DNAN基熔铸炸药基本物理参数见表1.

表1 试验样本基本物理参数

液态炸药在浮升力作用下形成的自然对流为低速流场，因此对液态炸药采用Boussinesq近似[12]:液态炸药的密度只与温度有关，不考虑其随压强的变化关系，认为流场内的炸药流体为不可压缩流。其数学表达式[13]如下

ρf=ρ0(1-αvΔT)，

(2)

式中：ρf为炸药密度；ρ0为流体的初始密度；αv为热膨胀系数，αv=1.1×10-3.

对于响应之前的整个烤燃过程，假设系统始终不与外界发生物质交换，整个系统内的质量、动量与能量始终守恒，因此可用以下通用表达式表达系统内的任一物理量变化[14]：

(3)

式中：C为质量、动量或能量中的任一物理量；D为C所对应物理量的扩散系数；S为炸药自热反应；μi为速度，xi为特征长度，下角标i为三维矢量方向。

图9 炸药相变过程Fig.9 Phase changing of test sample

炸药自热反应遵循Arrhenius定律，可用以下反应动力学模型[15]来描述：

(4)

式中：Z为炸药指前因子(s-1)；Q为反应热；E为活化能；R为气体常数；T为反应时刻的温度。

使用C语言编写控制外壁升温速率的用户自定义函数(UDF)程序，参照试验设定升温速率为1 K/min，初始温度为20 ℃，根据(3)式编写控制炸药自热反应的UDF程序并嵌入软件。

设置时间步长为5 s，每个时间步内迭代20次，各迭代物理量的松弛因子取默认值。

2.3 仿真结果及分析

仿真中模型内部温度监测点与外壁的温度变化曲线如图8所示。

图8 仿真中各测点温度变化曲线Fig.8 Simulated temperature curves

比较图8与图5可以看出：仿真中各测点的温度变化曲线能很好地与试验中的实际测量曲线相吻合；当温度升至205.8 ℃时，内部测点温度曲线同时出现阶跃，可判定此刻发生了响应。相比图5，图8的误差为0.8%，设置的炸药仿真参数具有较高的可信度。

通过数值仿真观察到药柱在弹体内熔化、沉降的整个相变过程，研究平面的液相分数γ变化如图9所示，每张图间隔时间为1 min. 当γ为0时，单元表现为固相；当γ为1时，单元表现为液相。

相变过程持续了大约8 min，与试验中测得的数据一致。熔化现象首先出现在药柱的上下端边缘，随后发展到整个边界层并向内扩散。相变过程中炸药未熔化部分在重力作用下沉降到壳体底部，在热边界效应作用下形成一个类似倒三角的形状。药柱最后熔化的位置在底部中心附近。

相变前与相变后温度场分布如图10所示。由图10可以看出：相变发生之前，药柱表面温度最高，中心最低，温度最高点位于上下端边缘，最低点位于炸药的几何中心，温度场分布为规则的同心类椭圆形；相变结束之后，温度高的液态炸药在浮升力驱动下向上运动，温度相对较低的炸药在重力作用下向下沉降，二者形成自然对流，导致弹体内部温度分布为上部高、下部低，温度最高点位于上端中心点附近，温度最低点位于底部附近，温度场呈近似层状分布，且相变之后炸药内部的温差较相变之前更小。

图10 烤燃弹内部温度分布云图Fig.10 Distribution of temperature in bomb

图11 响应时刻温度分布云图Fig.11 Distribution of temperature when igniting

响应时刻温度分布云图如图11所示。由图11可以看出，响应时刻点火点在药柱最上端中点处。结合试验中弹体的响应情况分析可知，药柱最上端发生响应以后，弹体内压力急剧升高，上端端盖首先发生剪切破坏，弹体内的高压气体得到释放，降低了点火响应等级。通过大量的数值模拟发现，响应时流场强度不同，响应点在水平方向也会有小幅偏移。

图12是典型非相变炸药黑索今在1 K/min升温速率下的点火位置分布图[16]，药柱尺寸也为φ19 mm×38 mm，点火位置位于药柱的几何中心。图12与图11相比较可以发现，相变炸药与非相变炸药在热刺激下的点火点位置分布有本质的区别。