由一道高三数学模拟题引发的思考
2019-08-05浙江省安吉县高级中学313300
浙江省安吉县高级中学 (313300)
魏侹路
题目(2018年5月某市适应性考试第17题)已知函数f(x)=|x3+ax+b|(a,b∈R),若对任意的x1,x2∈[0,1],f(x1)-f(x2)≤2|x1-x2|恒成立,则a的取值范围是.
1.百花齐放
当x1=x2时该式显然成立,下面重点分析当x1≠x2时的情形.
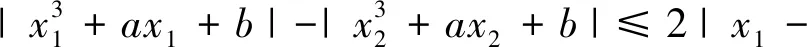
x2|,左边的形式容易联想到绝对值不等式,所以很自然的得出下面的解法1.
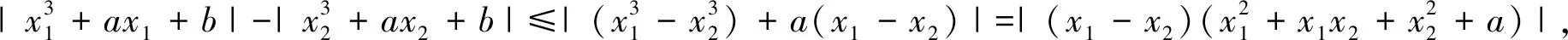
分析2:若将条件f(x1)-f(x2)≤2|x1-x2|中绝对值去掉,当x1
解法2(函数视角):构造函数g1(x)=f(x)+2x,g2(x)=f(x)-2x,根据分析2可知y=g1(x)在[0,1]单调递增,y=g2(x)在[0,1]单调递减,所以-2≤f′(x)≤2.因为f(x)=|x3+ax+b|与g(x)=x3+ax+b的区别仅仅是将图像关于x轴翻折,所以-2≤f′(x)≤2⟺-2≤g′(x)≤2,即-2≤3x2+a≤2在[0,1]上恒成立,可得a∈[-2,-1].

解法3(几何视角):根据分析三可知,只需要f(x)图像上任意两点连线的斜率k∈[-2,2]即可.因为当两点无限靠近时,割线的斜率可转化为切线的斜率,所以只需要-2≤f′(x)≤2即可,下同解法2.
2.陷入疑惑
在上述三种解法中不难发现有两个问题值得我们思考:第一,一个函数关于x轴翻折前后导数的取值范围之间存在何种联系?是不是给范围加上个绝对值这么简单?第二,一个函数割线斜率的取值范围,是不是等于切线斜率的取值范围?如果能解决第二个问题,第一个问题类似的从图形上来解释应该成立.所以,接下来要研究的就是第二个问题.
我们先来看一个比较熟悉的函数y=x3,如果记集合A,B分别是割线斜率和切线斜率取值的集合.从图像观察可知A=(0,+∞),而通过求导可知y′=3x2,故B=[0,+∞),显然A≠B,直接否定猜想.
3.拨开云雾
其实,割线斜率与切线斜率间的关系问题,具有高等数学背景,这就是拉格朗日中值定理:
若函数y=f(x)是[a,b]上的连续函数,且在(a,b)上可导,则∃ξ∈(a,b)使得f′(ξ)=
从这个定理说明割线斜率取值的集合M一定是切线斜率取值的集合N的子集,那么有没有可能A=B呢?我们注意到,刚才列举的反例中,之所以A≠B问题在于集合B中多取了一个元素0,这是x=0处切线的斜率,而x=0刚好是函数y=x3的拐点.如果函数不存在拐点,是不是就有A=B了呢?
结论1设y=f(x)是定义在(a,b)上的二阶可导函数,其对应曲线C上任意两点连线(割线)斜率取值的集合记为A,曲线C上任意一点处切线斜率取值的集合记为B.若函数y=f(x)在(a,b)是凹函数或凸函数,则A=B.

图1
证明:根据拉格朗日中值定理显然A⊆B,下面只需要证明B⊆A即可.对于∀k∈B,即∃x0使得f′(x0)=k,因为y=f(x)在(a,b)是凹函数或凸函数,故函数图像始终在x=x0的同侧.只要将切线l向上或向下平移即可得到斜率为k的割线m.如图1.
由此我们可以看出,若函数y=f(x)在(a,b)上不存在拐点时,A=B是成立的.那么,当存在一个拐点时,集合A,B之间的关系又如何呢?
结论2设y=f(x)是定义在(a,b)上的二阶可导函数,其对应曲线C上任意两点连线(割线)斜率取值的集合记为A,曲线C上任意一点处切线斜率取值的集合记为B.若函数y=f(x)在(a,b)内存在唯一的拐点x=x0,则CBA={f′(x0)}.
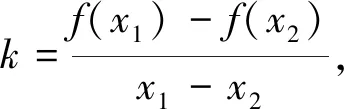
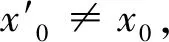
有了这两个结论,我们再来思考刚才的解法3.我们知道,g(x)=x3+ax+b作为三次函数有且仅有唯一的拐点,所以g′(x)=3x2+a∈[a,a+3],这个范围比斜率k的范围仅多出了g′(0)=a一个值,故斜率k的范围是(a,a+3]⊆[-2,2]⟹a∈[-2,-1].
4.高屋建瓴
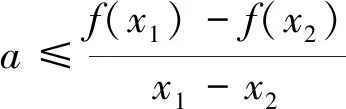
例1 (2010辽宁理数21)已知函数f(x)=(a+1)lnx+ax2+1.
(1)讨论函数f(x)的单调性;
(2)设a<-1,如果对任意x1,x1∈(0,+∞),f(x1)-f(x2)≥4|x1-x2|,求a的取值范围.
解:(1)略;(2)当x1=x2时该式显然成立,下面重点分析当x1≠x2时的情形:f(x1)-f(x2)≥


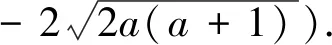

特别的,∃ξ∈(b,x)使得f′(ξ)=


例2 (2017全国Ⅱ文数21)设函数f(x)=(1-x2)ex.
(1)讨论f(x)的单调性;
(2)当x≥0时,f(x)≤ax+1,求a的取值范围.
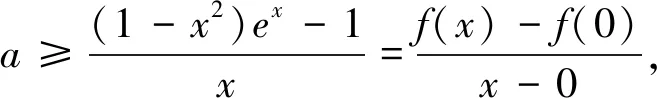
这两种类型的问题还是比较多的,限于篇幅的原因,在此不再赘述.
五、再入迷途
正当笔者为找到高观点下的“秒杀”解法而欣喜不已时,下面遇到的这个问题却给了笔者当头一棒.
例3 (2012全国理数20)设函数f(x)=ax+cosx,x∈[0,π].
(1)讨论f(x)的单调性;
(2)设f(x)≤1+sinx,求a的取值范围.
在思考第(2)问时,本人采取了类似例2的解法:

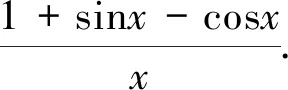
6.柳暗花明
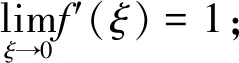


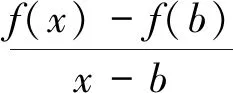
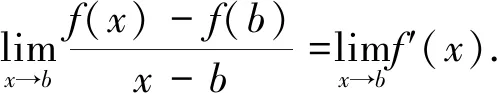
7.蓦然回首
回顾本题一路走来的过程,可谓一波三折,从疑惑到释惑,再到疑惑,再释惑.可能这种解法本身对于普通学生来说涉及到了高等数学的背景,难度过大,未必适合介绍.但是对于优秀的学生来说,未尝不是眼界的开阔,以便于他们今后能站在一个更高的层次思考问题.当然,经历这个过程以后,本人感觉更重要的并不是得出了什么结论,而是在于今后的教学过程中,如何让学生经历收获知识的过程.
首先,应该坚持以问题为导向.就连爱因斯坦也认为,提出一个问题比解决一个问题更重要.比起直接教授学生这样那样的“秒杀”技巧,如何引导学生发现问题以及思考下去更值得我们思考.当然,研究的问题应该是符合学生认知水平,并适合提优拔高的问题.
其次,应该注意问题之间的内在逻辑关系,合理展示问题的发展过程.许多问题的提出并不是一蹴而就的,就像许多结论的得出往往也不能一步到位.对于复杂问题,如何合理设置问题链,帮助学生习得数学的思维方式,掌握解决问题的数学思想才是更重要的.
最后,对于一道数学题目进行横向纵向的挖掘,对学生数学思维的开发是极有帮助的一件事情,怎样做的更科学更合理是值得我们每位教师不断去研究的课题.
