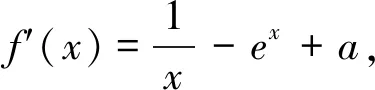百转千回妙用隐零点
2019-08-05江苏省盱眙中学211700
江苏省盱眙中学 (211700)
梁 义
函数零点是新课标教材中的新增内容之一,纵观近几年各地模拟试题,经常出现一些与零点有关的问题,它可以以填空题的形式出现,也可以在解答题中与其他知识交汇考查,可以说“零点”已经成为了新的热点、亮点和思维生长点.特别是有些零点不是显性给出时,我们称之为“隐零点”(既能确定其存在,又无法用显性的代数式进行表达),这时就需要根据相关知识进行转化,本文通过范例归纳出隐藏零点的转化方法.
引例(2019届高三徐州期中)已知函数f(x)=x|x2-a|-a,若f(x)有三个零点,则实数a的取值范围是.
解析:(1)a=0时,f(x)=x|x2|=x3,只有一个零点,不合题意.
(2)a<0时,f(x)=x(x2-a)-a=x3-ax-a,f′(x)=3x2-a>0,f(x)在R上单调递增,所以,f(x)=x3-ax-a=0不可能有3个解,也不合题意.
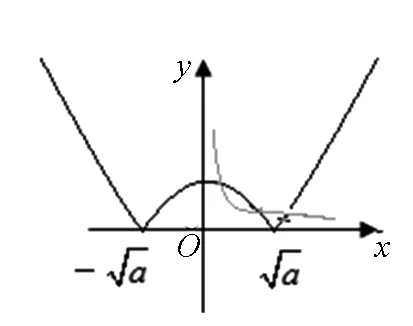
图1
(3)a>0时,f(x)=
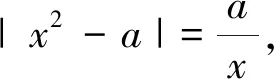
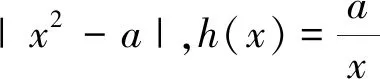
评注:本题解决函数零点个数问题时,通过对问题的转化:函数零点⟺方程的根⟺方程组的解(两个函数图像的交点),进而实现了问题解决.
从引例可以看出,解决该类型问题时往往需要灵活、合理的转化,下面以近年各地的试题为例说明这部分内容的常见题型及求解策略,以期对各位读者有所启示.
一、显隐混搭,图像相助
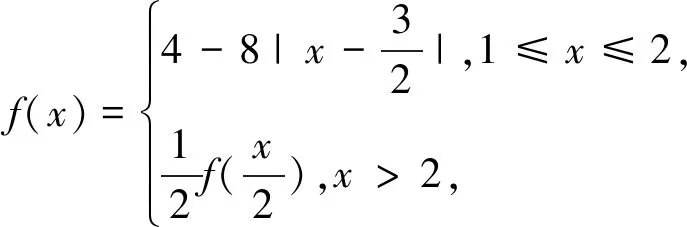
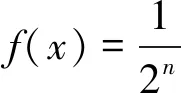
评注:此类函数给出了某一部分区间内的表达式背景新颖、构思巧妙,将显、隐函数完美的结合.解决这类问题时,可以通过函数与方程形式的转化,结合图像变换(平移、伸缩、翻折等),让图像成为解决问题的一把利器.
二、虚设零点,整体代换
例2 已知函数f(x)=ax2-x-lnx,a∈R.
(1)若-1≤a≤0,证明:函数f(x)有且只有一个零点;
(2)若函数f(x)有两个零点,求实数a的取值范围.
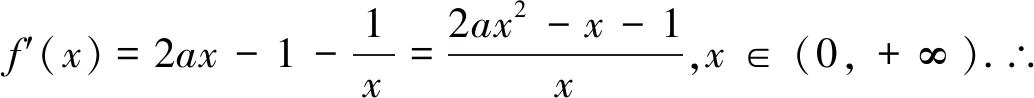
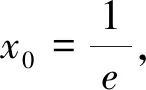
综上,当-1≤a≤0时,函数f(x)在(0,+∞)有且只有一个零点.
(另:可以考虑放缩,利用lnx≤x-1,则f(x)≥ax2-2x+1,则必然存在x0∈(0,1),使得f(x)>0)
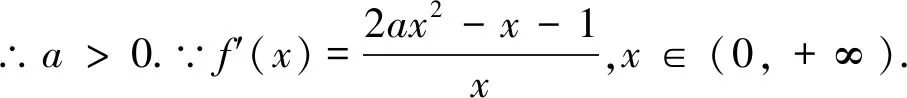
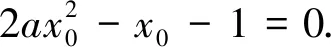
当x∈(0,x0)时,g(x)<0,f′(x)<0;当x∈(x0,+∞)时,g(x)>0,f′(x)>0.∴函数f(x)在(0,x0)上单调递减;在(x0,+∞)上单调递增.
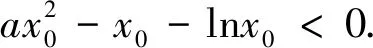
以下验证:当0 例3 已知函数f(x)=lnx-ex+ax-a,若关于x的方程f(x)=0有唯一解x0,且x0∈(n,n+1),n∈N*,求n的值. N*知n=1. 点评:对于此类问题的处理,一般没有现成的规律和方法可循.我们只能通过一些手段去探求问题的正确思路.比如:①化归,尝试着将问题转化为一个我们较为熟悉的问题或者是另外一种表达方式,看看是否有益寻找正确的思路;②结合已知的表达式,看清影响函数取值的主要因素,合理有效地去猜测、验证,调整,再验证,必要的话,不断重复这样的过程;③结合常见的不等式去放缩,看看是否对解题有帮助.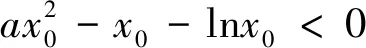
三、数值估算,步步为营