厘清教材脉络 探明解题思路——平面向量最值问题的解决途径

☉安徽省淮南市教育体育局中小学教研室 苏里阳

平面向量兼具“数”和“形”的特点，是沟通代数、几何与三角函数的有力工具，作为高考必考内容之一备受命题者的青睐，考题一般具有小巧灵活的特点，解法多样，且魅力独特.纵览该部分内容，几何中的全等、相似、平行、垂直等关系在向量的概念引入后就可以转化为向量的加（减）法、数乘向量、数量积等运算，从而把图形的基本性质转化为向量的运算体系，因此向量的线性运算具有深刻的几何意义.平面向量基本定理是平面向量正交分解及坐标表示的基础，向量的坐标运算实际上是向量的代数表示，引入向量的坐标表示可使向量运算完全代数化，这就可以使很多几何问题的解答转化为学生所熟悉的代数运算.向量的数量积把向量的长度和三角函数联系起来，利用向量数量积可以解决夹角、模长、距离等问题.下面从“数”和“形”两个角度，分别谈谈平面向量的最值问题的解决途径.

一、从“形”的视角

1.图形法

图形法是指结合向量的几何意义并利用图形表示来解决问题的方法.向量的运算引入后，其工具性作用才能得到充分的发挥，在引进一种向量运算后，总是要考查一下它的几何意义，向量的线性运算的几何意义主要是结合平行四边形和三角形来讲述的.正因为向量运算的几何意义，才使得向量在解决几何问题时可以发挥很好的作用.

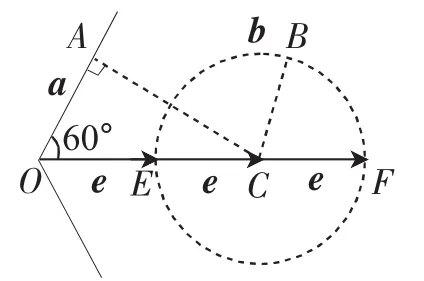
图1

例1（2018年浙江高考第9题） 已知a，b，e是平面向量，e是单位向量.若非零向量a与e的夹角为，向量b满足b2-4e·b+3=0，则|a-b|的最小值是（ ）.

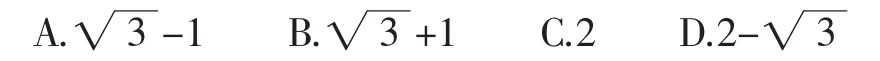
解法1：由b2-4e·b+3=0，得（b-e）·（b-3e）=0.设b=.所以=0.取EF的中点为C，则B在以C为圆心，EF为直径的圆上，如图1，设a=作射线OA，使得，则|a-b|=（|a-2e）.故选A.

解法2：因为b2-4e·b+3=0，所以（b-2e）2=1，|b-2e|=1.把a，b，e的起点作为公共点O，则b的终点在以点C为圆心，半径为1的圆上，|a-b|就是线段AB的长度.要求|AB|的最小值即求圆上动点B到定直线OA的距离的最小值，也就是圆心C到直线OA的距离减去圆的半径，因此|a-b|的最小值为1.

本题乍一看让人无从下手，仔细揣摩题干中的条件b2-4e·b+3=0，可以转化为两向量垂直或向量模长为1，然后利用图形，则其数量关系、位置关系在图形中一目了然，从而使问题能够快速且准确地得到解决.

2.基底法

基底法是指利用平面向量的基本定理和向量的线性运算来解决问题的方法，根据题设条件选择两个模长和夹角已知或易求的不共线的向量作为基底，将所求向量用此基底表示出来，从而把问题转化为关于已知向量的计算问题.

例2设平面向量α，β满足|α+2β|=3，|2α+3β|=4，则α·β的最小值为______.

破解本题的关键在于根据向量α+2β和2α+3β的模长已知，选择=α+2β与=2α+3β作为基底，利用平面向量的线性运算表示出α，β，进而借助向量的数量积的定义式来进行求解.

二、从“数”的视角

1.坐标法

坐标法是建立适当的直角坐标系，将已知条件和所求问题用坐标表示出来，然后将向量问题完全代数化，进而解决问题的方法.向量问题中如果含有具有垂直关系的图形，或者是考查函数以及与解析几何相关的问题都可以考虑用坐标法.

例3（2018年天津高考理科第8题）如图2，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BAD=120°，AB=AD=1，若点E为边CD上的动点，则A■→E·B■→E的最小值为（ ）.

图2

图3

解：由四边形的特殊性，分别以DA，DC所在的直线为x轴、y轴建立如图3的直角坐标系，则A（1，0），），D（0，0），又点E在边CD上，设 E（0，t），且 t∈［0，］，故=（-1，t），=），所以又因为t∈］，所以当时有最小值故选A.

2.数量化

数量化是指已知向量关系式，要求代数式的最值，可以利用数量积运算将向量等式转化为数量等式，找出变量之间的联系，进而破解最值问题.

例4平行四边形ABCD中，AB=3，AD=2，∠BAD=120°，P是平行四边形ABCD内一点，且AP=1，若，则3x+2y的最大值为______.

三、数与形结合，解题更省力

例5 已知向量a，b满足|a|=1，且对任意实数x，y，|axb|的最小值为，|b-ya|的最小值为，则|a+b|=（ ）.

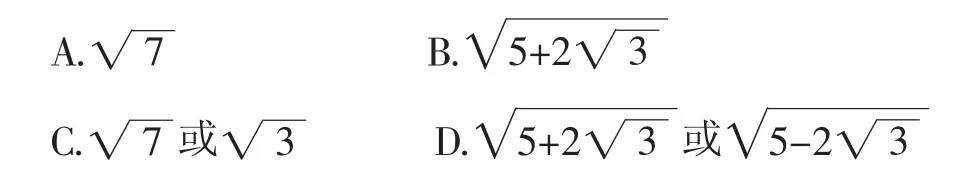
解法1：设a=（1，0），b=（m，n），

因为|a-xb|2=（1-xm）2+（-xn）2=（m2+n2）x2-2mx+1，且对任意的x∈R有|a-xb|的最小值为，所以可得，化简得n2=3m2.同理由|b-ya|的最小值为，得m=±1，所以n2=3.故|a+b|2=（1+m）2+n2=7或3.故答案选C.

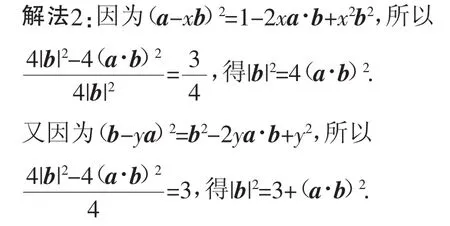
所以a·b=1或-1，所以|a+b|2=a2+b2+2ab=7或3，故|a+b|=或.故选C.

平面向量有关最值问题的解题途径实际上都源于基本的转化与化归思想，在平时学习中应予以重视.从整体上把握教材的知识脉络，通过图形法、基底法、坐标法、数量化等策略可以有效应对此类题型.只要我们能重视考查知识的来龙去脉，遵循解题的基本规律，抓住平面向量的本质——沟通代数与几何的桥梁，认真分析已知和所求之间的联系，多角度地去解读，并进行对比、分析，反复琢磨，积累更多的经验就能做到举一反三、触类旁通.W